2.1 认识有理数 教学设计(表格式) 北师大版数学七年级上册
文档属性
| 名称 | 2.1 认识有理数 教学设计(表格式) 北师大版数学七年级上册 |
|
|
| 格式 | doc | ||
| 文件大小 | 823.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 00:00:00 | ||
图片预览



文档简介
2.1 认识有理数
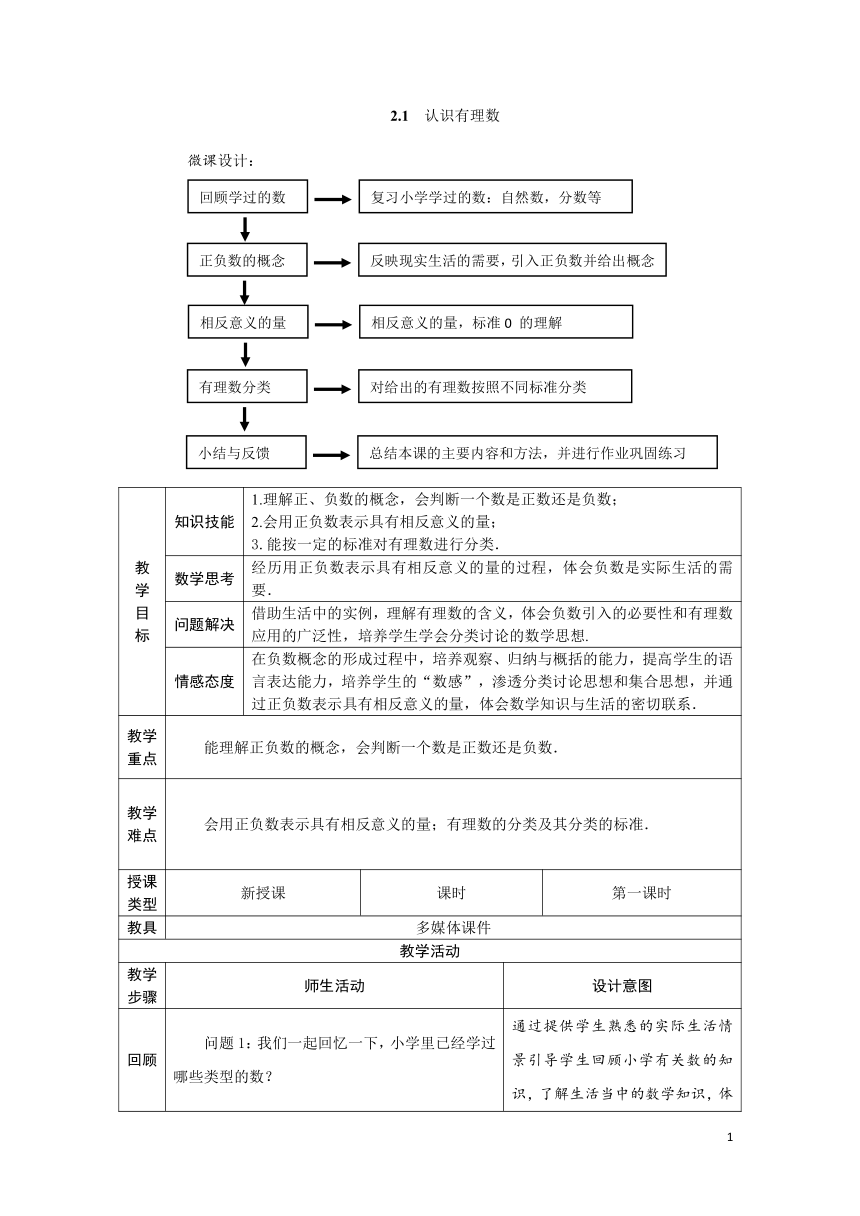
微课设计:
教学目标 知识技能 1.理解正、负数的概念,会判断一个数是正数还是负数;2.会用正负数表示具有相反意义的量;3.能按一定的标准对有理数进行分类.
数学思考 经历用正负数表示具有相反意义的量的过程,体会负数是实际生活的需要.
问题解决 借助生活中的实例,理解有理数的含义,体会负数引入的必要性和有理数应用的广泛性,培养学生学会分类讨论的数学思想.
情感态度 在负数概念的形成过程中,培养观察、归纳与概括的能力,提高学生的语言表达能力,培养学生的“数感”,渗透分类讨论思想和集合思想,并通过正负数表示具有相反意义的量,体会数学知识与生活的密切联系.
教学重点 能理解正负数的概念,会判断一个数是正数还是负数.
教学难点 会用正负数表示具有相反意义的量;有理数的分类及其分类的标准.
授课类型 新授课 课时 第一课时
教具 多媒体课件
教学活动
教学步骤 师生活动 设计意图
回顾 问题1:我们一起回忆一下,小学里已经学过哪些类型的数?学生回答后,教师以数的发展史在PPT上呈现数的发展史,它们都是由于实际需要而产生的.设计意图:让学生体验数的发展历史,体现古人在研究数学上所付出的努力和数的发展真实性.为后续负数发展史的作铺垫,即负数的出现和生活息息相关。 通过提供学生熟悉的实际生活情景引导学生回顾小学有关数的知识,了解生活当中的数学知识,体会“数”的实际意义,理解数学与生活息息相关.
(续表)
活动一:创设情境导入新课 你能用小学学过的数表示下列数吗?图2-1-处理方式:让学生发现出现了新的需要表示的数,从而引入具有相反意义的量,继而引入本节课内容. 结合已有的知识经验,和生活常识,通过问题的形式引导学生发现“新数”进而引入课题.让学生发现生活中到处存在数学知识,提高学生学习的兴趣.
活动二:实践探究交流新知 旧知再认:正负数概念 问题1:某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不 回答得0分;每个队的基本分均为0分.两个队答题情况如下表:答题情况第一队第二队如果答对题所得的分数用正数表示,那么你能写出每个队答题得分的情况吗?试完成下表:答对题的得分答错题的得分未回答题的得分第一队+6第二队-2处理方式:学生自主思考得出结论.像+5,+1.2, ,6等大于零的数,叫做正数。它们都比零大。 像-5,-1.2, ,-6 等在正数前面加上“-”号的数叫做负数,它们都比零小。“0”既不是正数,也不是负数。 零除了表示没有,还是正负数的分界,是基准。 问题2:生活中你见过其他用负数表示的量吗?请你说一说。表中的3.3表示2010年全国居民消费价格比三年上涨3.3%;请你说一说0.0,-0.6分别表示什么意思?处理方式:让学生用同样的方法表示出前面例子中具有相反意义的量.教师引导学生认识0的位置.具有相反意义的量阅读教材24页第一自然段和25页《负数小史》,思考下面的问题,(1)为什么要引入负数?负数怎么表示的?(2)小明月考数学成绩进步5分和退步5分,如果都记作:5分,那么你能分清小明是进步了5分还是退步了5分吗?用什么表示方法可以明显将区分开来呢?具有相反意义的量:上升与下降、增与减、收入与支出、胜与负、进与退、多与少、盈利与亏损东与西、顺与逆、过剩与不足、重与轻等.正数和负数可以表示具有相反意义的量。设计意图:引导学生学会阅读课本,并总结出负数出现的生活必要性,理解正数和负数可以表示具有相反意义的量。 用趣味情景启发学生用正负数表示相反意义的量,初步让学生认识负数,知道负数的来源与生活的需要.通过对实例的分析,让学生知道如何用正负数表示相反意义的量.
(续表)
活动二:实践探究交流新知 例1 (1)某人转动转盘,如果用+5圈表示沿逆时针方向转了 5圈,那么沿顺时针方向转了 12圈怎样表示? (2)在某次乒乓球质量检测中,一只乒乓球超出 标准质量0.02 g记作+0.02 g,那么- 0.03 g表示什么? (3)某大米包装袋上标注着“净含量:10 kg ± 150 g”,这里的 “10 kg ±150 g”表示什么?(4)如果乒乓球高于标准质量比较多会怎样呢?如果你买到的大米少了100克,会做出什么选择?如果买到的大米多了300克,你又会做出什么选择?
处理方式:先让学生自己独立完成,加深学生对正负数的理解;同时渗透遵守规则等德育教育.探究活动2:你能选定一个重量为标准,用正负数表示下面八位同学的体重与选定的体重标准的差异吗?你是怎样表示的?52, 51.5, 49.5, 50.5, 45, 56, 47.5, 42.5问题::A:52用+2表示的;B:52用+3表示的。你知道为什么会这样吗?处理方式:学独立思考自己的答案以及理由,教师引导学生发现其中的差异,分析找出存在差异的原因是标准不同.探究活动3:有理数的概念及分类 请你把我们所学过的数进行分类 1.新的整数、分数概念:引进负数后,数的范围扩大了.过去我们说整数只包括正整数和零,引进负数后,正整数前加上负号的数叫做负整数,因而整数包括正整数、负整数和零,同样分数包括正分数、负分数.整数和分数统称为有理数.2.有理数的分类问题:为了便于研究某些问题,常常需要将有理数进行分类,需要不同,分类的方法也常常不同,根据有理数的定义可将有理数分成两类:整数和分数.有理数还有没有其他的分类方法? 通过巩固练习加深对具有相反意义的量表示,进一步加强对负数的理解与应用.通过思考让学生进一步认识负数,并了解0的意义及作用.学生在原有认知结构的基础上,将数扩充到了有理数的范围.通过练习使学生加深理解有理数的意义.
(续表)
活动二:实践探究交流新知 归纳总结:按有理数的符号分为三类:正有理数、负有理数和零,并向学生强调:分类可以根据不同需要,用不同的分类标准,但必须对讨论对象不重不漏地分类.教材拓展1.把________数和________统称为非负整数(也叫自然数),把______数和______统称为非正整数.
活动三:开放训练体现应用 【应用举例】例1 把下列各数分别填入相应的大括号内: 正数集合 { …};整数集合 { …};负分数集合 { …};非负整数集合{ …};有理数集合 { …}; 通过例题进一步理解有理数的分类。
活动四:课堂总结反思 本节微课你收获哪些知识和数学方法?【当堂检测】1.-3.782( )A.是负数,不是分数 B.不是分数,是有理数C.是负数,也是分数 D.是分数,不是有理数2.下面说法中正确的是( )A.正整数和负整数统称为整数B.分数不包括整数C.正分数,负分数,负整数统称有理数D.正整数和正分数统称正有理数3.一种零件的长度在图纸上是(10±0.05)毫米,表示这种零件的标准尺寸是10毫米,加工要求最大不超过________毫米,最小不小于________毫米. 通过练习发现学生的本节课知识掌握情况,总结本节课的教学效果,并为课下辅导做好准备.
(续表)
复习小学学过的数:自然数,分数等
回顾学过的数
反映现实生活的需要,引入正负数并给出概念
正负数的概念
相反意义的量,标准0 的理解
相反意义的量
有理数分类
对给出的有理数按照不同标准分类
总结本课的主要内容和方法,并进行作业巩固练习
小结与反馈
PAGE
5
微课设计:
教学目标 知识技能 1.理解正、负数的概念,会判断一个数是正数还是负数;2.会用正负数表示具有相反意义的量;3.能按一定的标准对有理数进行分类.
数学思考 经历用正负数表示具有相反意义的量的过程,体会负数是实际生活的需要.
问题解决 借助生活中的实例,理解有理数的含义,体会负数引入的必要性和有理数应用的广泛性,培养学生学会分类讨论的数学思想.
情感态度 在负数概念的形成过程中,培养观察、归纳与概括的能力,提高学生的语言表达能力,培养学生的“数感”,渗透分类讨论思想和集合思想,并通过正负数表示具有相反意义的量,体会数学知识与生活的密切联系.
教学重点 能理解正负数的概念,会判断一个数是正数还是负数.
教学难点 会用正负数表示具有相反意义的量;有理数的分类及其分类的标准.
授课类型 新授课 课时 第一课时
教具 多媒体课件
教学活动
教学步骤 师生活动 设计意图
回顾 问题1:我们一起回忆一下,小学里已经学过哪些类型的数?学生回答后,教师以数的发展史在PPT上呈现数的发展史,它们都是由于实际需要而产生的.设计意图:让学生体验数的发展历史,体现古人在研究数学上所付出的努力和数的发展真实性.为后续负数发展史的作铺垫,即负数的出现和生活息息相关。 通过提供学生熟悉的实际生活情景引导学生回顾小学有关数的知识,了解生活当中的数学知识,体会“数”的实际意义,理解数学与生活息息相关.
(续表)
活动一:创设情境导入新课 你能用小学学过的数表示下列数吗?图2-1-处理方式:让学生发现出现了新的需要表示的数,从而引入具有相反意义的量,继而引入本节课内容. 结合已有的知识经验,和生活常识,通过问题的形式引导学生发现“新数”进而引入课题.让学生发现生活中到处存在数学知识,提高学生学习的兴趣.
活动二:实践探究交流新知 旧知再认:正负数概念 问题1:某班举行知识竞赛,评分标准是:答对一题加1分,答错一题扣1分,不 回答得0分;每个队的基本分均为0分.两个队答题情况如下表:答题情况第一队第二队如果答对题所得的分数用正数表示,那么你能写出每个队答题得分的情况吗?试完成下表:答对题的得分答错题的得分未回答题的得分第一队+6第二队-2处理方式:学生自主思考得出结论.像+5,+1.2, ,6等大于零的数,叫做正数。它们都比零大。 像-5,-1.2, ,-6 等在正数前面加上“-”号的数叫做负数,它们都比零小。“0”既不是正数,也不是负数。 零除了表示没有,还是正负数的分界,是基准。 问题2:生活中你见过其他用负数表示的量吗?请你说一说。表中的3.3表示2010年全国居民消费价格比三年上涨3.3%;请你说一说0.0,-0.6分别表示什么意思?处理方式:让学生用同样的方法表示出前面例子中具有相反意义的量.教师引导学生认识0的位置.具有相反意义的量阅读教材24页第一自然段和25页《负数小史》,思考下面的问题,(1)为什么要引入负数?负数怎么表示的?(2)小明月考数学成绩进步5分和退步5分,如果都记作:5分,那么你能分清小明是进步了5分还是退步了5分吗?用什么表示方法可以明显将区分开来呢?具有相反意义的量:上升与下降、增与减、收入与支出、胜与负、进与退、多与少、盈利与亏损东与西、顺与逆、过剩与不足、重与轻等.正数和负数可以表示具有相反意义的量。设计意图:引导学生学会阅读课本,并总结出负数出现的生活必要性,理解正数和负数可以表示具有相反意义的量。 用趣味情景启发学生用正负数表示相反意义的量,初步让学生认识负数,知道负数的来源与生活的需要.通过对实例的分析,让学生知道如何用正负数表示相反意义的量.
(续表)
活动二:实践探究交流新知 例1 (1)某人转动转盘,如果用+5圈表示沿逆时针方向转了 5圈,那么沿顺时针方向转了 12圈怎样表示? (2)在某次乒乓球质量检测中,一只乒乓球超出 标准质量0.02 g记作+0.02 g,那么- 0.03 g表示什么? (3)某大米包装袋上标注着“净含量:10 kg ± 150 g”,这里的 “10 kg ±150 g”表示什么?(4)如果乒乓球高于标准质量比较多会怎样呢?如果你买到的大米少了100克,会做出什么选择?如果买到的大米多了300克,你又会做出什么选择?
处理方式:先让学生自己独立完成,加深学生对正负数的理解;同时渗透遵守规则等德育教育.探究活动2:你能选定一个重量为标准,用正负数表示下面八位同学的体重与选定的体重标准的差异吗?你是怎样表示的?52, 51.5, 49.5, 50.5, 45, 56, 47.5, 42.5问题::A:52用+2表示的;B:52用+3表示的。你知道为什么会这样吗?处理方式:学独立思考自己的答案以及理由,教师引导学生发现其中的差异,分析找出存在差异的原因是标准不同.探究活动3:有理数的概念及分类 请你把我们所学过的数进行分类 1.新的整数、分数概念:引进负数后,数的范围扩大了.过去我们说整数只包括正整数和零,引进负数后,正整数前加上负号的数叫做负整数,因而整数包括正整数、负整数和零,同样分数包括正分数、负分数.整数和分数统称为有理数.2.有理数的分类问题:为了便于研究某些问题,常常需要将有理数进行分类,需要不同,分类的方法也常常不同,根据有理数的定义可将有理数分成两类:整数和分数.有理数还有没有其他的分类方法? 通过巩固练习加深对具有相反意义的量表示,进一步加强对负数的理解与应用.通过思考让学生进一步认识负数,并了解0的意义及作用.学生在原有认知结构的基础上,将数扩充到了有理数的范围.通过练习使学生加深理解有理数的意义.
(续表)
活动二:实践探究交流新知 归纳总结:按有理数的符号分为三类:正有理数、负有理数和零,并向学生强调:分类可以根据不同需要,用不同的分类标准,但必须对讨论对象不重不漏地分类.教材拓展1.把________数和________统称为非负整数(也叫自然数),把______数和______统称为非正整数.
活动三:开放训练体现应用 【应用举例】例1 把下列各数分别填入相应的大括号内: 正数集合 { …};整数集合 { …};负分数集合 { …};非负整数集合{ …};有理数集合 { …}; 通过例题进一步理解有理数的分类。
活动四:课堂总结反思 本节微课你收获哪些知识和数学方法?【当堂检测】1.-3.782( )A.是负数,不是分数 B.不是分数,是有理数C.是负数,也是分数 D.是分数,不是有理数2.下面说法中正确的是( )A.正整数和负整数统称为整数B.分数不包括整数C.正分数,负分数,负整数统称有理数D.正整数和正分数统称正有理数3.一种零件的长度在图纸上是(10±0.05)毫米,表示这种零件的标准尺寸是10毫米,加工要求最大不超过________毫米,最小不小于________毫米. 通过练习发现学生的本节课知识掌握情况,总结本节课的教学效果,并为课下辅导做好准备.
(续表)
复习小学学过的数:自然数,分数等
回顾学过的数
反映现实生活的需要,引入正负数并给出概念
正负数的概念
相反意义的量,标准0 的理解
相反意义的量
有理数分类
对给出的有理数按照不同标准分类
总结本课的主要内容和方法,并进行作业巩固练习
小结与反馈
PAGE
5
同课章节目录
