华师大版八年级数学下册课件:19.1矩形的性质(共20张PPT)
文档属性
| 名称 | 华师大版八年级数学下册课件:19.1矩形的性质(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 253.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-04 00:00:00 | ||
图片预览






文档简介
课件19张PPT。 矩形的性质
19.1矩形第19章 矩形、菱形与正方形学习目标:
1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
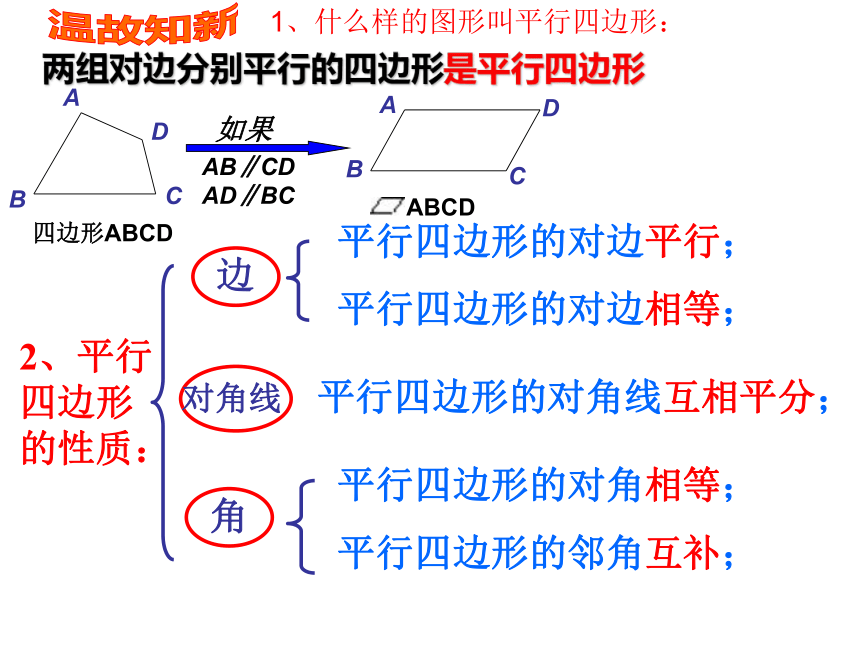
2.会初步运用矩形的概念和性质来解决有关问题.两组对边分别平行的四边形是平行四边形2、平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分; 温故知新1、什么样的图形叫平行四边形:创设情景我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说也有特殊的平行四边形,这堂课我们就来研究一种特殊的平行四边形—— 矩形看到这个课题你想知道什么?设疑自探自探提示:自学课本98---99页内容,思考:
1、什么叫矩形?它和平行四边形有什么关系?
2、观察课本98页图19.1.2,完成课本99页表格。
3、矩形有什么性质?第五节矩形菱形有一个角是直角的平行四边形叫做矩形。矩形的定义:解疑合探矩形的性质的研究:我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?四、矩形 两条对角线互相平分三、矩形的两组对角分别相等二、矩形的两组对边分别相等一、矩形的两组对边分别平行五、矩形的邻角互补矩形的特殊性质:
矩形的性质定理1 矩形的四个角都是直角。
矩形的性质定理2 矩形的对角线相等。
你会证明这两个定理吗?定理1:矩形的四个角都是直角;已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°证明:∵矩形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形
求证:AC = BD证明:∵四边形ABCD是矩形∴∠ABC = ∠DCB = 90° AB = DC ,
又∵BC = CB∴△ABC≌△DCB(SAS)∴AC = BD定理2:矩形的对角线相等;边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且平分;思考:矩形ABCD是轴对称图形吗?它的对称轴有几条?矩形是中心对称图形吗?对称中心是?ABCDEFGH.质疑再探:ODCBA1、已知矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形周长和是86cm,矩形的对角线长是13cm,那么该矩形的周长是多少?运用拓展:ODCBA相等的线段:相等的角:∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB2、已知四边形ABCD是矩形3、 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:∵四边形ABCD是矩形
∴ OA=OB
∵∠AOB=60° ∴△AOB是等边三角形
∴OA=AB=4(㎝)
∴矩形的对角线长 AC=BD=2OA=8(㎝)有一个角是直角的
平行四边形叫矩形2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分 且相等1.矩形的定义:3.矩形是轴对称图形,也是中心对称图形.课堂小结本节课你有什么收获?学科班长总结!作业:
课本100页练习2、3题
再 见
19.1矩形第19章 矩形、菱形与正方形学习目标:
1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
2.会初步运用矩形的概念和性质来解决有关问题.两组对边分别平行的四边形是平行四边形2、平行四边形的性质:平行四边形的对边平行;平行四边形的对边相等;平行四边形的对角相等;平行四边形的邻角互补;平行四边形的对角线互相平分; 温故知新1、什么样的图形叫平行四边形:创设情景我们已经知道平行四边形是特殊的四边形,因此平行四边形除具有四边形的性质外,还有它的特殊性质,同样对于平行四边形来说也有特殊的平行四边形,这堂课我们就来研究一种特殊的平行四边形—— 矩形看到这个课题你想知道什么?设疑自探自探提示:自学课本98---99页内容,思考:
1、什么叫矩形?它和平行四边形有什么关系?
2、观察课本98页图19.1.2,完成课本99页表格。
3、矩形有什么性质?第五节矩形菱形有一个角是直角的平行四边形叫做矩形。矩形的定义:解疑合探矩形的性质的研究:我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?四、矩形 两条对角线互相平分三、矩形的两组对角分别相等二、矩形的两组对边分别相等一、矩形的两组对边分别平行五、矩形的邻角互补矩形的特殊性质:
矩形的性质定理1 矩形的四个角都是直角。
矩形的性质定理2 矩形的对角线相等。
你会证明这两个定理吗?定理1:矩形的四个角都是直角;已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°证明:∵矩形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°已知:四边形ABCD是矩形
求证:AC = BD证明:∵四边形ABCD是矩形∴∠ABC = ∠DCB = 90° AB = DC ,
又∵BC = CB∴△ABC≌△DCB(SAS)∴AC = BD定理2:矩形的对角线相等;边对角线角矩形的性质:矩形对边平行且相等;矩形的四个角都是直角;矩形的对角线相等且平分;思考:矩形ABCD是轴对称图形吗?它的对称轴有几条?矩形是中心对称图形吗?对称中心是?ABCDEFGH.质疑再探:ODCBA1、已知矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形周长和是86cm,矩形的对角线长是13cm,那么该矩形的周长是多少?运用拓展:ODCBA相等的线段:相等的角:∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB2、已知四边形ABCD是矩形3、 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长? 解:∵四边形ABCD是矩形
∴ OA=OB
∵∠AOB=60° ∴△AOB是等边三角形
∴OA=AB=4(㎝)
∴矩形的对角线长 AC=BD=2OA=8(㎝)有一个角是直角的
平行四边形叫矩形2.矩形的性质:对边平行且相等四个角都是直角对角线互相平分 且相等1.矩形的定义:3.矩形是轴对称图形,也是中心对称图形.课堂小结本节课你有什么收获?学科班长总结!作业:
课本100页练习2、3题
再 见
