2025年中考数学九年级一轮复习【函数】专题(一次函数部分)过关题(含答案)
文档属性
| 名称 | 2025年中考数学九年级一轮复习【函数】专题(一次函数部分)过关题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 351.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年中考数学九年级
一轮复习【函数】专题(一次函数部分)过关题
一、单选题
1.(2019·三亚模拟)一次函数y=﹣2x+5不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2024·泰安模拟)函数的图象如图所示,则关于x的一元二次方程的根的情况是( )
A.没有实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.无法确定
3.(2022八下·大足期中)若一次函数y=(k-3)x-1的图像不经过第一象限,则( )
A.k<3 B.k>3 C.k>0 D.k<0
4.(2024八下·阳高期末)如图是1个纸杯和6个纸杯叠放在一起的示意图.小红想探究叠放在一起的杯子的总高度随杯子数量的变化关系.她将50个同样的纸杯叠放在一起,则这50个纸杯的总高度约为( )
A. B. C. D.
5.(2024九下·高邮模拟)下列关于函数的图象与性质叙述错误的是( )
A.该函数图象关于直线对称 B.该函数y最小值为1
C.该函数y随着x的增大而增大 D.该函数图象与y轴交于
6.已知m=x+1,n=﹣x+2,若规定y=,则y的最小值为( )
A.0 B.1 C.-1 D.2
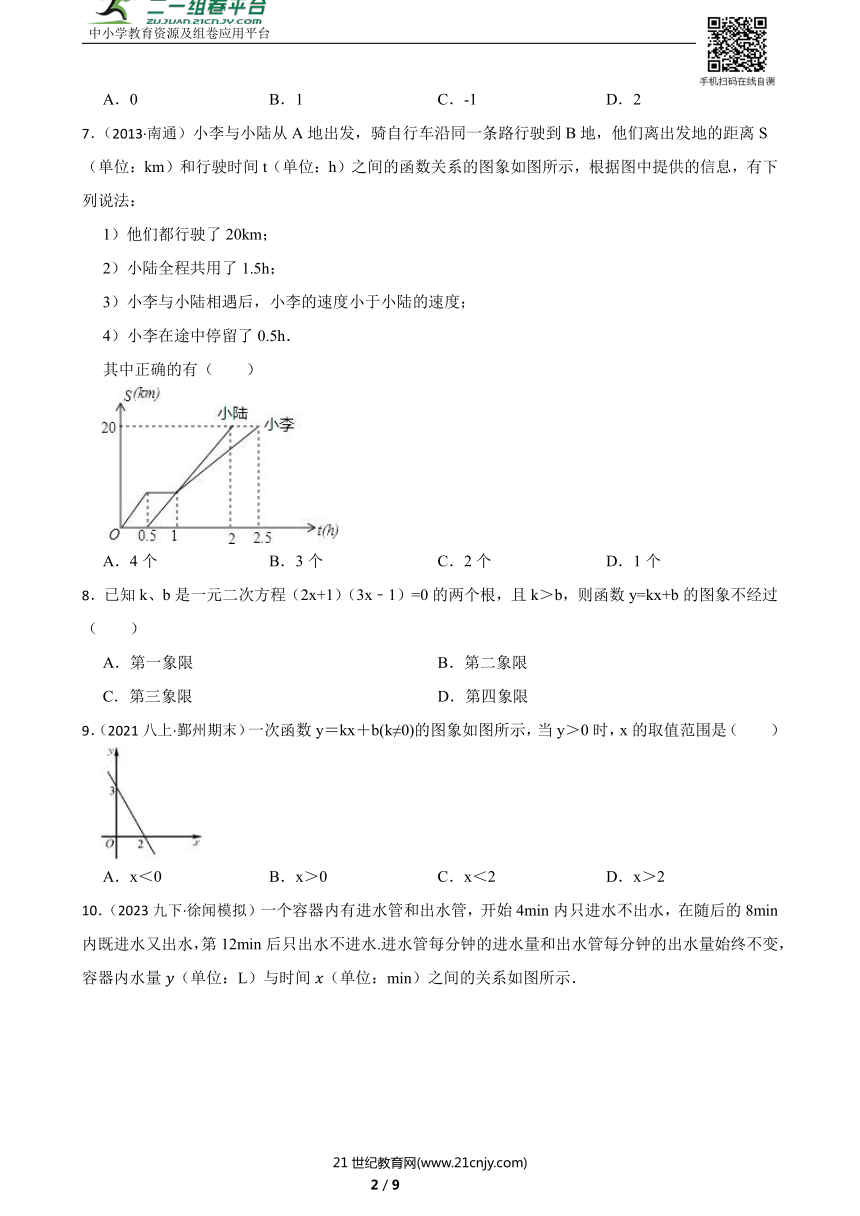
7.(2013·南通)小李与小陆从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示,根据图中提供的信息,有下列说法:
1)他们都行驶了20km;
2)小陆全程共用了1.5h;
3)小李与小陆相遇后,小李的速度小于小陆的速度;
4)小李在途中停留了0.5h.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
8.已知k、b是一元二次方程(2x+1)(3x﹣1)=0的两个根,且k>b,则函数y=kx+b的图象不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
9.(2021八上·鄞州期末)一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是( )
A.x<0 B.x>0 C.x<2 D.x>2
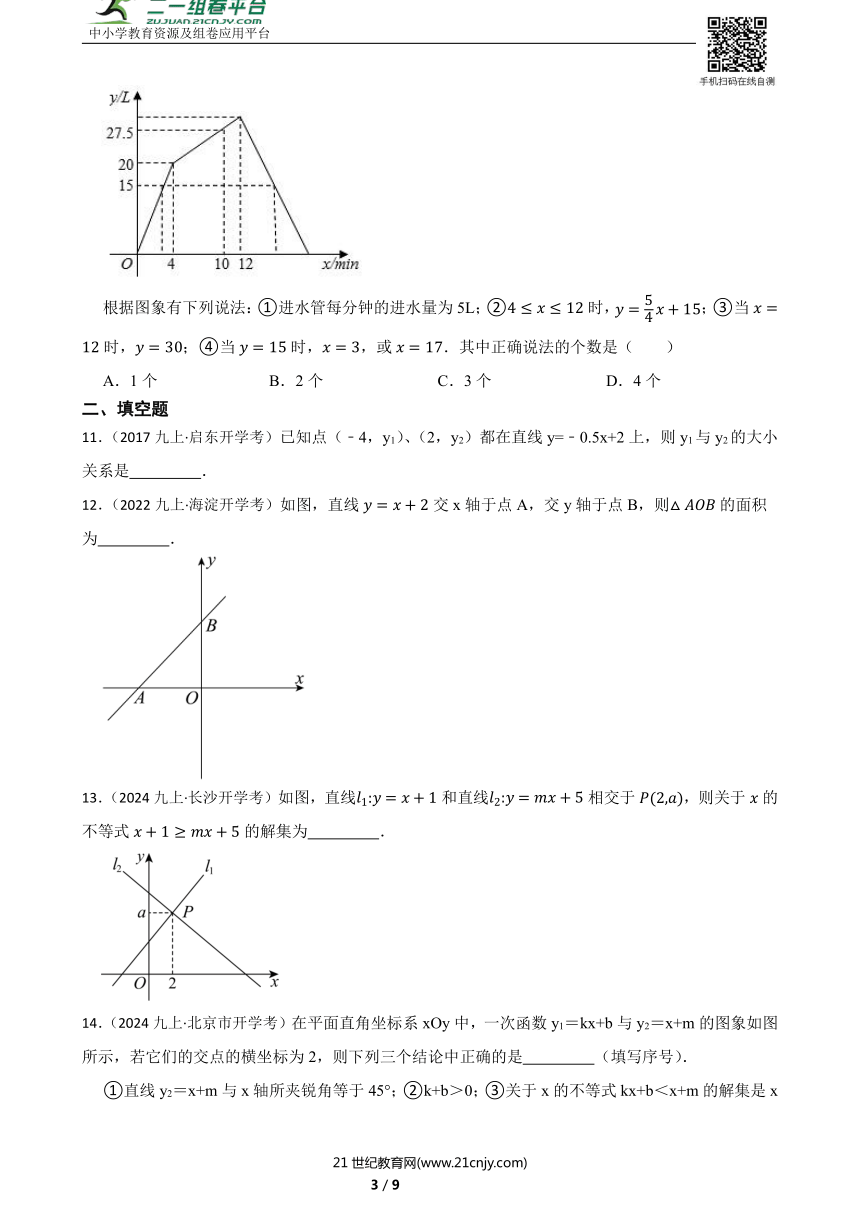
10.(2023九下·徐闻模拟)一个容器内有进水管和出水管,开始4min内只进水不出水,在随后的8min内既进水又出水,第12min后只出水不进水.进水管每分钟的进水量和出水管每分钟的出水量始终不变,容器内水量(单位:L)与时间(单位:min)之间的关系如图所示.
根据图象有下列说法:①进水管每分钟的进水量为5L;②时,;③当时,;④当时,,或.其中正确说法的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.(2017九上·启东开学考)已知点(﹣4,y1)、(2,y2)都在直线y=﹣0.5x+2上,则y1与y2的大小关系是 .
12.(2022九上·海淀开学考)如图,直线交x轴于点A,交y轴于点B,则的面积为 .
13.(2024九上·长沙开学考)如图,直线和直线相交于,则关于的不等式的解集为 .
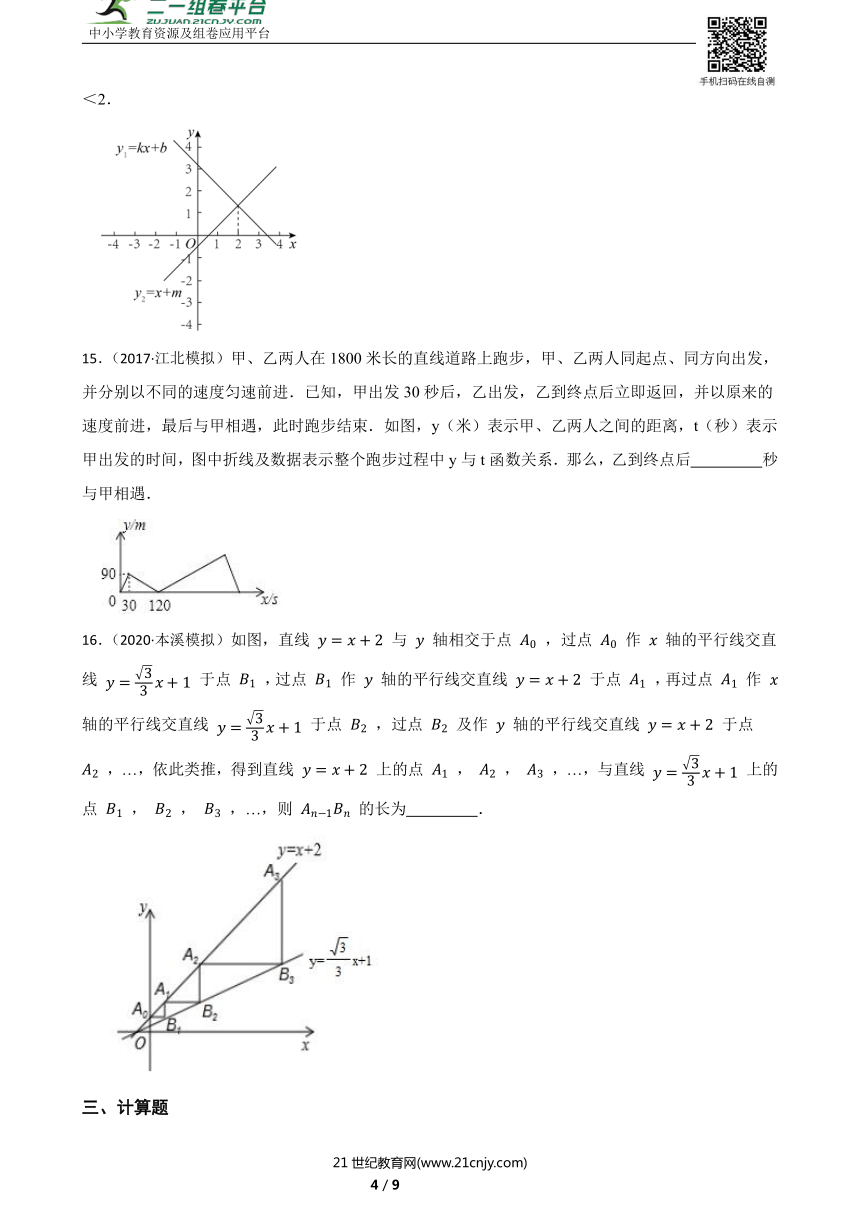
14.(2024九上·北京市开学考)在平面直角坐标系xOy中,一次函数y1=kx+b与y2=x+m的图象如图所示,若它们的交点的横坐标为2,则下列三个结论中正确的是 (填写序号).
①直线y2=x+m与x轴所夹锐角等于45°;②k+b>0;③关于x的不等式kx+b<x+m的解集是x<2.
15.(2017·江北模拟)甲、乙两人在1800米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,t(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与t函数关系.那么,乙到终点后 秒与甲相遇.
16.(2020·本溪模拟)如图,直线 与 轴相交于点 ,过点 作 轴的平行线交直线 于点 ,过点 作 轴的平行线交直线 于点 ,再过点 作 轴的平行线交直线 于点 ,过点 及作 轴的平行线交直线 于点 ,…,依此类推,得到直线 上的点 , , ,…,与直线 上的点 , , ,…,则 的长为 .
三、计算题
17.(2023九下·桂林模拟)某学校要在甲、乙两家印刷厂中选择一家印制一批《学生手册》,甲印刷厂提出:每本收元印刷费,另收元制版费;乙印刷厂提出:每本收元印刷费,不收制版费.
(1)分别写出在甲、乙两厂印制《学生手册》的费用(元),(元)与印制数量(本)之间的关系式;
(2)问该学校如何选择印刷厂印制《学生手册》比较合算?请通过计算说明理由.
18.已知y是x的一次函数,当x=3时,y=1;当x=﹣2时,y=﹣4,求这个一次函数的解析式.
四、解答题
19.(2024九下·花溪模拟)如图,二次函数 的图象与一次函数的图象交于A,B两点,点A的坐标为 .
(1)求k的值;
(2)点M是线段上的动点,将点M向上平移 ()个单位得到点N,若点N在二次函数的图象上,求h的最大值;
(3)在(2)的条件下,若 ,线段与二次函数的图象有公共点,求点M的横坐标m的取值范围.
20.(2024九下·石家庄模拟)学校计划拿出一笔钱给一些班级配置篮球和排球.若给每班1个篮球和2个排球,花完这笔钱刚好配置30个班:若给每班2个篮球和1个排球,花完这笔钱刚好配置20个班.设每个篮球a元,每个排球b元.
(1)用含b的代数式表示a;
(2)现在给每班x个篮球和y个排球,花完这笔钱刚好配置10个班.
①求y与x的函数解析式;
②怎样的配置方案,可以使每班配置的排球最少?
21.(2024·四平模拟)如图是某机场监控屏显示两飞机的飞行图象,1号指挥机(看成点P)始终以3km/min的速度在离地面5km高的上空匀速向右飞行,2号试飞机(看成点Q)一直保持在1号机P的正下方.2号机从原点O处沿函数关系式为的射线OA方向爬升,到4km高的A处便立刻转为水平飞行,再过1min到达B处开始沿直线BC降落,要求1min后到达高度为3km的点C处.
(1)求2号机的爬升速度;
(2)求BC的h关于s的函数关系式,并预计2号机着陆点的坐标;
(3)通过计算说明两机距离PQ不超过3km的时长是多少.
22.(2023九下·佛山月考)如图,已知是一次函数和反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;(2)求△AOB的面积.
答案解析部分
1.【答案】C
【知识点】一次函数图象、性质与系数的关系
2.【答案】C
【知识点】一次函数的性质
3.【答案】A
【知识点】一次函数图象、性质与系数的关系
4.【答案】C
【知识点】一次函数的其他应用
5.【答案】C
【知识点】一次函数的图象;一次函数图象与坐标轴交点问题
6.【答案】B
【知识点】一次函数的性质
7.【答案】A
【知识点】一次函数的实际应用
8.【答案】B
【知识点】一次函数图象与几何变换
9.【答案】C
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系
10.【答案】C
【知识点】一次函数的其他应用
11.【答案】y1>y2
【知识点】一次函数的性质
12.【答案】2
【知识点】一次函数的实际应用-几何问题
13.【答案】
【知识点】一次函数与不等式(组)的关系
14.【答案】①②
【知识点】一次函数与不等式(组)的关系
15.【答案】
【知识点】一次函数的实际应用
16.【答案】
【知识点】与一次函数相关的规律问题
17.【答案】(1),;
(2)该学校印制学生手册数量小于本时应选择乙厂合算,当印制学生手册数量大于本时应选择甲厂合算,当印制学生手册数量等于本时选择两厂费用都一样
【知识点】一次函数的其他应用
18.【答案】【解答】解:设一次函数解析式为y=kx+b,
将x=3,y=1;x=﹣2,y=﹣4代入得:,
解得:k=1,b=﹣2.
则一次函数解析式为y=x﹣2.
【知识点】待定系数法求一次函数解析式
19.【答案】(1)k的值为
(2)h的最大值为
(3)或
【知识点】待定系数法求一次函数解析式
20.【答案】(1)a=4b;(2)①;②给每班4个篮球和2个排球
【知识点】一次函数的实际应用-方案问题
21.【答案】(1)解:∵2号试飞机(看成点Q)一直保持在1号机P的正下方,
∴1号飞机和2号飞机在水平方向上通过相等的距离所用时间相等.
∵,∴当时,.
∴点A的坐标为(4,4).
∴2号飞机从点O到点A飞行的距离为,所用的时间为.
∴2号机的爬升速度为;
(2)解:根据题意,得点B的横坐标为4+3×1=7,点C的横坐标为7+3×1=10,
∴点B的坐标为(7,4),点C的坐标为(10,3).
设BC的h关于s的函数关系式为(k,b为常数,且).
将和分别代入,
得解得
∴BC的h关于s的函数关系式为.
当时,得.解得.
∴预计2号机着陆点的坐标为(19,0);
(3)解:当时,当两机距离时,得,解得;
当时,当两机距离时,
得,解得.
根据函数图象,当时,两机距离PQ不超过3km,
,
∴两机距离PQ不超过3km的时长是.
【知识点】一次函数与一元一次方程的关系;一次函数的实际应用
22.【答案】(1)反比例函数解析式为,一函数解析式为;(2).
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的关系
21世纪教育网(www.21cnjy.com)
1 / 9
2025年中考数学九年级
一轮复习【函数】专题(一次函数部分)过关题
一、单选题
1.(2019·三亚模拟)一次函数y=﹣2x+5不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(2024·泰安模拟)函数的图象如图所示,则关于x的一元二次方程的根的情况是( )
A.没有实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.无法确定
3.(2022八下·大足期中)若一次函数y=(k-3)x-1的图像不经过第一象限,则( )
A.k<3 B.k>3 C.k>0 D.k<0
4.(2024八下·阳高期末)如图是1个纸杯和6个纸杯叠放在一起的示意图.小红想探究叠放在一起的杯子的总高度随杯子数量的变化关系.她将50个同样的纸杯叠放在一起,则这50个纸杯的总高度约为( )
A. B. C. D.
5.(2024九下·高邮模拟)下列关于函数的图象与性质叙述错误的是( )
A.该函数图象关于直线对称 B.该函数y最小值为1
C.该函数y随着x的增大而增大 D.该函数图象与y轴交于
6.已知m=x+1,n=﹣x+2,若规定y=,则y的最小值为( )
A.0 B.1 C.-1 D.2
7.(2013·南通)小李与小陆从A地出发,骑自行车沿同一条路行驶到B地,他们离出发地的距离S(单位:km)和行驶时间t(单位:h)之间的函数关系的图象如图所示,根据图中提供的信息,有下列说法:
1)他们都行驶了20km;
2)小陆全程共用了1.5h;
3)小李与小陆相遇后,小李的速度小于小陆的速度;
4)小李在途中停留了0.5h.
其中正确的有( )
A.4个 B.3个 C.2个 D.1个
8.已知k、b是一元二次方程(2x+1)(3x﹣1)=0的两个根,且k>b,则函数y=kx+b的图象不经过( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
9.(2021八上·鄞州期末)一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是( )
A.x<0 B.x>0 C.x<2 D.x>2
10.(2023九下·徐闻模拟)一个容器内有进水管和出水管,开始4min内只进水不出水,在随后的8min内既进水又出水,第12min后只出水不进水.进水管每分钟的进水量和出水管每分钟的出水量始终不变,容器内水量(单位:L)与时间(单位:min)之间的关系如图所示.
根据图象有下列说法:①进水管每分钟的进水量为5L;②时,;③当时,;④当时,,或.其中正确说法的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.(2017九上·启东开学考)已知点(﹣4,y1)、(2,y2)都在直线y=﹣0.5x+2上,则y1与y2的大小关系是 .
12.(2022九上·海淀开学考)如图,直线交x轴于点A,交y轴于点B,则的面积为 .
13.(2024九上·长沙开学考)如图,直线和直线相交于,则关于的不等式的解集为 .
14.(2024九上·北京市开学考)在平面直角坐标系xOy中,一次函数y1=kx+b与y2=x+m的图象如图所示,若它们的交点的横坐标为2,则下列三个结论中正确的是 (填写序号).
①直线y2=x+m与x轴所夹锐角等于45°;②k+b>0;③关于x的不等式kx+b<x+m的解集是x<2.
15.(2017·江北模拟)甲、乙两人在1800米长的直线道路上跑步,甲、乙两人同起点、同方向出发,并分别以不同的速度匀速前进.已知,甲出发30秒后,乙出发,乙到终点后立即返回,并以原来的速度前进,最后与甲相遇,此时跑步结束.如图,y(米)表示甲、乙两人之间的距离,t(秒)表示甲出发的时间,图中折线及数据表示整个跑步过程中y与t函数关系.那么,乙到终点后 秒与甲相遇.
16.(2020·本溪模拟)如图,直线 与 轴相交于点 ,过点 作 轴的平行线交直线 于点 ,过点 作 轴的平行线交直线 于点 ,再过点 作 轴的平行线交直线 于点 ,过点 及作 轴的平行线交直线 于点 ,…,依此类推,得到直线 上的点 , , ,…,与直线 上的点 , , ,…,则 的长为 .
三、计算题
17.(2023九下·桂林模拟)某学校要在甲、乙两家印刷厂中选择一家印制一批《学生手册》,甲印刷厂提出:每本收元印刷费,另收元制版费;乙印刷厂提出:每本收元印刷费,不收制版费.
(1)分别写出在甲、乙两厂印制《学生手册》的费用(元),(元)与印制数量(本)之间的关系式;
(2)问该学校如何选择印刷厂印制《学生手册》比较合算?请通过计算说明理由.
18.已知y是x的一次函数,当x=3时,y=1;当x=﹣2时,y=﹣4,求这个一次函数的解析式.
四、解答题
19.(2024九下·花溪模拟)如图,二次函数 的图象与一次函数的图象交于A,B两点,点A的坐标为 .
(1)求k的值;
(2)点M是线段上的动点,将点M向上平移 ()个单位得到点N,若点N在二次函数的图象上,求h的最大值;
(3)在(2)的条件下,若 ,线段与二次函数的图象有公共点,求点M的横坐标m的取值范围.
20.(2024九下·石家庄模拟)学校计划拿出一笔钱给一些班级配置篮球和排球.若给每班1个篮球和2个排球,花完这笔钱刚好配置30个班:若给每班2个篮球和1个排球,花完这笔钱刚好配置20个班.设每个篮球a元,每个排球b元.
(1)用含b的代数式表示a;
(2)现在给每班x个篮球和y个排球,花完这笔钱刚好配置10个班.
①求y与x的函数解析式;
②怎样的配置方案,可以使每班配置的排球最少?
21.(2024·四平模拟)如图是某机场监控屏显示两飞机的飞行图象,1号指挥机(看成点P)始终以3km/min的速度在离地面5km高的上空匀速向右飞行,2号试飞机(看成点Q)一直保持在1号机P的正下方.2号机从原点O处沿函数关系式为的射线OA方向爬升,到4km高的A处便立刻转为水平飞行,再过1min到达B处开始沿直线BC降落,要求1min后到达高度为3km的点C处.
(1)求2号机的爬升速度;
(2)求BC的h关于s的函数关系式,并预计2号机着陆点的坐标;
(3)通过计算说明两机距离PQ不超过3km的时长是多少.
22.(2023九下·佛山月考)如图,已知是一次函数和反比例函数的图象的两个交点.
(1)求反比例函数和一次函数的解析式;(2)求△AOB的面积.
答案解析部分
1.【答案】C
【知识点】一次函数图象、性质与系数的关系
2.【答案】C
【知识点】一次函数的性质
3.【答案】A
【知识点】一次函数图象、性质与系数的关系
4.【答案】C
【知识点】一次函数的其他应用
5.【答案】C
【知识点】一次函数的图象;一次函数图象与坐标轴交点问题
6.【答案】B
【知识点】一次函数的性质
7.【答案】A
【知识点】一次函数的实际应用
8.【答案】B
【知识点】一次函数图象与几何变换
9.【答案】C
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系
10.【答案】C
【知识点】一次函数的其他应用
11.【答案】y1>y2
【知识点】一次函数的性质
12.【答案】2
【知识点】一次函数的实际应用-几何问题
13.【答案】
【知识点】一次函数与不等式(组)的关系
14.【答案】①②
【知识点】一次函数与不等式(组)的关系
15.【答案】
【知识点】一次函数的实际应用
16.【答案】
【知识点】与一次函数相关的规律问题
17.【答案】(1),;
(2)该学校印制学生手册数量小于本时应选择乙厂合算,当印制学生手册数量大于本时应选择甲厂合算,当印制学生手册数量等于本时选择两厂费用都一样
【知识点】一次函数的其他应用
18.【答案】【解答】解:设一次函数解析式为y=kx+b,
将x=3,y=1;x=﹣2,y=﹣4代入得:,
解得:k=1,b=﹣2.
则一次函数解析式为y=x﹣2.
【知识点】待定系数法求一次函数解析式
19.【答案】(1)k的值为
(2)h的最大值为
(3)或
【知识点】待定系数法求一次函数解析式
20.【答案】(1)a=4b;(2)①;②给每班4个篮球和2个排球
【知识点】一次函数的实际应用-方案问题
21.【答案】(1)解:∵2号试飞机(看成点Q)一直保持在1号机P的正下方,
∴1号飞机和2号飞机在水平方向上通过相等的距离所用时间相等.
∵,∴当时,.
∴点A的坐标为(4,4).
∴2号飞机从点O到点A飞行的距离为,所用的时间为.
∴2号机的爬升速度为;
(2)解:根据题意,得点B的横坐标为4+3×1=7,点C的横坐标为7+3×1=10,
∴点B的坐标为(7,4),点C的坐标为(10,3).
设BC的h关于s的函数关系式为(k,b为常数,且).
将和分别代入,
得解得
∴BC的h关于s的函数关系式为.
当时,得.解得.
∴预计2号机着陆点的坐标为(19,0);
(3)解:当时,当两机距离时,得,解得;
当时,当两机距离时,
得,解得.
根据函数图象,当时,两机距离PQ不超过3km,
,
∴两机距离PQ不超过3km的时长是.
【知识点】一次函数与一元一次方程的关系;一次函数的实际应用
22.【答案】(1)反比例函数解析式为,一函数解析式为;(2).
【知识点】待定系数法求一次函数解析式;一次函数与二元一次方程(组)的关系
21世纪教育网(www.21cnjy.com)
1 / 9
同课章节目录
