19.3 正方形 学案(含答案) 2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 19.3 正方形 学案(含答案) 2024-2025学年数学华东师大版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 303.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 00:00:00 | ||
图片预览


文档简介
第19章 矩形、菱形与正方形
19.3 正方形
1.正方形的性质
性 质:(1)正方形的 都相等;
(2)正方形的 都是直角;
(3)正方形的对角线 .
注 意:正方形是中心对称图形,对称中心是 ,也是轴对称图形,它有 条对称轴.
2.正方形的判定方法
定理1:有一个角是 的菱形是正方形.
定理2:有一组邻边 的矩形是正方形.
类型之一 正方形的性质
如图,在正方形ABCD的外侧作等边三角形ADE,连结BE、CE.
(1)求证:△BAE≌△CDE;
(2)求∠AEB的度数.
类型之二 正方形的判定
[2022·邵阳]如图,在菱形ABCD中,对角线AC与BD相交于点O,点E、F在对角线BD上,且BE=DF,OE=OA.求证:四边形AECF是正方形.
类型之三 正方形的性质与判定的综合运用
如图,E、F、M、N分别是正方形ABCD四条边上的点,AE=BF=CM=DN,四边形EFMN是什么图形?证明你的结论.
1.在四边形ABCD中,O是对角线AC与BD的交点.下列条件能判定这个四边形为正方形的是 ( )
A.AD∥BC,∠B=∠D
B.AC=BD,AB=CD,AD=BC
C.OA=OC,OB=OD,AB=BC
D.OA=OB=OC=OD,AC⊥BD
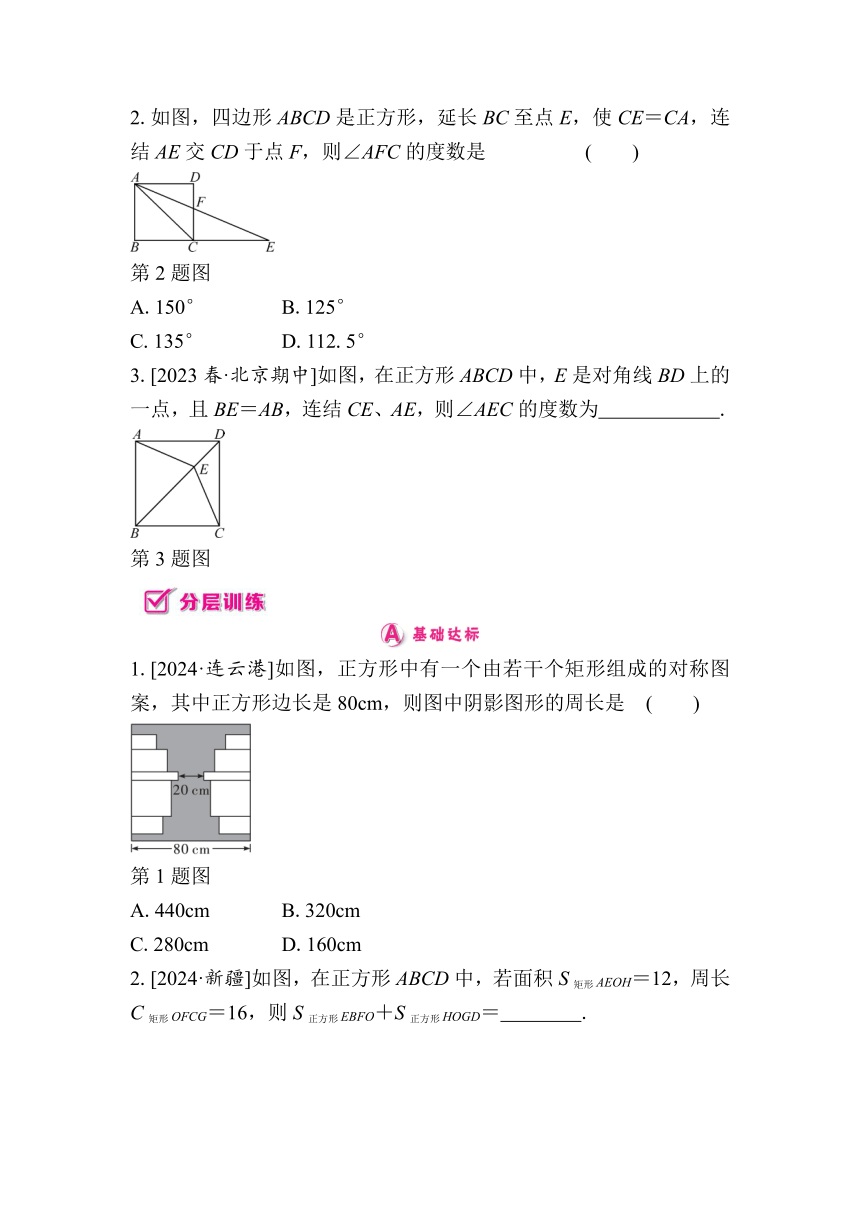
2.如图,四边形ABCD是正方形,延长BC至点E,使CE=CA,连结AE交CD于点F,则∠AFC的度数是 ( )
第2题图
A.150° B.125°
C.135° D.112.5°
3.[2023春·北京期中]如图,在正方形ABCD中,E是对角线BD上的一点,且BE=AB,连结CE、AE,则∠AEC的度数为 .
第3题图
1.[2024·连云港]如图,正方形中有一个由若干个矩形组成的对称图案,其中正方形边长是80cm,则图中阴影图形的周长是 ( )
第1题图
A.440cm B.320cm
C.280cm D.160cm
2.[2024·新疆]如图,在正方形ABCD中,若面积S矩形AEOH=12,周长C矩形OFCG=16,则S正方形EBFO+S正方形HOGD= .
第2题图
3.[2022·恩施州]如图,已知四边形ABCD是正方形,G为线段AD上任意一点,CE⊥BG于点E,DF⊥CE于点F.求证:DF=BE+EF.
4.如图,E是正方形ABCD对角线BD上一点,连结AE、CE,并延长CE交AD于点F.
(1)求证:△ABE≌△CBE;
(2)若∠AEC=140°,求∠DFE的度数.
5.如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE,垂足为G.
(1)求证:AF=BE.
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?请说明理由.
6.如图,正方形ABCD的对角线AC与BD相交于点O,AB=3,E为OC上一点,OE=1,连结BE,过点A作AF⊥BE于点F,与BD交于点G.
(1)BE与AG相等吗?若相等,请证明;若不相等,请说明理由.
(2)求AF的长.
7.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,O为AB的中点,过点A作直线AE交DO的延长线于点E,使∠EAB=∠C,连结BE.
(1)求证:BC∥AE.
(2)求证:四边形AEBD是矩形.
(3)当△ABC满足什么条件时,四边形AEBD是正方形?请说明理由.
8.(推理能力)[2024春·仁寿县校级月考]如图,在正方形ABCD中,CF平分正方形的外角,点E在BC上.
(1)若AE=EF,求证:AE⊥EF;
(2)若AE⊥EF,求证:AE=EF.
参考答案
【预习导航】
1.(1)四条边 (2)四个角 (3)相等且互相垂直平分 两条对角线的交点 4
2.直角 相等
【归类探究】
【例1】(1)略 (2)∠AEB=15°
【例2】略
【例3】四边形EFMN是正方形.证明略.
【当堂测评】
1.D 2.D 3.135°
【分层训练】
1.A 2.40 3.略
4.(1)略 (2)∠DFE=65°
5.(1)略 (2)MP=NQ.理由略.
6.(1)BE=AG.证明略. (2)AF=
7.(1)略 (2)略
(3)当△ABC满足∠BAC=90°时,四边形AEBD是正方形.理由略.
8.略
。
19.3 正方形
1.正方形的性质
性 质:(1)正方形的 都相等;
(2)正方形的 都是直角;
(3)正方形的对角线 .
注 意:正方形是中心对称图形,对称中心是 ,也是轴对称图形,它有 条对称轴.
2.正方形的判定方法
定理1:有一个角是 的菱形是正方形.
定理2:有一组邻边 的矩形是正方形.
类型之一 正方形的性质
如图,在正方形ABCD的外侧作等边三角形ADE,连结BE、CE.
(1)求证:△BAE≌△CDE;
(2)求∠AEB的度数.
类型之二 正方形的判定
[2022·邵阳]如图,在菱形ABCD中,对角线AC与BD相交于点O,点E、F在对角线BD上,且BE=DF,OE=OA.求证:四边形AECF是正方形.
类型之三 正方形的性质与判定的综合运用
如图,E、F、M、N分别是正方形ABCD四条边上的点,AE=BF=CM=DN,四边形EFMN是什么图形?证明你的结论.
1.在四边形ABCD中,O是对角线AC与BD的交点.下列条件能判定这个四边形为正方形的是 ( )
A.AD∥BC,∠B=∠D
B.AC=BD,AB=CD,AD=BC
C.OA=OC,OB=OD,AB=BC
D.OA=OB=OC=OD,AC⊥BD
2.如图,四边形ABCD是正方形,延长BC至点E,使CE=CA,连结AE交CD于点F,则∠AFC的度数是 ( )
第2题图
A.150° B.125°
C.135° D.112.5°
3.[2023春·北京期中]如图,在正方形ABCD中,E是对角线BD上的一点,且BE=AB,连结CE、AE,则∠AEC的度数为 .
第3题图
1.[2024·连云港]如图,正方形中有一个由若干个矩形组成的对称图案,其中正方形边长是80cm,则图中阴影图形的周长是 ( )
第1题图
A.440cm B.320cm
C.280cm D.160cm
2.[2024·新疆]如图,在正方形ABCD中,若面积S矩形AEOH=12,周长C矩形OFCG=16,则S正方形EBFO+S正方形HOGD= .
第2题图
3.[2022·恩施州]如图,已知四边形ABCD是正方形,G为线段AD上任意一点,CE⊥BG于点E,DF⊥CE于点F.求证:DF=BE+EF.
4.如图,E是正方形ABCD对角线BD上一点,连结AE、CE,并延长CE交AD于点F.
(1)求证:△ABE≌△CBE;
(2)若∠AEC=140°,求∠DFE的度数.
5.如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE,垂足为G.
(1)求证:AF=BE.
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?请说明理由.
6.如图,正方形ABCD的对角线AC与BD相交于点O,AB=3,E为OC上一点,OE=1,连结BE,过点A作AF⊥BE于点F,与BD交于点G.
(1)BE与AG相等吗?若相等,请证明;若不相等,请说明理由.
(2)求AF的长.
7.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,O为AB的中点,过点A作直线AE交DO的延长线于点E,使∠EAB=∠C,连结BE.
(1)求证:BC∥AE.
(2)求证:四边形AEBD是矩形.
(3)当△ABC满足什么条件时,四边形AEBD是正方形?请说明理由.
8.(推理能力)[2024春·仁寿县校级月考]如图,在正方形ABCD中,CF平分正方形的外角,点E在BC上.
(1)若AE=EF,求证:AE⊥EF;
(2)若AE⊥EF,求证:AE=EF.
参考答案
【预习导航】
1.(1)四条边 (2)四个角 (3)相等且互相垂直平分 两条对角线的交点 4
2.直角 相等
【归类探究】
【例1】(1)略 (2)∠AEB=15°
【例2】略
【例3】四边形EFMN是正方形.证明略.
【当堂测评】
1.D 2.D 3.135°
【分层训练】
1.A 2.40 3.略
4.(1)略 (2)∠DFE=65°
5.(1)略 (2)MP=NQ.理由略.
6.(1)BE=AG.证明略. (2)AF=
7.(1)略 (2)略
(3)当△ABC满足∠BAC=90°时,四边形AEBD是正方形.理由略.
8.略
。
