第20章 数据的整理与初步处理 质量评估(含简单答案) 2024-2025学年数学华东师大版八年级下册
文档属性
| 名称 | 第20章 数据的整理与初步处理 质量评估(含简单答案) 2024-2025学年数学华东师大版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 331.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 00:00:00 | ||
图片预览



文档简介
第20章 数据的整理与初步处理 质量评估
[时间:120分钟 分值:150分]
一、选择题(每题3分,共30分)
1.某镇组织开展群众文化赛事活动,其中参赛的六个村得分分别为55,64,51,50,61,55,则这组数据的中位数是 ( )
A.53 B.55 C.58 D.64
2.在学校群文阅读活动中,某学习小组五名同学阅读课外书的本数分别为3,5,7,4,5.这组数据中的中位数和众数分别是 ( )
A.3,4 B.4,4 C.4,5 D.5,5
3.小明在一次射击训练中,连续10次的成绩为1次10环,3次9环,6次8环,则小明这10次射击的平均成绩为 ( )
A.8.5环 B.8.6环 C.8.7环 D.8.8环
4.第8个全国近视防控宣传教育月的主题是“有效减少近视发生,共同守护光明未来”.某校积极响应,开展视力检查.某班45名同学视力检查数据如下表:
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 1 4 4 7 11 10 5 3
这45名同学视力检查数据的众数是 ( )
A.4.6 B.4.7 C.4.8 D.4.9
5.为了推进“阳光体育”,学校积极开展球类运动,在一次定点投篮测试中,每人投篮5次,七年级某班统计全班50名学生投中的次数,并记录如下:
投中次数(个) 0 1 2 3 4 5
人数(人) 1 ● 10 17 ● 6
表格中有两处数据不小心被墨汁遮盖了,下列关于投中次数的统计量中可以确定的是 ( )
A.平均数 B.中位数 C.众数 D.方差
6.为了解“睡眠管理”落实情况,某中学随机调查了50名学生的每天平均睡眠时间(时间均保留整数),将样本数据绘制成统计图(如图),其中有两个数据被遮盖.关于睡眠时间的统计量中,与被遮盖的数据无关的是 ( )
第6题图
A.平均数 B.中位数 C.众数 D.方差
7.学校开展“书香校园,师生共读”活动,某学习小组五名同学一周的课外阅读时间(单位:h)分别为4,5,5,6,10.这组数据的平均数、方差分别是 ( )
A.6,4.4 B.5,6 C.6,4.2 D.6,5
8.射击运动队进行射击测试,甲、乙两名选手的测试成绩如图,其成绩的方差分别记为和,则和的大小关系是 ( )
(甲)
(乙)
A.> B.< C.= D.无法确定
9.数据1,2,3,4,5,x存在唯一众数,且该组数据的平均数等于众数,则x的值为( )
A.2 B.3 C.4 D.5
10.某次射击比赛,甲队员的成绩如图,根据此统计图,下列结论中错误的是 ( )
第10题图
A.最高成绩是9.4环 B.平均成绩是9环
C.这组成绩的众数是9环 D.这组成绩的方差是8.7
二、填空题(每题4分,共24分)
11.学校要从王静、李玉两位同学中选拔1人参加运动会志愿者工作,选拔项目为普通话、体育知识和旅游知识,并将成绩依次按4∶3∶3记分.两人的各项选拔成绩如下表所示,则最终胜出的同学是 .
普通话 体育知识 旅游知识
王静 80 90 70
李玉 90 80 70
12.某校生物小组的9名同学各用100粒种子做发芽试验,几天后观察并记录种子的发芽数分别为89,73,90,86,75,86,89,95,89,以上数据的众数为 .
13.若一组数据6,6,m,7,7,8的众数为7,则这组数据的中位数为 .
14.某商场准备购进400双滑冰鞋,随机调查了某段时间内40双不同鞋号的滑冰鞋的销售情况,统计数据如下:
鞋号 35 36 37 38 39 40 41 42 43
销售量(双) 2 4 5 5 12 6 3 2 1
根据以上数据,估计该商场购进鞋号需求最多的滑冰鞋的数量为 双.
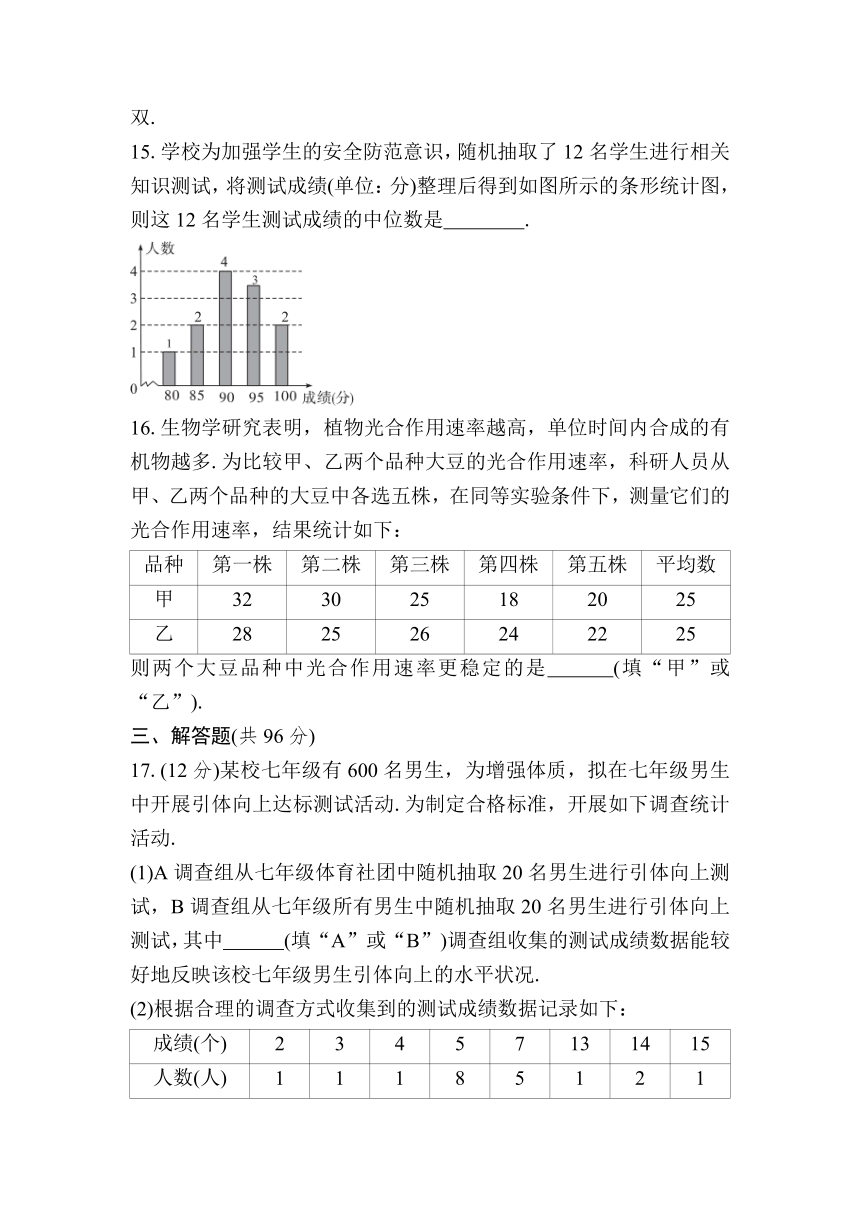
15.学校为加强学生的安全防范意识,随机抽取了12名学生进行相关知识测试,将测试成绩(单位:分)整理后得到如图所示的条形统计图,则这12名学生测试成绩的中位数是 .
16.生物学研究表明,植物光合作用速率越高,单位时间内合成的有机物越多.为比较甲、乙两个品种大豆的光合作用速率,科研人员从甲、乙两个品种的大豆中各选五株,在同等实验条件下,测量它们的光合作用速率,结果统计如下:
品种 第一株 第二株 第三株 第四株 第五株 平均数
甲 32 30 25 18 20 25
乙 28 25 26 24 22 25
则两个大豆品种中光合作用速率更稳定的是 (填“甲”或“乙”).
三、解答题(共96分)
17.(12分)某校七年级有600名男生,为增强体质,拟在七年级男生中开展引体向上达标测试活动.为制定合格标准,开展如下调查统计活动.
(1)A调查组从七年级体育社团中随机抽取20名男生进行引体向上测试,B调查组从七年级所有男生中随机抽取20名男生进行引体向上测试,其中 (填“A”或“B”)调查组收集的测试成绩数据能较好地反映该校七年级男生引体向上的水平状况.
(2)根据合理的调查方式收集到的测试成绩数据记录如下:
成绩(个) 2 3 4 5 7 13 14 15
人数(人) 1 1 1 8 5 1 2 1
这组测试成绩的平均数为 个,中位数为 个;
(3)若以(2)中测试成绩的中位数作为该校七年级男生引体向上的合格标准,请估计该校七年级有多少名男生不能达到合格标准?
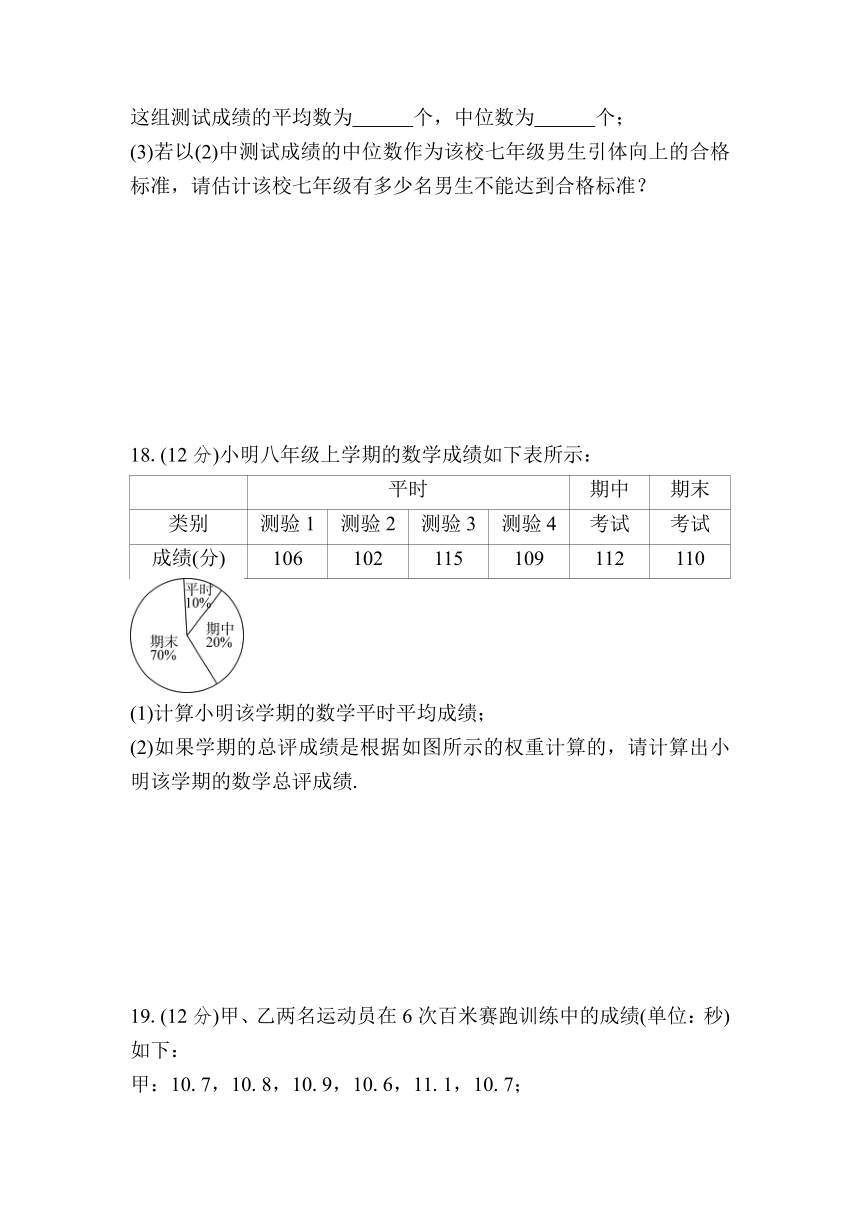
18.(12分)小明八年级上学期的数学成绩如下表所示:
平时 期中 期末
类别 测验1 测验2 测验3 测验4 考试 考试
成绩(分) 106 102 115 109 112 110
(1)计算小明该学期的数学平时平均成绩;
(2)如果学期的总评成绩是根据如图所示的权重计算的,请计算出小明该学期的数学总评成绩.
19.(12分)甲、乙两名运动员在6次百米赛跑训练中的成绩(单位:秒)如下:
甲:10.7,10.8,10.9,10.6,11.1,10.7;
乙:10.9,10.8,10.8,10.5,10.9,10.9.
(1)求甲、乙两运动员训练成绩的平均数.
(2)哪名运动员训练的成绩比较稳定?并说明理由.
20.(15分)某学校从九年级同学中任意选取40人,平均分成甲、乙两个小组进行体能测试,根据测试成绩绘制出如下的统计表和统计图(成绩均为整数,满分为10分).
甲组成绩统计表
成绩 7 8 9 10
人数 1 9 5 5
乙组成绩统计图
请根据上面的信息,解答下列问题:
(1)m= ,甲组成绩的众数是 ,乙组成绩的中位数是 ;
(2)已知甲组成绩的方差=0.81,求出乙组成绩的方差,并判断哪个小组的成绩更加稳定?
21.(15分)为提升学生身体健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,根据他们在近六场比赛中的得分、篮板和失误三个方面绘制成如下的统计图和统计表.
技术统计表
队员 平均每场得分 平均每场篮板 平均每场失误
甲 26.5 8 2
乙 26 10 3
根据以上信息,回答下列问题.
(1)这六场比赛中,得分更稳定的队员是 (填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为 分.
(2)请从得分方面分析,这六场比赛中,甲、乙两名队员谁的表现更好.
(3)规定“综合得分”为:平均每场得分×1+平均每场篮板×1.5+平均每场失误×(-1),且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中,甲、乙两名队员谁的表现更好.
22.(15分)为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理分析成如下的统计图和统计表.
平均数(分) 中位数(分) 众数(分) 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请认真阅读上述信息,回答下列问题:
(1)填空:a= ,b= ,c= .
(2)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好.小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由(写出两条即可).
23.(15分)某厂生产A、B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如下统计表及折线图(不完整),并求得了A产品三次单价的平均数=5.9和方差=.
A、B产品单价变化统计表
第一次 第二次 第三次
A产品单价(元/件) 6 5.2 6.5
B产品单价(元/件) 3.5 4 3
A、B产品单价变化折线图
(1)补全图中B产品的单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %.
(2)求B产品三次单价的方差,并比较哪种产品的单价波动较小.
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),但调价后不能超过4元/件,并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
参考答案
1.B 2.D 3.A 4.B 5.C 6.B
7.A 8.A 9.B 10.D
11.李玉 12.89 13.7 14.120 15.90
16.乙
17.(1)B (2)7 5
(3)估计该校七年级有90名男生不能达到合格标准.
18.(1)小明该学期的数学平时平均成绩是108分.
(2)小明该学期的数学总评成绩是110.2分
19.(1)=10.8秒,=10.8秒.
(2)乙运动员训练成绩稳定,理由略.
20.(1)3 8 8 (2)=0.75,乙组的成绩更加稳定.
21.(1)甲 29 (2)甲队员表现更好.
(3)乙队员表现更好.
22.(1)7.5 7 25% (2)略
23.(1)补图略 25 (2)=,B产品的单价波动小. (3)m=25
。
[时间:120分钟 分值:150分]
一、选择题(每题3分,共30分)
1.某镇组织开展群众文化赛事活动,其中参赛的六个村得分分别为55,64,51,50,61,55,则这组数据的中位数是 ( )
A.53 B.55 C.58 D.64
2.在学校群文阅读活动中,某学习小组五名同学阅读课外书的本数分别为3,5,7,4,5.这组数据中的中位数和众数分别是 ( )
A.3,4 B.4,4 C.4,5 D.5,5
3.小明在一次射击训练中,连续10次的成绩为1次10环,3次9环,6次8环,则小明这10次射击的平均成绩为 ( )
A.8.5环 B.8.6环 C.8.7环 D.8.8环
4.第8个全国近视防控宣传教育月的主题是“有效减少近视发生,共同守护光明未来”.某校积极响应,开展视力检查.某班45名同学视力检查数据如下表:
视力 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 1 4 4 7 11 10 5 3
这45名同学视力检查数据的众数是 ( )
A.4.6 B.4.7 C.4.8 D.4.9
5.为了推进“阳光体育”,学校积极开展球类运动,在一次定点投篮测试中,每人投篮5次,七年级某班统计全班50名学生投中的次数,并记录如下:
投中次数(个) 0 1 2 3 4 5
人数(人) 1 ● 10 17 ● 6
表格中有两处数据不小心被墨汁遮盖了,下列关于投中次数的统计量中可以确定的是 ( )
A.平均数 B.中位数 C.众数 D.方差
6.为了解“睡眠管理”落实情况,某中学随机调查了50名学生的每天平均睡眠时间(时间均保留整数),将样本数据绘制成统计图(如图),其中有两个数据被遮盖.关于睡眠时间的统计量中,与被遮盖的数据无关的是 ( )
第6题图
A.平均数 B.中位数 C.众数 D.方差
7.学校开展“书香校园,师生共读”活动,某学习小组五名同学一周的课外阅读时间(单位:h)分别为4,5,5,6,10.这组数据的平均数、方差分别是 ( )
A.6,4.4 B.5,6 C.6,4.2 D.6,5
8.射击运动队进行射击测试,甲、乙两名选手的测试成绩如图,其成绩的方差分别记为和,则和的大小关系是 ( )
(甲)
(乙)
A.> B.< C.= D.无法确定
9.数据1,2,3,4,5,x存在唯一众数,且该组数据的平均数等于众数,则x的值为( )
A.2 B.3 C.4 D.5
10.某次射击比赛,甲队员的成绩如图,根据此统计图,下列结论中错误的是 ( )
第10题图
A.最高成绩是9.4环 B.平均成绩是9环
C.这组成绩的众数是9环 D.这组成绩的方差是8.7
二、填空题(每题4分,共24分)
11.学校要从王静、李玉两位同学中选拔1人参加运动会志愿者工作,选拔项目为普通话、体育知识和旅游知识,并将成绩依次按4∶3∶3记分.两人的各项选拔成绩如下表所示,则最终胜出的同学是 .
普通话 体育知识 旅游知识
王静 80 90 70
李玉 90 80 70
12.某校生物小组的9名同学各用100粒种子做发芽试验,几天后观察并记录种子的发芽数分别为89,73,90,86,75,86,89,95,89,以上数据的众数为 .
13.若一组数据6,6,m,7,7,8的众数为7,则这组数据的中位数为 .
14.某商场准备购进400双滑冰鞋,随机调查了某段时间内40双不同鞋号的滑冰鞋的销售情况,统计数据如下:
鞋号 35 36 37 38 39 40 41 42 43
销售量(双) 2 4 5 5 12 6 3 2 1
根据以上数据,估计该商场购进鞋号需求最多的滑冰鞋的数量为 双.
15.学校为加强学生的安全防范意识,随机抽取了12名学生进行相关知识测试,将测试成绩(单位:分)整理后得到如图所示的条形统计图,则这12名学生测试成绩的中位数是 .
16.生物学研究表明,植物光合作用速率越高,单位时间内合成的有机物越多.为比较甲、乙两个品种大豆的光合作用速率,科研人员从甲、乙两个品种的大豆中各选五株,在同等实验条件下,测量它们的光合作用速率,结果统计如下:
品种 第一株 第二株 第三株 第四株 第五株 平均数
甲 32 30 25 18 20 25
乙 28 25 26 24 22 25
则两个大豆品种中光合作用速率更稳定的是 (填“甲”或“乙”).
三、解答题(共96分)
17.(12分)某校七年级有600名男生,为增强体质,拟在七年级男生中开展引体向上达标测试活动.为制定合格标准,开展如下调查统计活动.
(1)A调查组从七年级体育社团中随机抽取20名男生进行引体向上测试,B调查组从七年级所有男生中随机抽取20名男生进行引体向上测试,其中 (填“A”或“B”)调查组收集的测试成绩数据能较好地反映该校七年级男生引体向上的水平状况.
(2)根据合理的调查方式收集到的测试成绩数据记录如下:
成绩(个) 2 3 4 5 7 13 14 15
人数(人) 1 1 1 8 5 1 2 1
这组测试成绩的平均数为 个,中位数为 个;
(3)若以(2)中测试成绩的中位数作为该校七年级男生引体向上的合格标准,请估计该校七年级有多少名男生不能达到合格标准?
18.(12分)小明八年级上学期的数学成绩如下表所示:
平时 期中 期末
类别 测验1 测验2 测验3 测验4 考试 考试
成绩(分) 106 102 115 109 112 110
(1)计算小明该学期的数学平时平均成绩;
(2)如果学期的总评成绩是根据如图所示的权重计算的,请计算出小明该学期的数学总评成绩.
19.(12分)甲、乙两名运动员在6次百米赛跑训练中的成绩(单位:秒)如下:
甲:10.7,10.8,10.9,10.6,11.1,10.7;
乙:10.9,10.8,10.8,10.5,10.9,10.9.
(1)求甲、乙两运动员训练成绩的平均数.
(2)哪名运动员训练的成绩比较稳定?并说明理由.
20.(15分)某学校从九年级同学中任意选取40人,平均分成甲、乙两个小组进行体能测试,根据测试成绩绘制出如下的统计表和统计图(成绩均为整数,满分为10分).
甲组成绩统计表
成绩 7 8 9 10
人数 1 9 5 5
乙组成绩统计图
请根据上面的信息,解答下列问题:
(1)m= ,甲组成绩的众数是 ,乙组成绩的中位数是 ;
(2)已知甲组成绩的方差=0.81,求出乙组成绩的方差,并判断哪个小组的成绩更加稳定?
21.(15分)为提升学生身体健康水平,促进学生全面发展,学校开展了丰富多彩的课外体育活动.在八年级组织的篮球联赛中,甲、乙两名队员表现优异,根据他们在近六场比赛中的得分、篮板和失误三个方面绘制成如下的统计图和统计表.
技术统计表
队员 平均每场得分 平均每场篮板 平均每场失误
甲 26.5 8 2
乙 26 10 3
根据以上信息,回答下列问题.
(1)这六场比赛中,得分更稳定的队员是 (填“甲”或“乙”);甲队员得分的中位数为27.5分,乙队员得分的中位数为 分.
(2)请从得分方面分析,这六场比赛中,甲、乙两名队员谁的表现更好.
(3)规定“综合得分”为:平均每场得分×1+平均每场篮板×1.5+平均每场失误×(-1),且综合得分越高表现越好.请利用这种评价方法,比较这六场比赛中,甲、乙两名队员谁的表现更好.
22.(15分)为激发青少年崇尚科学、探索未知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理分析成如下的统计图和统计表.
平均数(分) 中位数(分) 众数(分) 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请认真阅读上述信息,回答下列问题:
(1)填空:a= ,b= ,c= .
(2)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好.小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由(写出两条即可).
23.(15分)某厂生产A、B两种产品,其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况,绘制了如下统计表及折线图(不完整),并求得了A产品三次单价的平均数=5.9和方差=.
A、B产品单价变化统计表
第一次 第二次 第三次
A产品单价(元/件) 6 5.2 6.5
B产品单价(元/件) 3.5 4 3
A、B产品单价变化折线图
(1)补全图中B产品的单价变化的折线图,B产品第三次的单价比上一次的单价降低了 %.
(2)求B产品三次单价的方差,并比较哪种产品的单价波动较小.
(3)该厂决定第四次调价,A产品的单价仍为6.5元/件,B产品的单价比3元/件上调m%(m>0),但调价后不能超过4元/件,并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1,求m的值.
参考答案
1.B 2.D 3.A 4.B 5.C 6.B
7.A 8.A 9.B 10.D
11.李玉 12.89 13.7 14.120 15.90
16.乙
17.(1)B (2)7 5
(3)估计该校七年级有90名男生不能达到合格标准.
18.(1)小明该学期的数学平时平均成绩是108分.
(2)小明该学期的数学总评成绩是110.2分
19.(1)=10.8秒,=10.8秒.
(2)乙运动员训练成绩稳定,理由略.
20.(1)3 8 8 (2)=0.75,乙组的成绩更加稳定.
21.(1)甲 29 (2)甲队员表现更好.
(3)乙队员表现更好.
22.(1)7.5 7 25% (2)略
23.(1)补图略 25 (2)=,B产品的单价波动小. (3)m=25
。
