2025年中考数学九年级一轮复习【函数】专题(二次函数部分)过关题(含答案)
文档属性
| 名称 | 2025年中考数学九年级一轮复习【函数】专题(二次函数部分)过关题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 158.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 14:23:43 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年中考数学九年级
一轮复习【函数】专题(二次函数部分)过关题
一、单选题
1.(2023九上·竞秀期末)对于题目“一段抛物线L:与直线l:有唯一公共点.若c为整数,确定所有c的值.”甲的结果是,乙的结果是的整数,丙的结果是的整数,则( )
A.甲、乙的结果合在一起才正确
B.乙、丙的结果合在一起才正确
C.甲、丙的结果合在一起才正确
D.甲、乙、丙的结果合在一起才正确
2.(2024九上·拱墅月考)二次函数的图象向左平移个单位后的函数为( )
A. B.
C. D.
3.(2024九下·呼兰模拟)把抛物线向左平移2个单位,再向下平移3个单位,所得抛物线解析式为( )
A. B.
C. D.
4.(2023九上·武昌期中)将抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,所得到的抛物线为( )
A.y=(x+3)2+5 B.y=(x-3)2+5
C.y=(x+5)2+3 D.y=(x-5)2+3
5.(2024九下·深圳模拟)在平面直角坐标系中,将抛物线y=x2向上平移2个单位长度,再向右平移1个单位长度,得到的抛物线的解析式是( )
A.y=(x﹣1)2+2 B.y=(x﹣1)2﹣2
C.y=(x+1)2﹣2 D.y=(x+1)2+2
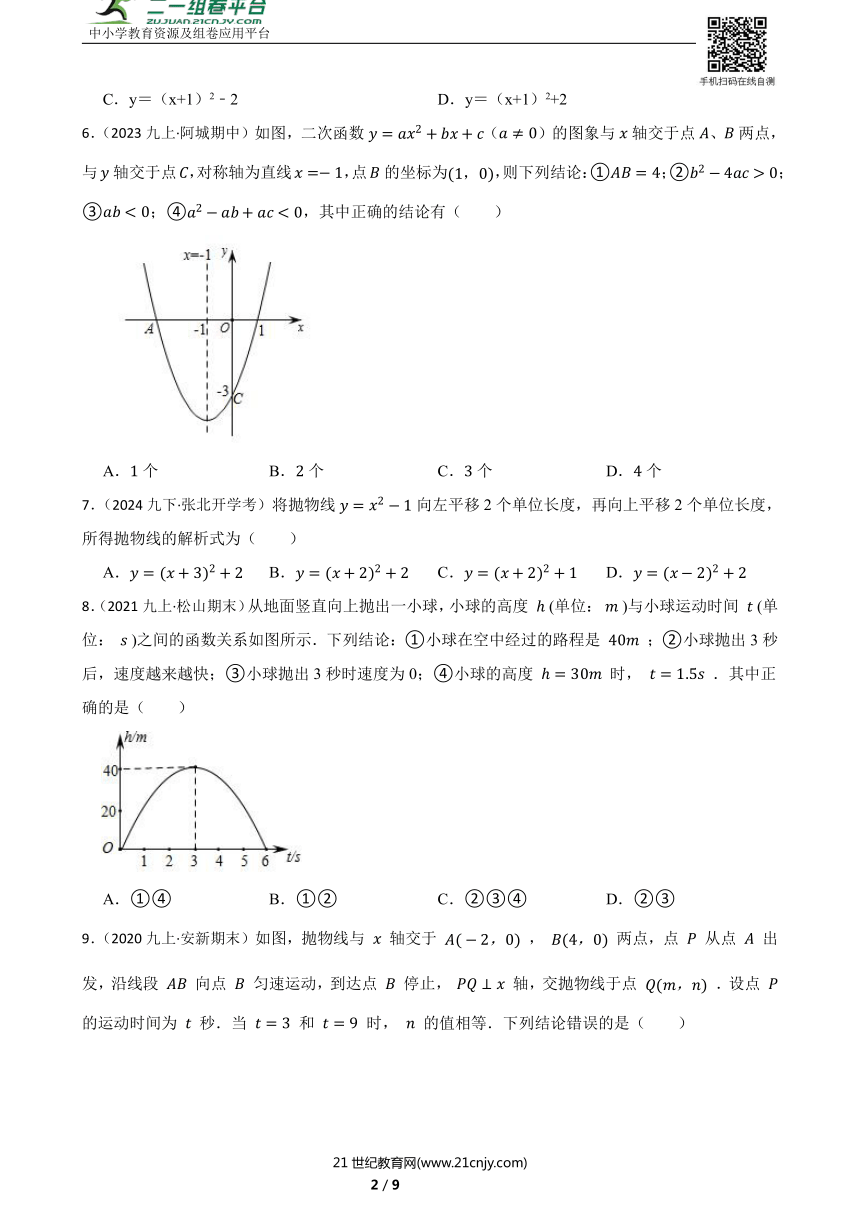
6.(2023九上·阿城期中)如图,二次函数()的图象与轴交于点、两点,与轴交于点,对称轴为直线,点的坐标为,则下列结论:①;②;③;④,其中正确的结论有( )
A.个 B.个 C.个 D.个
7.(2024九下·张北开学考)将抛物线向左平移2个单位长度,再向上平移2个单位长度,所得抛物线的解析式为( )
A. B. C. D.
8.(2021九上·松山期末)从地面竖直向上抛出一小球,小球的高度 (单位: )与小球运动时间 (单位: )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是 ;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度 时, .其中正确的是( )
A.①④ B.①② C.②③④ D.②③
9.(2020九上·安新期末)如图,抛物线与 轴交于 , 两点,点 从点 出发,沿线段 向点 匀速运动,到达点 停止, 轴,交抛物线于点 .设点 的运动时间为 秒.当 和 时, 的值相等.下列结论错误的是( )
A. 时, 的值最大
B. 时,
C.当 和 时, 的值不一定相等
D. 时,
10.(2020九上·乳山期末)二次函数 的图象与 轴的一个交点为 ,对称轴为直线 ,一次函数 的图象过点 和二次函数 图象的顶点.下列结论:( )
① ;②若 ,则 ;③若二次函数 的值大于 ,则 ;④过动点 且垂直于 轴的直线与函数 的图象的交点分别为 ,当点 位于点 上方时, 的取值范围是 或 .
错误的是( )
A.① B.② C.③ D.④
二、填空题
11.(2024九上·苏州月考)如图,抛物线与直线交于两点,则不等式的解集是 .
12.(2020九上·永善月考)抛物线 经过点A ,点B ,点C 三点,且对称轴为直线 ,则 的大小关系是 .
13.(2023·常州模拟)下表中两个变量y与x的数据满足我们初中学过的二次函数关系:
… -1 0 1 3 …
… 0 3 4 0 …
则这个二次函数图象的对称轴为 .
14.(2016九上·洪山期中)直线y=m是平行于x轴的直线,将抛物线y=﹣ x2﹣4x在直线y=m上侧的部分沿直线y=m翻折,翻折后的部分与没有翻折的部分组成新的函数图象,若新的函数图象刚好与直线y=﹣x有3个交点,则满足条件的m的值为 .
15.(2024九下·通辽月考)如图,二次函数的函数图象经过点,且与x轴交点的横坐标分别为、,其中 下列结论: ①; ②; ③; ④当 时,;⑤, 其中正确的有 . (填写正确的序号)
16.(2023九上·义乌月考)对于二次函数,规定函数是它的相关函数.已知点,的坐标分别为,,连接,若线段与二次函数的相关函数的图象有两个公共点,则的取值范围为 .
三、计算题
17.(2023九上·越城期中)
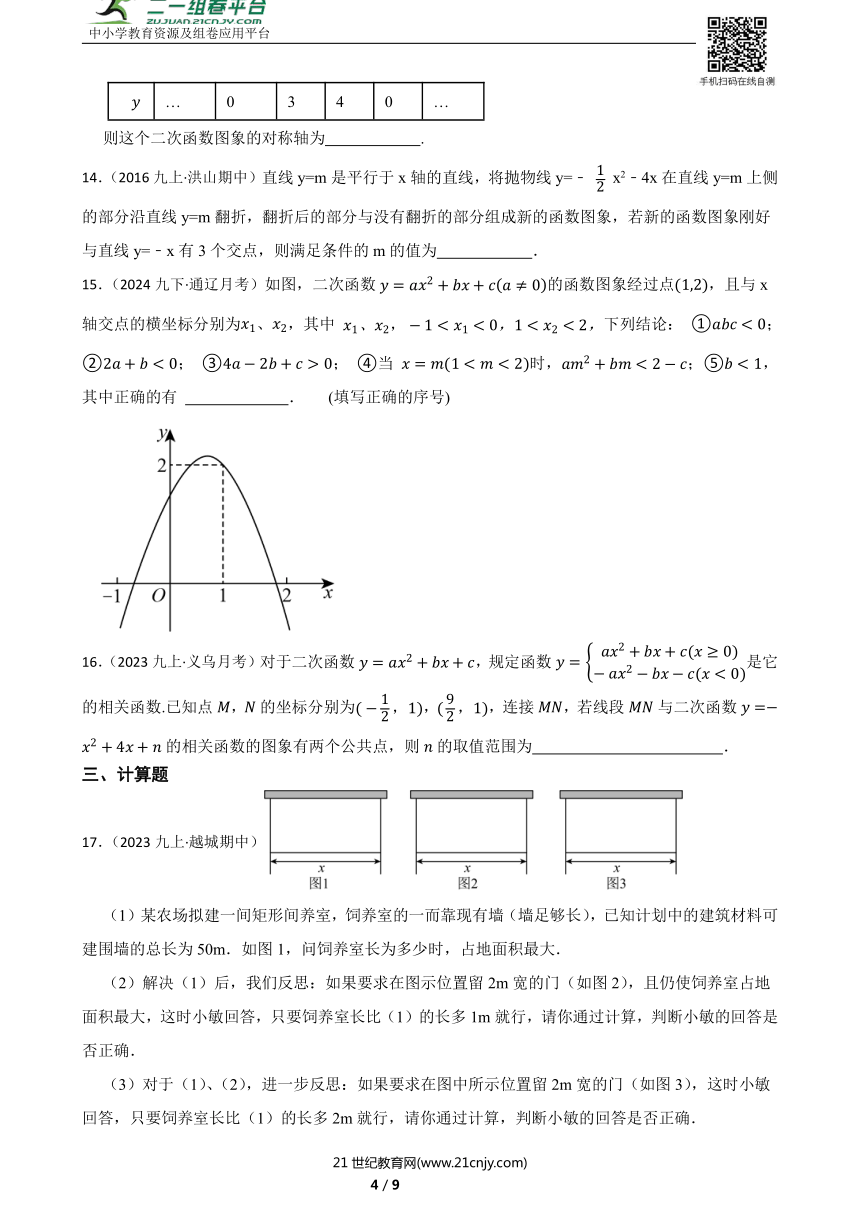
(1)某农场拟建一间矩形间养室,饲养室的一而靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50m.如图1,问饲养室长为多少时,占地面积最大.
(2)解决(1)后,我们反思:如果要求在图示位置留2m宽的门(如图2),且仍使饲养室占地面积最大,这时小敏回答,只要饲养室长比(1)的长多1m就行,请你通过计算,判断小敏的回答是否正确.
(3)对于(1)、(2),进一步反思:如果要求在图中所示位置留2m宽的门(如图3),这时小敏回答,只要饲养室长比(1)的长多2m就行,请你通过计算,判断小敏的回答是否正确.
18.(2023九上·萧山期末)已知二次函数(a为常数,且)
(1)若函数图象过点,求a的值;
(2)当时,函数的最大值为M,最小值为N,若,求a的值.
19.(2024九下·云南模拟)在平面直角坐标系中,抛物线(b是常数)经过点.点A在抛物线上,且点A的横坐标为.以点A为中心,构造正方形且轴.
(1)若点B是抛物线上一点,且在抛物线对称轴左侧.过点B作x轴的平行线交抛物线于另一点C,连接BC.当时,求点B的坐标;
(2)若,当抛物线在正方形内部的点的纵坐标y随x的增大而增大时,或者y随x的增大而减小时,求m的取值范围.
四、解答题
20.(2023九上·西和期中)某二次函数图象的顶点为,且它与轴交点的纵坐标为5,求这个二次函数的解析式.
21.(2024九上·青山湖月考)已知y关于 x的函数y=(m2+2m)x2+mx+m+1.
(1)当m为何值时,此函数是一次函数?
(2)当m为何值时,此函数是二次函数?
22.(2023九上·疏勒月考)如图,抛物线与x轴的两个交点分别为.
(1)求这条抛物线对应函数的表达式;
(2)若P点在该抛物线上,求当的面积为8时,点P的坐标.
(3)直接写出时,x的取值范围.
23.(2023九下·岳阳开学考)如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP'C,若四边形POP'C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
答案解析部分
1.【答案】C
【知识点】二次函数的实际应用-几何问题;利用二次函数图象判断一元二次方程根的情况
2.【答案】B
【知识点】二次函数图象的几何变换
3.【答案】C
【知识点】二次函数图象的几何变换
4.【答案】D
【知识点】二次函数图象的几何变换
5.【答案】A
【知识点】二次函数图象的几何变换
6.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征;利用二次函数图象判断一元二次方程根的情况
7.【答案】C
【知识点】二次函数图象的几何变换
8.【答案】D
【知识点】二次函数图象与系数的关系
9.【答案】C
【知识点】二次函数-动态几何问题
10.【答案】C
【知识点】二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质;二次函数的其他应用
11.【答案】-1<x<2
【知识点】二次函数与不等式(组)的综合应用
12.【答案】 (或 )
【知识点】二次函数图象与系数的关系
13.【答案】直线x=1
【知识点】二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的性质
14.【答案】6或
【知识点】二次函数图象的几何变换
15.【答案】 ①②④⑤
【知识点】二次函数图象与系数的关系;利用二次函数图象判断一元二次方程根的情况
16.【答案】或
【知识点】二次函数图象与坐标轴的交点问题;二次函数与不等式(组)的综合应用;二次函数图象上点的坐标特征
17.【答案】(1)饲养室长x为25m时,占地面积y最大
(2)小敏的说法正确
(3)小敏的说法正确
【知识点】二次函数的实际应用-几何问题
18.【答案】(1)解:函数图象过点得
解得:;
(2)解:由可知对称轴为直线,
①当时,开口方向向上,
当时,有时取最小值,时取最大值,
,,
∵,
∴,
解得:;
②当时,开口方向向下,
当时,有时取最大值,时取最小值,
,,
∵,
解得: ;
综上所述,.
【知识点】二次函数的最值;待定系数法求二次函数解析式;二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
19.【答案】(1)
(2)m的取值范围是或
【知识点】待定系数法求二次函数解析式;二次函数-特殊四边形存在性问题
20.【答案】
【知识点】待定系数法求二次函数解析式
21.【答案】(1)m=-2;(2)m≠﹣2且m≠0
【知识点】二次函数的定义
22.【答案】(1)
(2)
(3)
【知识点】待定系数法求二次函数解析式
23.【答案】(1))y=﹣x2+2x+3
(2)(,)
(3)当点P的坐标为(,)时,四边形ACPB的最大面积值为
【知识点】二次函数-面积问题
21世纪教育网(www.21cnjy.com)
2 / 9
2025年中考数学九年级
一轮复习【函数】专题(二次函数部分)过关题
一、单选题
1.(2023九上·竞秀期末)对于题目“一段抛物线L:与直线l:有唯一公共点.若c为整数,确定所有c的值.”甲的结果是,乙的结果是的整数,丙的结果是的整数,则( )
A.甲、乙的结果合在一起才正确
B.乙、丙的结果合在一起才正确
C.甲、丙的结果合在一起才正确
D.甲、乙、丙的结果合在一起才正确
2.(2024九上·拱墅月考)二次函数的图象向左平移个单位后的函数为( )
A. B.
C. D.
3.(2024九下·呼兰模拟)把抛物线向左平移2个单位,再向下平移3个单位,所得抛物线解析式为( )
A. B.
C. D.
4.(2023九上·武昌期中)将抛物线y=x2向上平移3个单位长度,再向右平移5个单位长度,所得到的抛物线为( )
A.y=(x+3)2+5 B.y=(x-3)2+5
C.y=(x+5)2+3 D.y=(x-5)2+3
5.(2024九下·深圳模拟)在平面直角坐标系中,将抛物线y=x2向上平移2个单位长度,再向右平移1个单位长度,得到的抛物线的解析式是( )
A.y=(x﹣1)2+2 B.y=(x﹣1)2﹣2
C.y=(x+1)2﹣2 D.y=(x+1)2+2
6.(2023九上·阿城期中)如图,二次函数()的图象与轴交于点、两点,与轴交于点,对称轴为直线,点的坐标为,则下列结论:①;②;③;④,其中正确的结论有( )
A.个 B.个 C.个 D.个
7.(2024九下·张北开学考)将抛物线向左平移2个单位长度,再向上平移2个单位长度,所得抛物线的解析式为( )
A. B. C. D.
8.(2021九上·松山期末)从地面竖直向上抛出一小球,小球的高度 (单位: )与小球运动时间 (单位: )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是 ;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度 时, .其中正确的是( )
A.①④ B.①② C.②③④ D.②③
9.(2020九上·安新期末)如图,抛物线与 轴交于 , 两点,点 从点 出发,沿线段 向点 匀速运动,到达点 停止, 轴,交抛物线于点 .设点 的运动时间为 秒.当 和 时, 的值相等.下列结论错误的是( )
A. 时, 的值最大
B. 时,
C.当 和 时, 的值不一定相等
D. 时,
10.(2020九上·乳山期末)二次函数 的图象与 轴的一个交点为 ,对称轴为直线 ,一次函数 的图象过点 和二次函数 图象的顶点.下列结论:( )
① ;②若 ,则 ;③若二次函数 的值大于 ,则 ;④过动点 且垂直于 轴的直线与函数 的图象的交点分别为 ,当点 位于点 上方时, 的取值范围是 或 .
错误的是( )
A.① B.② C.③ D.④
二、填空题
11.(2024九上·苏州月考)如图,抛物线与直线交于两点,则不等式的解集是 .
12.(2020九上·永善月考)抛物线 经过点A ,点B ,点C 三点,且对称轴为直线 ,则 的大小关系是 .
13.(2023·常州模拟)下表中两个变量y与x的数据满足我们初中学过的二次函数关系:
… -1 0 1 3 …
… 0 3 4 0 …
则这个二次函数图象的对称轴为 .
14.(2016九上·洪山期中)直线y=m是平行于x轴的直线,将抛物线y=﹣ x2﹣4x在直线y=m上侧的部分沿直线y=m翻折,翻折后的部分与没有翻折的部分组成新的函数图象,若新的函数图象刚好与直线y=﹣x有3个交点,则满足条件的m的值为 .
15.(2024九下·通辽月考)如图,二次函数的函数图象经过点,且与x轴交点的横坐标分别为、,其中 下列结论: ①; ②; ③; ④当 时,;⑤, 其中正确的有 . (填写正确的序号)
16.(2023九上·义乌月考)对于二次函数,规定函数是它的相关函数.已知点,的坐标分别为,,连接,若线段与二次函数的相关函数的图象有两个公共点,则的取值范围为 .
三、计算题
17.(2023九上·越城期中)
(1)某农场拟建一间矩形间养室,饲养室的一而靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50m.如图1,问饲养室长为多少时,占地面积最大.
(2)解决(1)后,我们反思:如果要求在图示位置留2m宽的门(如图2),且仍使饲养室占地面积最大,这时小敏回答,只要饲养室长比(1)的长多1m就行,请你通过计算,判断小敏的回答是否正确.
(3)对于(1)、(2),进一步反思:如果要求在图中所示位置留2m宽的门(如图3),这时小敏回答,只要饲养室长比(1)的长多2m就行,请你通过计算,判断小敏的回答是否正确.
18.(2023九上·萧山期末)已知二次函数(a为常数,且)
(1)若函数图象过点,求a的值;
(2)当时,函数的最大值为M,最小值为N,若,求a的值.
19.(2024九下·云南模拟)在平面直角坐标系中,抛物线(b是常数)经过点.点A在抛物线上,且点A的横坐标为.以点A为中心,构造正方形且轴.
(1)若点B是抛物线上一点,且在抛物线对称轴左侧.过点B作x轴的平行线交抛物线于另一点C,连接BC.当时,求点B的坐标;
(2)若,当抛物线在正方形内部的点的纵坐标y随x的增大而增大时,或者y随x的增大而减小时,求m的取值范围.
四、解答题
20.(2023九上·西和期中)某二次函数图象的顶点为,且它与轴交点的纵坐标为5,求这个二次函数的解析式.
21.(2024九上·青山湖月考)已知y关于 x的函数y=(m2+2m)x2+mx+m+1.
(1)当m为何值时,此函数是一次函数?
(2)当m为何值时,此函数是二次函数?
22.(2023九上·疏勒月考)如图,抛物线与x轴的两个交点分别为.
(1)求这条抛物线对应函数的表达式;
(2)若P点在该抛物线上,求当的面积为8时,点P的坐标.
(3)直接写出时,x的取值范围.
23.(2023九下·岳阳开学考)如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP'C,若四边形POP'C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
答案解析部分
1.【答案】C
【知识点】二次函数的实际应用-几何问题;利用二次函数图象判断一元二次方程根的情况
2.【答案】B
【知识点】二次函数图象的几何变换
3.【答案】C
【知识点】二次函数图象的几何变换
4.【答案】D
【知识点】二次函数图象的几何变换
5.【答案】A
【知识点】二次函数图象的几何变换
6.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题;二次函数图象上点的坐标特征;利用二次函数图象判断一元二次方程根的情况
7.【答案】C
【知识点】二次函数图象的几何变换
8.【答案】D
【知识点】二次函数图象与系数的关系
9.【答案】C
【知识点】二次函数-动态几何问题
10.【答案】C
【知识点】二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质;二次函数的其他应用
11.【答案】-1<x<2
【知识点】二次函数与不等式(组)的综合应用
12.【答案】 (或 )
【知识点】二次函数图象与系数的关系
13.【答案】直线x=1
【知识点】二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的性质
14.【答案】6或
【知识点】二次函数图象的几何变换
15.【答案】 ①②④⑤
【知识点】二次函数图象与系数的关系;利用二次函数图象判断一元二次方程根的情况
16.【答案】或
【知识点】二次函数图象与坐标轴的交点问题;二次函数与不等式(组)的综合应用;二次函数图象上点的坐标特征
17.【答案】(1)饲养室长x为25m时,占地面积y最大
(2)小敏的说法正确
(3)小敏的说法正确
【知识点】二次函数的实际应用-几何问题
18.【答案】(1)解:函数图象过点得
解得:;
(2)解:由可知对称轴为直线,
①当时,开口方向向上,
当时,有时取最小值,时取最大值,
,,
∵,
∴,
解得:;
②当时,开口方向向下,
当时,有时取最大值,时取最小值,
,,
∵,
解得: ;
综上所述,.
【知识点】二次函数的最值;待定系数法求二次函数解析式;二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
19.【答案】(1)
(2)m的取值范围是或
【知识点】待定系数法求二次函数解析式;二次函数-特殊四边形存在性问题
20.【答案】
【知识点】待定系数法求二次函数解析式
21.【答案】(1)m=-2;(2)m≠﹣2且m≠0
【知识点】二次函数的定义
22.【答案】(1)
(2)
(3)
【知识点】待定系数法求二次函数解析式
23.【答案】(1))y=﹣x2+2x+3
(2)(,)
(3)当点P的坐标为(,)时,四边形ACPB的最大面积值为
【知识点】二次函数-面积问题
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
