华师大版七下(2024版)第五章一元一次方程 单元复习 学案
文档属性
| 名称 | 华师大版七下(2024版)第五章一元一次方程 单元复习 学案 |  | |
| 格式 | docx | ||
| 文件大小 | 76.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 16:13:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第五章 一元一次方程
小结与复习
学习目标与重难点
学习目标:
理解一元一次方程的概念及其在实际问题中的数学模型作用。
熟练正确解一元一次方程,掌握去括号、去分母、移项等步骤。
3.能够将实际问题抽象为方程,培养分析问题和应用数学解决问题的能力
学习重点:一元一次方程的标准化解法(去分母、去括号、移项等);方程与实际问题的关联性分析;方程解的验算与实际问题匹配性验证
学习难点:从实际问题中抽象出等量关系并正确列出方程;灵活选择方程的变形规则,简化计算过程;解决含多个变量或复杂条件的应用题
复习旧知
1.已知等式,则下列式子中不成立的是( )
A. B. C. D.
2.下列各式中,是方程的是( )
A. B. C. D.
3..若x=2是关于x的方程5x+a=3(x+3)的解,则a的值为 .
4.解下列方程.
(1)-2x+3=4x-9.
(2)3(x+2)-2(x+2)=2x+4.
教学过程
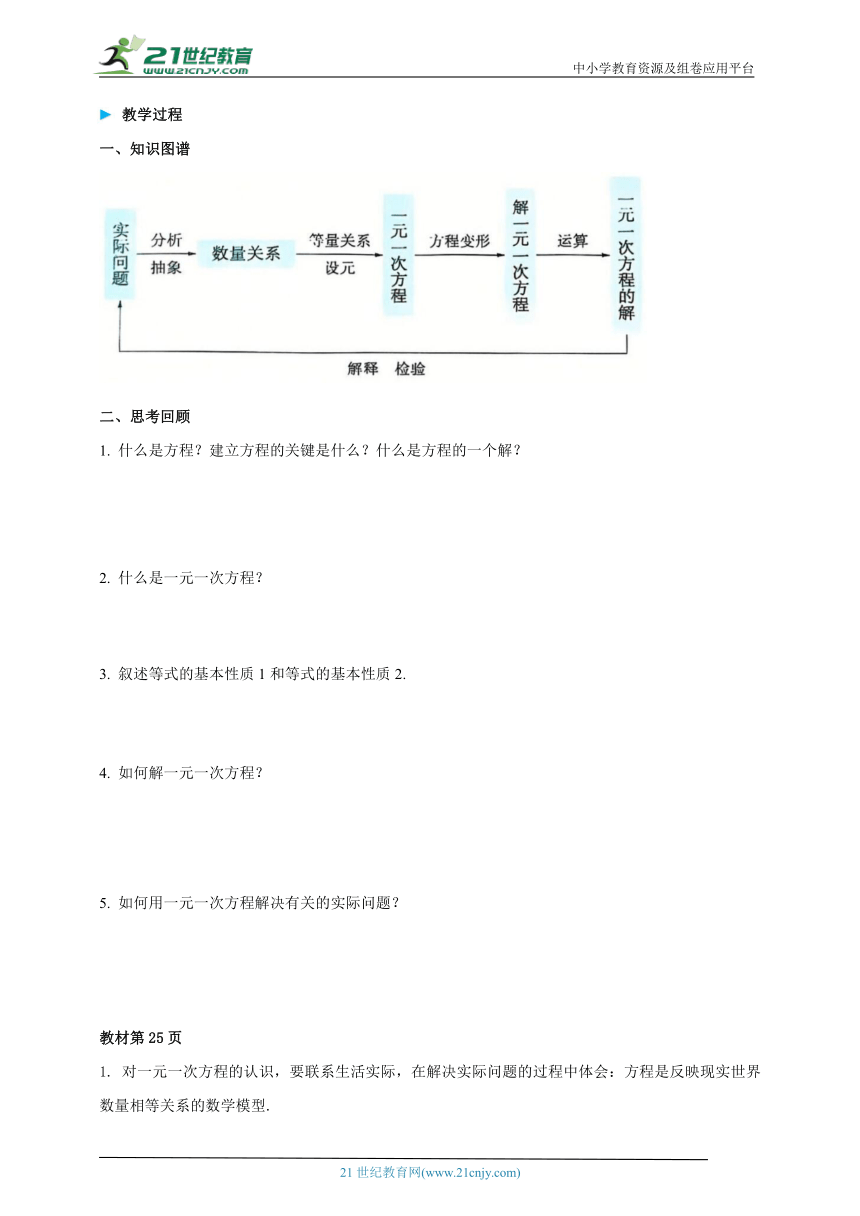
一、知识图谱
二、思考回顾
1. 什么是方程?建立方程的关键是什么?什么是方程的一个解?
2. 什么是一元一次方程?
3. 叙述等式的基本性质1和等式的基本性质2.
4. 如何解一元一次方程?
5. 如何用一元一次方程解决有关的实际问题?
教材第25页
1. 对一元一次方程的认识,要联系生活实际,在解决实际问题的过程中体会:方程是反映现实世界数量相等关系的数学模型.
2. 解一元一次方程时,既要注意合理地对方程进行变形,也要注意根据方程的特点灵活运用方程的变形规则.
3. 在应用一元一次方程解决实际问题时,要学会分析问题的本领. 能根据题意,将实际问题转化为数学问题,特别是要能够寻求主要的等量关系,列出方程. 求得方程的解后,要注意检验所得结果是否符合实际问题的要求.
对于以上问题你还有什么不懂的地方呢?快和同学或者老师讨论一下吧。
三、典例精讲
1.解一元一次方程
(1)-12(x-5)=36
(2)3(20-y)=6y-4(y-10)
(3)
2.有一个方程为,且“□”内是同一个数字,设“□”内数字为x,则该方程为( )
A. B.
C. D.
3.将一笔资金按一年定期存入银行,若年利率为,到期支取时,共得本息和为7140元,则这笔资金是( )
A.6000元 B.6500元 C.7000元 D.7100元
4.20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.求男生有多少人?设男生有x人,则可列方程为( )
A. B.
C. D.
5.若是关于的一元一次方程,则 .
6.若的值与2互为相反数,则x的值为 .
7.某车间有30名工人,生产某种由一个螺栓套两个螺母的产品,每人每天生产螺栓22个或螺母16个.要使每天生产的螺栓和螺母配套,应分配多少名工人生产螺栓?
8.在全民健身运动中,骑行运动颇受市民青睐,甲、乙两骑行爱好者约定从A地沿相同路线骑行去B地,已知甲骑行的速度是乙的1.2倍.若乙先骑行2km,甲才开始从A地出发,则甲出发半小时恰好追上乙,求甲骑行的速度.
【答案】
1.A. 对于 a=b,两边同时减去1,得到 a 1=b 1,所以A选项成立。
B. 对于 a=b,两边同时乘以3,得到 3a=3b,所以B选项成立。
C. 对于 a=b,如果两边同时减去2,应得到 a 2=b 2,而不是 a 2=b+2,所以C选项不成立。
D. 对于 a=b,两边同时除以5,得到 5a =5b ,所以D选项成立。
综上,不成立的选项是C。
2.A. x2 3x=0 是一个等式,且含有未知数x,所以它是方程。
B. 52 x 2 是一个代数式,不是等式,所以它不是方程。
C. 3+( 2)=1 是一个等式,但它不含有未知数,所以它不是方程。
D. 7x>5 是一个不等式,不是等式,所以它不是方程。
综上,是方程的选项是A。
3.将 x=2 代入方程 5x+a=3(x+3),得到:
5×2+a=3×(2+3)
10+a=15
a=5
所以,a的值为5。
4.(1) 解方程 2x+3=4x 9:
移项,得:
2x 4x= 9 3
6x= 12
x=2
(2) 解方程 3(x+2) 2(x+2)=2x+4:
去括号,得:
3x+6 2x 4=2x+4
移项并合并同类项,得:
3x 2x 2x=4 6+4
x=2
x= 2
【典例精析答案】
1.解:(1)
展开左边: 12x+60=36
移项: 12x=36 60
化简: 12x= 24
解得:x= 2
(2)展开60 3y=2y+40
移项:60 40=2y+3y
化简:20=5y
解得:y=4
(3)
去分母:(7x-6)×5-(4x+7)×2=10
去括号:35x-30-8x-14=10
移相:27x=54
解得:x=2
2.解答:D
3. 解答:C
设这笔资金为 x 元。
根据题目,这笔资金按一年定期存入银行,年利率为 2%,到期支取时,共得本息和为 7140 元。
本息和的计算公式是:本息和=本金×(1+年利率),
将题目中的数值代入公式,得到:x×(1+2%)=7140,
化简得:x×1.02=7140,
解这个方程,得到:x=1.027140 =7000,
所以,这笔资金是 7000 元。
故答案为:C. 7000 元。
4.解答:B
5.解答:根据一元一次方程的定义,方程中 x 的最高次数应为 1。
因此,我们有 2k 3=1。
解这个方程,得到 k=2。
6. 解答:根据互为相反数的定义,两数之和为 0。
因此,我们有 2(x 1)+2=0。
去括号,得到 2x 2+2=0。
合并同类项,得到 2x=0。
系数化为 1,得到 x=0。
7. 解:设应分配x名工人生产螺栓,那么剩下的30 x名工人则生产螺母。
每名生产螺栓的工人每天能生产22个螺栓,所以x名工人每天能生产22x个螺栓。
每名生产螺母的工人每天能生产16个螺母,所以30 x名工人每天能生产16(30 x)个螺母。
根据题意,要使每天生产的螺栓和螺母配套,即每天生产的螺母数量是螺栓数量的两倍,可以列出方程:
2×22x=16(30 x),
展开并整理得:
44x=480 16x,
60x=480,
x=8,
所以,应分配8名工人生产螺栓,剩下的30 8=22名工人生产螺母。
答:应分配8名工人生产螺栓。
8.解:设乙骑行的速度为 x 千米/时。
根据题意,甲骑行的速度是乙的 1.2 倍,所以甲骑行的速度为 1.2x 千米/时。
乙先骑行 2 千米,甲才开始从 A 地出发。当甲出发半小时后,即 0.5 小时后,甲恰好追上乙。
在这 0.5 小时内,甲骑行的距离为 1.2x×0.5=0.6x 千米;
乙骑行的距离为 x×0.5=0.5x 千米,但乙之前已经骑行了 2 千米,所以乙总共骑行的距离为 0.5x+2 千米。
由于甲追上乙,所以甲骑行的距离等于乙骑行的总距离,即:
0.6x=0.5x+2,
解这个方程,得到:
0.1x=2,
x=20,
经检验,x=20 是原方程的解,并且符合题意。
因此,甲骑行的速度为 1.2×20=24 千米/时。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章 一元一次方程
小结与复习
学习目标与重难点
学习目标:
理解一元一次方程的概念及其在实际问题中的数学模型作用。
熟练正确解一元一次方程,掌握去括号、去分母、移项等步骤。
3.能够将实际问题抽象为方程,培养分析问题和应用数学解决问题的能力
学习重点:一元一次方程的标准化解法(去分母、去括号、移项等);方程与实际问题的关联性分析;方程解的验算与实际问题匹配性验证
学习难点:从实际问题中抽象出等量关系并正确列出方程;灵活选择方程的变形规则,简化计算过程;解决含多个变量或复杂条件的应用题
复习旧知
1.已知等式,则下列式子中不成立的是( )
A. B. C. D.
2.下列各式中,是方程的是( )
A. B. C. D.
3..若x=2是关于x的方程5x+a=3(x+3)的解,则a的值为 .
4.解下列方程.
(1)-2x+3=4x-9.
(2)3(x+2)-2(x+2)=2x+4.
教学过程
一、知识图谱
二、思考回顾
1. 什么是方程?建立方程的关键是什么?什么是方程的一个解?
2. 什么是一元一次方程?
3. 叙述等式的基本性质1和等式的基本性质2.
4. 如何解一元一次方程?
5. 如何用一元一次方程解决有关的实际问题?
教材第25页
1. 对一元一次方程的认识,要联系生活实际,在解决实际问题的过程中体会:方程是反映现实世界数量相等关系的数学模型.
2. 解一元一次方程时,既要注意合理地对方程进行变形,也要注意根据方程的特点灵活运用方程的变形规则.
3. 在应用一元一次方程解决实际问题时,要学会分析问题的本领. 能根据题意,将实际问题转化为数学问题,特别是要能够寻求主要的等量关系,列出方程. 求得方程的解后,要注意检验所得结果是否符合实际问题的要求.
对于以上问题你还有什么不懂的地方呢?快和同学或者老师讨论一下吧。
三、典例精讲
1.解一元一次方程
(1)-12(x-5)=36
(2)3(20-y)=6y-4(y-10)
(3)
2.有一个方程为,且“□”内是同一个数字,设“□”内数字为x,则该方程为( )
A. B.
C. D.
3.将一笔资金按一年定期存入银行,若年利率为,到期支取时,共得本息和为7140元,则这笔资金是( )
A.6000元 B.6500元 C.7000元 D.7100元
4.20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.求男生有多少人?设男生有x人,则可列方程为( )
A. B.
C. D.
5.若是关于的一元一次方程,则 .
6.若的值与2互为相反数,则x的值为 .
7.某车间有30名工人,生产某种由一个螺栓套两个螺母的产品,每人每天生产螺栓22个或螺母16个.要使每天生产的螺栓和螺母配套,应分配多少名工人生产螺栓?
8.在全民健身运动中,骑行运动颇受市民青睐,甲、乙两骑行爱好者约定从A地沿相同路线骑行去B地,已知甲骑行的速度是乙的1.2倍.若乙先骑行2km,甲才开始从A地出发,则甲出发半小时恰好追上乙,求甲骑行的速度.
【答案】
1.A. 对于 a=b,两边同时减去1,得到 a 1=b 1,所以A选项成立。
B. 对于 a=b,两边同时乘以3,得到 3a=3b,所以B选项成立。
C. 对于 a=b,如果两边同时减去2,应得到 a 2=b 2,而不是 a 2=b+2,所以C选项不成立。
D. 对于 a=b,两边同时除以5,得到 5a =5b ,所以D选项成立。
综上,不成立的选项是C。
2.A. x2 3x=0 是一个等式,且含有未知数x,所以它是方程。
B. 52 x 2 是一个代数式,不是等式,所以它不是方程。
C. 3+( 2)=1 是一个等式,但它不含有未知数,所以它不是方程。
D. 7x>5 是一个不等式,不是等式,所以它不是方程。
综上,是方程的选项是A。
3.将 x=2 代入方程 5x+a=3(x+3),得到:
5×2+a=3×(2+3)
10+a=15
a=5
所以,a的值为5。
4.(1) 解方程 2x+3=4x 9:
移项,得:
2x 4x= 9 3
6x= 12
x=2
(2) 解方程 3(x+2) 2(x+2)=2x+4:
去括号,得:
3x+6 2x 4=2x+4
移项并合并同类项,得:
3x 2x 2x=4 6+4
x=2
x= 2
【典例精析答案】
1.解:(1)
展开左边: 12x+60=36
移项: 12x=36 60
化简: 12x= 24
解得:x= 2
(2)展开60 3y=2y+40
移项:60 40=2y+3y
化简:20=5y
解得:y=4
(3)
去分母:(7x-6)×5-(4x+7)×2=10
去括号:35x-30-8x-14=10
移相:27x=54
解得:x=2
2.解答:D
3. 解答:C
设这笔资金为 x 元。
根据题目,这笔资金按一年定期存入银行,年利率为 2%,到期支取时,共得本息和为 7140 元。
本息和的计算公式是:本息和=本金×(1+年利率),
将题目中的数值代入公式,得到:x×(1+2%)=7140,
化简得:x×1.02=7140,
解这个方程,得到:x=1.027140 =7000,
所以,这笔资金是 7000 元。
故答案为:C. 7000 元。
4.解答:B
5.解答:根据一元一次方程的定义,方程中 x 的最高次数应为 1。
因此,我们有 2k 3=1。
解这个方程,得到 k=2。
6. 解答:根据互为相反数的定义,两数之和为 0。
因此,我们有 2(x 1)+2=0。
去括号,得到 2x 2+2=0。
合并同类项,得到 2x=0。
系数化为 1,得到 x=0。
7. 解:设应分配x名工人生产螺栓,那么剩下的30 x名工人则生产螺母。
每名生产螺栓的工人每天能生产22个螺栓,所以x名工人每天能生产22x个螺栓。
每名生产螺母的工人每天能生产16个螺母,所以30 x名工人每天能生产16(30 x)个螺母。
根据题意,要使每天生产的螺栓和螺母配套,即每天生产的螺母数量是螺栓数量的两倍,可以列出方程:
2×22x=16(30 x),
展开并整理得:
44x=480 16x,
60x=480,
x=8,
所以,应分配8名工人生产螺栓,剩下的30 8=22名工人生产螺母。
答:应分配8名工人生产螺栓。
8.解:设乙骑行的速度为 x 千米/时。
根据题意,甲骑行的速度是乙的 1.2 倍,所以甲骑行的速度为 1.2x 千米/时。
乙先骑行 2 千米,甲才开始从 A 地出发。当甲出发半小时后,即 0.5 小时后,甲恰好追上乙。
在这 0.5 小时内,甲骑行的距离为 1.2x×0.5=0.6x 千米;
乙骑行的距离为 x×0.5=0.5x 千米,但乙之前已经骑行了 2 千米,所以乙总共骑行的距离为 0.5x+2 千米。
由于甲追上乙,所以甲骑行的距离等于乙骑行的总距离,即:
0.6x=0.5x+2,
解这个方程,得到:
0.1x=2,
x=20,
经检验,x=20 是原方程的解,并且符合题意。
因此,甲骑行的速度为 1.2×20=24 千米/时。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
