2025年中考数学九年级【图形的性质】专题(相交线与平行线部分)过关题(含答案)
文档属性
| 名称 | 2025年中考数学九年级【图形的性质】专题(相交线与平行线部分)过关题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 335.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 14:37:34 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年中考数学
九年级【图形的性质】专题(相交线与平行线)部分过关题
一、单选题
1.(2024九下·乐陵期中)将一副直角三角板按如图所示的方式叠放在一起,若,则的度数为( )
A. B. C. D.
2.(2023九下·九龙坡月考)如图,直线,直线分别交直线于点E, F,若,则的度数为( )
A. B. C. D.
3.(2024九下·西宁模拟)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面与平行,入射光线l与出射光线m平行.若入射光线l与镜面的夹角,则的度数为( )
A. B. C. D.
4.如图,a∥b,∠1=∠2,∠3=40°,则∠4等于( )
A.40° B.50° C.60° D.70°
5.(2021·武进模拟)如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=44°时, 的大小为( )
A. B. C. D.
6.如图 , 斑马线的作用是为了引导行人安全地通过马路. 小丽觉得行人沿垂直马路的方向走过斑马线更为合理, 这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
7.(2019七下·蔡甸月考)如图,CD//AB,AC⊥BC,∠ACD=60°,那么∠B的度数是( )
A.60° B.40° C.45° D.30°
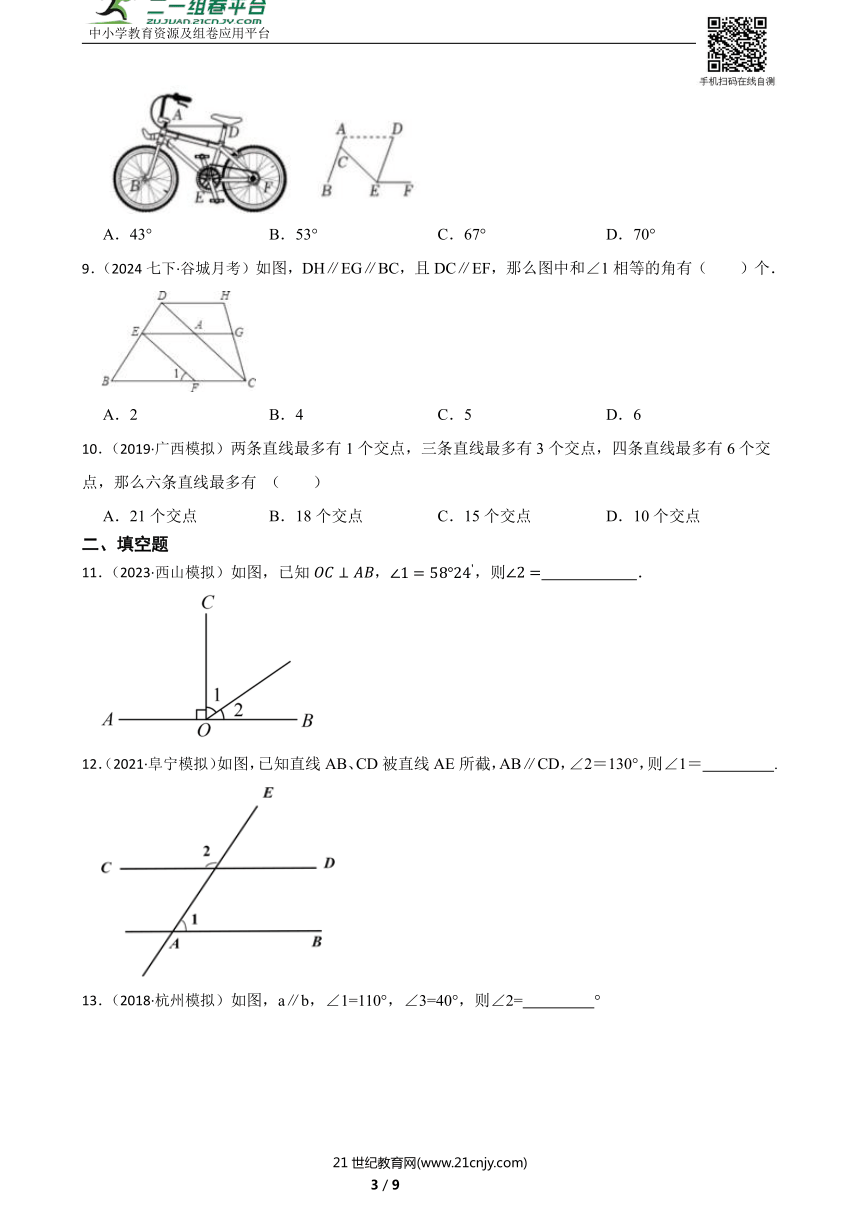
8.(2024九下·武昌月考)随着科技发展,骑行共享单车这种“低碳”生活方式已融入人们的日常生活,如图是线段AB,CE,DE分别为前叉、下管和立管(点C在AB上),EF为后下叉.已知AB∥DE,AD∥EF,,则的度数为( )
A.43° B.53° C.67° D.70°
9.(2024七下·谷城月考)如图,DH∥EG∥BC,且DC∥EF,那么图中和∠1相等的角有( )个.
A.2 B.4 C.5 D.6
10.(2019·广西模拟)两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点,那么六条直线最多有 ( )
A.21个交点 B.18个交点 C.15个交点 D.10个交点
二、填空题
11.(2023·西山模拟)如图,已知,,则 .
12.(2021·阜宁模拟)如图,已知直线AB、CD被直线AE所截,AB∥CD,∠2=130°,则∠1= .
13.(2018·杭州模拟)如图,a∥b,∠1=110°,∠3=40°,则∠2= °
14.(2019九上·万州期末)已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
解:∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∵∠ACD=∠ (已作)
AB∥CD( )
∴∠B= ( )
而∠ACB+∠ACD+∠DCE=180°
∴∠ACB+ + =180°( )
15.(2023·凤凰模拟)如图,直线AB//CD,,,则 .
16.(2021·阳谷模拟)如图,直线l1∥l2,∠BAE=125°,∠ABF=85°,则∠1+∠2= .
三、计算题
17.(2024七上·武汉月考)图①为北斗七星的位置图,图②将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=∠E=105°.
(1)求∠F的度数;
(2)计算∠B-∠CGF的度数是______;(直接写出结果)
(3)连接AD,∠ADE与∠CGF满足怎样数量关系时,BC∥AD,并说明理由.
四、解答题
18.(2021八上·佛山月考)如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
19.(2023·新城模拟)如图所示,,相交于点O,,,与平行吗?为什么?
20.(2023九上·盘锦开学考)如图,EF∥AD,∠1=∠2,求∠AGD的度数.请将解题过程填写完整.
解:∵EF∥AD(已知),
∴∠2= ▲ ( ),
又∵∠1=∠2(已知),
∴∠1=∠3( ),
∴AB∥ ▲ ( ),
∴∠BAC+ ▲ =180°( ),
∵∠BAC=70°(已知),
∴∠AGD= ▲ .
21.如图1,已知AB//CD,E,F分别是AB,CD上的点,P为AB,CD之间的一点,且始终在直线EF的左侧,连结EP,PF.
(1)求证: ∠AEP+∠CFP=∠EPF.
(2)如图2,在AB,CD内部另作一条折线E—Q—F,且点Q在直线EF的右侧.
①若∠BEP = 2∠BEQ,∠DFP =2∠DFQ, ∠EQF=130°,求∠EPF的度数.
②若∠BEP=n∠BEQ, ∠DFP=n∠DFQ,请直接写出∠EPF与∠EQF之间的数量关系(用含n的代数式表示).
答案解析部分
1.【答案】C
【知识点】平行线的性质
2.【答案】D
【知识点】内错角的概念
3.【答案】C
【知识点】内错角的概念
4.【答案】D
【知识点】平行线的性质
5.【答案】B
【知识点】平行线的性质
6.【答案】A
【知识点】垂线段最短及其应用
7.【答案】D
【知识点】垂线的概念;平行线的性质
8.【答案】D
【知识点】平行线的判定与性质的应用-求角度
9.【答案】C
【知识点】平行线的性质
10.【答案】C
【知识点】相交线的相关概念
11.【答案】
【知识点】余角、补角及其性质;垂线的概念
12.【答案】50°
【知识点】平行线的性质;邻补角
13.【答案】70
【知识点】平行线的性质;对顶角及其性质
14.【答案】A;内错角相等,两直线平行;∠DCE;两直线平行,同位角相等;∠A;∠B;等量代换
【知识点】平行线的判定与性质
15.【答案】135°
【知识点】平行公理及推论;平行线的性质
16.【答案】30°
【知识点】平行线的判定与性质
17.【答案】(1)75°(2)115°(3)当∠ADE+∠CGF=180°时,BC∥AD
【知识点】平行线的判定与性质
18.【答案】解:∵EF∥GH,
∴∠ABD+∠FAC=180°,
∴∠ABD=180°﹣72°=108°,
∵∠ABD=∠ACD+∠BDC,
∴∠BDC=∠ABD﹣∠ACD=108°﹣58°=50°.
【知识点】平行线的性质
19.【答案】解:,理由如下:∵,,,
∴,
∴.
【知识点】平行线的判定;对顶角及其性质
20.【答案】解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等),
又∵∠5=∠2(已知),
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=70°(已知),
∴∠AGD=110°.
故答案为:∠3;两直线平行;等量代换,内错角相等;∠AGD,同旁内角互补.
【知识点】平行线的性质
21.【答案】(1)证明:如图1,
过点P作PG∥AB,
∵AB∥CD,
∴PG∥CD,
∴∠AEP=∠1,∠CFP=∠2,
又∵∠1+∠2=∠EPF,
∴∠AEP+∠CFP=∠EPF;
(2)解:①如图2,
由(1)可得∠EPF=∠AEP+∠CFP,∠EQF=∠BEQ+∠DFQ,
∵∠BEP=2∠BEQ,∠DFQ=2∠DFP,
∴∠BEQ∠BEP,∠DFP∠DFQ,
∴∠EQF=∠BEQ+∠DFQ(∠BEP+∠DFP)[360°﹣(∠AEP+∠CFP)](360°﹣∠EPF),
∴∠EPF+2∠EQF=360°.
∴∠EPF=360°-2∠EQF=360°-2×130°=100°.
②由(1),可得∠EPF=∠AEP+∠CFP,∠EQF=∠BEQ+∠DFQ,
∵∠BEQ=n∠BEP,∠DFQ=n∠DFP,
∴∠BEQ∠BEP,∠DFP∠DFQ,
∴∠EQF=∠BEQ+∠DFQ(∠BEP+∠DFP)[360°﹣(∠AEP+∠CFP)](360°﹣∠EPF),
∴∠EPF+n∠EQF=360°.
∴∠EPF=360°-n∠EQF.
【知识点】平行公理及推论;平行线的性质;平行线的判定与性质
21世纪教育网(www.21cnjy.com)
1 / 9
2025年中考数学
九年级【图形的性质】专题(相交线与平行线)部分过关题
一、单选题
1.(2024九下·乐陵期中)将一副直角三角板按如图所示的方式叠放在一起,若,则的度数为( )
A. B. C. D.
2.(2023九下·九龙坡月考)如图,直线,直线分别交直线于点E, F,若,则的度数为( )
A. B. C. D.
3.(2024九下·西宁模拟)如图是小亮绘制的潜望镜原理示意图,两个平面镜的镜面与平行,入射光线l与出射光线m平行.若入射光线l与镜面的夹角,则的度数为( )
A. B. C. D.
4.如图,a∥b,∠1=∠2,∠3=40°,则∠4等于( )
A.40° B.50° C.60° D.70°
5.(2021·武进模拟)如图,将一块三角板的直角顶点放在直尺的一边上,当∠2=44°时, 的大小为( )
A. B. C. D.
6.如图 , 斑马线的作用是为了引导行人安全地通过马路. 小丽觉得行人沿垂直马路的方向走过斑马线更为合理, 这一想法体现的数学依据是( )
A.垂线段最短
B.两点确定一条直线
C.过一点有且只有一条直线与已知直线垂直
D.过直线外一点有且只有一条直线与已知直线平行
7.(2019七下·蔡甸月考)如图,CD//AB,AC⊥BC,∠ACD=60°,那么∠B的度数是( )
A.60° B.40° C.45° D.30°
8.(2024九下·武昌月考)随着科技发展,骑行共享单车这种“低碳”生活方式已融入人们的日常生活,如图是线段AB,CE,DE分别为前叉、下管和立管(点C在AB上),EF为后下叉.已知AB∥DE,AD∥EF,,则的度数为( )
A.43° B.53° C.67° D.70°
9.(2024七下·谷城月考)如图,DH∥EG∥BC,且DC∥EF,那么图中和∠1相等的角有( )个.
A.2 B.4 C.5 D.6
10.(2019·广西模拟)两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点,那么六条直线最多有 ( )
A.21个交点 B.18个交点 C.15个交点 D.10个交点
二、填空题
11.(2023·西山模拟)如图,已知,,则 .
12.(2021·阜宁模拟)如图,已知直线AB、CD被直线AE所截,AB∥CD,∠2=130°,则∠1= .
13.(2018·杭州模拟)如图,a∥b,∠1=110°,∠3=40°,则∠2= °
14.(2019九上·万州期末)已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
解:∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∵∠ACD=∠ (已作)
AB∥CD( )
∴∠B= ( )
而∠ACB+∠ACD+∠DCE=180°
∴∠ACB+ + =180°( )
15.(2023·凤凰模拟)如图,直线AB//CD,,,则 .
16.(2021·阳谷模拟)如图,直线l1∥l2,∠BAE=125°,∠ABF=85°,则∠1+∠2= .
三、计算题
17.(2024七上·武汉月考)图①为北斗七星的位置图,图②将北斗七星分别标为A,B,C,D,E,F,G,将A,B,C,D,E,F顺次首尾连接,若AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=∠E=105°.
(1)求∠F的度数;
(2)计算∠B-∠CGF的度数是______;(直接写出结果)
(3)连接AD,∠ADE与∠CGF满足怎样数量关系时,BC∥AD,并说明理由.
四、解答题
18.(2021八上·佛山月考)如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
19.(2023·新城模拟)如图所示,,相交于点O,,,与平行吗?为什么?
20.(2023九上·盘锦开学考)如图,EF∥AD,∠1=∠2,求∠AGD的度数.请将解题过程填写完整.
解:∵EF∥AD(已知),
∴∠2= ▲ ( ),
又∵∠1=∠2(已知),
∴∠1=∠3( ),
∴AB∥ ▲ ( ),
∴∠BAC+ ▲ =180°( ),
∵∠BAC=70°(已知),
∴∠AGD= ▲ .
21.如图1,已知AB//CD,E,F分别是AB,CD上的点,P为AB,CD之间的一点,且始终在直线EF的左侧,连结EP,PF.
(1)求证: ∠AEP+∠CFP=∠EPF.
(2)如图2,在AB,CD内部另作一条折线E—Q—F,且点Q在直线EF的右侧.
①若∠BEP = 2∠BEQ,∠DFP =2∠DFQ, ∠EQF=130°,求∠EPF的度数.
②若∠BEP=n∠BEQ, ∠DFP=n∠DFQ,请直接写出∠EPF与∠EQF之间的数量关系(用含n的代数式表示).
答案解析部分
1.【答案】C
【知识点】平行线的性质
2.【答案】D
【知识点】内错角的概念
3.【答案】C
【知识点】内错角的概念
4.【答案】D
【知识点】平行线的性质
5.【答案】B
【知识点】平行线的性质
6.【答案】A
【知识点】垂线段最短及其应用
7.【答案】D
【知识点】垂线的概念;平行线的性质
8.【答案】D
【知识点】平行线的判定与性质的应用-求角度
9.【答案】C
【知识点】平行线的性质
10.【答案】C
【知识点】相交线的相关概念
11.【答案】
【知识点】余角、补角及其性质;垂线的概念
12.【答案】50°
【知识点】平行线的性质;邻补角
13.【答案】70
【知识点】平行线的性质;对顶角及其性质
14.【答案】A;内错角相等,两直线平行;∠DCE;两直线平行,同位角相等;∠A;∠B;等量代换
【知识点】平行线的判定与性质
15.【答案】135°
【知识点】平行公理及推论;平行线的性质
16.【答案】30°
【知识点】平行线的判定与性质
17.【答案】(1)75°(2)115°(3)当∠ADE+∠CGF=180°时,BC∥AD
【知识点】平行线的判定与性质
18.【答案】解:∵EF∥GH,
∴∠ABD+∠FAC=180°,
∴∠ABD=180°﹣72°=108°,
∵∠ABD=∠ACD+∠BDC,
∴∠BDC=∠ABD﹣∠ACD=108°﹣58°=50°.
【知识点】平行线的性质
19.【答案】解:,理由如下:∵,,,
∴,
∴.
【知识点】平行线的判定;对顶角及其性质
20.【答案】解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等),
又∵∠5=∠2(已知),
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=70°(已知),
∴∠AGD=110°.
故答案为:∠3;两直线平行;等量代换,内错角相等;∠AGD,同旁内角互补.
【知识点】平行线的性质
21.【答案】(1)证明:如图1,
过点P作PG∥AB,
∵AB∥CD,
∴PG∥CD,
∴∠AEP=∠1,∠CFP=∠2,
又∵∠1+∠2=∠EPF,
∴∠AEP+∠CFP=∠EPF;
(2)解:①如图2,
由(1)可得∠EPF=∠AEP+∠CFP,∠EQF=∠BEQ+∠DFQ,
∵∠BEP=2∠BEQ,∠DFQ=2∠DFP,
∴∠BEQ∠BEP,∠DFP∠DFQ,
∴∠EQF=∠BEQ+∠DFQ(∠BEP+∠DFP)[360°﹣(∠AEP+∠CFP)](360°﹣∠EPF),
∴∠EPF+2∠EQF=360°.
∴∠EPF=360°-2∠EQF=360°-2×130°=100°.
②由(1),可得∠EPF=∠AEP+∠CFP,∠EQF=∠BEQ+∠DFQ,
∵∠BEQ=n∠BEP,∠DFQ=n∠DFP,
∴∠BEQ∠BEP,∠DFP∠DFQ,
∴∠EQF=∠BEQ+∠DFQ(∠BEP+∠DFP)[360°﹣(∠AEP+∠CFP)](360°﹣∠EPF),
∴∠EPF+n∠EQF=360°.
∴∠EPF=360°-n∠EQF.
【知识点】平行公理及推论;平行线的性质;平行线的判定与性质
21世纪教育网(www.21cnjy.com)
1 / 9
同课章节目录
