2025年中考数学九年级一轮复习【图形的性质】专题(三角形)部分过关题(含答案)
文档属性
| 名称 | 2025年中考数学九年级一轮复习【图形的性质】专题(三角形)部分过关题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 330.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 18:02:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年中考数学九年级
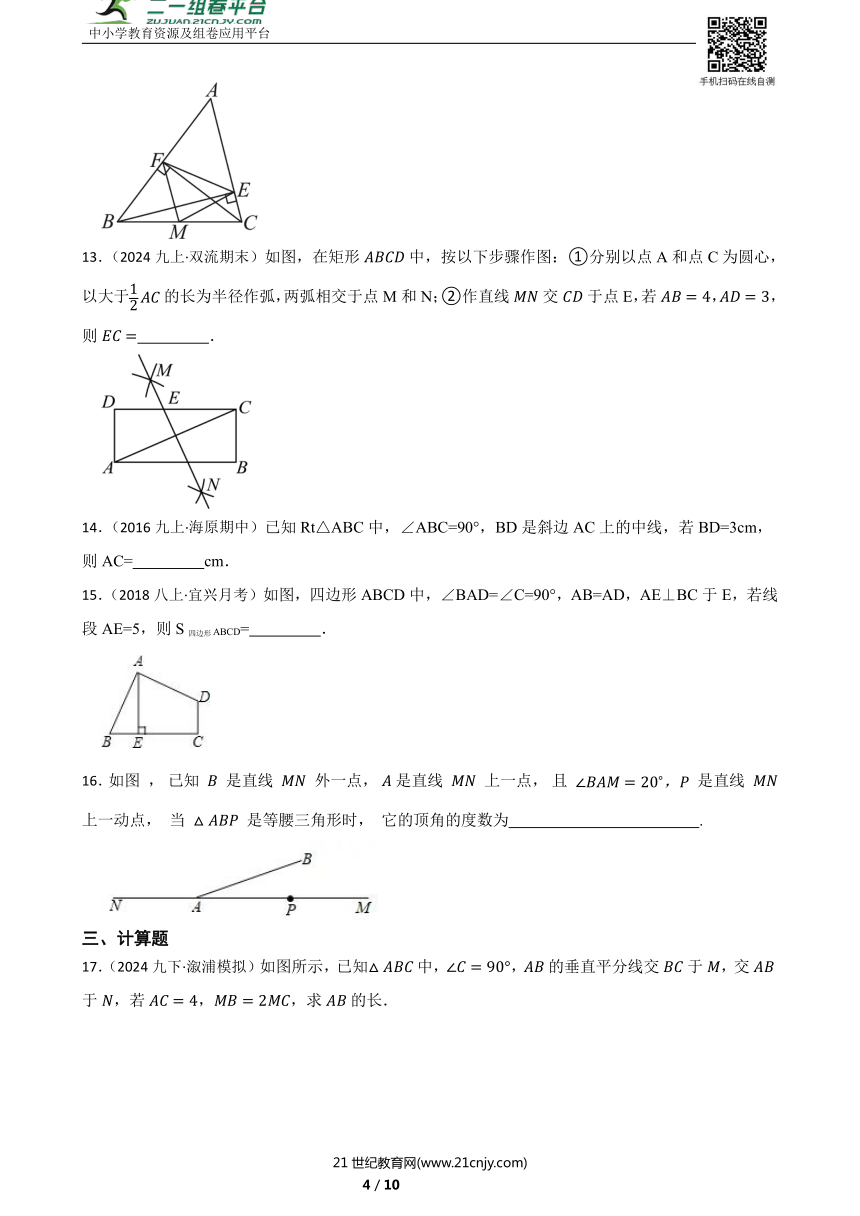
一轮复习【图形的性质】专题(三角形)部分过关题
一、单选题
1.(2024九下·凉州模拟)如图,是等边三角形,D、E分别是的边、上的点,且,与相交于点P,于点F,,,则的长为( )
A.8 B.13 C.16 D.17
2.(2018·江城模拟)已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是( )
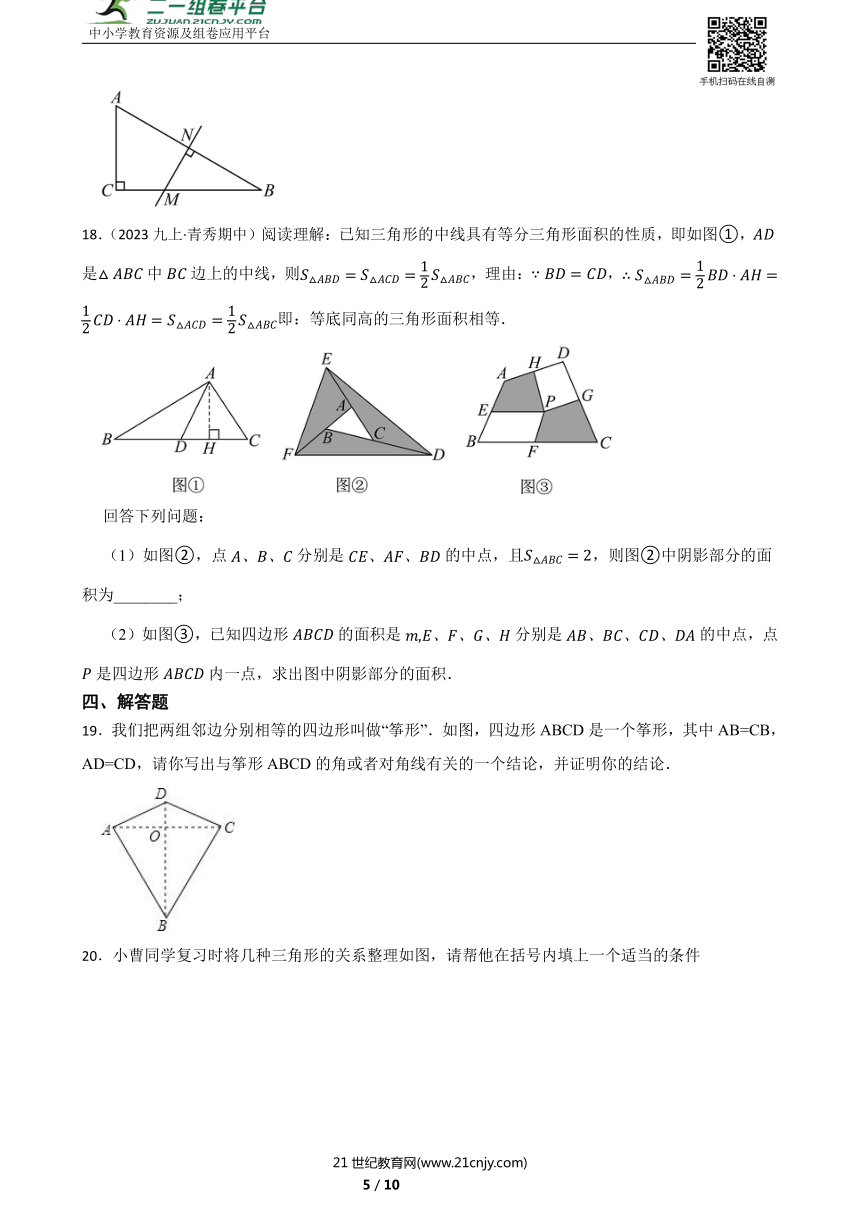
A.8 B.7 C.4 D.3
3.(2023九上·贵阳月考)已知在中,,,在延长线上且,则的度数( )
A. B. C. D.
4.(2024九下·十堰模拟)小明在数学课上,将文具盒中的直角三角板与一直尺放置如图,若测得∠AEF=50°,那么∠BDA= ( )
A.20° B.40° C.50° D.60°
5.(2024九下·温江模拟)如图,在 和 中,点 在同一直线上,,,请添加一个条件,使 ,这个条件可以是( )
A. B. C. D.
6.(2018九上·武昌期中)如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路 上 处距 点 米.如果火车行驶时,周围 米以内会受到噪音的影响.那么火车在铁路 上沿 方向以 千米/时的速度行驶时, 处受噪音影响的时间为( )
A. 秒 B. 秒 C. 秒 D. 秒
7.(2017·荆州)如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )
A.30° B.45° C.50° D.75°
8.(2023八上·哈尔滨月考)如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于 BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( )
A.2 B.3 C.4 D.6
9.(2016·余姚模拟)说明命题“等腰三角形腰上的高小于腰”是假命题的反例可以是( )
A.等腰直角三角形 B.等边三角形
C.含30°的直角三角形 D.顶角为45°的等腰三角形
10.(2023九上·金平期中)如图,是的角平分线,;垂足为交的延长线于点,若恰好平分.给出下列三个结论:①;②;③.其中正确的结论共有( )个
A. B. C. D.
二、填空题
11.(2020·山西模拟)如图,在△ABC中,AC=BC,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,连接MN分别交BC、AC于点D、E,连接AD.若∠B=70°,则∠BAD的度数是 度.
12.(2024九下·立山期中)如图,、分别是的高,为的中点,,,则的周长是 .
13.(2024九上·双流期末)如图,在矩形中,按以下步骤作图:①分别以点A和点C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②作直线交于点E,若,,则 .
14.(2016九上·海原期中)已知Rt△ABC中,∠ABC=90°,BD是斜边AC上的中线,若BD=3cm,则AC= cm.
15.(2018八上·宜兴月考)如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC于E,若线段AE=5,则S四边形ABCD= .
16.如图 , 已知 是直线 外一点, 是直线 上一点, 且 是直线 上一动点, 当 是等腰三角形时, 它的顶角的度数为 .
三、计算题
17.(2024九下·溆浦模拟)如图所示,已知中,,的垂直平分线交于,交于,若,,求的长.
18.(2023九上·青秀期中)阅读理解:已知三角形的中线具有等分三角形面积的性质,即如图①,是中边上的中线,则,理由:,即:等底同高的三角形面积相等.
回答下列问题:
(1)如图②,点分别是的中点,且,则图②中阴影部分的面积为________;
(2)如图③,已知四边形的面积是分别是的中点,点是四边形内一点,求出图中阴影部分的面积.
四、解答题
19.我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,请你写出与筝形ABCD的角或者对角线有关的一个结论,并证明你的结论.
20.小曹同学复习时将几种三角形的关系整理如图,请帮他在括号内填上一个适当的条件
21.如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段DE,点A、B、D、E均在小正方形的顶点上.
(1)在方格纸中画出以AB为一边的直角三角形ABC,点C在小正方形的顶点上,且三角形ABC的面积为.
(2)在方格纸中画出以DE为一边、一个内角为钝角的等腰三角形DEF,点F在小正方形的顶点上,且三角形DEF的面积为4.连接CF,请直接写出线段CF的长.
22.(2024九上·广州月考)如图,在平面直角坐标系中,抛物线的顶点坐标为,并与y轴交于点,点A是对称轴与x轴的交点.
(1)求抛物线的解析式;
(2)如图①所示,P是抛物线上的一个动点,且位于第一象限,连接,,求的面积的最大值;
(3)如图②所示,在对称轴右侧的抛物线上是否存在一点D,使,如果存在,求出D点的坐标;如果不存在,请说明理由
答案解析部分
1.【答案】B
【知识点】等边三角形的性质;含30°角的直角三角形;三角形全等的判定-SAS
2.【答案】B
【知识点】三角形三边关系;等腰三角形的性质
3.【答案】B
【知识点】等腰三角形的判定与性质;三角形全等的判定-SAS
4.【答案】A
【知识点】三角形的外角性质
5.【答案】C
【知识点】三角形全等的判定
6.【答案】B
【知识点】勾股定理的应用
7.【答案】B
【知识点】线段垂直平分线的性质;等腰三角形的性质
8.【答案】C
【知识点】线段垂直平分线的性质
9.【答案】A
【知识点】等腰三角形的性质
10.【答案】D
【知识点】三角形全等及其性质
11.【答案】30
【知识点】线段垂直平分线的性质
12.【答案】13
【知识点】直角三角形斜边上的中线
13.【答案】
【知识点】线段垂直平分线的性质;勾股定理
14.【答案】6
【知识点】直角三角形斜边上的中线
15.【答案】25
【知识点】全等三角形的判定与性质
16.【答案】 或 或
【知识点】等腰三角形的性质;等腰三角形的判定
17.【答案】8
【知识点】线段垂直平分线的性质;勾股定理
18.【答案】(1)12
(2)(2)
连接,
∵是边的中点,
∴,
同理,
∴图中阴影部分的面积四边形的面积.
【知识点】三角形的角平分线、中线和高;三角形的面积
19.【答案】解:AC⊥BD,理由为:
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SSS),
∴∠ABO=∠CBO,
∵AB=CB,
∴BD⊥AC.
【知识点】全等三角形的判定与性质
20.【答案】解:(答案不唯一).
【知识点】等边三角形的判定
21.【答案】解:(1)如图:
(2)如图,CF=.
【知识点】勾股定理
22.【答案】(1);(2);(3)存在,
【知识点】含30°角的直角三角形;勾股定理
21世纪教育网(www.21cnjy.com)
2 / 10
2025年中考数学九年级
一轮复习【图形的性质】专题(三角形)部分过关题
一、单选题
1.(2024九下·凉州模拟)如图,是等边三角形,D、E分别是的边、上的点,且,与相交于点P,于点F,,,则的长为( )
A.8 B.13 C.16 D.17
2.(2018·江城模拟)已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是( )
A.8 B.7 C.4 D.3
3.(2023九上·贵阳月考)已知在中,,,在延长线上且,则的度数( )
A. B. C. D.
4.(2024九下·十堰模拟)小明在数学课上,将文具盒中的直角三角板与一直尺放置如图,若测得∠AEF=50°,那么∠BDA= ( )
A.20° B.40° C.50° D.60°
5.(2024九下·温江模拟)如图,在 和 中,点 在同一直线上,,,请添加一个条件,使 ,这个条件可以是( )
A. B. C. D.
6.(2018九上·武昌期中)如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路 上 处距 点 米.如果火车行驶时,周围 米以内会受到噪音的影响.那么火车在铁路 上沿 方向以 千米/时的速度行驶时, 处受噪音影响的时间为( )
A. 秒 B. 秒 C. 秒 D. 秒
7.(2017·荆州)如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )
A.30° B.45° C.50° D.75°
8.(2023八上·哈尔滨月考)如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于 BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为( )
A.2 B.3 C.4 D.6
9.(2016·余姚模拟)说明命题“等腰三角形腰上的高小于腰”是假命题的反例可以是( )
A.等腰直角三角形 B.等边三角形
C.含30°的直角三角形 D.顶角为45°的等腰三角形
10.(2023九上·金平期中)如图,是的角平分线,;垂足为交的延长线于点,若恰好平分.给出下列三个结论:①;②;③.其中正确的结论共有( )个
A. B. C. D.
二、填空题
11.(2020·山西模拟)如图,在△ABC中,AC=BC,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,连接MN分别交BC、AC于点D、E,连接AD.若∠B=70°,则∠BAD的度数是 度.
12.(2024九下·立山期中)如图,、分别是的高,为的中点,,,则的周长是 .
13.(2024九上·双流期末)如图,在矩形中,按以下步骤作图:①分别以点A和点C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②作直线交于点E,若,,则 .
14.(2016九上·海原期中)已知Rt△ABC中,∠ABC=90°,BD是斜边AC上的中线,若BD=3cm,则AC= cm.
15.(2018八上·宜兴月考)如图,四边形ABCD中,∠BAD=∠C=90°,AB=AD,AE⊥BC于E,若线段AE=5,则S四边形ABCD= .
16.如图 , 已知 是直线 外一点, 是直线 上一点, 且 是直线 上一动点, 当 是等腰三角形时, 它的顶角的度数为 .
三、计算题
17.(2024九下·溆浦模拟)如图所示,已知中,,的垂直平分线交于,交于,若,,求的长.
18.(2023九上·青秀期中)阅读理解:已知三角形的中线具有等分三角形面积的性质,即如图①,是中边上的中线,则,理由:,即:等底同高的三角形面积相等.
回答下列问题:
(1)如图②,点分别是的中点,且,则图②中阴影部分的面积为________;
(2)如图③,已知四边形的面积是分别是的中点,点是四边形内一点,求出图中阴影部分的面积.
四、解答题
19.我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD,请你写出与筝形ABCD的角或者对角线有关的一个结论,并证明你的结论.
20.小曹同学复习时将几种三角形的关系整理如图,请帮他在括号内填上一个适当的条件
21.如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段DE,点A、B、D、E均在小正方形的顶点上.
(1)在方格纸中画出以AB为一边的直角三角形ABC,点C在小正方形的顶点上,且三角形ABC的面积为.
(2)在方格纸中画出以DE为一边、一个内角为钝角的等腰三角形DEF,点F在小正方形的顶点上,且三角形DEF的面积为4.连接CF,请直接写出线段CF的长.
22.(2024九上·广州月考)如图,在平面直角坐标系中,抛物线的顶点坐标为,并与y轴交于点,点A是对称轴与x轴的交点.
(1)求抛物线的解析式;
(2)如图①所示,P是抛物线上的一个动点,且位于第一象限,连接,,求的面积的最大值;
(3)如图②所示,在对称轴右侧的抛物线上是否存在一点D,使,如果存在,求出D点的坐标;如果不存在,请说明理由
答案解析部分
1.【答案】B
【知识点】等边三角形的性质;含30°角的直角三角形;三角形全等的判定-SAS
2.【答案】B
【知识点】三角形三边关系;等腰三角形的性质
3.【答案】B
【知识点】等腰三角形的判定与性质;三角形全等的判定-SAS
4.【答案】A
【知识点】三角形的外角性质
5.【答案】C
【知识点】三角形全等的判定
6.【答案】B
【知识点】勾股定理的应用
7.【答案】B
【知识点】线段垂直平分线的性质;等腰三角形的性质
8.【答案】C
【知识点】线段垂直平分线的性质
9.【答案】A
【知识点】等腰三角形的性质
10.【答案】D
【知识点】三角形全等及其性质
11.【答案】30
【知识点】线段垂直平分线的性质
12.【答案】13
【知识点】直角三角形斜边上的中线
13.【答案】
【知识点】线段垂直平分线的性质;勾股定理
14.【答案】6
【知识点】直角三角形斜边上的中线
15.【答案】25
【知识点】全等三角形的判定与性质
16.【答案】 或 或
【知识点】等腰三角形的性质;等腰三角形的判定
17.【答案】8
【知识点】线段垂直平分线的性质;勾股定理
18.【答案】(1)12
(2)(2)
连接,
∵是边的中点,
∴,
同理,
∴图中阴影部分的面积四边形的面积.
【知识点】三角形的角平分线、中线和高;三角形的面积
19.【答案】解:AC⊥BD,理由为:
在△ABD和△CBD中,
,
∴△ABD≌△CBD(SSS),
∴∠ABO=∠CBO,
∵AB=CB,
∴BD⊥AC.
【知识点】全等三角形的判定与性质
20.【答案】解:(答案不唯一).
【知识点】等边三角形的判定
21.【答案】解:(1)如图:
(2)如图,CF=.
【知识点】勾股定理
22.【答案】(1);(2);(3)存在,
【知识点】含30°角的直角三角形;勾股定理
21世纪教育网(www.21cnjy.com)
2 / 10
同课章节目录
