2025年中考数学九年级一轮复习【图形的性质】专题(四边形)部分过关题(含答案)
文档属性
| 名称 | 2025年中考数学九年级一轮复习【图形的性质】专题(四边形)部分过关题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 360.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 16:21:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年中考数学九年级
一轮复习【图形的性质】专题(四边形)部分过关题
一、单选题
1.(2023九上·福田期中)已知菱形 的对角线 , 的长度分别为8 和6 ,则菱形 的周长是( )
A.10 B.16 C.20 D.40
2.(2024八下·凉州期中)正方形具有而菱形不具有的性质是( )
A.对角相等 B.对角线互相平分
C.对角线相等 D.四条边都相等
3.(2023·大渡口模拟)矩形中,,,则的长为( )
A.5 B.4 C.3 D.2
4.(2024九下·怀化模拟)如图,△ABC边AB,BC,AC上的中点分别是D,E,F,且各边的长度分别为5厘米,4厘米,6厘米,则四边形ADEF的周长是( )
A.9厘米 B.10厘米 C.11厘米 D.12厘米
5.(2024九下·罗湖模拟)如图,已知平行四边形的面积为,为的中点,连接,则的面积为( )
A. B. C. D.
6.(2024八下·崇义期中)如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:
① .四边形EFGH一定是平行四边形;
②.若AC=BD,则四边形EFGH 是菱形;
③.若AC⊥BD,则四边形EFGH是矩形.
其中正确的是( )
A.① B.①② C.①③ D.①②③
7.(2024九上·柳南月考)如图,在菱形中,、分别是、的中点,如果,那么菱形的周长是( )
A.16 B.8 C.4 D.2
8.如图,沿Rt△ABC的中位线DE剪切一刀后,用得到的△ADE和四边形DBCE拼图,下列图形:①平行四边形;②菱形;③矩形;④等腰梯形.一定能拼出的是( )
A.只有①② B.只有③④ C.只有①③④ D.①②③④
9.(2024·宁海)如图四边形与是并列放在一起的两个正方形,是与的交点.如果正方形的面积是9,,则的面积为
A.1 B. C.4 D.
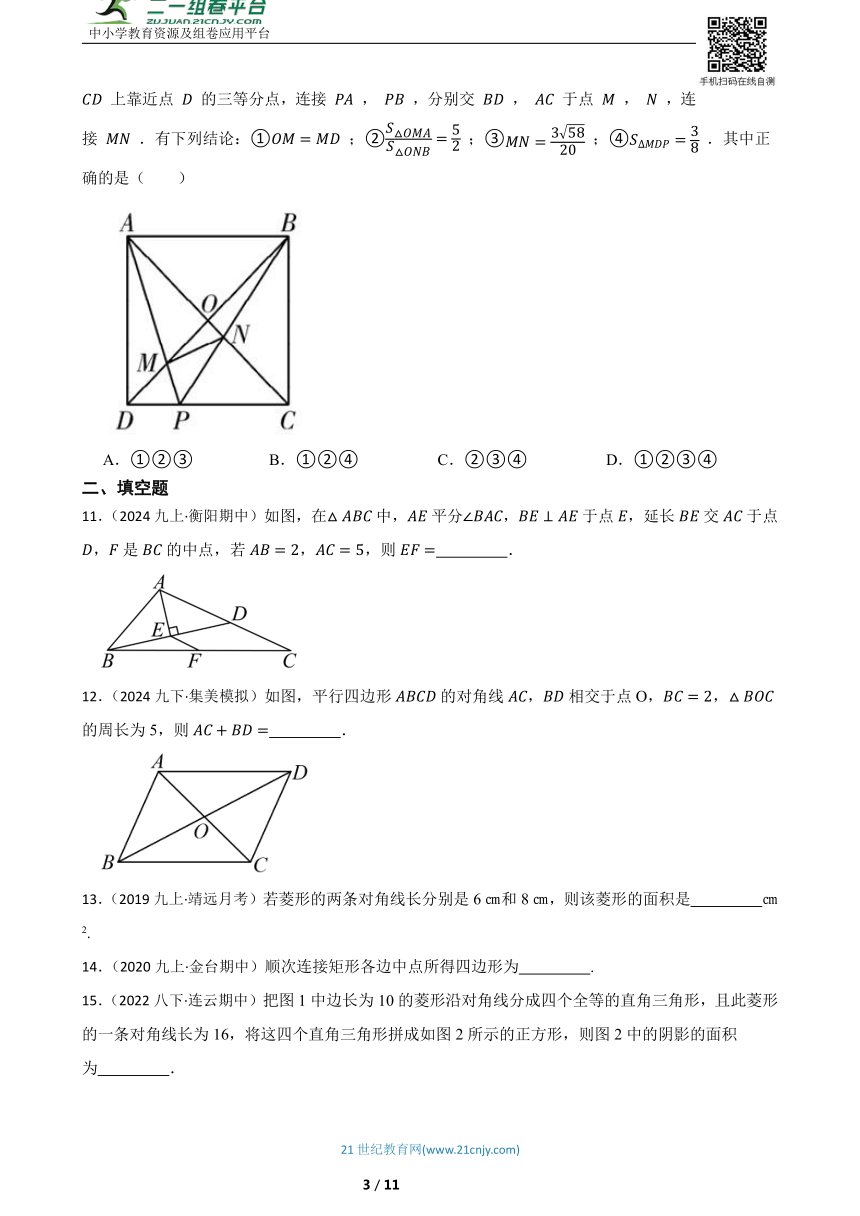
10.(2021·惠城模拟)如图,正方形 的边 ,对角线 和 交于点 , 是边 上靠近点 的三等分点,连接 , ,分别交 , 于点 , ,连接 .有下列结论:① ;② ;③ ;④ .其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题
11.(2024九上·衡阳期中)如图,在中,平分,于点,延长交于点,是的中点,若,,则 .
12.(2024九下·集美模拟)如图,平行四边形的对角线,相交于点O,,的周长为5,则 .
13.(2019九上·靖远月考)若菱形的两条对角线长分别是6㎝和8㎝,则该菱形的面积是 ㎝2.
14.(2020九上·金台期中)顺次连接矩形各边中点所得四边形为 .
15.(2022八下·连云期中)把图1中边长为10的菱形沿对角线分成四个全等的直角三角形,且此菱形的一条对角线长为16,将这四个直角三角形拼成如图2所示的正方形,则图2中的阴影的面积为 .
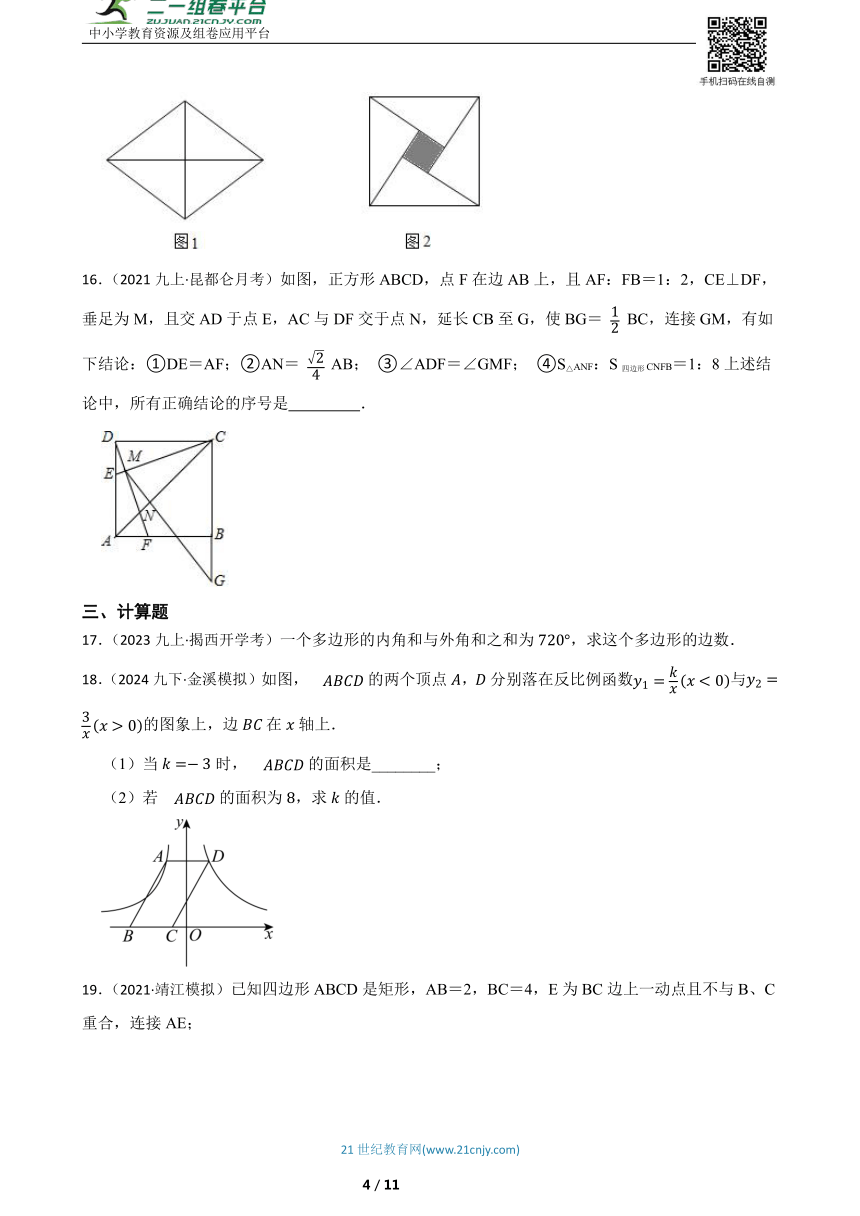
16.(2021九上·昆都仑月考)如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG= BC,连接GM,有如下结论:①DE=AF;②AN= AB; ③∠ADF=∠GMF; ④S△ANF:S四边形CNFB=1:8上述结论中,所有正确结论的序号是 .
三、计算题
17.(2023九上·揭西开学考)一个多边形的内角和与外角和之和为,求这个多边形的边数.
18.(2024九下·金溪模拟)如图,的两个顶点,分别落在反比例函数与的图象上,边在轴上.
(1)当时,的面积是________;
(2)若的面积为,求的值.
19.(2021·靖江模拟)已知四边形ABCD是矩形,AB=2,BC=4,E为BC边上一动点且不与B、C重合,连接AE;
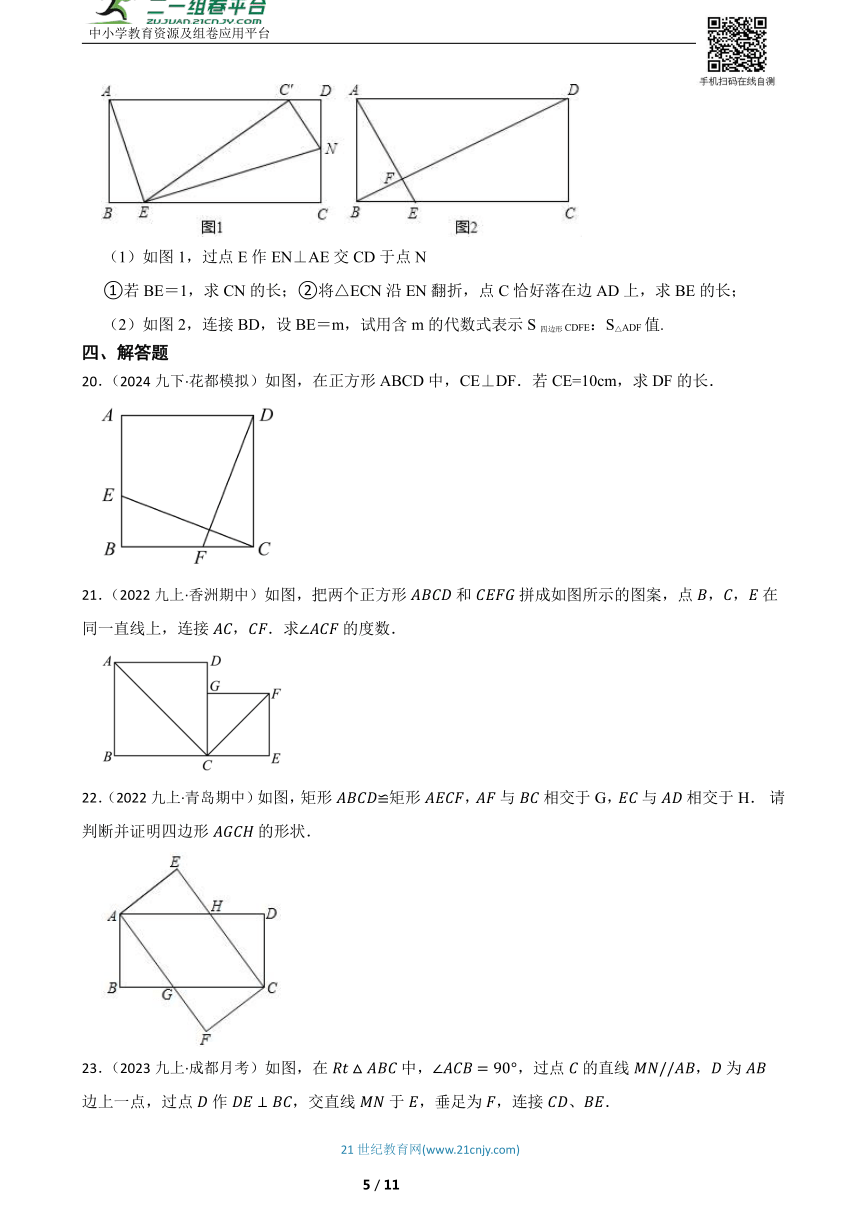
(1)如图1,过点E作EN⊥AE交CD于点N
①若BE=1,求CN的长;②将△ECN沿EN翻折,点C恰好落在边AD上,求BE的长;
(2)如图2,连接BD,设BE=m,试用含m的代数式表示S四边形CDFE:S△ADF值.
四、解答题
20.(2024九下·花都模拟)如图,在正方形ABCD中,CE⊥DF.若CE=10cm,求DF的长.
21.(2022九上·香洲期中)如图,把两个正方形和拼成如图所示的图案,点,,在同一直线上,连接,.求的度数.
22.(2022九上·青岛期中)如图,矩形矩形,与相交于G,与相交于H. 请判断并证明四边形的形状.
23.(2023九上·成都月考)如图,在中,,过点的直线,为边上一点,过点作,交直线于,垂足为,连接、.
(1)求证:;
(2)当在中点时,四边形是什么特殊四边形?说明你的理由;
(3)若为中点,则当的大小满足什么条件时,四边形是正方形?请说明你的理由.
答案解析部分
1.【答案】C
【知识点】菱形的性质
2.【答案】C
【知识点】菱形的性质;正方形的性质
3.【答案】A
【知识点】矩形的性质
4.【答案】C
【知识点】平行四边形的判定;三角形的中位线定理
5.【答案】A
【知识点】平行四边形的性质;三角形的中位线定理
6.【答案】D
【知识点】平行四边形的判定;菱形的判定;矩形的判定;三角形的中位线定理
7.【答案】A
【知识点】菱形的性质;三角形的中位线定理
8.【答案】C
【知识点】平行四边形的判定;三角形的中位线定理
9.【答案】D
【知识点】正方形的性质
10.【答案】D
【知识点】正方形的性质;四边形的综合
11.【答案】
【知识点】三角形的中位线定理
12.【答案】
【知识点】平行四边形的性质
13.【答案】24
【知识点】菱形的性质
14.【答案】菱形
【知识点】菱形的判定;矩形的性质;三角形的中位线定理
15.【答案】4
【知识点】菱形的性质
16.【答案】①②③
【知识点】正方形的性质;四边形的综合
17.【答案】这个多边形的边数为4
【知识点】多边形内角与外角
18.【答案】(1);
(2).
【知识点】平行四边形的性质
19.【答案】(1)解:①∵BE=1,
∴CE=BC﹣BE=4﹣1=3,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECN,
∴ = ,
即: = ,
解得:CN= ;
②过点E作EF⊥AD于F,如图1所示:
则四边形ABEF是矩形,
∴AB=EF=2,AF=BE,
由折叠的性质得:CE=C′E,CN=C′N,∠EC′N=∠C=90°,
∴∠NC′D+∠EC′F=90°,
∵∠C′ND+∠NC′D=90°,
∴∠EC′F=∠C′ND,
∵∠D=∠EFC′,
∴△EC′F∽△NC′D,
∴ = = ,
∴ = = ,
∵ = ,
∴ = ,
∴ = = ,
∴C′D=BE,
设BE=x,则C′D=AF=x,C′F=4﹣2x,CE=4﹣x,
∴ = , = ,
∴DN=x(2﹣x),CN= ,
∴CN+DN=x(2﹣x)+ =CD=2,
解得:x=2或x= ,
∴BE=2或BE= ;
(2)解:∵四边形ABCD为矩形,
∴BC=AD,AD∥BC,
∴△ADF∽△EBF,
∴ = = ,
∴ =( )2= ,
∴S△ADF= s△BEF,
S△ABF= = = S△BEF,
S四边形CDFE=S△ADF+S△ABF﹣S△BEF= S△BEF+ S△BEF﹣S△BEF=( + ﹣1)S△BEF,
∴S四边形CDFE:S△ADF=( + ﹣1)S△BEF: s△BEF=1+ ﹣ .
【知识点】四边形的综合
20.【答案】10cm
【知识点】正方形的性质
21.【答案】
【知识点】正方形的性质
22.【答案】解:四边形为菱形,证明如下:
∵矩形矩形,
∴,
∴,
∴,
在和中,
,
∴,
同理可得,
在和中,
,
∴,
∴,
∴,
∴四边形是菱形.
【知识点】菱形的判定
23.【答案】(1)证明:.
.
,
,
,
,即,
四边形是平行四边形,
(2)解:四边形是菱形.
理由是:为中点,
,
,
.
,
四边形是平行四边形.
,为中点,
,
平行四边形是菱形.
(3)解:当时,四边形是正方形.
理由是:,,
,
.
为中点,
,
,
四边形是菱形,
菱形是正方形,
即当时,四边形是正方形.
【知识点】平行四边形的判定与性质;菱形的判定与性质;正方形的判定
21世纪教育网(www.21cnjy.com)
11 / 11
2025年中考数学九年级
一轮复习【图形的性质】专题(四边形)部分过关题
一、单选题
1.(2023九上·福田期中)已知菱形 的对角线 , 的长度分别为8 和6 ,则菱形 的周长是( )
A.10 B.16 C.20 D.40
2.(2024八下·凉州期中)正方形具有而菱形不具有的性质是( )
A.对角相等 B.对角线互相平分
C.对角线相等 D.四条边都相等
3.(2023·大渡口模拟)矩形中,,,则的长为( )
A.5 B.4 C.3 D.2
4.(2024九下·怀化模拟)如图,△ABC边AB,BC,AC上的中点分别是D,E,F,且各边的长度分别为5厘米,4厘米,6厘米,则四边形ADEF的周长是( )
A.9厘米 B.10厘米 C.11厘米 D.12厘米
5.(2024九下·罗湖模拟)如图,已知平行四边形的面积为,为的中点,连接,则的面积为( )
A. B. C. D.
6.(2024八下·崇义期中)如图,点E,F,G,H分别为四边形ABCD的边AB,BC,CD,DA的中点.下列三种说法:
① .四边形EFGH一定是平行四边形;
②.若AC=BD,则四边形EFGH 是菱形;
③.若AC⊥BD,则四边形EFGH是矩形.
其中正确的是( )
A.① B.①② C.①③ D.①②③
7.(2024九上·柳南月考)如图,在菱形中,、分别是、的中点,如果,那么菱形的周长是( )
A.16 B.8 C.4 D.2
8.如图,沿Rt△ABC的中位线DE剪切一刀后,用得到的△ADE和四边形DBCE拼图,下列图形:①平行四边形;②菱形;③矩形;④等腰梯形.一定能拼出的是( )
A.只有①② B.只有③④ C.只有①③④ D.①②③④
9.(2024·宁海)如图四边形与是并列放在一起的两个正方形,是与的交点.如果正方形的面积是9,,则的面积为
A.1 B. C.4 D.
10.(2021·惠城模拟)如图,正方形 的边 ,对角线 和 交于点 , 是边 上靠近点 的三等分点,连接 , ,分别交 , 于点 , ,连接 .有下列结论:① ;② ;③ ;④ .其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题
11.(2024九上·衡阳期中)如图,在中,平分,于点,延长交于点,是的中点,若,,则 .
12.(2024九下·集美模拟)如图,平行四边形的对角线,相交于点O,,的周长为5,则 .
13.(2019九上·靖远月考)若菱形的两条对角线长分别是6㎝和8㎝,则该菱形的面积是 ㎝2.
14.(2020九上·金台期中)顺次连接矩形各边中点所得四边形为 .
15.(2022八下·连云期中)把图1中边长为10的菱形沿对角线分成四个全等的直角三角形,且此菱形的一条对角线长为16,将这四个直角三角形拼成如图2所示的正方形,则图2中的阴影的面积为 .
16.(2021九上·昆都仑月考)如图,正方形ABCD,点F在边AB上,且AF:FB=1:2,CE⊥DF,垂足为M,且交AD于点E,AC与DF交于点N,延长CB至G,使BG= BC,连接GM,有如下结论:①DE=AF;②AN= AB; ③∠ADF=∠GMF; ④S△ANF:S四边形CNFB=1:8上述结论中,所有正确结论的序号是 .
三、计算题
17.(2023九上·揭西开学考)一个多边形的内角和与外角和之和为,求这个多边形的边数.
18.(2024九下·金溪模拟)如图,的两个顶点,分别落在反比例函数与的图象上,边在轴上.
(1)当时,的面积是________;
(2)若的面积为,求的值.
19.(2021·靖江模拟)已知四边形ABCD是矩形,AB=2,BC=4,E为BC边上一动点且不与B、C重合,连接AE;
(1)如图1,过点E作EN⊥AE交CD于点N
①若BE=1,求CN的长;②将△ECN沿EN翻折,点C恰好落在边AD上,求BE的长;
(2)如图2,连接BD,设BE=m,试用含m的代数式表示S四边形CDFE:S△ADF值.
四、解答题
20.(2024九下·花都模拟)如图,在正方形ABCD中,CE⊥DF.若CE=10cm,求DF的长.
21.(2022九上·香洲期中)如图,把两个正方形和拼成如图所示的图案,点,,在同一直线上,连接,.求的度数.
22.(2022九上·青岛期中)如图,矩形矩形,与相交于G,与相交于H. 请判断并证明四边形的形状.
23.(2023九上·成都月考)如图,在中,,过点的直线,为边上一点,过点作,交直线于,垂足为,连接、.
(1)求证:;
(2)当在中点时,四边形是什么特殊四边形?说明你的理由;
(3)若为中点,则当的大小满足什么条件时,四边形是正方形?请说明你的理由.
答案解析部分
1.【答案】C
【知识点】菱形的性质
2.【答案】C
【知识点】菱形的性质;正方形的性质
3.【答案】A
【知识点】矩形的性质
4.【答案】C
【知识点】平行四边形的判定;三角形的中位线定理
5.【答案】A
【知识点】平行四边形的性质;三角形的中位线定理
6.【答案】D
【知识点】平行四边形的判定;菱形的判定;矩形的判定;三角形的中位线定理
7.【答案】A
【知识点】菱形的性质;三角形的中位线定理
8.【答案】C
【知识点】平行四边形的判定;三角形的中位线定理
9.【答案】D
【知识点】正方形的性质
10.【答案】D
【知识点】正方形的性质;四边形的综合
11.【答案】
【知识点】三角形的中位线定理
12.【答案】
【知识点】平行四边形的性质
13.【答案】24
【知识点】菱形的性质
14.【答案】菱形
【知识点】菱形的判定;矩形的性质;三角形的中位线定理
15.【答案】4
【知识点】菱形的性质
16.【答案】①②③
【知识点】正方形的性质;四边形的综合
17.【答案】这个多边形的边数为4
【知识点】多边形内角与外角
18.【答案】(1);
(2).
【知识点】平行四边形的性质
19.【答案】(1)解:①∵BE=1,
∴CE=BC﹣BE=4﹣1=3,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∴∠BAE+∠BEA=90°,
∵EF⊥AE,
∴∠AEF=90°,
∴∠BEA+∠FEC=90°,
∴∠BAE=∠FEC,
∴△ABE∽△ECN,
∴ = ,
即: = ,
解得:CN= ;
②过点E作EF⊥AD于F,如图1所示:
则四边形ABEF是矩形,
∴AB=EF=2,AF=BE,
由折叠的性质得:CE=C′E,CN=C′N,∠EC′N=∠C=90°,
∴∠NC′D+∠EC′F=90°,
∵∠C′ND+∠NC′D=90°,
∴∠EC′F=∠C′ND,
∵∠D=∠EFC′,
∴△EC′F∽△NC′D,
∴ = = ,
∴ = = ,
∵ = ,
∴ = ,
∴ = = ,
∴C′D=BE,
设BE=x,则C′D=AF=x,C′F=4﹣2x,CE=4﹣x,
∴ = , = ,
∴DN=x(2﹣x),CN= ,
∴CN+DN=x(2﹣x)+ =CD=2,
解得:x=2或x= ,
∴BE=2或BE= ;
(2)解:∵四边形ABCD为矩形,
∴BC=AD,AD∥BC,
∴△ADF∽△EBF,
∴ = = ,
∴ =( )2= ,
∴S△ADF= s△BEF,
S△ABF= = = S△BEF,
S四边形CDFE=S△ADF+S△ABF﹣S△BEF= S△BEF+ S△BEF﹣S△BEF=( + ﹣1)S△BEF,
∴S四边形CDFE:S△ADF=( + ﹣1)S△BEF: s△BEF=1+ ﹣ .
【知识点】四边形的综合
20.【答案】10cm
【知识点】正方形的性质
21.【答案】
【知识点】正方形的性质
22.【答案】解:四边形为菱形,证明如下:
∵矩形矩形,
∴,
∴,
∴,
在和中,
,
∴,
同理可得,
在和中,
,
∴,
∴,
∴,
∴四边形是菱形.
【知识点】菱形的判定
23.【答案】(1)证明:.
.
,
,
,
,即,
四边形是平行四边形,
(2)解:四边形是菱形.
理由是:为中点,
,
,
.
,
四边形是平行四边形.
,为中点,
,
平行四边形是菱形.
(3)解:当时,四边形是正方形.
理由是:,,
,
.
为中点,
,
,
四边形是菱形,
菱形是正方形,
即当时,四边形是正方形.
【知识点】平行四边形的判定与性质;菱形的判定与性质;正方形的判定
21世纪教育网(www.21cnjy.com)
11 / 11
同课章节目录
