2025年中考数学九年级一轮复习【图形的变化】专题(图形的相似部分)过关题
文档属性
| 名称 | 2025年中考数学九年级一轮复习【图形的变化】专题(图形的相似部分)过关题 |  | |
| 格式 | docx | ||
| 文件大小 | 429.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 14:42:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年中考数学九年级
一轮复习【图形的变化】专题(图形的相似)部分过关题
一、单选题
1.(2024九上·遂宁期中)下面四组线段中,成比例的是( )
A. B.
C. D.a=
2.(2019九上·太原期中)如图,直线a∥b∥c,点A,B在直线a上,点C,D在直线c上,线段AC,BD分别交直线b于点E,F,则下列线段的比与 一定相等的是( )
A. B. C. D.
3.(2023九上·蚌埠期中)下列两个图形不一定是相似图形的是( )
A.两个圆 B.两个正方形
C.两个等边三角形 D.两个等腰三角形
4.(2023九上·射洪期中)如图,已知.若,,则等于( )
A.3 B.4 C.5 D.6
5.(2024九下·兰州模拟)如图,在中,,若,则( )
A. B. C. D.
6.(2019九上·象山期末)如图,矩形ABCD∽矩形DEFC,且面积比为4:1,则AE:ED的值为( )
A.4:1 B.3:1 C.2:1 D.3:2
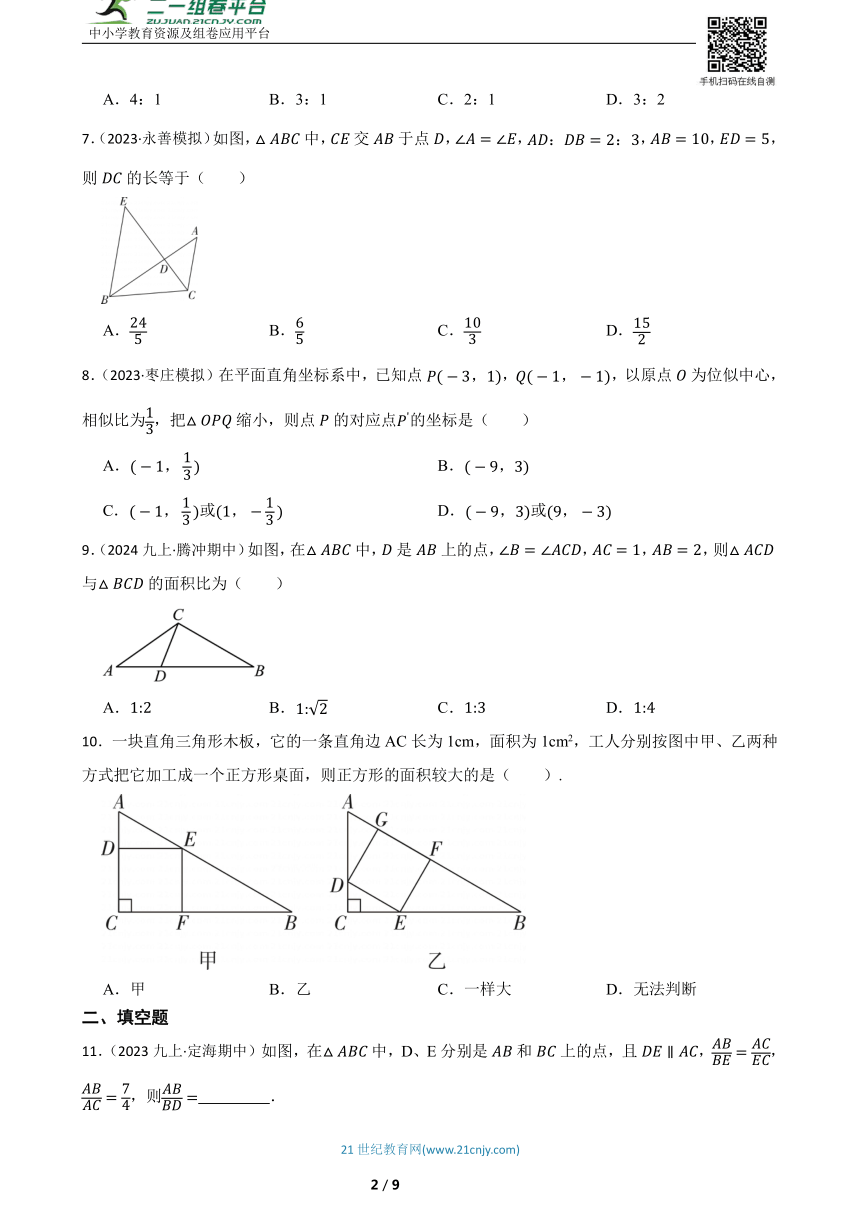
7.(2023·永善模拟)如图,中,交于点,,,,,则的长等于( )
A. B. C. D.
8.(2023·枣庄模拟)在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是( )
A. B.
C.或 D.或
9.(2024九上·腾冲期中)如图,在中,是上的点,,,,则与的面积比为( )
A. B. C. D.
10.一块直角三角形木板,它的一条直角边AC长为1cm,面积为1cm2,工人分别按图中甲、乙两种方式把它加工成一个正方形桌面,则正方形的面积较大的是( ).
A.甲 B.乙 C.一样大 D.无法判断
二、填空题
11.(2023九上·定海期中)如图,在中,D、E分别是和上的点,且,, ,则 .
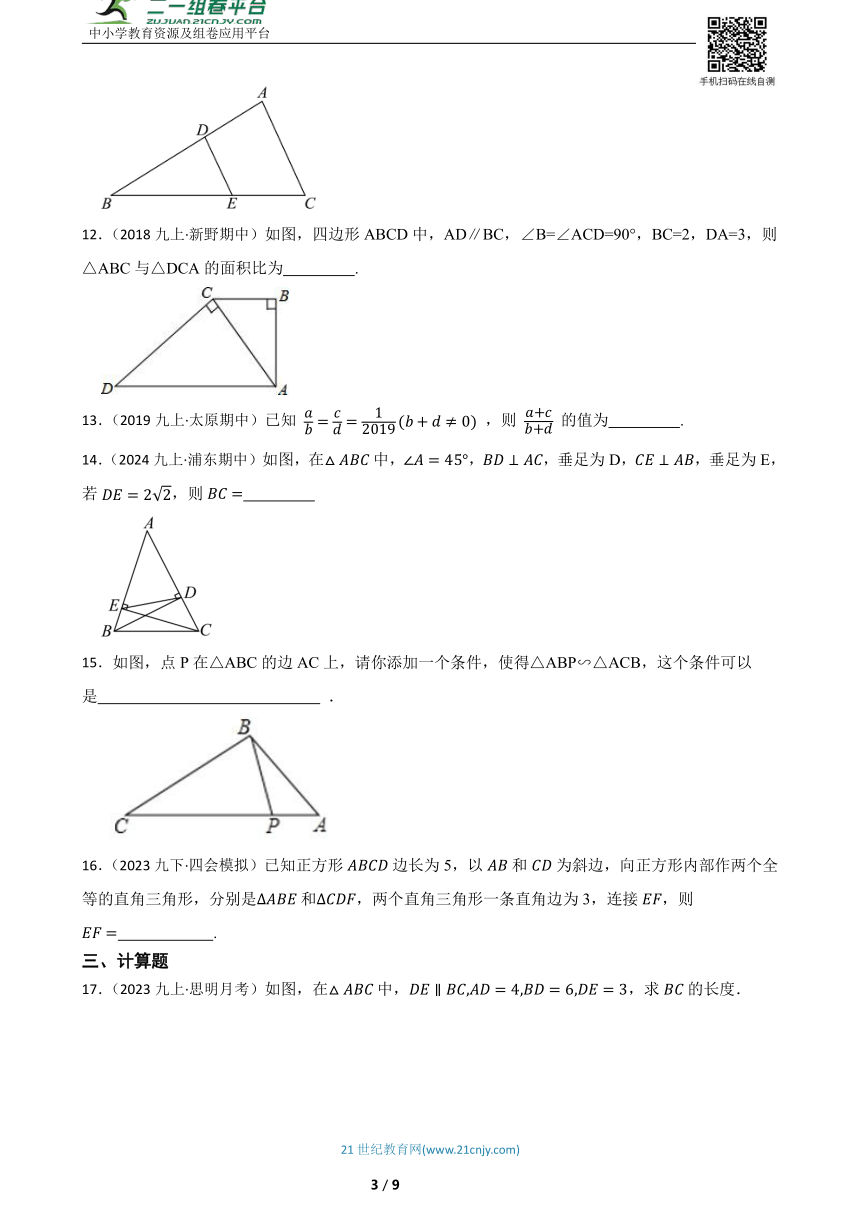
12.(2018九上·新野期中)如图,四边形ABCD中,AD∥BC,∠B=∠ACD=90°,BC=2,DA=3,则△ABC与△DCA的面积比为 .
13.(2019九上·太原期中)已知 ,则 的值为 .
14.(2024九上·浦东期中)如图,在中,,,垂足为D,,垂足为E,若,则
15.如图,点P在△ABC的边AC上,请你添加一个条件,使得△ABP∽△ACB,这个条件可以是 .
16.(2023九下·四会模拟)已知正方形边长为5,以和为斜边,向正方形内部作两个全等的直角三角形,分别是和,两个直角三角形一条直角边为3,连接,则 .
三、计算题
17.(2023九上·思明月考)如图,在中,,求的长度.
18.已知,求代数式的值.
19.(2023九上·江汉月考)抛物线交轴于A,B两点(点A在点B的左边),交y轴正半轴于点C.
(1)如图1,当时,
①直接写出点的坐标;
②若抛物线上有一点P,使,求点P的坐标.
(2)如图2,平移直线交抛物线于M,N两点,直线与直线交于点G,若点G在定直线上运动,求m的值.
四、解答题
20.(2023九上·宁海月考)已知线段a、b、c满足,且.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x的值.
21.(2024九上·奉贤期中)如图,已知直线l1、l2、l3分别截直线l4于点A、B、C,截直线l5于点D、E、F,且
(1)如果AB=3,BC=6,DE=4,求EF的长;
(2)如果DE:EF=2:3,AC=25,求AB的长.
22.(2023九上·礼泉期末)小丽想利用所学知识测量旗杆AB的高度,如图,小丽在自家窗边看见旗杆和住宅楼之间有一棵大树DE,小丽通过调整自己的位置,发现半蹲于窗边,眼睛位于C处时,恰好看到旗杆顶端A、大树顶端D在一条直线上,测得EF=4米,BE=12米,眼睛到地面的距离CF为3.5米,已知大树DE的高度为7米,CG⊥AB于点G,AB⊥BF于点B,DE⊥BF于点E,交CG于点H,CF⊥BF于点F.请你根据以上信息帮小丽求出旗杆AB的高度.
23.(2022九上·北海月考)如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=4,∠BAC=45°.
(1)直接写出点A的坐标________点 C的坐标________;
(2)若反比例函数y=的图象经过点B,求k的值;
(3)如图过点B作BD⊥y轴于点D;在y轴上是否存在点P,使以P,B,D为顶点的三角形与以P, O,A为顶点的三角形相似 若存在,直接写出满足条件的点P的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】比例线段
2.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
3.【答案】D
【知识点】图形的相似
4.【答案】D
【知识点】相似三角形的判定与性质
5.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
6.【答案】B
【知识点】相似多边形
7.【答案】A
【知识点】相似三角形的判定与性质
8.【答案】C
【知识点】位似变换
9.【答案】C
【知识点】相似三角形的判定与性质
10.【答案】A
【知识点】相似三角形的应用
11.【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
12.【答案】4∶9
【知识点】相似三角形的判定与性质
13.【答案】
【知识点】比例的性质
14.【答案】4
【知识点】相似三角形的判定与性质
15.【答案】∠ABP=∠C(答案不唯一)
【知识点】相似三角形的判定
16.【答案】或
【知识点】相似三角形的应用
17.【答案】
【知识点】相似三角形的判定与性质
18.【答案】解:∵,∴可设,则a=2k , b=3k,∴===
【知识点】比例的性质
19.【答案】(1)①,,②
(2)
【知识点】相似三角形的判定与性质
20.【答案】(1)
(2)
【知识点】比例的性质;比例线段
21.【答案】(1);(2)
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
22.【答案】解:由题意知BG=HE=CF=3.5米,CH=EF=4米,GH=BE=12米,
∴DH=DE-HE=7-3.5=3.5(米),CG=GH+CH=12+4=16(米),
∵AB⊥BF,DE⊥BF,∴AB∥DE,
∵ CG⊥AB,∴CG⊥DE,
∴∠DHC=∠AGC=90°,
∵ ∠DCH=∠ACG,
∴△DHC∽△AGC,
即
∴AG=14(米),
∴AB=AG+GB=14+3.5=17.5(米),
答:旗杆AB的高度为17.5米.
【知识点】相似三角形的应用
23.【答案】(1)(-6,0),(6,0);(2)k=16;(3)点P的坐标为:(0,2)或(0,6)或(0,12)或(0,4+2)或(0,4-2).
【知识点】相似三角形的判定与性质
21世纪教育网(www.21cnjy.com)
2 / 9
2025年中考数学九年级
一轮复习【图形的变化】专题(图形的相似)部分过关题
一、单选题
1.(2024九上·遂宁期中)下面四组线段中,成比例的是( )
A. B.
C. D.a=
2.(2019九上·太原期中)如图,直线a∥b∥c,点A,B在直线a上,点C,D在直线c上,线段AC,BD分别交直线b于点E,F,则下列线段的比与 一定相等的是( )
A. B. C. D.
3.(2023九上·蚌埠期中)下列两个图形不一定是相似图形的是( )
A.两个圆 B.两个正方形
C.两个等边三角形 D.两个等腰三角形
4.(2023九上·射洪期中)如图,已知.若,,则等于( )
A.3 B.4 C.5 D.6
5.(2024九下·兰州模拟)如图,在中,,若,则( )
A. B. C. D.
6.(2019九上·象山期末)如图,矩形ABCD∽矩形DEFC,且面积比为4:1,则AE:ED的值为( )
A.4:1 B.3:1 C.2:1 D.3:2
7.(2023·永善模拟)如图,中,交于点,,,,,则的长等于( )
A. B. C. D.
8.(2023·枣庄模拟)在平面直角坐标系中,已知点,,以原点为位似中心,相似比为,把缩小,则点的对应点的坐标是( )
A. B.
C.或 D.或
9.(2024九上·腾冲期中)如图,在中,是上的点,,,,则与的面积比为( )
A. B. C. D.
10.一块直角三角形木板,它的一条直角边AC长为1cm,面积为1cm2,工人分别按图中甲、乙两种方式把它加工成一个正方形桌面,则正方形的面积较大的是( ).
A.甲 B.乙 C.一样大 D.无法判断
二、填空题
11.(2023九上·定海期中)如图,在中,D、E分别是和上的点,且,, ,则 .
12.(2018九上·新野期中)如图,四边形ABCD中,AD∥BC,∠B=∠ACD=90°,BC=2,DA=3,则△ABC与△DCA的面积比为 .
13.(2019九上·太原期中)已知 ,则 的值为 .
14.(2024九上·浦东期中)如图,在中,,,垂足为D,,垂足为E,若,则
15.如图,点P在△ABC的边AC上,请你添加一个条件,使得△ABP∽△ACB,这个条件可以是 .
16.(2023九下·四会模拟)已知正方形边长为5,以和为斜边,向正方形内部作两个全等的直角三角形,分别是和,两个直角三角形一条直角边为3,连接,则 .
三、计算题
17.(2023九上·思明月考)如图,在中,,求的长度.
18.已知,求代数式的值.
19.(2023九上·江汉月考)抛物线交轴于A,B两点(点A在点B的左边),交y轴正半轴于点C.
(1)如图1,当时,
①直接写出点的坐标;
②若抛物线上有一点P,使,求点P的坐标.
(2)如图2,平移直线交抛物线于M,N两点,直线与直线交于点G,若点G在定直线上运动,求m的值.
四、解答题
20.(2023九上·宁海月考)已知线段a、b、c满足,且.
(1)求a、b、c的值;
(2)若线段x是线段a、b的比例中项,求x的值.
21.(2024九上·奉贤期中)如图,已知直线l1、l2、l3分别截直线l4于点A、B、C,截直线l5于点D、E、F,且
(1)如果AB=3,BC=6,DE=4,求EF的长;
(2)如果DE:EF=2:3,AC=25,求AB的长.
22.(2023九上·礼泉期末)小丽想利用所学知识测量旗杆AB的高度,如图,小丽在自家窗边看见旗杆和住宅楼之间有一棵大树DE,小丽通过调整自己的位置,发现半蹲于窗边,眼睛位于C处时,恰好看到旗杆顶端A、大树顶端D在一条直线上,测得EF=4米,BE=12米,眼睛到地面的距离CF为3.5米,已知大树DE的高度为7米,CG⊥AB于点G,AB⊥BF于点B,DE⊥BF于点E,交CG于点H,CF⊥BF于点F.请你根据以上信息帮小丽求出旗杆AB的高度.
23.(2022九上·北海月考)如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=4,∠BAC=45°.
(1)直接写出点A的坐标________点 C的坐标________;
(2)若反比例函数y=的图象经过点B,求k的值;
(3)如图过点B作BD⊥y轴于点D;在y轴上是否存在点P,使以P,B,D为顶点的三角形与以P, O,A为顶点的三角形相似 若存在,直接写出满足条件的点P的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】A
【知识点】比例线段
2.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
3.【答案】D
【知识点】图形的相似
4.【答案】D
【知识点】相似三角形的判定与性质
5.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
6.【答案】B
【知识点】相似多边形
7.【答案】A
【知识点】相似三角形的判定与性质
8.【答案】C
【知识点】位似变换
9.【答案】C
【知识点】相似三角形的判定与性质
10.【答案】A
【知识点】相似三角形的应用
11.【答案】
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
12.【答案】4∶9
【知识点】相似三角形的判定与性质
13.【答案】
【知识点】比例的性质
14.【答案】4
【知识点】相似三角形的判定与性质
15.【答案】∠ABP=∠C(答案不唯一)
【知识点】相似三角形的判定
16.【答案】或
【知识点】相似三角形的应用
17.【答案】
【知识点】相似三角形的判定与性质
18.【答案】解:∵,∴可设,则a=2k , b=3k,∴===
【知识点】比例的性质
19.【答案】(1)①,,②
(2)
【知识点】相似三角形的判定与性质
20.【答案】(1)
(2)
【知识点】比例的性质;比例线段
21.【答案】(1);(2)
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
22.【答案】解:由题意知BG=HE=CF=3.5米,CH=EF=4米,GH=BE=12米,
∴DH=DE-HE=7-3.5=3.5(米),CG=GH+CH=12+4=16(米),
∵AB⊥BF,DE⊥BF,∴AB∥DE,
∵ CG⊥AB,∴CG⊥DE,
∴∠DHC=∠AGC=90°,
∵ ∠DCH=∠ACG,
∴△DHC∽△AGC,
即
∴AG=14(米),
∴AB=AG+GB=14+3.5=17.5(米),
答:旗杆AB的高度为17.5米.
【知识点】相似三角形的应用
23.【答案】(1)(-6,0),(6,0);(2)k=16;(3)点P的坐标为:(0,2)或(0,6)或(0,12)或(0,4+2)或(0,4-2).
【知识点】相似三角形的判定与性质
21世纪教育网(www.21cnjy.com)
2 / 9
同课章节目录
