2025年中考数学九年级一轮复习【图形的变动】专题(锐角三角形部分)过关题(含答案)
文档属性
| 名称 | 2025年中考数学九年级一轮复习【图形的变动】专题(锐角三角形部分)过关题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1004.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 14:46:16 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年中考数学九年级
一轮复习【图形的变动】专题(锐角三角形)部分过关题
一、单选题
1.(2023·杭州模拟)如图,在中,,D是上一点,连结,若,则的长可表示为( )
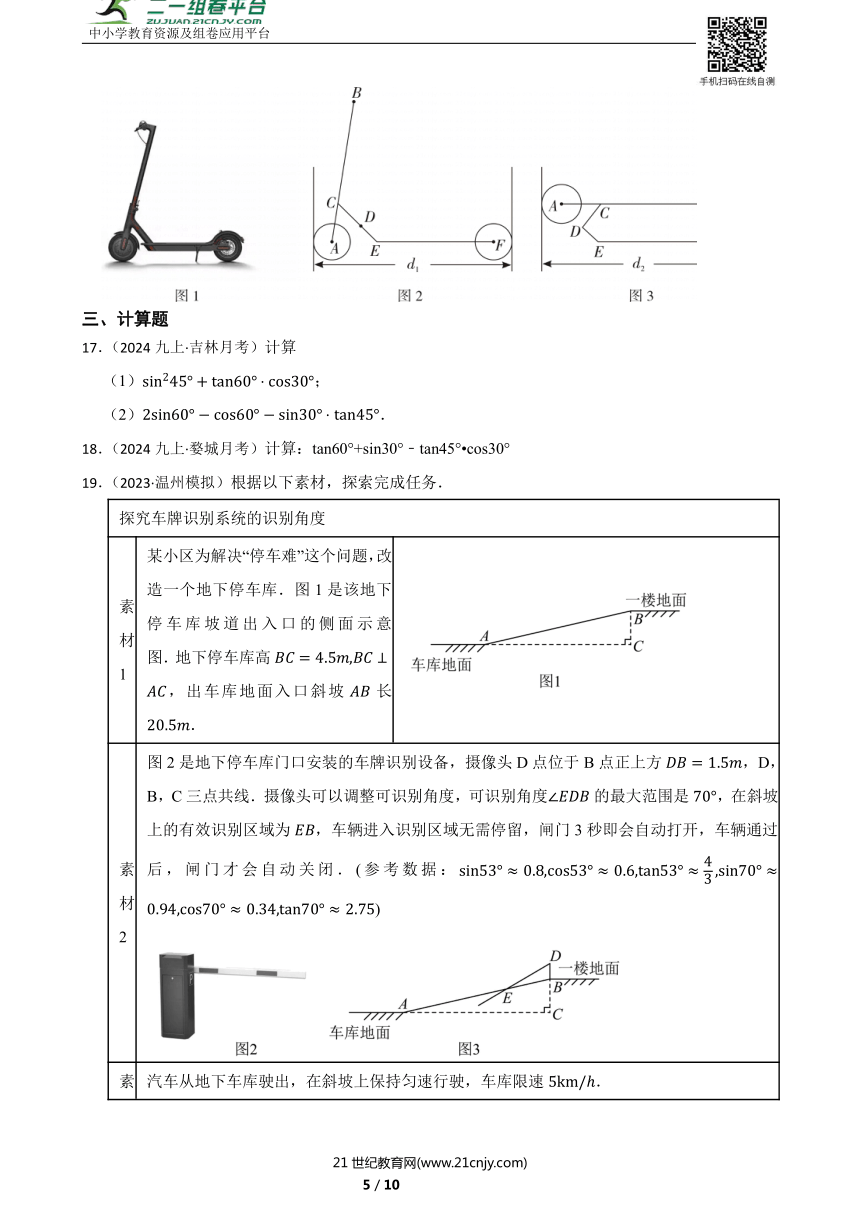
A. B. C. D.
2.(2023九上·淮安月考)若,则锐角的度数为( )
A. B. C. D.
3.(2023九下·三水开学考)下列三角函数中,值为的是( )
A. B. C. D.
4.(2022九下·南宁模拟)如图,在中,,则长为( )
A.4 B.8 C. D.12
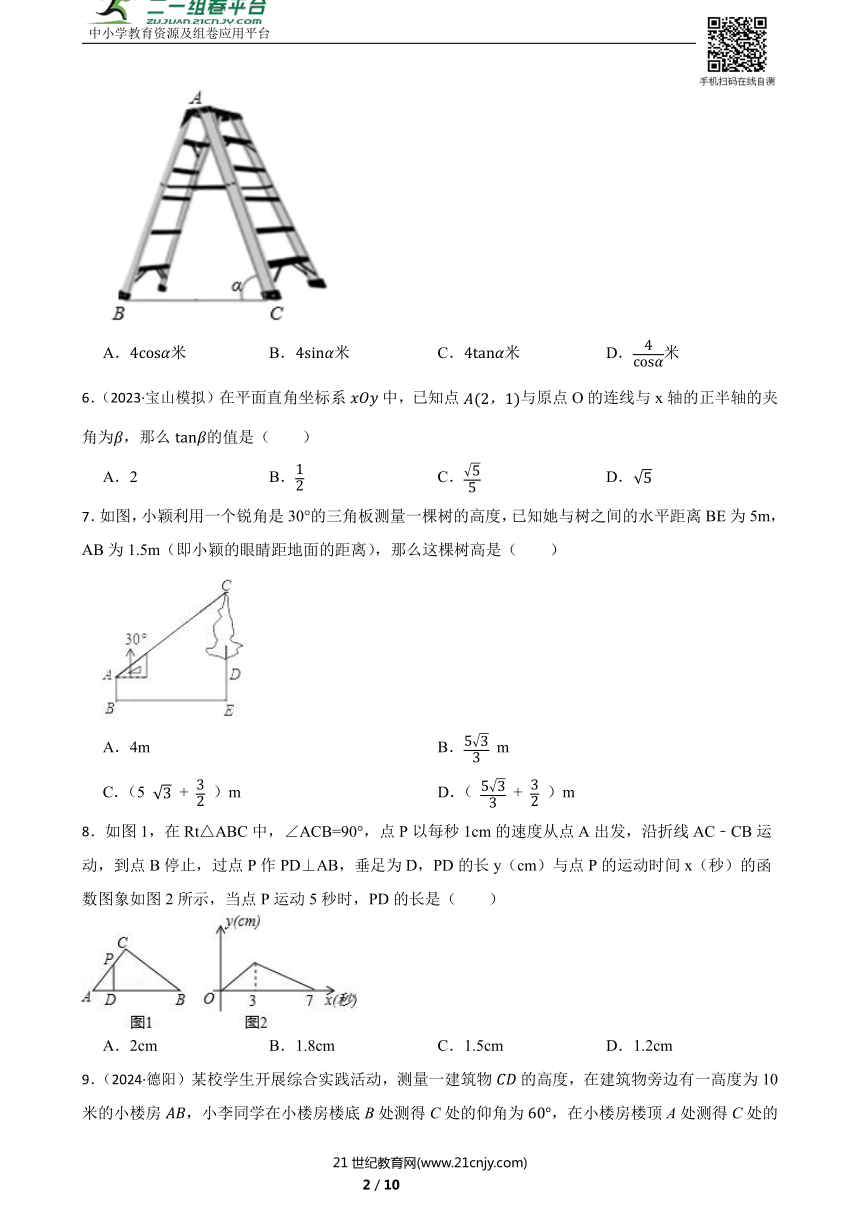
5.(2024九上·兰溪期中)如图是一架人字梯,已知米,AC与地面BC的夹角为,则两梯脚之间的距离BC为( )
A.米 B.米 C.米 D.米
6.(2023·宝山模拟)在平面直角坐标系中,已知点与原点O的连线与x轴的正半轴的夹角为,那么的值是( )
A.2 B. C. D.
7.如图,小颖利用一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )
A.4m B. m
C.(5 + )m D.( + )m
8.如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC﹣CB运动,到点B停止,过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示,当点P运动5秒时,PD的长是( )
A.2cm B.1.8cm C.1.5cm D.1.2cm
9.(2024·德阳)某校学生开展综合实践活动,测量一建筑物的高度,在建筑物旁边有一高度为10米的小楼房,小李同学在小楼房楼底B处测得C处的仰角为,在小楼房楼顶A处测得C处的仰角为.(、在同一平面内,B、D在同一水平面上),则建筑物的高为( )米
A.20 B.15 C.12 D.
10.(2022·宁海)若过点作四条直线构成一个正方形,则该正方形的面积不可能为( )
A. B. C. D.
二、填空题
11.(2024九下·克什克腾旗模拟)如图,甲、乙两人在道路的两边相向而行,当甲、乙两人分别行至点A、C时,测得乙在甲的北偏东方向上.乙留在原地休息,甲继续向前走了40米到B处,此时测得乙在其北偏东方向上.求道路的宽 .
12.(2024九上·金堂月考)如图所示,某人在D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度i=1∶0.5,则山的高度为 米.
13.(2024九下·郑州模拟)如图,一座金字塔被发现时,顶部已经损坏,但底部未曾受损.已知该金字塔的底面是一个边长为的正方形,且每个侧面与底面所夹的角都为,则这座金字塔原来的高为 (用含的式子表示).
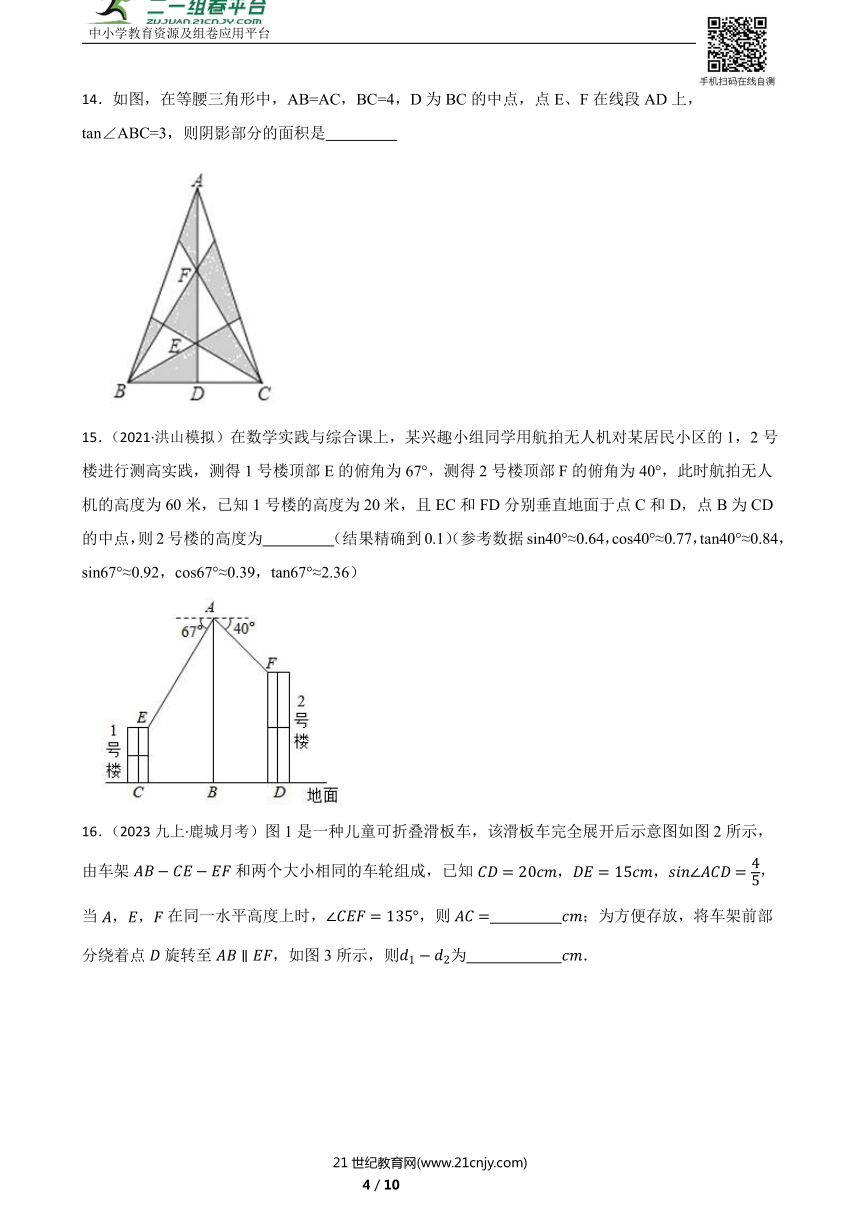
14.如图,在等腰三角形中,AB=AC,BC=4,D为BC的中点,点E、F在线段AD上,tan∠ABC=3,则阴影部分的面积是
15.(2021·洪山模拟)在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1,2号楼进行测高实践,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D,点B为CD的中点,则2号楼的高度为 (结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
16.(2023九上·鹿城月考)图1是一种儿童可折叠滑板车,该滑板车完全展开后示意图如图2所示,由车架和两个大小相同的车轮组成,已知,当在同一水平高度上时,,则 ;为方便存放,将车架前部分绕着点旋转至,如图3所示,则为 .
三、计算题
17.(2024九上·吉林月考)计算
(1);
(2).
18.(2024九上·婺城月考)计算:tan60°+sin30°﹣tan45° cos30°
19.(2023·温州模拟)根据以下素材,探索完成任务.
探究车牌识别系统的识别角度
素材1 某小区为解决“停车难”这个问题,改造一个地下停车库.图1是该地下停车库坡道出入口的侧面示意图.地下停车库高,出车库地面入口斜坡长.
素材2 图2是地下停车库门口安装的车牌识别设备,摄像头D点位于B点正上方,D,B,C三点共线.摄像头可以调整可识别角度,可识别角度的最大范围是,在斜坡上的有效识别区域为,车辆进入识别区域无需停留,闸门3秒即会自动打开,车辆通过后,闸门才会自动关闭.(参考数据:)
素材3 汽车从地下车库驶出,在斜坡上保持匀速行驶,车库限速.
问题解决 任务一 确定斜坡坡比;如图1,求的值.
任务二 判断车辆是否顺利通过:如图3,当时,请判断此时车辆以最高限速行驶到达B点时,闸门是否已经打开,请通过计算说明.
项目反思 任务三 能否通过调整摄像头的识别角度,使汽车以最高限速行驶时,可以顺利通过闸口,请计算的取值范围.
四、解答题
20.(2023九下·枣阳模拟)如图,一架长的梯子斜靠在一竖直的墙面上,梯子与水平地面所成.现将梯子底端向墙面靠近移动到点处,顶端移动到墙面的点处,使梯子与地面所成,求梯子底端向墙面移动了多少米?(结果精确到;参考数据:)
21.(2023九下·巴东模拟)数学学习实践活动小组计划运用所学知识测量学校小山上古塔的高.他们选取适当的位置进行测量,在山下的点A处测得小山上的古塔底部点E的仰角为,向右前进到达点B处,测得古塔顶点的仰角为.已知小山高,A、B、C、E、F五点在同一个平面上.请你根据以上条件求小山上古塔的高(结果保留整数).
参考数据:,,;,,;
22.(2020·昆明模拟)如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到0.1米).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
23.(2020九上·西安月考)在棚户区改造时,要拆除废旧烟囱 (如图),在烟囱正西方向的楼房 的顶端C处,测得烟囱的顶端A的仰角为 ,底端B的俯角为 已量得 .拆除时若让烟囱向正东方向倒下,试问:距离烟囱正东方向 远的一棵大树是否会被歪倒的烟囱砸到?请说明理由.(参考数据: )
答案解析部分
1.【答案】C
【知识点】解直角三角形
2.【答案】A
【知识点】求特殊角的三角函数值
3.【答案】D
【知识点】求特殊角的三角函数值
4.【答案】B
【知识点】已知余弦值求边长
5.【答案】A
【知识点】解直角三角形的其他实际应用
6.【答案】B
【知识点】锐角三角函数的定义
7.【答案】D
【知识点】解直角三角形的其他实际应用
8.【答案】D
【知识点】解直角三角形的其他实际应用
9.【答案】B
【知识点】解直角三角形的实际应用﹣仰角俯角问题
10.【答案】C
【知识点】解直角三角形—边角关系;解直角三角形—面积关系
11.【答案】
【知识点】解直角三角形的实际应用﹣方向角问题
12.【答案】
【知识点】解直角三角形的实际应用﹣坡度坡角问题
13.【答案】
【知识点】解直角三角形的其他实际应用
14.【答案】6
【知识点】解直角三角形
15.【答案】45.8米
【知识点】解直角三角形的实际应用﹣仰角俯角问题
16.【答案】25;
【知识点】解直角三角形—构造直角三角形
17.【答案】(1);
(2).
【知识点】特殊角的三角函数的混合运算
18.【答案】解:原式
.
【知识点】特殊角的三角函数的混合运算
19.【答案】任务一:;任务二:闸门没有打开;任务三:
【知识点】解直角三角形
20.【答案】米
【知识点】解直角三角形的其他实际应用
21.【答案】小山上古塔的高约为.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
22.【答案】解:延长CB交PQ于点D.
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵自动扶梯AB的坡度为1:2.4,
∴==.
设BD=5k米,AD=12k米,则AB=13k米.
∵AB=13米,
∴k=1,
∴BD=5米,AD=12米.
在Rt△CDA中,∠CDA=90゜,∠CAD=42°,
∴CD=AD tan∠CAD≈12×0.90≈10.8米,
∴BC≈5.8米.
答:二楼的层高BC约为5.8米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
23.【答案】解:距离烟囱东方35m远的一棵大树被歪倒的烟囱砸着. 理由如下:
∵ m,∠GCB=30°,∠ACG=45°,
∴ m,
∴
m,
∴ m,
∵ >35,
∴距离烟囱东方35m远的一棵大树被歪倒的烟囱砸着.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21世纪教育网(www.21cnjy.com)
1 / 10
2025年中考数学九年级
一轮复习【图形的变动】专题(锐角三角形)部分过关题
一、单选题
1.(2023·杭州模拟)如图,在中,,D是上一点,连结,若,则的长可表示为( )
A. B. C. D.
2.(2023九上·淮安月考)若,则锐角的度数为( )
A. B. C. D.
3.(2023九下·三水开学考)下列三角函数中,值为的是( )
A. B. C. D.
4.(2022九下·南宁模拟)如图,在中,,则长为( )
A.4 B.8 C. D.12
5.(2024九上·兰溪期中)如图是一架人字梯,已知米,AC与地面BC的夹角为,则两梯脚之间的距离BC为( )
A.米 B.米 C.米 D.米
6.(2023·宝山模拟)在平面直角坐标系中,已知点与原点O的连线与x轴的正半轴的夹角为,那么的值是( )
A.2 B. C. D.
7.如图,小颖利用一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )
A.4m B. m
C.(5 + )m D.( + )m
8.如图1,在Rt△ABC中,∠ACB=90°,点P以每秒1cm的速度从点A出发,沿折线AC﹣CB运动,到点B停止,过点P作PD⊥AB,垂足为D,PD的长y(cm)与点P的运动时间x(秒)的函数图象如图2所示,当点P运动5秒时,PD的长是( )
A.2cm B.1.8cm C.1.5cm D.1.2cm
9.(2024·德阳)某校学生开展综合实践活动,测量一建筑物的高度,在建筑物旁边有一高度为10米的小楼房,小李同学在小楼房楼底B处测得C处的仰角为,在小楼房楼顶A处测得C处的仰角为.(、在同一平面内,B、D在同一水平面上),则建筑物的高为( )米
A.20 B.15 C.12 D.
10.(2022·宁海)若过点作四条直线构成一个正方形,则该正方形的面积不可能为( )
A. B. C. D.
二、填空题
11.(2024九下·克什克腾旗模拟)如图,甲、乙两人在道路的两边相向而行,当甲、乙两人分别行至点A、C时,测得乙在甲的北偏东方向上.乙留在原地休息,甲继续向前走了40米到B处,此时测得乙在其北偏东方向上.求道路的宽 .
12.(2024九上·金堂月考)如图所示,某人在D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度i=1∶0.5,则山的高度为 米.
13.(2024九下·郑州模拟)如图,一座金字塔被发现时,顶部已经损坏,但底部未曾受损.已知该金字塔的底面是一个边长为的正方形,且每个侧面与底面所夹的角都为,则这座金字塔原来的高为 (用含的式子表示).
14.如图,在等腰三角形中,AB=AC,BC=4,D为BC的中点,点E、F在线段AD上,tan∠ABC=3,则阴影部分的面积是
15.(2021·洪山模拟)在数学实践与综合课上,某兴趣小组同学用航拍无人机对某居民小区的1,2号楼进行测高实践,测得1号楼顶部E的俯角为67°,测得2号楼顶部F的俯角为40°,此时航拍无人机的高度为60米,已知1号楼的高度为20米,且EC和FD分别垂直地面于点C和D,点B为CD的中点,则2号楼的高度为 (结果精确到0.1)(参考数据sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin67°≈0.92,cos67°≈0.39,tan67°≈2.36)
16.(2023九上·鹿城月考)图1是一种儿童可折叠滑板车,该滑板车完全展开后示意图如图2所示,由车架和两个大小相同的车轮组成,已知,当在同一水平高度上时,,则 ;为方便存放,将车架前部分绕着点旋转至,如图3所示,则为 .
三、计算题
17.(2024九上·吉林月考)计算
(1);
(2).
18.(2024九上·婺城月考)计算:tan60°+sin30°﹣tan45° cos30°
19.(2023·温州模拟)根据以下素材,探索完成任务.
探究车牌识别系统的识别角度
素材1 某小区为解决“停车难”这个问题,改造一个地下停车库.图1是该地下停车库坡道出入口的侧面示意图.地下停车库高,出车库地面入口斜坡长.
素材2 图2是地下停车库门口安装的车牌识别设备,摄像头D点位于B点正上方,D,B,C三点共线.摄像头可以调整可识别角度,可识别角度的最大范围是,在斜坡上的有效识别区域为,车辆进入识别区域无需停留,闸门3秒即会自动打开,车辆通过后,闸门才会自动关闭.(参考数据:)
素材3 汽车从地下车库驶出,在斜坡上保持匀速行驶,车库限速.
问题解决 任务一 确定斜坡坡比;如图1,求的值.
任务二 判断车辆是否顺利通过:如图3,当时,请判断此时车辆以最高限速行驶到达B点时,闸门是否已经打开,请通过计算说明.
项目反思 任务三 能否通过调整摄像头的识别角度,使汽车以最高限速行驶时,可以顺利通过闸口,请计算的取值范围.
四、解答题
20.(2023九下·枣阳模拟)如图,一架长的梯子斜靠在一竖直的墙面上,梯子与水平地面所成.现将梯子底端向墙面靠近移动到点处,顶端移动到墙面的点处,使梯子与地面所成,求梯子底端向墙面移动了多少米?(结果精确到;参考数据:)
21.(2023九下·巴东模拟)数学学习实践活动小组计划运用所学知识测量学校小山上古塔的高.他们选取适当的位置进行测量,在山下的点A处测得小山上的古塔底部点E的仰角为,向右前进到达点B处,测得古塔顶点的仰角为.已知小山高,A、B、C、E、F五点在同一个平面上.请你根据以上条件求小山上古塔的高(结果保留整数).
参考数据:,,;,,;
22.(2020·昆明模拟)如图1,某超市从底楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,求二楼的层高BC(精确到0.1米).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
23.(2020九上·西安月考)在棚户区改造时,要拆除废旧烟囱 (如图),在烟囱正西方向的楼房 的顶端C处,测得烟囱的顶端A的仰角为 ,底端B的俯角为 已量得 .拆除时若让烟囱向正东方向倒下,试问:距离烟囱正东方向 远的一棵大树是否会被歪倒的烟囱砸到?请说明理由.(参考数据: )
答案解析部分
1.【答案】C
【知识点】解直角三角形
2.【答案】A
【知识点】求特殊角的三角函数值
3.【答案】D
【知识点】求特殊角的三角函数值
4.【答案】B
【知识点】已知余弦值求边长
5.【答案】A
【知识点】解直角三角形的其他实际应用
6.【答案】B
【知识点】锐角三角函数的定义
7.【答案】D
【知识点】解直角三角形的其他实际应用
8.【答案】D
【知识点】解直角三角形的其他实际应用
9.【答案】B
【知识点】解直角三角形的实际应用﹣仰角俯角问题
10.【答案】C
【知识点】解直角三角形—边角关系;解直角三角形—面积关系
11.【答案】
【知识点】解直角三角形的实际应用﹣方向角问题
12.【答案】
【知识点】解直角三角形的实际应用﹣坡度坡角问题
13.【答案】
【知识点】解直角三角形的其他实际应用
14.【答案】6
【知识点】解直角三角形
15.【答案】45.8米
【知识点】解直角三角形的实际应用﹣仰角俯角问题
16.【答案】25;
【知识点】解直角三角形—构造直角三角形
17.【答案】(1);
(2).
【知识点】特殊角的三角函数的混合运算
18.【答案】解:原式
.
【知识点】特殊角的三角函数的混合运算
19.【答案】任务一:;任务二:闸门没有打开;任务三:
【知识点】解直角三角形
20.【答案】米
【知识点】解直角三角形的其他实际应用
21.【答案】小山上古塔的高约为.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
22.【答案】解:延长CB交PQ于点D.
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵自动扶梯AB的坡度为1:2.4,
∴==.
设BD=5k米,AD=12k米,则AB=13k米.
∵AB=13米,
∴k=1,
∴BD=5米,AD=12米.
在Rt△CDA中,∠CDA=90゜,∠CAD=42°,
∴CD=AD tan∠CAD≈12×0.90≈10.8米,
∴BC≈5.8米.
答:二楼的层高BC约为5.8米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
23.【答案】解:距离烟囱东方35m远的一棵大树被歪倒的烟囱砸着. 理由如下:
∵ m,∠GCB=30°,∠ACG=45°,
∴ m,
∴
m,
∴ m,
∵ >35,
∴距离烟囱东方35m远的一棵大树被歪倒的烟囱砸着.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21世纪教育网(www.21cnjy.com)
1 / 10
同课章节目录
