7.2.3 平行线的性质 同步练习 2024--2025学年初中数学人教版七年级下册(新教材)
文档属性
| 名称 | 7.2.3 平行线的性质 同步练习 2024--2025学年初中数学人教版七年级下册(新教材) |  | |
| 格式 | docx | ||
| 文件大小 | 663.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 17:27:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
7.2.3 平行线的性质 同步练习
2024--2025学年初中数学人教版七年级下册(新教材)
一、单选题
1.如图,直线AB∥CD,MN分别与AB、CD交于点E、F,且∠AEM=50°,则∠DFN的大小为( )
A.130° B.60° C.50° D.40°
2.如图,直线,,,,则( )
A.45° B.55° C.65° D.75°
3.如图,AB∥CD,∠C=110°,∠B=120°,则∠BEC等于 ( )
A.110° B.120° C.130° D.150°
4.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若,则∠1的值( )
A.52° B.66° C.72° D.76°
5.如图,AB∥CD,且∠BAP=60°-α,∠APC=45°+α,∠PCD=30°-α,则α=( )
A.10° B.15° C.20° D.30°
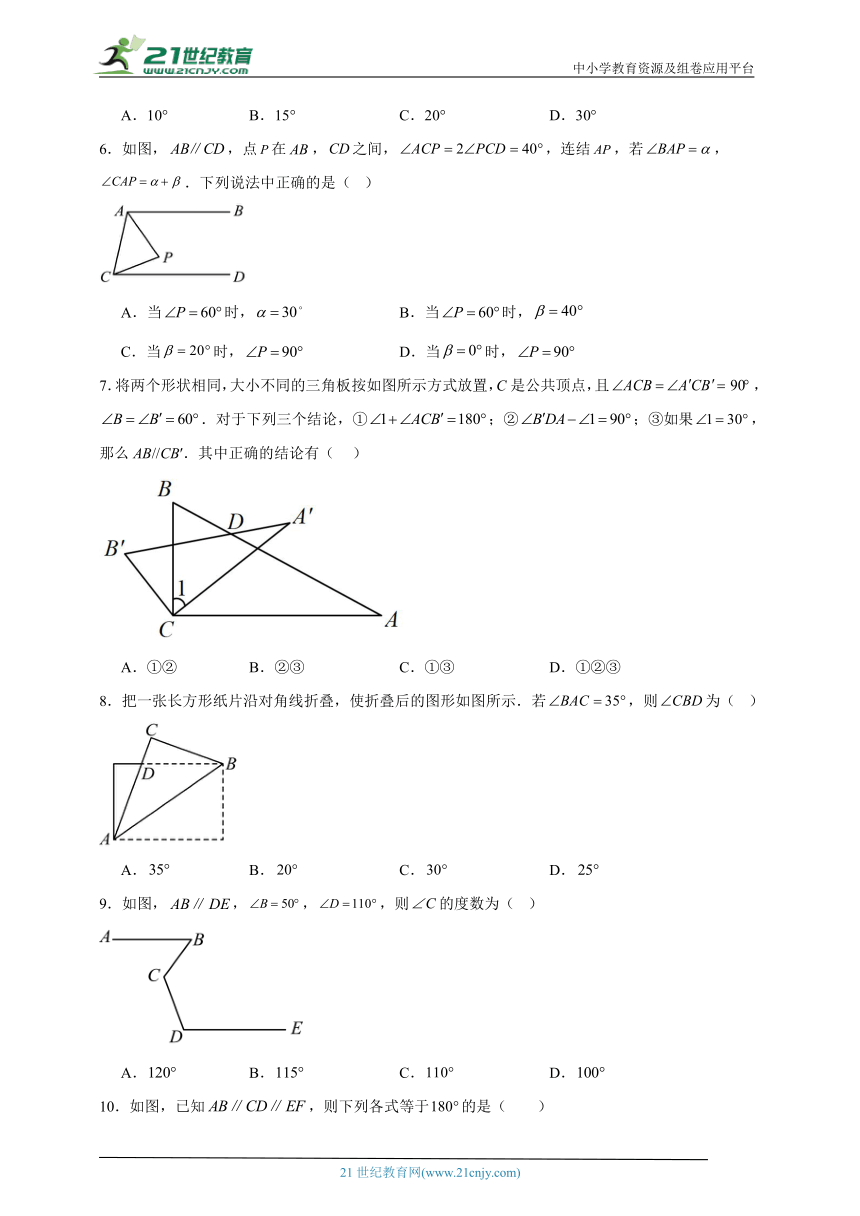
6.如图,,点在,之间,,连结,若,.下列说法中正确的是( )
A.当时, B.当时,
C.当时, D.当时,
7.将两个形状相同,大小不同的三角板按如图所示方式放置,C是公共顶点,且,.对于下列三个结论,①;②;③如果,那么AB//CB′.其中正确的结论有( )
A.①② B.②③ C.①③ D.①②③
8.把一张长方形纸片沿对角线折叠,使折叠后的图形如图所示.若,则为( )
A. B. C. D.
9.如图,,,,则的度数为( )
A. B. C. D.
10.如图,已知,则下列各式等于的是( )
A. B. C. D.
二、填空题
11.如图,AB∥CD,点E是CD上一点,∠AEC=40°,EF平分∠AED交AB于点F,则∠AFE= 度.
12.如图,a∥b,则∠A= .
13.如图,已知,,那么的度数为 .
14.如图, ,,,, 若, .
15.如图,已知,M为平行线之间一点,连接,N为上方一点,连接,E为延长线上一点,若分别平分,则∠M、∠N满足的关系式是
三、解答题
16.如图,已知:,试说明:.
17.阅读理解,补全证明过程及推理依据.
已知:如图,点E在直线上,点B在直线上,,.求证:.
证明:∵(已知)
(____________________)
∴(____________________)
∴(____________________)
∴+______=(____________________)
又∵(已知)
∴(等量代换)
∴______∥______(____________________)
∴(____________________)
18.阅读题目,完成下面推理过程.
问题:中国汉字博大精深,方块文字智慧灵秀,奥妙无穷.如图①是一个“互”字.如图②是由图①抽象的几何图形,其中,点在同一直线上,点在同一直线上,且.
求证:.
证明:如图(2),延长交于点.
(已知),
(_______)
又(_______),
_______(等量代换),
(_______),
(_______).
又(已知),
(两直线平行,同旁内角互补),
(_______).
参考答案
1.C
根据平行线得出性质求出∠CFE,根据对顶角相等得出即可.
解:∵AB∥CD,∠AEM=50°,
∴∠CFE=∠AEM=50°,
∴∠DFN=∠CFE=50°,
故选C.
2.D
解:∵∠1=∠3,
∴AB∥EF,
∵AB∥CD,
∴EF∥CD,
∴∠3=∠C=50°,∠FED=∠2=25°,
∴∠BED=∠3+∠FED=50°+25°=75°.
故选:D.
3.C
过点E作EF∥AB,如图所示:
∵AB∥CD,
∴EF∥AB∥CD,
∴∠1+∠B=180°,∠2+∠C=180°,
∵∠C=110°,∠B=120°,
∴∠1=60°,∠2=70°,
∴∠BEC=∠1+∠2=130°.
4.D
由折叠的性质可得:∠DEF=∠GEF,根据平行线的性质:两直线平行,内错角相等可得:∠DEF=∠EFG=52°,从而得到∠GEF=52°,根据平角的定义即可求得∠1.
∵长方形纸片ABCD,
∴AD∥BC,
∴∠DEF=∠EFG=52°,
∵把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,∠EFG=52°,
∴由折叠的性质可得:∠DEF=∠FEG=52°,
∴∠1=180°-∠GEF-∠DEF=180°-52°-52°=76°.
5.B
过点P作PM∥AB,
∴AB∥PM∥CD,
∴∠BAP=∠APM,∠DCP=∠MPC,
∴∠APC=∠APM+∠CPM=∠BAP+∠DCP,
∴45°+α=(60°-α)+(30°-α),
解得α=15°.
故选B.
6.B
解:过点作交于点,
,
,
,,.
,
,,
当时,
,
故A项错误,不符合题意;
,
又,
即,
,
故B项正确,符合题意;
当时,
,
,
,
,
;
故C项错误,不符合题意;
当时,
,
,
,
,
;
故D项错误,不符合题意;
故选:B.
7.D
如图,延长AC到点F,
根据邻补角的定义得:∠FCB′+∠ACB'=108°.
根据同角的余角相等得:∠FCB=∠1,
所以有∠1+∠ACB'=180°,
故①正确.
由“8”字形可得:∠A′DA+∠A′=∠A+∠A′CA,
∴180°-∠B'DA+30°=90°-∠1+30°,
∴∠B'DA-∠1=90°,
故②正确.
如果∠1=30°,则∠BCB′=60°=∠B.
∴AB∥CB'.
故③正确.
8.B
解:如图,由题意,得,,
,
,
,
,
故选:B.
9.A
过点作,由平行公理的推论可得,由两直线平行内错角相等可得,由两直线平行同旁内角互补可得,结合已知条件,,进而可得,,然后根据即可得出答案.
解:如图,过点作,
,
,
,,
,,
,,
,
故选:.
10.B
解:∵,
∴,
∴,
∴,
故选:B.
11.70°.
由平角求出∠AED的度数,由角平分线得出∠DEF的度数,再由平行线的性质即可求出∠AFE的度数.
∵∠AEC=40°,
∴∠AED=180°﹣∠AEC=140°,
∵EF平分∠AED,
∴,
又∵AB∥CD,
∴∠AFE=∠DEF=70°.
故答案为70
12.22°
如下图,过点A作AD∥b,则由已知可得AD∥a∥b,由此可得∠DAC=∠ACE=50°,∠DAB=∠ABF=28°,从而由∠BAC=∠DAC-∠DAB即可求得∠BAC的度数.
解:如下图,过点A作AD∥b,
∵a//b,
∴AD∥a∥b,
∴∠DAC=∠ACE=50°,∠DAB=∠ABF=28°,
∴∠BAC=∠DAC-∠DAB=50°-28°=22°.
故答案为:22°.
13./100度
此题考查了平行线的性质和判定,对顶角相等,
首先得到,证明出,然后得到,进而求解即可.
如图所示,
∵,
∴
∴
∴
∴.
故答案为:.
14.
解:∵,
∴,,
∵,
∴,
∴,
∵,
∴,
又∵,
∴,
∴,
∵,,,
∴.
故答案为:4.
15.
解:如图所示,过点M作,过点N作,
∵,
∴,
∴,
∴,
∵分别平分,
∴,
∵,
∴,
∵,
∴,
∴
,
即.
故答案为:.
16.见解析
解:如图,过点E作直线,使得,
因为,
所以.
因为,所以,
所以.
因为,
所以,
故.
17.见解析
证明:∵(已知),
(对顶角相等),
∴(等量代换),
∴(同位角相等,两直线平行),
∴(两直线平行,同旁内角互补),
又∵(已知),
∴,
∴(同旁内角互补,两直线平行),
∴(两直线平行,内错角相等).
故答案为:对顶角相等;等量代换;同位角相等,两直线平行;∠C;两直线平行,同旁内角互补; AC ;DF;同旁内角互补,两直线平行;两直线平行,内错角相等
18.两直线平行,内错角相等;已知;;同位角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等
证明:如图(2),延长交于点.
(已知),
(两直线平行,内错角相等)
又(已知),
(等量代换),
(同位角相等,两直线平行),
(两直线平行,同旁内角互补).
又(已知),
(两直线平行,同旁内角互补),
(同角的补角相等).
故答案为:两直线平行,内错角相等;;已知;;同位角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.2.3 平行线的性质 同步练习
2024--2025学年初中数学人教版七年级下册(新教材)
一、单选题
1.如图,直线AB∥CD,MN分别与AB、CD交于点E、F,且∠AEM=50°,则∠DFN的大小为( )
A.130° B.60° C.50° D.40°
2.如图,直线,,,,则( )
A.45° B.55° C.65° D.75°
3.如图,AB∥CD,∠C=110°,∠B=120°,则∠BEC等于 ( )
A.110° B.120° C.130° D.150°
4.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若,则∠1的值( )
A.52° B.66° C.72° D.76°
5.如图,AB∥CD,且∠BAP=60°-α,∠APC=45°+α,∠PCD=30°-α,则α=( )
A.10° B.15° C.20° D.30°
6.如图,,点在,之间,,连结,若,.下列说法中正确的是( )
A.当时, B.当时,
C.当时, D.当时,
7.将两个形状相同,大小不同的三角板按如图所示方式放置,C是公共顶点,且,.对于下列三个结论,①;②;③如果,那么AB//CB′.其中正确的结论有( )
A.①② B.②③ C.①③ D.①②③
8.把一张长方形纸片沿对角线折叠,使折叠后的图形如图所示.若,则为( )
A. B. C. D.
9.如图,,,,则的度数为( )
A. B. C. D.
10.如图,已知,则下列各式等于的是( )
A. B. C. D.
二、填空题
11.如图,AB∥CD,点E是CD上一点,∠AEC=40°,EF平分∠AED交AB于点F,则∠AFE= 度.
12.如图,a∥b,则∠A= .
13.如图,已知,,那么的度数为 .
14.如图, ,,,, 若, .
15.如图,已知,M为平行线之间一点,连接,N为上方一点,连接,E为延长线上一点,若分别平分,则∠M、∠N满足的关系式是
三、解答题
16.如图,已知:,试说明:.
17.阅读理解,补全证明过程及推理依据.
已知:如图,点E在直线上,点B在直线上,,.求证:.
证明:∵(已知)
(____________________)
∴(____________________)
∴(____________________)
∴+______=(____________________)
又∵(已知)
∴(等量代换)
∴______∥______(____________________)
∴(____________________)
18.阅读题目,完成下面推理过程.
问题:中国汉字博大精深,方块文字智慧灵秀,奥妙无穷.如图①是一个“互”字.如图②是由图①抽象的几何图形,其中,点在同一直线上,点在同一直线上,且.
求证:.
证明:如图(2),延长交于点.
(已知),
(_______)
又(_______),
_______(等量代换),
(_______),
(_______).
又(已知),
(两直线平行,同旁内角互补),
(_______).
参考答案
1.C
根据平行线得出性质求出∠CFE,根据对顶角相等得出即可.
解:∵AB∥CD,∠AEM=50°,
∴∠CFE=∠AEM=50°,
∴∠DFN=∠CFE=50°,
故选C.
2.D
解:∵∠1=∠3,
∴AB∥EF,
∵AB∥CD,
∴EF∥CD,
∴∠3=∠C=50°,∠FED=∠2=25°,
∴∠BED=∠3+∠FED=50°+25°=75°.
故选:D.
3.C
过点E作EF∥AB,如图所示:
∵AB∥CD,
∴EF∥AB∥CD,
∴∠1+∠B=180°,∠2+∠C=180°,
∵∠C=110°,∠B=120°,
∴∠1=60°,∠2=70°,
∴∠BEC=∠1+∠2=130°.
4.D
由折叠的性质可得:∠DEF=∠GEF,根据平行线的性质:两直线平行,内错角相等可得:∠DEF=∠EFG=52°,从而得到∠GEF=52°,根据平角的定义即可求得∠1.
∵长方形纸片ABCD,
∴AD∥BC,
∴∠DEF=∠EFG=52°,
∵把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,∠EFG=52°,
∴由折叠的性质可得:∠DEF=∠FEG=52°,
∴∠1=180°-∠GEF-∠DEF=180°-52°-52°=76°.
5.B
过点P作PM∥AB,
∴AB∥PM∥CD,
∴∠BAP=∠APM,∠DCP=∠MPC,
∴∠APC=∠APM+∠CPM=∠BAP+∠DCP,
∴45°+α=(60°-α)+(30°-α),
解得α=15°.
故选B.
6.B
解:过点作交于点,
,
,
,,.
,
,,
当时,
,
故A项错误,不符合题意;
,
又,
即,
,
故B项正确,符合题意;
当时,
,
,
,
,
;
故C项错误,不符合题意;
当时,
,
,
,
,
;
故D项错误,不符合题意;
故选:B.
7.D
如图,延长AC到点F,
根据邻补角的定义得:∠FCB′+∠ACB'=108°.
根据同角的余角相等得:∠FCB=∠1,
所以有∠1+∠ACB'=180°,
故①正确.
由“8”字形可得:∠A′DA+∠A′=∠A+∠A′CA,
∴180°-∠B'DA+30°=90°-∠1+30°,
∴∠B'DA-∠1=90°,
故②正确.
如果∠1=30°,则∠BCB′=60°=∠B.
∴AB∥CB'.
故③正确.
8.B
解:如图,由题意,得,,
,
,
,
,
故选:B.
9.A
过点作,由平行公理的推论可得,由两直线平行内错角相等可得,由两直线平行同旁内角互补可得,结合已知条件,,进而可得,,然后根据即可得出答案.
解:如图,过点作,
,
,
,,
,,
,,
,
故选:.
10.B
解:∵,
∴,
∴,
∴,
故选:B.
11.70°.
由平角求出∠AED的度数,由角平分线得出∠DEF的度数,再由平行线的性质即可求出∠AFE的度数.
∵∠AEC=40°,
∴∠AED=180°﹣∠AEC=140°,
∵EF平分∠AED,
∴,
又∵AB∥CD,
∴∠AFE=∠DEF=70°.
故答案为70
12.22°
如下图,过点A作AD∥b,则由已知可得AD∥a∥b,由此可得∠DAC=∠ACE=50°,∠DAB=∠ABF=28°,从而由∠BAC=∠DAC-∠DAB即可求得∠BAC的度数.
解:如下图,过点A作AD∥b,
∵a//b,
∴AD∥a∥b,
∴∠DAC=∠ACE=50°,∠DAB=∠ABF=28°,
∴∠BAC=∠DAC-∠DAB=50°-28°=22°.
故答案为:22°.
13./100度
此题考查了平行线的性质和判定,对顶角相等,
首先得到,证明出,然后得到,进而求解即可.
如图所示,
∵,
∴
∴
∴
∴.
故答案为:.
14.
解:∵,
∴,,
∵,
∴,
∴,
∵,
∴,
又∵,
∴,
∴,
∵,,,
∴.
故答案为:4.
15.
解:如图所示,过点M作,过点N作,
∵,
∴,
∴,
∴,
∵分别平分,
∴,
∵,
∴,
∵,
∴,
∴
,
即.
故答案为:.
16.见解析
解:如图,过点E作直线,使得,
因为,
所以.
因为,所以,
所以.
因为,
所以,
故.
17.见解析
证明:∵(已知),
(对顶角相等),
∴(等量代换),
∴(同位角相等,两直线平行),
∴(两直线平行,同旁内角互补),
又∵(已知),
∴,
∴(同旁内角互补,两直线平行),
∴(两直线平行,内错角相等).
故答案为:对顶角相等;等量代换;同位角相等,两直线平行;∠C;两直线平行,同旁内角互补; AC ;DF;同旁内角互补,两直线平行;两直线平行,内错角相等
18.两直线平行,内错角相等;已知;;同位角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等
证明:如图(2),延长交于点.
(已知),
(两直线平行,内错角相等)
又(已知),
(等量代换),
(同位角相等,两直线平行),
(两直线平行,同旁内角互补).
又(已知),
(两直线平行,同旁内角互补),
(同角的补角相等).
故答案为:两直线平行,内错角相等;;已知;;同位角相等,两直线平行;两直线平行,同旁内角互补;同角的补角相等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
