7.2.2 平行线的判定 同步练习 2024--2025学年初中数学人教版七年级下册(新教材)
文档属性
| 名称 | 7.2.2 平行线的判定 同步练习 2024--2025学年初中数学人教版七年级下册(新教材) |  | |
| 格式 | docx | ||
| 文件大小 | 613.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 17:27:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
7.2.2 平行线的判定 同步练习
2024--2025学年初中数学人教版七年级下册(新教材)
一、单选题
1.如图,下列条件中,不能判定的是( )
A. B.
C. D.
2.将文具套尺中的量角器和三角板按照如图方式摆放,其中,三角板的直角顶点C与量角器的中心重合,为量角器的直径.下列条件中,不能判定的是()
A. B.
C. D.
3.如图,直线,被直线所截,给出下列条件:①;②;③;④.其中能判定的是( )
A.①③ B.②④ C.①③④ D.①②③④
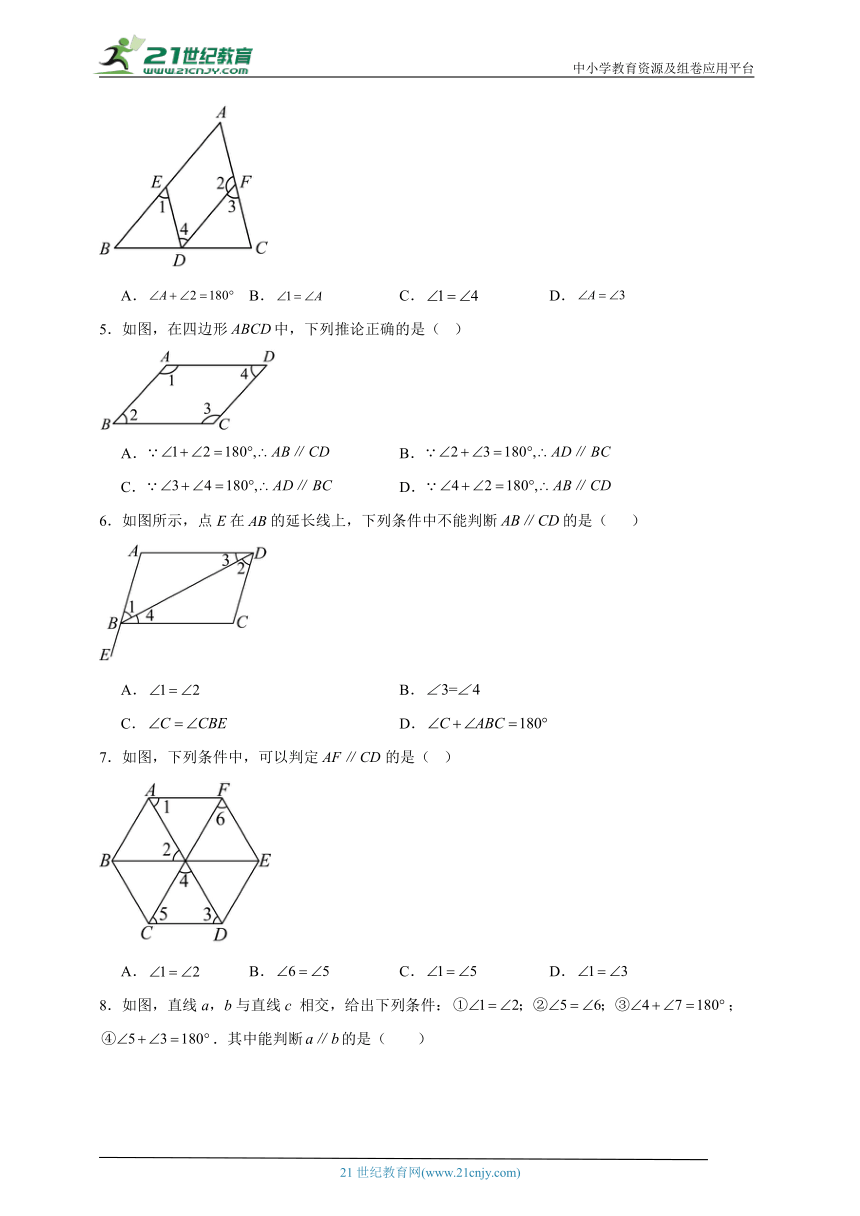
4.如图,下列条件,不能判定的是( )
A. B. C. D.
5.如图,在四边形中,下列推论正确的是( )
A. B.
C. D.
6.如图所示,点E在的延长线上,下列条件中不能判断的是( )
A. B.
C. D.
7.如图,下列条件中,可以判定的是( )
A. B. C. D.
8.如图,直线a,b与直线c 相交,给出下列条件:;.其中能判断的是( )
A.①②③④ B.①③④ C.①③ D.②④
二、填空题
9.如图是小明探索直线平行的条件时所用的学具,木条a,b,c在同一平面内.经测量,要使木条,则的度数应为 .
10.如图,当 时,.
11.如图,已知,则 ∥ ,理由是
12.如图,点E在的延长线上,若,则平行的是: .
13.小泽在课桌上摆放了一副三角板,如图所示,得到,依据是 .
14.如图,一条公路的两个拐角和若,要使公路和在同一方向上,需要使 度,依据是 .
三、解答题
15.如图,,直线与平行吗?为什么?
16.如图,直线,被直线所截,平分,,.求证:.
17.如图,已知直线a,b,c被d所截,且,.试说明:.
解:因为(已知)
(___________)
所以___________=___________(等量代换)
所以______________________(___________)
又因为(已知)
所以______________________(___________)
18.完成下面的证明:
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,求证:AB∥CD.
证明:∵BE平分∠ABD ( )
∴∠ABD=2∠α ( )
∵DE平分∠BDC(已知)
∵∠BDC= ( )
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β) ( )
∵∠α+∠β=90°(已知)
∴∠ABD+∠BDC=( )
∴ AB∥CD ( )
参考答案
1.D
解:因为,所以,故A不符合题意;
因为,所以,故B不符合题意;
因为,所以,故C不符合题意;
因为,所以,故D符合题意.
故选:D.
2.D
解:
,
故A不符合题意;
,
,
,
故B不符合题意;
,
,
故C不符合题意;
由不能得出,
故D符合题意;
故选:D.
3.D
解:∵,
∴,故①正确;
∵,
∴,故②正确;
∵,
又∵,
∴,
∴,故③正确;
∵,,
又∵,
∴,
∴,故④正确,
综上可得:能判断的条件是①②③④.
故选:D.
4.B
解:A、由,可以根据同旁内角互补,两直线平行得到,故此选项不符合题意;
B、由,可以根据同位角相等,两直线平行得到,不可以得到,故此选项符合题意;
C、由,可以根据内错角相等,两直线平行得到,故此选项不符合题意;
D、由,可以根据同位角相等,两直线平行得到,故此选项不符合题意;
故选:B.
5.C
解:,故A选项错误;
,故B选项错误;
,故C选项正确;
,无法推出或,故D选项错误.
故选:C.
6.B
A、∵和是、被所截得到的一对内错角,∴当时,可得,故此选项不符合题意;
B、∵和是、被所截得到的一对内错角,∴当时,可得,故此选项符合题意;
C、∵和是、被所截得到的一对内错角,∴当时,可得,故此选项不符合题意;
D、∵和是、被所截得到的一对同旁内角,∴当时,可得,故此选项不符合题意.
故选:B.
7.D
解:A、不能判定,故本选项不符合题意;
B、不能判定,故本选项不符合题意;
C、不能判定,故本选项不符合题意;
D、能判定,故本选项符合题意;
故选:D
8.B
解:
∴,故①符合题意;
和是对顶角,根据不能判定,故②不符合题意;
,
∴,故③符合题意;
∴,故④符合题意;
综上,①③④能判定,
故选:B.
9./70度
解:当时,则,
∴,
故答案为:
10./
解:依题意,则
故答案为:
11. 同位角相等,两直线平行
解:∵
∴
∴(同位角相等,两直线平行)
故答案为:;;同位角相等,两直线平行.
12.
本题主要考查了平行线的判定,根据内错角相等,两直线平行即可得到答案.
解:∵,
∴,
故答案为:.
13.内错角相等,两直线平行
本题考查了平行线的判定.熟练掌握平行线的判定是解题的关键.
根据平行线的判定作答即可.
解:由题意知,,
∴(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
14. 内错角相等,两直线平行
平行,可得.
解:要使公路和在同一方向上,即,
当时,
依据是内错角相等,两直线平行,
故答案为:内错角相等,两直线平行
15.,理由见解析
解:理由如下:
∵(已知),(对顶角相等),
∴(等量代换).
∵(已知),(平角定义),
∴,
又∵(已知),
∴(等量代换),
∴(同位角相等、两直线平行).
16.见解析.
根据角平分线的定义,可证得,结合,即可证明结论.
∵平分,,
∴.
又,
∴.
∴.
17.对顶角相等,2,3,a,c,同位角相等,两直线平行,b,c,平行于同一直线的两条直线互相平行
解:因为(已知)
(对顶角相等)
所以2=3(等量代换)
所以ac(同位角相等,两直线平行)
又因为(已知)
所以bc(平行于同一直线的两条直线互相平行)
18.已知;角平分线的定义;2∠β ;角平分线的定义;等量代换;180°;同旁内角互补两直线平行
首先根据角平分线的定义可得∠ABD=2∠α,∠BDC=2∠β,根据等量代换可得∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β),进而得到∠ABD+∠BDC=180°,然后再根据同旁内角互补两直线平行可得答案.
解:∵BE平分∠ABD (已知),
∴∠ABD=2∠α(角平分线的定义).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (角平分线的定义),
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)(等量代换),
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°,
∴AB∥CD(同旁内角互补两直线平行).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.2.2 平行线的判定 同步练习
2024--2025学年初中数学人教版七年级下册(新教材)
一、单选题
1.如图,下列条件中,不能判定的是( )
A. B.
C. D.
2.将文具套尺中的量角器和三角板按照如图方式摆放,其中,三角板的直角顶点C与量角器的中心重合,为量角器的直径.下列条件中,不能判定的是()
A. B.
C. D.
3.如图,直线,被直线所截,给出下列条件:①;②;③;④.其中能判定的是( )
A.①③ B.②④ C.①③④ D.①②③④
4.如图,下列条件,不能判定的是( )
A. B. C. D.
5.如图,在四边形中,下列推论正确的是( )
A. B.
C. D.
6.如图所示,点E在的延长线上,下列条件中不能判断的是( )
A. B.
C. D.
7.如图,下列条件中,可以判定的是( )
A. B. C. D.
8.如图,直线a,b与直线c 相交,给出下列条件:;.其中能判断的是( )
A.①②③④ B.①③④ C.①③ D.②④
二、填空题
9.如图是小明探索直线平行的条件时所用的学具,木条a,b,c在同一平面内.经测量,要使木条,则的度数应为 .
10.如图,当 时,.
11.如图,已知,则 ∥ ,理由是
12.如图,点E在的延长线上,若,则平行的是: .
13.小泽在课桌上摆放了一副三角板,如图所示,得到,依据是 .
14.如图,一条公路的两个拐角和若,要使公路和在同一方向上,需要使 度,依据是 .
三、解答题
15.如图,,直线与平行吗?为什么?
16.如图,直线,被直线所截,平分,,.求证:.
17.如图,已知直线a,b,c被d所截,且,.试说明:.
解:因为(已知)
(___________)
所以___________=___________(等量代换)
所以______________________(___________)
又因为(已知)
所以______________________(___________)
18.完成下面的证明:
如图,BE平分∠ABD,DE平分∠BDC,且∠α+∠β=90°,求证:AB∥CD.
证明:∵BE平分∠ABD ( )
∴∠ABD=2∠α ( )
∵DE平分∠BDC(已知)
∵∠BDC= ( )
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β) ( )
∵∠α+∠β=90°(已知)
∴∠ABD+∠BDC=( )
∴ AB∥CD ( )
参考答案
1.D
解:因为,所以,故A不符合题意;
因为,所以,故B不符合题意;
因为,所以,故C不符合题意;
因为,所以,故D符合题意.
故选:D.
2.D
解:
,
故A不符合题意;
,
,
,
故B不符合题意;
,
,
故C不符合题意;
由不能得出,
故D符合题意;
故选:D.
3.D
解:∵,
∴,故①正确;
∵,
∴,故②正确;
∵,
又∵,
∴,
∴,故③正确;
∵,,
又∵,
∴,
∴,故④正确,
综上可得:能判断的条件是①②③④.
故选:D.
4.B
解:A、由,可以根据同旁内角互补,两直线平行得到,故此选项不符合题意;
B、由,可以根据同位角相等,两直线平行得到,不可以得到,故此选项符合题意;
C、由,可以根据内错角相等,两直线平行得到,故此选项不符合题意;
D、由,可以根据同位角相等,两直线平行得到,故此选项不符合题意;
故选:B.
5.C
解:,故A选项错误;
,故B选项错误;
,故C选项正确;
,无法推出或,故D选项错误.
故选:C.
6.B
A、∵和是、被所截得到的一对内错角,∴当时,可得,故此选项不符合题意;
B、∵和是、被所截得到的一对内错角,∴当时,可得,故此选项符合题意;
C、∵和是、被所截得到的一对内错角,∴当时,可得,故此选项不符合题意;
D、∵和是、被所截得到的一对同旁内角,∴当时,可得,故此选项不符合题意.
故选:B.
7.D
解:A、不能判定,故本选项不符合题意;
B、不能判定,故本选项不符合题意;
C、不能判定,故本选项不符合题意;
D、能判定,故本选项符合题意;
故选:D
8.B
解:
∴,故①符合题意;
和是对顶角,根据不能判定,故②不符合题意;
,
∴,故③符合题意;
∴,故④符合题意;
综上,①③④能判定,
故选:B.
9./70度
解:当时,则,
∴,
故答案为:
10./
解:依题意,则
故答案为:
11. 同位角相等,两直线平行
解:∵
∴
∴(同位角相等,两直线平行)
故答案为:;;同位角相等,两直线平行.
12.
本题主要考查了平行线的判定,根据内错角相等,两直线平行即可得到答案.
解:∵,
∴,
故答案为:.
13.内错角相等,两直线平行
本题考查了平行线的判定.熟练掌握平行线的判定是解题的关键.
根据平行线的判定作答即可.
解:由题意知,,
∴(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
14. 内错角相等,两直线平行
平行,可得.
解:要使公路和在同一方向上,即,
当时,
依据是内错角相等,两直线平行,
故答案为:内错角相等,两直线平行
15.,理由见解析
解:理由如下:
∵(已知),(对顶角相等),
∴(等量代换).
∵(已知),(平角定义),
∴,
又∵(已知),
∴(等量代换),
∴(同位角相等、两直线平行).
16.见解析.
根据角平分线的定义,可证得,结合,即可证明结论.
∵平分,,
∴.
又,
∴.
∴.
17.对顶角相等,2,3,a,c,同位角相等,两直线平行,b,c,平行于同一直线的两条直线互相平行
解:因为(已知)
(对顶角相等)
所以2=3(等量代换)
所以ac(同位角相等,两直线平行)
又因为(已知)
所以bc(平行于同一直线的两条直线互相平行)
18.已知;角平分线的定义;2∠β ;角平分线的定义;等量代换;180°;同旁内角互补两直线平行
首先根据角平分线的定义可得∠ABD=2∠α,∠BDC=2∠β,根据等量代换可得∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β),进而得到∠ABD+∠BDC=180°,然后再根据同旁内角互补两直线平行可得答案.
解:∵BE平分∠ABD (已知),
∴∠ABD=2∠α(角平分线的定义).
∵DE平分∠BDC(已知),
∴∠BDC=2∠β (角平分线的定义),
∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)(等量代换),
∵∠α+∠β=90°(已知),
∴∠ABD+∠BDC=180°,
∴AB∥CD(同旁内角互补两直线平行).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
