2024-2025学年广东省深圳市坪山区八年级(上)期末数学试卷(含详解)
文档属性
| 名称 | 2024-2025学年广东省深圳市坪山区八年级(上)期末数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-21 18:52:47 | ||
图片预览




文档简介
2024-2025学年广东省深圳市坪山区八年级(上)期末数学试卷
一、选择题:(本大题8个小题,每小题3分,共24分)
1.(3分)f(x)=ex是一个数学函数,它表示自然数e的指数次幂.其中自然数e是一个无理数(e=2.718281828459045 )则在下列实数中,( )也是无理数
A. B. C.3.14 D.
2.(3分)下列计算中,正确的是( )
A. B. C. D.
3.(3分)若a,b,c是三角形的三边长,则满足下列条件的a,b,c不能构成直角三角形的是( )
A.a=1,b=1,c=2 B.a=b=5,c=5
C.a:b:c=3:4:5 D.a=5,b=13,c=12
4.(3分)函数y=﹣2x+1的图象一定经过下列四个点中的( )
A.(1,﹣3) B.(﹣2,4) C.(﹣1,1) D.(0,1)
5.(3分)科技是第一生产力,创新是第一动力,教育、科技、人才是全面建设社会主义现代化国家的基础性、战略性支撑.某校准备从甲、乙、丙、丁四个科技小组中选出一组,参加坪山区中小学科技创新竞赛,如表记录了各组平时成绩的平均数(单位:分)及方差.若要选出一个成绩好且状态稳定的小组去参加比赛,则应选择的小组是( )
甲 乙 丙 丁
平均数 93 97 97 95
方差 0.8 0.8 1.2 1.2
A.甲 B.乙 C.丙 D.丁
6.(3分)某粮食生产专业户去年计划生产水稻和小麦共18t,实际生产了20t,其中水稻超产15%,小麦超产10%,问:该专业户去年计划生产水稻、小麦各多少吨?设该专业户去年计划生产水稻x吨,小麦y吨,则下列方程组正确的是( )
A.
B.
C.
D.
7.(3分)如图,在△ABC中,∠B=56°,∠C=37°,AD和AE分别是△ABC的高和角平分线,则∠DAE的度数为( )
A.7.5° B.8.5° C.9.5° D.10.5°
8.(3分)已知直线l1:y=kx+b与直线都经过,直线l1交x轴于点A,交y轴于点B(0,4),直线l2交y轴于点C,交x轴于点D.直线l3∥直线l1且经过原点,且与直线l2交于点F,点P为x轴上任意一点,连接PC、PF.对于以下结论,错误的是( )
A.方程组的解为
B.S△OFD=3
C.△AED为直角三角形
D.当PF+PC的值最小时,点P的坐标为
二、填空题:(本大题5个小题,每小题3分,共15分)
9.(3分)8的立方根是 .
10.(3分)在坪山区某校文学节演讲比赛中,甲的演讲内容、演讲能力、演讲效果成绩如表所示:
项目 演讲内容 演讲能力 演讲效果
成绩/分 80 90 80
若按照演讲内容占60%,演讲能力占20%,演讲效果占20%,计算选手的综合成绩,则该选手的综合成绩为 分.
11.(3分)如图,△ABC中,∠ABC和∠ACB的角平分线BE与CF相交于点O,∠A=58°,则∠BOC为 °.
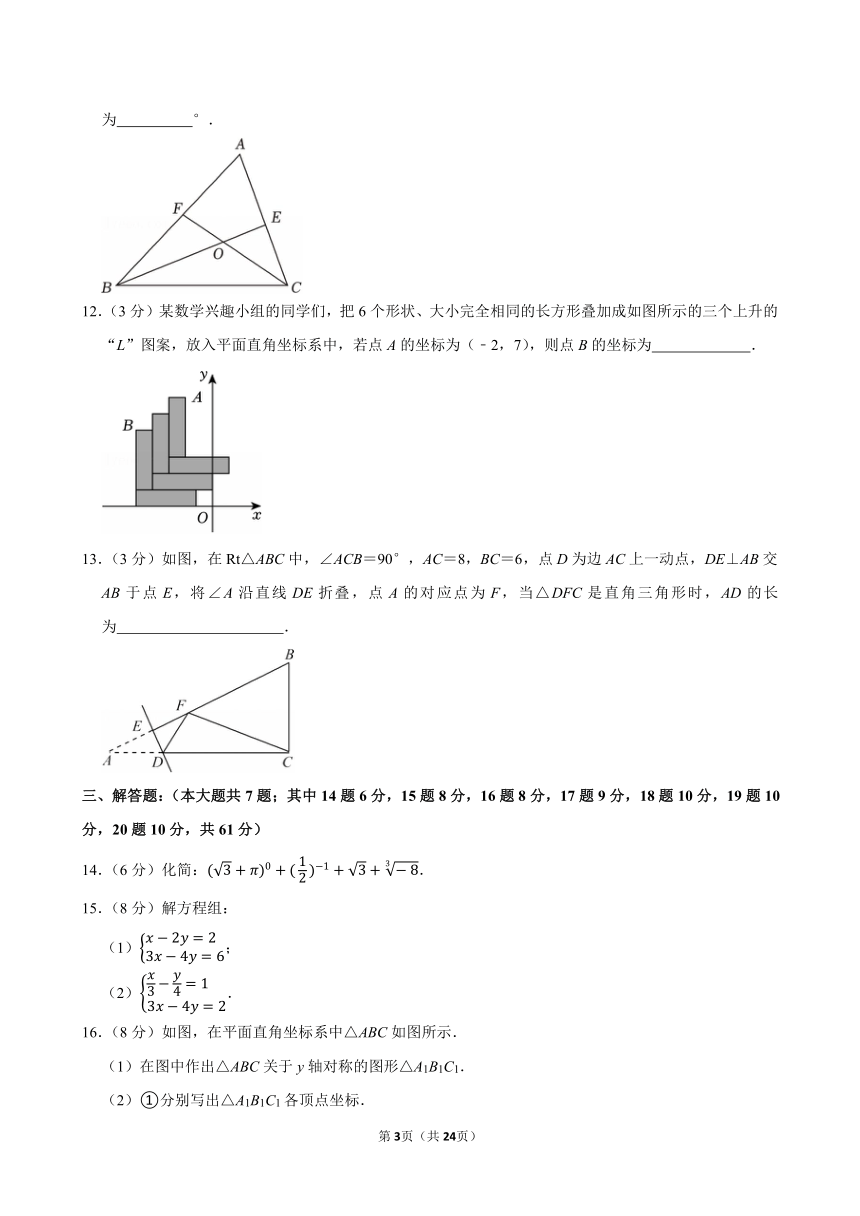
12.(3分)某数学兴趣小组的同学们,把6个形状、大小完全相同的长方形叠加成如图所示的三个上升的“L”图案,放入平面直角坐标系中,若点A的坐标为(﹣2,7),则点B的坐标为 .
13.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D为边AC上一动点,DE⊥AB交AB于点E,将∠A沿直线DE折叠,点A的对应点为F,当△DFC是直角三角形时,AD的长为 .
三、解答题:(本大题共7题;其中14题6分,15题8分,16题8分,17题9分,18题10分,19题10分,20题10分,共61分)
14.(6分)化简:.
15.(8分)解方程组:
(1);
(2).
16.(8分)如图,在平面直角坐标系中△ABC如图所示.
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1.
(2)①分别写出△A1B1C1各顶点坐标.
②求△A1B1C1的面积.
(3)若以B点为圆心,AB的长为半径作弧线,交射线BB1于点E,请在图中作出线段BE(留下作图痕迹),并求出E点的坐标.
17.(9分)近年来,新能源汽车扎根坪山、立足深圳、放眼全球,通过一路自主创新,发展加速狂飙.坪山区作为深圳打造“新一代世界一流汽车城”的核心承载区,新能源汽车消费市场有巨大的发展潜力,因此坪山区居民对电车充电桩的需求也在不断增加,目前公共充电桩的收费方式有:按电量计费、按时间计费、按峰谷计费,为了解调整充电桩收费方式的社会反响,新能源汽车工厂相关负责人随机访问了坪山区的部分车主,就“每月每部车的用电量”和“认为公共充电桩该如何收费”两个问题进行调查,并把调查结果整理成下面的图1,图2.(其中图1每月每部车用电范围为150~450千瓦时)
收费方式 收费标准
按电量计费 1.2元/千瓦时
按时间计费 2元/小时
按峰谷计费 10:00﹣19:00(低峰期,0.9元/千瓦时) 19:00﹣次日10:00(高峰期,1.5元/千瓦时)
在所有受调查的车主中共有1050位车主认为充电桩应该“按电量计费”,根据负责人绘制的图表和发现的信息,完成下列问题:
(1)n= ,负责人共调查了 位车主,并补全图1;
(2)如果坪山区有96000位车主,请你估计坪山区内认为充电桩收费应该“按峰谷计费”的车主数有多少?
(3)据了解深深的爸爸居住在坪山区,每天需要开电车往返于公司上班,已知他每个月电车耗电量范围落在图1的中位数 千瓦时,且他一般是在每天的12:00﹣20:00充电,如果你是深深的爸爸,结合以上信息,请分别从两个角度考虑:该选哪种计费方式的充电桩给电车充电?并说明理由(理由充分即可).
18.(10分)【教材呈现】
将正方形的四个顶点用线段连接,什么样的连法最短?研究发现,并非对角线最短,而是如图所示的连法最短(即用线段AE、DE、EF、BF、CF把四个顶点连接起来).已知如图1:∠DAE=∠ADE=30°,∠AEF=∠BFE=120°.
(1)由图1可知,线段AB和EF的位置关系为: ;
【问题探究】
(2)某数学兴趣小组发现,图1所示图形 (是/不是)轴对称图形,于是他们如图2构造了△AF′D≌△BFC,发现△AF′E是 三角形,请结合以上结论,猜想线段AE与OE的数量关系,并证明.
【问题解决】
(3)在第(2)问的基础上,若AB=6,求最短连法的线段和,即AE+DE+EF+BF+CF的值.
19.(10分)请根据以下素材,完成探究任务.
关于出票问题的探究
素材1 为提升市民审美品味和高雅文化消费,位于坪山文化聚落的坪山大剧院,每月都会在综合剧场(可容纳1200名观众)上演高品质的若干场剧目.按文化和旅游部的相关规定,剧院等演出场所的上座率(100%)原则上不得超过75%.
素材2 “每月一剧”惠民计划:为进一步提升辖区居民的幸福感,丰富居民群众的精神文化生活,坪山街道新和社区通过民生微实事项目平台,联合坪山大剧院联手推出惠民观剧活动,辖区居民只需40元即可购买一张当月上演的一场剧目前往观剧,数量有限,先购先得!
素材3 2024年11月的一场话剧推出A、B两种观赏票价,并参与“每月一剧”惠民购票活动.已知A种票10张、B种票5张、惠民票5张,共需3900元;购买2张B种票比购买1张A种票多出的费用,可购得惠民票2张.
问题解决
任务1 据悉,该话剧深受广大市民欢迎,上座人数恰好达到相关规定的上限,则观剧人数有 人.
任务2 设该话剧A种票价a元,B种票价b元,求出该话剧的A种、B种票价.
任务3 若A种票的持票人数y与B种票的持票人数x满足如图所示函数图象(其中x取正整数).请写出该场话剧票务收入W与x的函数表达式,求出该场话剧的最大票务收入.
20.(10分)折纸是一种以纸张折成各种不同形状的艺术活动,它是中国非物质文化遗产之一,具有悠久的历史和丰富的文化内涵.在现代,折纸艺术得到了进一步的发展和创新,材料已不只限于使用纸张,而且它还与自然科学结合在一起,发展出了折纸几何学,成为现代几何学的一个分支,形成有趣的“折纸数学”.
某校八年级一数学学习兴趣小组准备参加区数学创新能力大赛,他们尝试用一张直角三角形纸片探究折纸中的几何问题.
如图,他们准备了一张直角三角形纸片,记为Rt△ABC,∠C=90°,BC=3,AC=4.点P在线段AC上,将△ABP沿着直线BP翻折,点A落在点D处,BD交AC于点E.
【操作一】
如图1,小组成员甲将纸片折叠,使AP⊥DP,观察发现△BCP的形状是 ,此时AP为 ;
【操作二】
如图2,小组成员乙将纸片折叠,使AB与CB重叠,观察图形,请帮他求出△ADP的面积;
【操作三】
如图3,小组成员丙在图2的基础上,尝试在线段BC和AB上添加两个动点M、N,连接PM、MN,你能判断在M、N的运动过程中PM+MN是否存在最小值吗?如存在请求出PM+MN的最小值.
2024-2025学年广东省深圳市坪山区八年级(上)期末数学试卷
参考答案与试题解析
题号 1 2 3 4 5 6 7 8
答案 D C A D B A C B
一、选择题:(本大题8个小题,每小题3分,共24分)
1.(3分)f(x)=ex是一个数学函数,它表示自然数e的指数次幂.其中自然数e是一个无理数(e=2.718281828459045 )则在下列实数中,( )也是无理数
A. B. C.3.14 D.
【解答】解:根据无理数的定义可得,是无理数.
故选:D.
2.(3分)下列计算中,正确的是( )
A. B. C. D.
【解答】解:与不是同类项,不能进一步计算,
故A选项不正确,不符合题意;
4与不是同类项,不能进一步计算,
故B选项不正确,不符合题意;
,
故C选项正确,符合题意;
与3不是同类项,不能进一步计算,
故D选项不正确,不符合题意.
故选:C.
3.(3分)若a,b,c是三角形的三边长,则满足下列条件的a,b,c不能构成直角三角形的是( )
A.a=1,b=1,c=2 B.a=b=5,c=5
C.a:b:c=3:4:5 D.a=5,b=13,c=12
【解答】解:A、1+1=2,12+12≠22,不能构成直角三角形,符合题意;
B、52+52=(5)2,能构成直角三角形,不符合题意;
C、设a=3x,则b=4x,c=5x,
(3x)2+(4x)2=(5x)2,即a2+b2=c2,能构成直角三角形,不符合题意;
D、52+122=132,能构成直角三角形,不符合题意,
故选:A.
4.(3分)函数y=﹣2x+1的图象一定经过下列四个点中的( )
A.(1,﹣3) B.(﹣2,4) C.(﹣1,1) D.(0,1)
【解答】解:A、当x=1时,y=﹣1,故函数y=﹣2x+1的图象不经过(1,﹣3),不符合题意;
B、当x=﹣2时,y=5,故函数y=﹣2x+1的图象不经过(﹣2,4),不符合题意;
C、当x=﹣1时,y=3,故函数y=﹣2x+1的图象不经过(﹣1,1),不符合题意;
D、当x=0时,y=1,故函数y=﹣2x+1的图象经过(0,1),符合题意;
故选:D.
5.(3分)科技是第一生产力,创新是第一动力,教育、科技、人才是全面建设社会主义现代化国家的基础性、战略性支撑.某校准备从甲、乙、丙、丁四个科技小组中选出一组,参加坪山区中小学科技创新竞赛,如表记录了各组平时成绩的平均数(单位:分)及方差.若要选出一个成绩好且状态稳定的小组去参加比赛,则应选择的小组是( )
甲 乙 丙 丁
平均数 93 97 97 95
方差 0.8 0.8 1.2 1.2
A.甲 B.乙 C.丙 D.丁
【解答】解:∵乙的平均数最大,方差最小,
∴乙成绩好且状态稳定,
故选:B.
6.(3分)某粮食生产专业户去年计划生产水稻和小麦共18t,实际生产了20t,其中水稻超产15%,小麦超产10%,问:该专业户去年计划生产水稻、小麦各多少吨?设该专业户去年计划生产水稻x吨,小麦y吨,则下列方程组正确的是( )
A.
B.
C.
D.
【解答】解:由题意得,.
故选:A.
7.(3分)如图,在△ABC中,∠B=56°,∠C=37°,AD和AE分别是△ABC的高和角平分线,则∠DAE的度数为( )
A.7.5° B.8.5° C.9.5° D.10.5°
【解答】解:在△ABC中,∠B=56°,∠C=37°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣56°﹣37°=87°,
∵AE是△ABC的角平分线,
∴∠BAE43.5°,
∵AD是△ABC的高,
∴∠ADB=90°,
∵∠B=56°,
∴∠BAD=90°﹣∠B=90°﹣56°=34°,
∴∠DAE=∠BAE﹣∠BAD=43.5°﹣34°=9.5°,
故选:C.
8.(3分)已知直线l1:y=kx+b与直线都经过,直线l1交x轴于点A,交y轴于点B(0,4),直线l2交y轴于点C,交x轴于点D.直线l3∥直线l1且经过原点,且与直线l2交于点F,点P为x轴上任意一点,连接PC、PF.对于以下结论,错误的是( )
A.方程组的解为
B.S△OFD=3
C.△AED为直角三角形
D.当PF+PC的值最小时,点P的坐标为
【解答】解:A、∵直线l1:y=kx+b与直线都经过,
∴方程组的解为,故不符合题意;
B、把,点B(0,4)代入y=kx+b得,
∴,
∴直线l1:y=2x+4,
∵直线l3∥直线l1且经过原点,
∴直线l3的解析式为y=2x,
把代入yx+m得,m,
∴m=2,
∴直线l2:y,
解得,
∴F(,),
在y中,令y=0,则x+2=0,
解得x=4,
∴D(4,0),
∴S△OFD,故符合题意;
C、在y=2x+4中,令y=0,则2x+4=0,
∴x=﹣2,
∴A(﹣2,0),
∴AE2=(﹣2)2,DE2=(4)2,AD2=(﹣2﹣4)2=36,
∴AE2+DE2=AD2,
∴∠AED=90°,
∴△AED为直角三角形;不符合题意;
D、∵直线l2交y轴于点C,
∴C(0,2),
作点C故x轴的对称点C′,连接C′F交x轴于P,
此时,PF+PC的值最小,
设直线C′P的解析式为y=mx+n,
∵C′(0,﹣2),
∴,
∴
∴直线C′P的解析式为yx﹣2,
当y=0时,x,
∴P(,0),不符合题意;
故选:B.
二、填空题:(本大题5个小题,每小题3分,共15分)
9.(3分)8的立方根是 2 .
【解答】解:∵23=8,
∴8的立方根是2.
故答案为:2.
10.(3分)在坪山区某校文学节演讲比赛中,甲的演讲内容、演讲能力、演讲效果成绩如表所示:
项目 演讲内容 演讲能力 演讲效果
成绩/分 80 90 80
若按照演讲内容占60%,演讲能力占20%,演讲效果占20%,计算选手的综合成绩,则该选手的综合成绩为 82 分.
【解答】解:该选手的综合成绩为:80×60%+90×20%+80×20%=82(分),
故答案为:82.
11.(3分)如图,△ABC中,∠ABC和∠ACB的角平分线BE与CF相交于点O,∠A=58°,则∠BOC为 119 °.
【解答】解:在△ABC中,∠A=58°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣58°=122°,
∵∠ABC和∠ACB的角平分线BE与CF相交于点O,
∴∠OBC,∠OCBACB,
∴∠OBC+∠OCB122°=61°,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣61°=119°,
故答案为:119.
12.(3分)某数学兴趣小组的同学们,把6个形状、大小完全相同的长方形叠加成如图所示的三个上升的“L”图案,放入平面直角坐标系中,若点A的坐标为(﹣2,7),则点B的坐标为 (﹣5,5) .
【解答】解:设长方形的长为x,宽为y,
根据题意得,,
解得,
∴点B的坐标为(﹣5,5),
故答案为:(﹣5,5).
13.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D为边AC上一动点,DE⊥AB交AB于点E,将∠A沿直线DE折叠,点A的对应点为F,当△DFC是直角三角形时,AD的长为 或 .
【解答】解:当∠DFC=90°时,
∵将∠A沿直线DE折叠,点A的对应点为F.
∴∠A=∠AFD,AD=DF,
∵∠ACB=90°,∠DFC=90°,
∴∠A+∠B=90°,∠AFD+∠BFC=90°,
∴∠BFC=∠B,
∴FC=BC=6,
在Rt△DFC中,CD2=DF2+CF2.
∴(8﹣AD)2=AD2+36,
∴AD,
当点F与点B重合时,AD=DF,
∵DF2=BC2+CD2,
∴AD2=(8﹣AD)2+36,
∴AD,
故答案为:或.
三、解答题:(本大题共7题;其中14题6分,15题8分,16题8分,17题9分,18题10分,19题10分,20题10分,共61分)
14.(6分)化简:.
【解答】解:
=1+2(﹣2)
.
15.(8分)解方程组:
(1);
(2).
【解答】解:(1),
②﹣①×2得:x=2,
将x=2代入①得:2﹣2y=2,
解得:y=0,
故原方程组的解为;
(2)原方程整理得,
①+②得:x﹣y=2③,
①﹣②得:x+y=10④,
③+④得:2x=12,
解得:x=6,
将x=6代入②得:6﹣y=2,
解得:y=4,
故原方程组的解为.
16.(8分)如图,在平面直角坐标系中△ABC如图所示.
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1.
(2)①分别写出△A1B1C1各顶点坐标.
②求△A1B1C1的面积.
(3)若以B点为圆心,AB的长为半径作弧线,交射线BB1于点E,请在图中作出线段BE(留下作图痕迹),并求出E点的坐标.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)①由图可得,A1(﹣5,﹣1),B1(﹣2,﹣5),C1(﹣6,﹣4).
②△A1B1C1的面积为.
(3)如图,线段BE即为所求.
由勾股定理得,AB5,
∴BE=AB=5,
∵点E在射线BB1上,
∴点E的坐标为(﹣3,﹣5).
17.(9分)近年来,新能源汽车扎根坪山、立足深圳、放眼全球,通过一路自主创新,发展加速狂飙.坪山区作为深圳打造“新一代世界一流汽车城”的核心承载区,新能源汽车消费市场有巨大的发展潜力,因此坪山区居民对电车充电桩的需求也在不断增加,目前公共充电桩的收费方式有:按电量计费、按时间计费、按峰谷计费,为了解调整充电桩收费方式的社会反响,新能源汽车工厂相关负责人随机访问了坪山区的部分车主,就“每月每部车的用电量”和“认为公共充电桩该如何收费”两个问题进行调查,并把调查结果整理成下面的图1,图2.(其中图1每月每部车用电范围为150~450千瓦时)
收费方式 收费标准
按电量计费 1.2元/千瓦时
按时间计费 2元/小时
按峰谷计费 10:00﹣19:00(低峰期,0.9元/千瓦时) 19:00﹣次日10:00(高峰期,1.5元/千瓦时)
在所有受调查的车主中共有1050位车主认为充电桩应该“按电量计费”,根据负责人绘制的图表和发现的信息,完成下列问题:
(1)n= 210 ,负责人共调查了 1800 位车主,并补全图1;
(2)如果坪山区有96000位车主,请你估计坪山区内认为充电桩收费应该“按峰谷计费”的车主数有多少?
(3)据了解深深的爸爸居住在坪山区,每天需要开电车往返于公司上班,已知他每个月电车耗电量范围落在图1的中位数 250~300 千瓦时,且他一般是在每天的12:00﹣20:00充电,如果你是深深的爸爸,结合以上信息,请分别从两个角度考虑:该选哪种计费方式的充电桩给电车充电?并说明理由(理由充分即可).
【解答】解:(1)n=360﹣120﹣30=210,
(位),
1800﹣260﹣330﹣290﹣280﹣160=480,
故答案为:210;1800;
(2)(位),
答:坪山区内认为充电桩收费应该“按峰谷计费”的车主数有8000位;
(3)∵260+330=590(位),260+330+480=1070(位),
∴中位数为250~300千瓦时,
故答案为:250~300;
应该选择“按峰谷计费”,理由如下:
①每月耗电量不大,选择“按时间计费”不划算;
②可在每天12:00﹣19:00低峰期充电,比“按电量计费”更划算.
18.(10分)【教材呈现】
将正方形的四个顶点用线段连接,什么样的连法最短?研究发现,并非对角线最短,而是如图所示的连法最短(即用线段AE、DE、EF、BF、CF把四个顶点连接起来).已知如图1:∠DAE=∠ADE=30°,∠AEF=∠BFE=120°.
(1)由图1可知,线段AB和EF的位置关系为: AB∥EF ;
【问题探究】
(2)某数学兴趣小组发现,图1所示图形 是 (是/不是)轴对称图形,于是他们如图2构造了△AF′D≌△BFC,发现△AF′E是 等边 三角形,请结合以上结论,猜想线段AE与OE的数量关系,并证明.
【问题解决】
(3)在第(2)问的基础上,若AB=6,求最短连法的线段和,即AE+DE+EF+BF+CF的值.
【解答】解:(1)∵四边形ABCD是正方形,
∴∠BAD=90°,
∵∠DAE=30°,
∴∠BAE=60°,
∵∠AEF=120°,
∴∠BAE+∠AEF=180°,
∴AB∥EF,
故答案为:AB∥EF;
(2)图1所示图形是轴对称图形,如图2构造了△AF′D≌△BFC,发现△AF′E是等边三角形,
猜想线段AE=2OE,证明如下:
由(1)AB∥EF,
∵∠BFE=120°,
∴∠ABF=60°,
∴∠FBC=30°,
同理∠FCB=30°,
∴△AED≌△BFC(ASA),
∵△AF′D≌△BFC,
∴△AF′D≌△AED,
∴AF′=AE,∠F′AE=60°,
∴△AF′E是等边三角形,
∵∠F′AD=∠EAD=30°,
∴AO⊥EF′,OF′=OE,
∴AE=2OE,
故答案为:是,等边;
(3)∵△AF′E是等边三角形,
同(2)可知:△DF′E是等边三角形,
∴AE=DE=EF′,
由(1)知:AO⊥EF′,
∴AO=DOADAB=3,
∴OE=3,
∴AE=2OE=2,
∴EF=AB﹣2OE=6﹣AE,
∴AE+DE+EF+BF+CF
=4AE+6﹣AE,
=3AE+6
=66
∴AE+DE+EF+BF+CF的值为66.
19.(10分)请根据以下素材,完成探究任务.
关于出票问题的探究
素材1 为提升市民审美品味和高雅文化消费,位于坪山文化聚落的坪山大剧院,每月都会在综合剧场(可容纳1200名观众)上演高品质的若干场剧目.按文化和旅游部的相关规定,剧院等演出场所的上座率(100%)原则上不得超过75%.
素材2 “每月一剧”惠民计划:为进一步提升辖区居民的幸福感,丰富居民群众的精神文化生活,坪山街道新和社区通过民生微实事项目平台,联合坪山大剧院联手推出惠民观剧活动,辖区居民只需40元即可购买一张当月上演的一场剧目前往观剧,数量有限,先购先得!
素材3 2024年11月的一场话剧推出A、B两种观赏票价,并参与“每月一剧”惠民购票活动.已知A种票10张、B种票5张、惠民票5张,共需3900元;购买2张B种票比购买1张A种票多出的费用,可购得惠民票2张.
问题解决
任务1 据悉,该话剧深受广大市民欢迎,上座人数恰好达到相关规定的上限,则观剧人数有 900 人.
任务2 设该话剧A种票价a元,B种票价b元,求出该话剧的A种、B种票价.
任务3 若A种票的持票人数y与B种票的持票人数x满足如图所示函数图象(其中x取正整数).请写出该场话剧票务收入W与x的函数表达式,求出该场话剧的最大票务收入.
【解答】解:任务1:设观剧人数为x人,则100%≤75%,
解得:x≤900,
∴x的最大值为:900,
故答案为:900;
任务2:由题意得:,
解得:,
答:该话剧的A种票价为280元、B种票价为180元;
任务3:设y=kx+b,
则,
解得:,
∴y=﹣2x+1000,
∴w=280y+180x+40×(900﹣x﹣y)=280(﹣2x+1000)+180x+40(900﹣x+2x﹣1000)=﹣340x+276000,
∵﹣340<0,
∴w随x的增大而减小,
∵300≤x≤500,
∴当x=300时,w取最大值,为﹣340×300+276000=174000(元),
答:该场话剧的最大票务收入174000元.
20.(10分)折纸是一种以纸张折成各种不同形状的艺术活动,它是中国非物质文化遗产之一,具有悠久的历史和丰富的文化内涵.在现代,折纸艺术得到了进一步的发展和创新,材料已不只限于使用纸张,而且它还与自然科学结合在一起,发展出了折纸几何学,成为现代几何学的一个分支,形成有趣的“折纸数学”.
某校八年级一数学学习兴趣小组准备参加区数学创新能力大赛,他们尝试用一张直角三角形纸片探究折纸中的几何问题.
如图,他们准备了一张直角三角形纸片,记为Rt△ABC,∠C=90°,BC=3,AC=4.点P在线段AC上,将△ABP沿着直线BP翻折,点A落在点D处,BD交AC于点E.
【操作一】
如图1,小组成员甲将纸片折叠,使AP⊥DP,观察发现△BCP的形状是 等腰直角三角形 ,此时AP为 1 ;
【操作二】
如图2,小组成员乙将纸片折叠,使AB与CB重叠,观察图形,请帮他求出△ADP的面积;
【操作三】
如图3,小组成员丙在图2的基础上,尝试在线段BC和AB上添加两个动点M、N,连接PM、MN,你能判断在M、N的运动过程中PM+MN是否存在最小值吗?如存在请求出PM+MN的最小值.
【解答】解:【操作一】
由折叠得,
∠APB=∠BPD,
∵PD⊥DP,
∴∠CPD=90°,
设∠CPB=α,则∠BPD=∠APB=180°﹣α,
由∠BPD﹣∠CPB=∠CPD得,
(180°﹣α)﹣α=90°,
∴α=45°,
∴∠CPB=45°
∵∠C=90°,
∴∠CBP=∠CPB=45°,
∴PC=BC=3,
∴△BCP是等腰直角三角形,AP=AC﹣PC=1,
故答案为:等腰直角三角形,1;
【操作二】
∵∠ACB=90°,BC=3,AC=4,
∴AB=5,
由折叠得,
BD=AB=5,DP=AP,
∴CD=BD﹣BC=2,
设DP=AP=x,则CP=4﹣x,
在Rt△DCP中,由勾股定理得,
CD2+CP2=DP2,
∴22+(4﹣x)2=x2,
∴x,
∴AP,
∴S△ADP;
【操作三】
如图,
PM+MN存在最小值,
作点P关于BC的对称点Q,作QN⊥AB于N,交BC于M,则PM+MN最小=QN,
∴CQ=CP,
由上知:CP=4﹣x=4,
∴CQ,
∴,
连接BQ,
由S△ABQ得,
5,
∴QN.
第1页(共1页)
一、选择题:(本大题8个小题,每小题3分,共24分)
1.(3分)f(x)=ex是一个数学函数,它表示自然数e的指数次幂.其中自然数e是一个无理数(e=2.718281828459045 )则在下列实数中,( )也是无理数
A. B. C.3.14 D.
2.(3分)下列计算中,正确的是( )
A. B. C. D.
3.(3分)若a,b,c是三角形的三边长,则满足下列条件的a,b,c不能构成直角三角形的是( )
A.a=1,b=1,c=2 B.a=b=5,c=5
C.a:b:c=3:4:5 D.a=5,b=13,c=12
4.(3分)函数y=﹣2x+1的图象一定经过下列四个点中的( )
A.(1,﹣3) B.(﹣2,4) C.(﹣1,1) D.(0,1)
5.(3分)科技是第一生产力,创新是第一动力,教育、科技、人才是全面建设社会主义现代化国家的基础性、战略性支撑.某校准备从甲、乙、丙、丁四个科技小组中选出一组,参加坪山区中小学科技创新竞赛,如表记录了各组平时成绩的平均数(单位:分)及方差.若要选出一个成绩好且状态稳定的小组去参加比赛,则应选择的小组是( )
甲 乙 丙 丁
平均数 93 97 97 95
方差 0.8 0.8 1.2 1.2
A.甲 B.乙 C.丙 D.丁
6.(3分)某粮食生产专业户去年计划生产水稻和小麦共18t,实际生产了20t,其中水稻超产15%,小麦超产10%,问:该专业户去年计划生产水稻、小麦各多少吨?设该专业户去年计划生产水稻x吨,小麦y吨,则下列方程组正确的是( )
A.
B.
C.
D.
7.(3分)如图,在△ABC中,∠B=56°,∠C=37°,AD和AE分别是△ABC的高和角平分线,则∠DAE的度数为( )
A.7.5° B.8.5° C.9.5° D.10.5°
8.(3分)已知直线l1:y=kx+b与直线都经过,直线l1交x轴于点A,交y轴于点B(0,4),直线l2交y轴于点C,交x轴于点D.直线l3∥直线l1且经过原点,且与直线l2交于点F,点P为x轴上任意一点,连接PC、PF.对于以下结论,错误的是( )
A.方程组的解为
B.S△OFD=3
C.△AED为直角三角形
D.当PF+PC的值最小时,点P的坐标为
二、填空题:(本大题5个小题,每小题3分,共15分)
9.(3分)8的立方根是 .
10.(3分)在坪山区某校文学节演讲比赛中,甲的演讲内容、演讲能力、演讲效果成绩如表所示:
项目 演讲内容 演讲能力 演讲效果
成绩/分 80 90 80
若按照演讲内容占60%,演讲能力占20%,演讲效果占20%,计算选手的综合成绩,则该选手的综合成绩为 分.
11.(3分)如图,△ABC中,∠ABC和∠ACB的角平分线BE与CF相交于点O,∠A=58°,则∠BOC为 °.
12.(3分)某数学兴趣小组的同学们,把6个形状、大小完全相同的长方形叠加成如图所示的三个上升的“L”图案,放入平面直角坐标系中,若点A的坐标为(﹣2,7),则点B的坐标为 .
13.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D为边AC上一动点,DE⊥AB交AB于点E,将∠A沿直线DE折叠,点A的对应点为F,当△DFC是直角三角形时,AD的长为 .
三、解答题:(本大题共7题;其中14题6分,15题8分,16题8分,17题9分,18题10分,19题10分,20题10分,共61分)
14.(6分)化简:.
15.(8分)解方程组:
(1);
(2).
16.(8分)如图,在平面直角坐标系中△ABC如图所示.
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1.
(2)①分别写出△A1B1C1各顶点坐标.
②求△A1B1C1的面积.
(3)若以B点为圆心,AB的长为半径作弧线,交射线BB1于点E,请在图中作出线段BE(留下作图痕迹),并求出E点的坐标.
17.(9分)近年来,新能源汽车扎根坪山、立足深圳、放眼全球,通过一路自主创新,发展加速狂飙.坪山区作为深圳打造“新一代世界一流汽车城”的核心承载区,新能源汽车消费市场有巨大的发展潜力,因此坪山区居民对电车充电桩的需求也在不断增加,目前公共充电桩的收费方式有:按电量计费、按时间计费、按峰谷计费,为了解调整充电桩收费方式的社会反响,新能源汽车工厂相关负责人随机访问了坪山区的部分车主,就“每月每部车的用电量”和“认为公共充电桩该如何收费”两个问题进行调查,并把调查结果整理成下面的图1,图2.(其中图1每月每部车用电范围为150~450千瓦时)
收费方式 收费标准
按电量计费 1.2元/千瓦时
按时间计费 2元/小时
按峰谷计费 10:00﹣19:00(低峰期,0.9元/千瓦时) 19:00﹣次日10:00(高峰期,1.5元/千瓦时)
在所有受调查的车主中共有1050位车主认为充电桩应该“按电量计费”,根据负责人绘制的图表和发现的信息,完成下列问题:
(1)n= ,负责人共调查了 位车主,并补全图1;
(2)如果坪山区有96000位车主,请你估计坪山区内认为充电桩收费应该“按峰谷计费”的车主数有多少?
(3)据了解深深的爸爸居住在坪山区,每天需要开电车往返于公司上班,已知他每个月电车耗电量范围落在图1的中位数 千瓦时,且他一般是在每天的12:00﹣20:00充电,如果你是深深的爸爸,结合以上信息,请分别从两个角度考虑:该选哪种计费方式的充电桩给电车充电?并说明理由(理由充分即可).
18.(10分)【教材呈现】
将正方形的四个顶点用线段连接,什么样的连法最短?研究发现,并非对角线最短,而是如图所示的连法最短(即用线段AE、DE、EF、BF、CF把四个顶点连接起来).已知如图1:∠DAE=∠ADE=30°,∠AEF=∠BFE=120°.
(1)由图1可知,线段AB和EF的位置关系为: ;
【问题探究】
(2)某数学兴趣小组发现,图1所示图形 (是/不是)轴对称图形,于是他们如图2构造了△AF′D≌△BFC,发现△AF′E是 三角形,请结合以上结论,猜想线段AE与OE的数量关系,并证明.
【问题解决】
(3)在第(2)问的基础上,若AB=6,求最短连法的线段和,即AE+DE+EF+BF+CF的值.
19.(10分)请根据以下素材,完成探究任务.
关于出票问题的探究
素材1 为提升市民审美品味和高雅文化消费,位于坪山文化聚落的坪山大剧院,每月都会在综合剧场(可容纳1200名观众)上演高品质的若干场剧目.按文化和旅游部的相关规定,剧院等演出场所的上座率(100%)原则上不得超过75%.
素材2 “每月一剧”惠民计划:为进一步提升辖区居民的幸福感,丰富居民群众的精神文化生活,坪山街道新和社区通过民生微实事项目平台,联合坪山大剧院联手推出惠民观剧活动,辖区居民只需40元即可购买一张当月上演的一场剧目前往观剧,数量有限,先购先得!
素材3 2024年11月的一场话剧推出A、B两种观赏票价,并参与“每月一剧”惠民购票活动.已知A种票10张、B种票5张、惠民票5张,共需3900元;购买2张B种票比购买1张A种票多出的费用,可购得惠民票2张.
问题解决
任务1 据悉,该话剧深受广大市民欢迎,上座人数恰好达到相关规定的上限,则观剧人数有 人.
任务2 设该话剧A种票价a元,B种票价b元,求出该话剧的A种、B种票价.
任务3 若A种票的持票人数y与B种票的持票人数x满足如图所示函数图象(其中x取正整数).请写出该场话剧票务收入W与x的函数表达式,求出该场话剧的最大票务收入.
20.(10分)折纸是一种以纸张折成各种不同形状的艺术活动,它是中国非物质文化遗产之一,具有悠久的历史和丰富的文化内涵.在现代,折纸艺术得到了进一步的发展和创新,材料已不只限于使用纸张,而且它还与自然科学结合在一起,发展出了折纸几何学,成为现代几何学的一个分支,形成有趣的“折纸数学”.
某校八年级一数学学习兴趣小组准备参加区数学创新能力大赛,他们尝试用一张直角三角形纸片探究折纸中的几何问题.
如图,他们准备了一张直角三角形纸片,记为Rt△ABC,∠C=90°,BC=3,AC=4.点P在线段AC上,将△ABP沿着直线BP翻折,点A落在点D处,BD交AC于点E.
【操作一】
如图1,小组成员甲将纸片折叠,使AP⊥DP,观察发现△BCP的形状是 ,此时AP为 ;
【操作二】
如图2,小组成员乙将纸片折叠,使AB与CB重叠,观察图形,请帮他求出△ADP的面积;
【操作三】
如图3,小组成员丙在图2的基础上,尝试在线段BC和AB上添加两个动点M、N,连接PM、MN,你能判断在M、N的运动过程中PM+MN是否存在最小值吗?如存在请求出PM+MN的最小值.
2024-2025学年广东省深圳市坪山区八年级(上)期末数学试卷
参考答案与试题解析
题号 1 2 3 4 5 6 7 8
答案 D C A D B A C B
一、选择题:(本大题8个小题,每小题3分,共24分)
1.(3分)f(x)=ex是一个数学函数,它表示自然数e的指数次幂.其中自然数e是一个无理数(e=2.718281828459045 )则在下列实数中,( )也是无理数
A. B. C.3.14 D.
【解答】解:根据无理数的定义可得,是无理数.
故选:D.
2.(3分)下列计算中,正确的是( )
A. B. C. D.
【解答】解:与不是同类项,不能进一步计算,
故A选项不正确,不符合题意;
4与不是同类项,不能进一步计算,
故B选项不正确,不符合题意;
,
故C选项正确,符合题意;
与3不是同类项,不能进一步计算,
故D选项不正确,不符合题意.
故选:C.
3.(3分)若a,b,c是三角形的三边长,则满足下列条件的a,b,c不能构成直角三角形的是( )
A.a=1,b=1,c=2 B.a=b=5,c=5
C.a:b:c=3:4:5 D.a=5,b=13,c=12
【解答】解:A、1+1=2,12+12≠22,不能构成直角三角形,符合题意;
B、52+52=(5)2,能构成直角三角形,不符合题意;
C、设a=3x,则b=4x,c=5x,
(3x)2+(4x)2=(5x)2,即a2+b2=c2,能构成直角三角形,不符合题意;
D、52+122=132,能构成直角三角形,不符合题意,
故选:A.
4.(3分)函数y=﹣2x+1的图象一定经过下列四个点中的( )
A.(1,﹣3) B.(﹣2,4) C.(﹣1,1) D.(0,1)
【解答】解:A、当x=1时,y=﹣1,故函数y=﹣2x+1的图象不经过(1,﹣3),不符合题意;
B、当x=﹣2时,y=5,故函数y=﹣2x+1的图象不经过(﹣2,4),不符合题意;
C、当x=﹣1时,y=3,故函数y=﹣2x+1的图象不经过(﹣1,1),不符合题意;
D、当x=0时,y=1,故函数y=﹣2x+1的图象经过(0,1),符合题意;
故选:D.
5.(3分)科技是第一生产力,创新是第一动力,教育、科技、人才是全面建设社会主义现代化国家的基础性、战略性支撑.某校准备从甲、乙、丙、丁四个科技小组中选出一组,参加坪山区中小学科技创新竞赛,如表记录了各组平时成绩的平均数(单位:分)及方差.若要选出一个成绩好且状态稳定的小组去参加比赛,则应选择的小组是( )
甲 乙 丙 丁
平均数 93 97 97 95
方差 0.8 0.8 1.2 1.2
A.甲 B.乙 C.丙 D.丁
【解答】解:∵乙的平均数最大,方差最小,
∴乙成绩好且状态稳定,
故选:B.
6.(3分)某粮食生产专业户去年计划生产水稻和小麦共18t,实际生产了20t,其中水稻超产15%,小麦超产10%,问:该专业户去年计划生产水稻、小麦各多少吨?设该专业户去年计划生产水稻x吨,小麦y吨,则下列方程组正确的是( )
A.
B.
C.
D.
【解答】解:由题意得,.
故选:A.
7.(3分)如图,在△ABC中,∠B=56°,∠C=37°,AD和AE分别是△ABC的高和角平分线,则∠DAE的度数为( )
A.7.5° B.8.5° C.9.5° D.10.5°
【解答】解:在△ABC中,∠B=56°,∠C=37°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣56°﹣37°=87°,
∵AE是△ABC的角平分线,
∴∠BAE43.5°,
∵AD是△ABC的高,
∴∠ADB=90°,
∵∠B=56°,
∴∠BAD=90°﹣∠B=90°﹣56°=34°,
∴∠DAE=∠BAE﹣∠BAD=43.5°﹣34°=9.5°,
故选:C.
8.(3分)已知直线l1:y=kx+b与直线都经过,直线l1交x轴于点A,交y轴于点B(0,4),直线l2交y轴于点C,交x轴于点D.直线l3∥直线l1且经过原点,且与直线l2交于点F,点P为x轴上任意一点,连接PC、PF.对于以下结论,错误的是( )
A.方程组的解为
B.S△OFD=3
C.△AED为直角三角形
D.当PF+PC的值最小时,点P的坐标为
【解答】解:A、∵直线l1:y=kx+b与直线都经过,
∴方程组的解为,故不符合题意;
B、把,点B(0,4)代入y=kx+b得,
∴,
∴直线l1:y=2x+4,
∵直线l3∥直线l1且经过原点,
∴直线l3的解析式为y=2x,
把代入yx+m得,m,
∴m=2,
∴直线l2:y,
解得,
∴F(,),
在y中,令y=0,则x+2=0,
解得x=4,
∴D(4,0),
∴S△OFD,故符合题意;
C、在y=2x+4中,令y=0,则2x+4=0,
∴x=﹣2,
∴A(﹣2,0),
∴AE2=(﹣2)2,DE2=(4)2,AD2=(﹣2﹣4)2=36,
∴AE2+DE2=AD2,
∴∠AED=90°,
∴△AED为直角三角形;不符合题意;
D、∵直线l2交y轴于点C,
∴C(0,2),
作点C故x轴的对称点C′,连接C′F交x轴于P,
此时,PF+PC的值最小,
设直线C′P的解析式为y=mx+n,
∵C′(0,﹣2),
∴,
∴
∴直线C′P的解析式为yx﹣2,
当y=0时,x,
∴P(,0),不符合题意;
故选:B.
二、填空题:(本大题5个小题,每小题3分,共15分)
9.(3分)8的立方根是 2 .
【解答】解:∵23=8,
∴8的立方根是2.
故答案为:2.
10.(3分)在坪山区某校文学节演讲比赛中,甲的演讲内容、演讲能力、演讲效果成绩如表所示:
项目 演讲内容 演讲能力 演讲效果
成绩/分 80 90 80
若按照演讲内容占60%,演讲能力占20%,演讲效果占20%,计算选手的综合成绩,则该选手的综合成绩为 82 分.
【解答】解:该选手的综合成绩为:80×60%+90×20%+80×20%=82(分),
故答案为:82.
11.(3分)如图,△ABC中,∠ABC和∠ACB的角平分线BE与CF相交于点O,∠A=58°,则∠BOC为 119 °.
【解答】解:在△ABC中,∠A=58°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣58°=122°,
∵∠ABC和∠ACB的角平分线BE与CF相交于点O,
∴∠OBC,∠OCBACB,
∴∠OBC+∠OCB122°=61°,
在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣61°=119°,
故答案为:119.
12.(3分)某数学兴趣小组的同学们,把6个形状、大小完全相同的长方形叠加成如图所示的三个上升的“L”图案,放入平面直角坐标系中,若点A的坐标为(﹣2,7),则点B的坐标为 (﹣5,5) .
【解答】解:设长方形的长为x,宽为y,
根据题意得,,
解得,
∴点B的坐标为(﹣5,5),
故答案为:(﹣5,5).
13.(3分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D为边AC上一动点,DE⊥AB交AB于点E,将∠A沿直线DE折叠,点A的对应点为F,当△DFC是直角三角形时,AD的长为 或 .
【解答】解:当∠DFC=90°时,
∵将∠A沿直线DE折叠,点A的对应点为F.
∴∠A=∠AFD,AD=DF,
∵∠ACB=90°,∠DFC=90°,
∴∠A+∠B=90°,∠AFD+∠BFC=90°,
∴∠BFC=∠B,
∴FC=BC=6,
在Rt△DFC中,CD2=DF2+CF2.
∴(8﹣AD)2=AD2+36,
∴AD,
当点F与点B重合时,AD=DF,
∵DF2=BC2+CD2,
∴AD2=(8﹣AD)2+36,
∴AD,
故答案为:或.
三、解答题:(本大题共7题;其中14题6分,15题8分,16题8分,17题9分,18题10分,19题10分,20题10分,共61分)
14.(6分)化简:.
【解答】解:
=1+2(﹣2)
.
15.(8分)解方程组:
(1);
(2).
【解答】解:(1),
②﹣①×2得:x=2,
将x=2代入①得:2﹣2y=2,
解得:y=0,
故原方程组的解为;
(2)原方程整理得,
①+②得:x﹣y=2③,
①﹣②得:x+y=10④,
③+④得:2x=12,
解得:x=6,
将x=6代入②得:6﹣y=2,
解得:y=4,
故原方程组的解为.
16.(8分)如图,在平面直角坐标系中△ABC如图所示.
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1.
(2)①分别写出△A1B1C1各顶点坐标.
②求△A1B1C1的面积.
(3)若以B点为圆心,AB的长为半径作弧线,交射线BB1于点E,请在图中作出线段BE(留下作图痕迹),并求出E点的坐标.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)①由图可得,A1(﹣5,﹣1),B1(﹣2,﹣5),C1(﹣6,﹣4).
②△A1B1C1的面积为.
(3)如图,线段BE即为所求.
由勾股定理得,AB5,
∴BE=AB=5,
∵点E在射线BB1上,
∴点E的坐标为(﹣3,﹣5).
17.(9分)近年来,新能源汽车扎根坪山、立足深圳、放眼全球,通过一路自主创新,发展加速狂飙.坪山区作为深圳打造“新一代世界一流汽车城”的核心承载区,新能源汽车消费市场有巨大的发展潜力,因此坪山区居民对电车充电桩的需求也在不断增加,目前公共充电桩的收费方式有:按电量计费、按时间计费、按峰谷计费,为了解调整充电桩收费方式的社会反响,新能源汽车工厂相关负责人随机访问了坪山区的部分车主,就“每月每部车的用电量”和“认为公共充电桩该如何收费”两个问题进行调查,并把调查结果整理成下面的图1,图2.(其中图1每月每部车用电范围为150~450千瓦时)
收费方式 收费标准
按电量计费 1.2元/千瓦时
按时间计费 2元/小时
按峰谷计费 10:00﹣19:00(低峰期,0.9元/千瓦时) 19:00﹣次日10:00(高峰期,1.5元/千瓦时)
在所有受调查的车主中共有1050位车主认为充电桩应该“按电量计费”,根据负责人绘制的图表和发现的信息,完成下列问题:
(1)n= 210 ,负责人共调查了 1800 位车主,并补全图1;
(2)如果坪山区有96000位车主,请你估计坪山区内认为充电桩收费应该“按峰谷计费”的车主数有多少?
(3)据了解深深的爸爸居住在坪山区,每天需要开电车往返于公司上班,已知他每个月电车耗电量范围落在图1的中位数 250~300 千瓦时,且他一般是在每天的12:00﹣20:00充电,如果你是深深的爸爸,结合以上信息,请分别从两个角度考虑:该选哪种计费方式的充电桩给电车充电?并说明理由(理由充分即可).
【解答】解:(1)n=360﹣120﹣30=210,
(位),
1800﹣260﹣330﹣290﹣280﹣160=480,
故答案为:210;1800;
(2)(位),
答:坪山区内认为充电桩收费应该“按峰谷计费”的车主数有8000位;
(3)∵260+330=590(位),260+330+480=1070(位),
∴中位数为250~300千瓦时,
故答案为:250~300;
应该选择“按峰谷计费”,理由如下:
①每月耗电量不大,选择“按时间计费”不划算;
②可在每天12:00﹣19:00低峰期充电,比“按电量计费”更划算.
18.(10分)【教材呈现】
将正方形的四个顶点用线段连接,什么样的连法最短?研究发现,并非对角线最短,而是如图所示的连法最短(即用线段AE、DE、EF、BF、CF把四个顶点连接起来).已知如图1:∠DAE=∠ADE=30°,∠AEF=∠BFE=120°.
(1)由图1可知,线段AB和EF的位置关系为: AB∥EF ;
【问题探究】
(2)某数学兴趣小组发现,图1所示图形 是 (是/不是)轴对称图形,于是他们如图2构造了△AF′D≌△BFC,发现△AF′E是 等边 三角形,请结合以上结论,猜想线段AE与OE的数量关系,并证明.
【问题解决】
(3)在第(2)问的基础上,若AB=6,求最短连法的线段和,即AE+DE+EF+BF+CF的值.
【解答】解:(1)∵四边形ABCD是正方形,
∴∠BAD=90°,
∵∠DAE=30°,
∴∠BAE=60°,
∵∠AEF=120°,
∴∠BAE+∠AEF=180°,
∴AB∥EF,
故答案为:AB∥EF;
(2)图1所示图形是轴对称图形,如图2构造了△AF′D≌△BFC,发现△AF′E是等边三角形,
猜想线段AE=2OE,证明如下:
由(1)AB∥EF,
∵∠BFE=120°,
∴∠ABF=60°,
∴∠FBC=30°,
同理∠FCB=30°,
∴△AED≌△BFC(ASA),
∵△AF′D≌△BFC,
∴△AF′D≌△AED,
∴AF′=AE,∠F′AE=60°,
∴△AF′E是等边三角形,
∵∠F′AD=∠EAD=30°,
∴AO⊥EF′,OF′=OE,
∴AE=2OE,
故答案为:是,等边;
(3)∵△AF′E是等边三角形,
同(2)可知:△DF′E是等边三角形,
∴AE=DE=EF′,
由(1)知:AO⊥EF′,
∴AO=DOADAB=3,
∴OE=3,
∴AE=2OE=2,
∴EF=AB﹣2OE=6﹣AE,
∴AE+DE+EF+BF+CF
=4AE+6﹣AE,
=3AE+6
=66
∴AE+DE+EF+BF+CF的值为66.
19.(10分)请根据以下素材,完成探究任务.
关于出票问题的探究
素材1 为提升市民审美品味和高雅文化消费,位于坪山文化聚落的坪山大剧院,每月都会在综合剧场(可容纳1200名观众)上演高品质的若干场剧目.按文化和旅游部的相关规定,剧院等演出场所的上座率(100%)原则上不得超过75%.
素材2 “每月一剧”惠民计划:为进一步提升辖区居民的幸福感,丰富居民群众的精神文化生活,坪山街道新和社区通过民生微实事项目平台,联合坪山大剧院联手推出惠民观剧活动,辖区居民只需40元即可购买一张当月上演的一场剧目前往观剧,数量有限,先购先得!
素材3 2024年11月的一场话剧推出A、B两种观赏票价,并参与“每月一剧”惠民购票活动.已知A种票10张、B种票5张、惠民票5张,共需3900元;购买2张B种票比购买1张A种票多出的费用,可购得惠民票2张.
问题解决
任务1 据悉,该话剧深受广大市民欢迎,上座人数恰好达到相关规定的上限,则观剧人数有 900 人.
任务2 设该话剧A种票价a元,B种票价b元,求出该话剧的A种、B种票价.
任务3 若A种票的持票人数y与B种票的持票人数x满足如图所示函数图象(其中x取正整数).请写出该场话剧票务收入W与x的函数表达式,求出该场话剧的最大票务收入.
【解答】解:任务1:设观剧人数为x人,则100%≤75%,
解得:x≤900,
∴x的最大值为:900,
故答案为:900;
任务2:由题意得:,
解得:,
答:该话剧的A种票价为280元、B种票价为180元;
任务3:设y=kx+b,
则,
解得:,
∴y=﹣2x+1000,
∴w=280y+180x+40×(900﹣x﹣y)=280(﹣2x+1000)+180x+40(900﹣x+2x﹣1000)=﹣340x+276000,
∵﹣340<0,
∴w随x的增大而减小,
∵300≤x≤500,
∴当x=300时,w取最大值,为﹣340×300+276000=174000(元),
答:该场话剧的最大票务收入174000元.
20.(10分)折纸是一种以纸张折成各种不同形状的艺术活动,它是中国非物质文化遗产之一,具有悠久的历史和丰富的文化内涵.在现代,折纸艺术得到了进一步的发展和创新,材料已不只限于使用纸张,而且它还与自然科学结合在一起,发展出了折纸几何学,成为现代几何学的一个分支,形成有趣的“折纸数学”.
某校八年级一数学学习兴趣小组准备参加区数学创新能力大赛,他们尝试用一张直角三角形纸片探究折纸中的几何问题.
如图,他们准备了一张直角三角形纸片,记为Rt△ABC,∠C=90°,BC=3,AC=4.点P在线段AC上,将△ABP沿着直线BP翻折,点A落在点D处,BD交AC于点E.
【操作一】
如图1,小组成员甲将纸片折叠,使AP⊥DP,观察发现△BCP的形状是 等腰直角三角形 ,此时AP为 1 ;
【操作二】
如图2,小组成员乙将纸片折叠,使AB与CB重叠,观察图形,请帮他求出△ADP的面积;
【操作三】
如图3,小组成员丙在图2的基础上,尝试在线段BC和AB上添加两个动点M、N,连接PM、MN,你能判断在M、N的运动过程中PM+MN是否存在最小值吗?如存在请求出PM+MN的最小值.
【解答】解:【操作一】
由折叠得,
∠APB=∠BPD,
∵PD⊥DP,
∴∠CPD=90°,
设∠CPB=α,则∠BPD=∠APB=180°﹣α,
由∠BPD﹣∠CPB=∠CPD得,
(180°﹣α)﹣α=90°,
∴α=45°,
∴∠CPB=45°
∵∠C=90°,
∴∠CBP=∠CPB=45°,
∴PC=BC=3,
∴△BCP是等腰直角三角形,AP=AC﹣PC=1,
故答案为:等腰直角三角形,1;
【操作二】
∵∠ACB=90°,BC=3,AC=4,
∴AB=5,
由折叠得,
BD=AB=5,DP=AP,
∴CD=BD﹣BC=2,
设DP=AP=x,则CP=4﹣x,
在Rt△DCP中,由勾股定理得,
CD2+CP2=DP2,
∴22+(4﹣x)2=x2,
∴x,
∴AP,
∴S△ADP;
【操作三】
如图,
PM+MN存在最小值,
作点P关于BC的对称点Q,作QN⊥AB于N,交BC于M,则PM+MN最小=QN,
∴CQ=CP,
由上知:CP=4﹣x=4,
∴CQ,
∴,
连接BQ,
由S△ABQ得,
5,
∴QN.
第1页(共1页)
同课章节目录
