数学:1.1《关于“球”的常见问题》教案(新人教a版必修2)
文档属性
| 名称 | 数学:1.1《关于“球”的常见问题》教案(新人教a版必修2) |  | |
| 格式 | rar | ||
| 文件大小 | 53.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-03 14:11:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
【关于“球”的常见问题】
常见问题1: 问题:怎样把圆和球的主要性质进行对照?
解答:
答:
圆的主要性质 球的主要性质
1 平面内与定点距离等于定长的点集(轨迹) 空间与定点距离等于定长的点集(轨迹)
2 同圆(或等圆)的半径相等,直径是半径的2倍 同球(或等球)的半径相等,直径是半径的2倍
3 与弦垂直的直径过弦的中点,圆半径2=圆心到弦距离2+弦长的一半2 与截面积垂直的直径过截面圆的圆心,球半径2=球心到截面圆距离2+截面圆的半径2
4 不过圆心的弦小于直径;经过圆心的弦是直径,是最大的弦 不过球心的截得的是球的小圆,其半径和面积都小于球的大圆的半径和面积;经过球心的截面截得的是球的大圆,是最大的截面圆
5 过切点的圆半径垂直于圆的切线 过切点的球半径垂直于球的切面[注]
6 圆周长=2π×圆半径圆面积==π×圆半径2 大圆周长=2π×球半径球面积=4π×球半径2球体积=
[注] 与球面只有一个公共点的平面叫做球的切面,这个公共点叫做切点。
类似的,与球面只有一个公共点的直线叫做球的切线,这个公共点也叫做切点。球的切线有以下主要性质:
1. 过切点的球半径垂直于球的切线;
2. 过球面上一点的切线有无限多条,这些切线都在这一点的球的切面内。
常见问题2: 球
问题:
地球半径为R,A、B两地都在北纬45°线上,且A、B的球面距离为 ,求A、B两地经度的差.
解答:
分析:如图,O为球心,O1为北纬45°小圆的圆心,知A、B的球面距离,就可求得∠AOB的弧度数,进而求得线段AB的长,在ΔAO1B中,∠AO1B的大小就是A、B两地的经度差.
解 设O1是北纬45°圈的中心,
∵A、B都在此圈上,
∴O1A=O1B= R.
∵A、B的球面距离为 ,
∴∠AOB= = = ,ΔAOB为等边三角形.
AB=R,在ΔAO1B中,
∵O1A2+O1B2= R2+ R2=R2=AB2,
∴∠AO1B=90°.
∴A、B两地的经度差是90°.
评析:注意搞清纬度和经度的问题,球面距离三步骤的运用是非常重要的问题.
常见问题3: 球
问题:
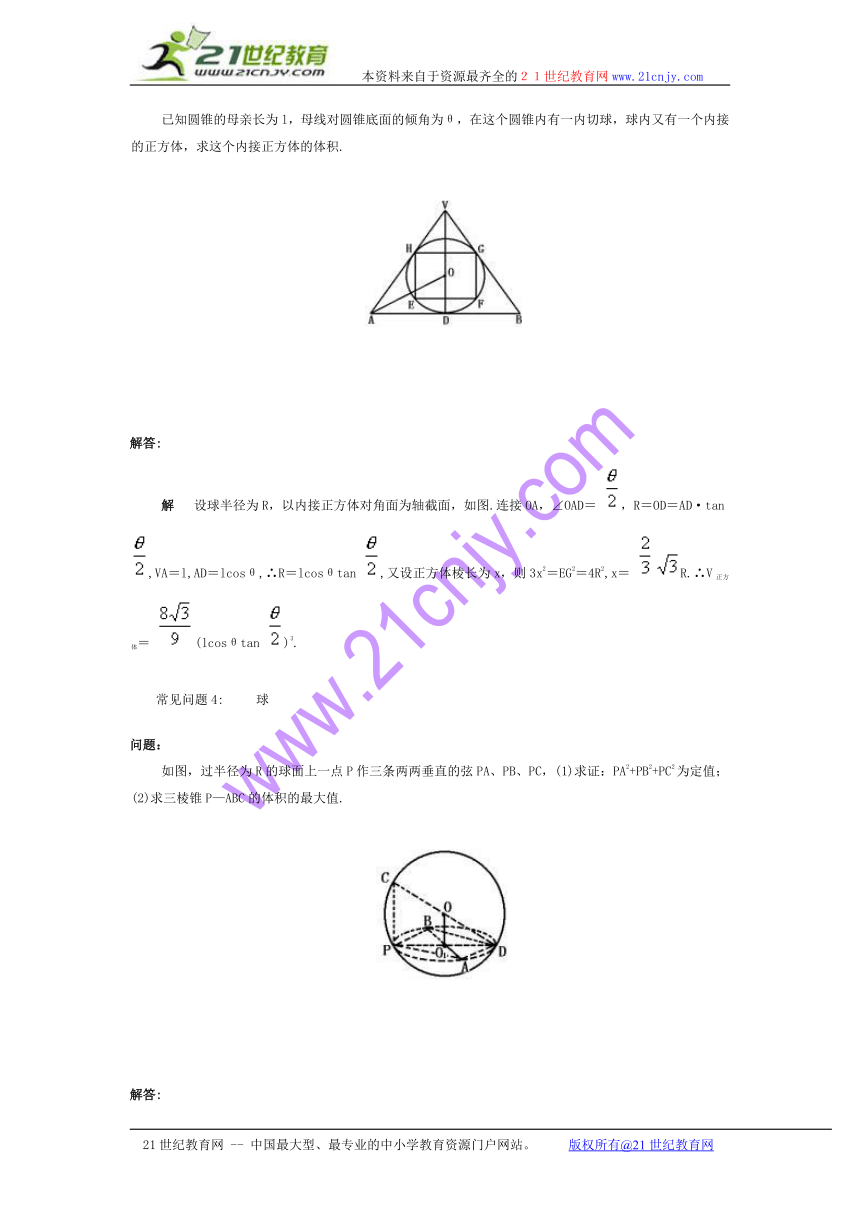
已知圆锥的母亲长为l,母线对圆锥底面的倾角为θ,在这个圆锥内有一内切球,球内又有一个内接的正方体,求这个内接正方体的体积.
解答:
解 设球半径为R,以内接正方体对角面为轴截面,如图.连接OA,∠OAD= ,R=OD=AD·tan ,VA=l,AD=lcosθ,∴R=lcosθtan ,又设正方体棱长为x,则3x2=EG2=4R2,x= R.∴V正方体= (lcosθtan )3.
常见问题4: 球
问题:
如图,过半径为R的球面上一点P作三条两两垂直的弦PA、PB、PC,(1)求证:PA2+PB2+PC2为定值;(2)求三棱锥P—ABC的体积的最大值.
解答:
分析:先选其中两条弦PA、PB,设其确定的平面截球得⊙O1,AB是⊙O1的直径,连PO1并延长交⊙O1于D,PADB是矩形,PD2=AB2=PA2+PB2,然后只要证得PC和PD确定是大圆就可以了.
解 (1)设过PA、PB的平面截球得⊙O1,∵PA⊥PB,
∴AB是⊙O1的直径,连PO1并延长交⊙O1于D,则PADB是矩形,PD2=PA2+PB2.
设O为球心,则OO1⊥平面⊙O1,
∵PC⊥⊙O1平面,
∴OO1∥PC,因此过PC、PD的平面经过球心O,截球得大圆,又PC⊥PD.
∴CD是球的直径.
故 PA2+PB2+PC2=PD2+PC2=CD2=4R2定值.
(2)设PA、PB、PC的长分别为x、y、z,则三棱锥P—ABC的体积V= xyz,
V2= x2y2z2≤ ( )3= · = R6.
∴V≤ R3.
即 V最大= R3.
评析:定值问题可用特殊情况先“探求”,如本题(1)若先考虑PAB是大圆,探求得定值4R2可为(1)的证明指明方向.
球面上任一点对球的直径所张的角等于90°,这应记作很重要的性质.
常见问题5: 球
问题:
求棱长为a的正四面体的外接球和内切球的半径.
解答:
解 如图,作AH⊥底面BCD于H,则AH= a,设内切球的球心为O,半径为r,O点与A、B、C、D相连,得四个锥体,设底面为S,则每个侧面积为S,有4· ·Sr= S·AH,∴r= AH= a,设外接球心为O,半径R,过A点作球的半径交底面ΔCD于H,则H为圆BCD的圆心,求得BH= a,AH= a,由相交弦定理得 a×(2R- a)=( a)2.
解得R= a.
常见问题6: 球
问题:
球面上有3个点,其中任意两点的球面距离都等于大圆周长的 ,经过3个点的小圆的周长为4π,那么这个球的半径为( )
A.4 B.2 C.2 D.
解答:
解 设球半径为R,小圆半径为r,则2πr=4π,∴r=2.如图,设三点A、B、C,O为球心,∠AOB=∠BOC=∠COA= ,又∵OA=OB
∴ΔAOB是等边三角形
同理,ΔBOC、ΔCOA都是等边三角形,得ΔABC为等边三角形.
边长等于球半径R,r为ΔABC的外接圆半径.
r= AB= R
R= r=2
∴应选B.
常见问题7: 球
问题:
已知球面上A、B、C三点的截面和球心的距离都是球半径的一半,且AB=BC=CA=2,则球表面积是( )
A. π B. π C.4π D. π
解答:
解 如图,过ABC三点的截面圆的圆心是O′,球心是O,连结AO′、OO′,则OO′⊥ AO′.ΔABC中,AB=BC=CA=2,故ΔABC为正三角形.
∴AO′= ×2=
设球半径为R,则OA=R,OO′=
在RtΔOAO′中,OA2=O′O2+O′A2,即R2= +( )2
∴R=
∴球面面积为4πR2= π
∴应选A.
说明 因为R=OA>O′A> AB=1,所以球面积S=4πR2>4π.从而选A.
常见问题8: 球
问题:
长方体的一个顶点上的三条棱分别是3、4、5,且它的八个顶点都在同一球面上,这个球的表面积是( )
A.20 π B.25 π C.50π D.200π
解答:
解 正方体的对角线为l,球的半径为R,则l=2R.
得:l2=4R2=32+42+52=50
从而 S球=4πR2=50π
∴应选C.
常见问题9: 球
问题:
在球面上有四个点P、A、B、C.如果PA、PB、PC两两互相垂直,且PA=PB=PC=a,那么这个球的表面积是 .
解答:
解 由已知可得PA、PB、PC实际上就是球内接正方体中交于一点的三条棱,正方体的对角线长就是球的直径,连结过点C的一条对角线CD,则CD过球心O,对角线CD= a.
∴S球表面积=4π·( a)2=3πa2.
常见问题10: 球
问题:
圆柱形容器的内壁底半径为5cm,两个直径为5cm的玻璃小球都浸没于容器的水中,若取出这两个小球,则容器内的水面将下降 cm.
解答:
分析:球的体积等于它在容器中排开水的体积.
解 设取出小球后,容器水平面将下降hcm,两小球体积为V球=2× π×52×h,V1= V球
即 25πh= π ∴h= cm.
∴应填 .
常见问题11: 球
问题:
湖结冰时,一个球漂在其上,取出后(未弄破冰),冰面上留下了一个直径为24cm,深为8cm的空穴,求该球的半径.
解答:
解 设球的半径为R,依题意知截面圆的半径r=12,球心与截面的距离为d=R-8,由截面性质得:r2+d2=R2,即122+(R-8)2=R2.
得R=13 ∴该球半径为13cm.
常见问题12: 球
问题:
在有阳光时,一根长为3米的旗轩垂直于水平地面,它的影长为 米,同时将一个半径为3米的球放在这块水平地面上,如图所示,求球的阴影部分的面积(结果用无理数表示).
解答:
解:由题意知,光线与地面成60°角,设球的阴影部分面积为S,垂直于光线的大圆面积为S′,则Scos30°=S′,并且S′=9π,所以S=6 π(米2)
常见问题13: 球
问题:
设棱锥M—ABCD的底面是正方形,且MA=MD,MA⊥AB,如果ΔAMD的面积为1,试求能够放入这个棱锥的最大球的半径.
解答:
解 ∵AB⊥AD,AB⊥MA,
∴AB⊥平面MAD,
由此,面MAD⊥面AC.
记E是AD的中点,
从而ME⊥AD.
∴ME⊥平面AC ME⊥EF
设球O是与平面MAD、AC、平面MBC都相切的球.
不妨设O∈平面MEF,于是O是ΔMEF的内心.
设球O的半径为r,则r=
设AD=EF=a,∵SΔAMD=1.
∴ME= .MF= ,
r= ≤ = -1
当且仅当a= ,即a= 时,等号成立.
∴当AD=ME= 时,满足条件的球最大半径为 -1.
w.w.w.k.s.5.u.c.o.m
www.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
【关于“球”的常见问题】
常见问题1: 问题:怎样把圆和球的主要性质进行对照?
解答:
答:
圆的主要性质 球的主要性质
1 平面内与定点距离等于定长的点集(轨迹) 空间与定点距离等于定长的点集(轨迹)
2 同圆(或等圆)的半径相等,直径是半径的2倍 同球(或等球)的半径相等,直径是半径的2倍
3 与弦垂直的直径过弦的中点,圆半径2=圆心到弦距离2+弦长的一半2 与截面积垂直的直径过截面圆的圆心,球半径2=球心到截面圆距离2+截面圆的半径2
4 不过圆心的弦小于直径;经过圆心的弦是直径,是最大的弦 不过球心的截得的是球的小圆,其半径和面积都小于球的大圆的半径和面积;经过球心的截面截得的是球的大圆,是最大的截面圆
5 过切点的圆半径垂直于圆的切线 过切点的球半径垂直于球的切面[注]
6 圆周长=2π×圆半径圆面积==π×圆半径2 大圆周长=2π×球半径球面积=4π×球半径2球体积=
[注] 与球面只有一个公共点的平面叫做球的切面,这个公共点叫做切点。
类似的,与球面只有一个公共点的直线叫做球的切线,这个公共点也叫做切点。球的切线有以下主要性质:
1. 过切点的球半径垂直于球的切线;
2. 过球面上一点的切线有无限多条,这些切线都在这一点的球的切面内。
常见问题2: 球
问题:
地球半径为R,A、B两地都在北纬45°线上,且A、B的球面距离为 ,求A、B两地经度的差.
解答:
分析:如图,O为球心,O1为北纬45°小圆的圆心,知A、B的球面距离,就可求得∠AOB的弧度数,进而求得线段AB的长,在ΔAO1B中,∠AO1B的大小就是A、B两地的经度差.
解 设O1是北纬45°圈的中心,
∵A、B都在此圈上,
∴O1A=O1B= R.
∵A、B的球面距离为 ,
∴∠AOB= = = ,ΔAOB为等边三角形.
AB=R,在ΔAO1B中,
∵O1A2+O1B2= R2+ R2=R2=AB2,
∴∠AO1B=90°.
∴A、B两地的经度差是90°.
评析:注意搞清纬度和经度的问题,球面距离三步骤的运用是非常重要的问题.
常见问题3: 球
问题:
已知圆锥的母亲长为l,母线对圆锥底面的倾角为θ,在这个圆锥内有一内切球,球内又有一个内接的正方体,求这个内接正方体的体积.
解答:
解 设球半径为R,以内接正方体对角面为轴截面,如图.连接OA,∠OAD= ,R=OD=AD·tan ,VA=l,AD=lcosθ,∴R=lcosθtan ,又设正方体棱长为x,则3x2=EG2=4R2,x= R.∴V正方体= (lcosθtan )3.
常见问题4: 球
问题:
如图,过半径为R的球面上一点P作三条两两垂直的弦PA、PB、PC,(1)求证:PA2+PB2+PC2为定值;(2)求三棱锥P—ABC的体积的最大值.
解答:
分析:先选其中两条弦PA、PB,设其确定的平面截球得⊙O1,AB是⊙O1的直径,连PO1并延长交⊙O1于D,PADB是矩形,PD2=AB2=PA2+PB2,然后只要证得PC和PD确定是大圆就可以了.
解 (1)设过PA、PB的平面截球得⊙O1,∵PA⊥PB,
∴AB是⊙O1的直径,连PO1并延长交⊙O1于D,则PADB是矩形,PD2=PA2+PB2.
设O为球心,则OO1⊥平面⊙O1,
∵PC⊥⊙O1平面,
∴OO1∥PC,因此过PC、PD的平面经过球心O,截球得大圆,又PC⊥PD.
∴CD是球的直径.
故 PA2+PB2+PC2=PD2+PC2=CD2=4R2定值.
(2)设PA、PB、PC的长分别为x、y、z,则三棱锥P—ABC的体积V= xyz,
V2= x2y2z2≤ ( )3= · = R6.
∴V≤ R3.
即 V最大= R3.
评析:定值问题可用特殊情况先“探求”,如本题(1)若先考虑PAB是大圆,探求得定值4R2可为(1)的证明指明方向.
球面上任一点对球的直径所张的角等于90°,这应记作很重要的性质.
常见问题5: 球
问题:
求棱长为a的正四面体的外接球和内切球的半径.
解答:
解 如图,作AH⊥底面BCD于H,则AH= a,设内切球的球心为O,半径为r,O点与A、B、C、D相连,得四个锥体,设底面为S,则每个侧面积为S,有4· ·Sr= S·AH,∴r= AH= a,设外接球心为O,半径R,过A点作球的半径交底面ΔCD于H,则H为圆BCD的圆心,求得BH= a,AH= a,由相交弦定理得 a×(2R- a)=( a)2.
解得R= a.
常见问题6: 球
问题:
球面上有3个点,其中任意两点的球面距离都等于大圆周长的 ,经过3个点的小圆的周长为4π,那么这个球的半径为( )
A.4 B.2 C.2 D.
解答:
解 设球半径为R,小圆半径为r,则2πr=4π,∴r=2.如图,设三点A、B、C,O为球心,∠AOB=∠BOC=∠COA= ,又∵OA=OB
∴ΔAOB是等边三角形
同理,ΔBOC、ΔCOA都是等边三角形,得ΔABC为等边三角形.
边长等于球半径R,r为ΔABC的外接圆半径.
r= AB= R
R= r=2
∴应选B.
常见问题7: 球
问题:
已知球面上A、B、C三点的截面和球心的距离都是球半径的一半,且AB=BC=CA=2,则球表面积是( )
A. π B. π C.4π D. π
解答:
解 如图,过ABC三点的截面圆的圆心是O′,球心是O,连结AO′、OO′,则OO′⊥ AO′.ΔABC中,AB=BC=CA=2,故ΔABC为正三角形.
∴AO′= ×2=
设球半径为R,则OA=R,OO′=
在RtΔOAO′中,OA2=O′O2+O′A2,即R2= +( )2
∴R=
∴球面面积为4πR2= π
∴应选A.
说明 因为R=OA>O′A> AB=1,所以球面积S=4πR2>4π.从而选A.
常见问题8: 球
问题:
长方体的一个顶点上的三条棱分别是3、4、5,且它的八个顶点都在同一球面上,这个球的表面积是( )
A.20 π B.25 π C.50π D.200π
解答:
解 正方体的对角线为l,球的半径为R,则l=2R.
得:l2=4R2=32+42+52=50
从而 S球=4πR2=50π
∴应选C.
常见问题9: 球
问题:
在球面上有四个点P、A、B、C.如果PA、PB、PC两两互相垂直,且PA=PB=PC=a,那么这个球的表面积是 .
解答:
解 由已知可得PA、PB、PC实际上就是球内接正方体中交于一点的三条棱,正方体的对角线长就是球的直径,连结过点C的一条对角线CD,则CD过球心O,对角线CD= a.
∴S球表面积=4π·( a)2=3πa2.
常见问题10: 球
问题:
圆柱形容器的内壁底半径为5cm,两个直径为5cm的玻璃小球都浸没于容器的水中,若取出这两个小球,则容器内的水面将下降 cm.
解答:
分析:球的体积等于它在容器中排开水的体积.
解 设取出小球后,容器水平面将下降hcm,两小球体积为V球=2× π×52×h,V1= V球
即 25πh= π ∴h= cm.
∴应填 .
常见问题11: 球
问题:
湖结冰时,一个球漂在其上,取出后(未弄破冰),冰面上留下了一个直径为24cm,深为8cm的空穴,求该球的半径.
解答:
解 设球的半径为R,依题意知截面圆的半径r=12,球心与截面的距离为d=R-8,由截面性质得:r2+d2=R2,即122+(R-8)2=R2.
得R=13 ∴该球半径为13cm.
常见问题12: 球
问题:
在有阳光时,一根长为3米的旗轩垂直于水平地面,它的影长为 米,同时将一个半径为3米的球放在这块水平地面上,如图所示,求球的阴影部分的面积(结果用无理数表示).
解答:
解:由题意知,光线与地面成60°角,设球的阴影部分面积为S,垂直于光线的大圆面积为S′,则Scos30°=S′,并且S′=9π,所以S=6 π(米2)
常见问题13: 球
问题:
设棱锥M—ABCD的底面是正方形,且MA=MD,MA⊥AB,如果ΔAMD的面积为1,试求能够放入这个棱锥的最大球的半径.
解答:
解 ∵AB⊥AD,AB⊥MA,
∴AB⊥平面MAD,
由此,面MAD⊥面AC.
记E是AD的中点,
从而ME⊥AD.
∴ME⊥平面AC ME⊥EF
设球O是与平面MAD、AC、平面MBC都相切的球.
不妨设O∈平面MEF,于是O是ΔMEF的内心.
设球O的半径为r,则r=
设AD=EF=a,∵SΔAMD=1.
∴ME= .MF= ,
r= ≤ = -1
当且仅当a= ,即a= 时,等号成立.
∴当AD=ME= 时,满足条件的球最大半径为 -1.
w.w.w.k.s.5.u.c.o.m
www.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
