7.1.1 对顶角、补角、余角 同步练习(含答案)
文档属性
| 名称 | 7.1.1 对顶角、补角、余角 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 433.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 13:25:03 | ||
图片预览

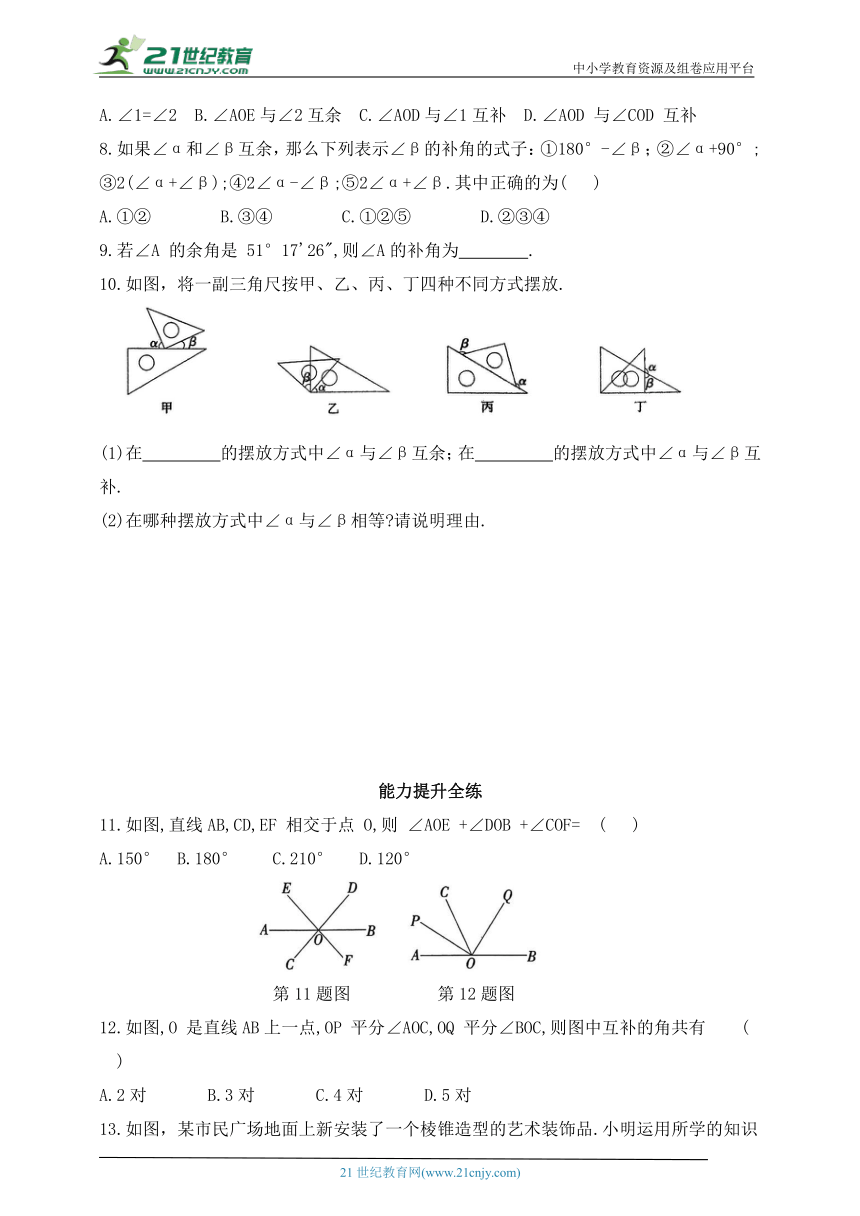
文档简介
中小学教育资源及组卷应用平台
第七章 相交线与平行线
1 两条直线的位置关系
第1课时 对顶角、补角、余角
基础过关全练
知识点 1 两条直线的位置关系
1.在同一平面内,不重合的两条直线的位置关系是 ( )
A.平行 B.相交 C.平行或相交 D.平行、相交或垂直
2.如图,在长方体ABCD-EFGH中,与BC平行的棱是 .
3.举出生活中属于平行线的例子.(写出一个即可)
知识点 2 对顶角的概念与性质
4.下面四个图形中,∠1与∠2是对顶角的图形为(M6207001) ( )
5.如图,直线AB,CD相交于点 O,若∠1=80°,∠2=30°,则∠AOE的度数为( )
A.30° B.50° C.60° D.80°
6.如图,两直线交于点 O,若∠1+∠2=76°,则∠1= °.
知识点 3 互补、互余的概念与性质
7.如图,点 O 在直线AB上,∠COB=∠EOD=90°,下列说法错误的是 ( )
A.∠1=∠2 B.∠AOE与∠2互余 C.∠AOD与∠1互补 D.∠AOD 与∠COD 互补
8.如果∠α和∠β互余,那么下列表示∠β的补角的式子:①180°-∠β;②∠α+90°;③2(∠α+∠β);④2∠α-∠β;⑤2∠α+∠β.其中正确的为( )
A.①② B.③④ C.①②⑤ D.②③④
9.若∠A 的余角是 51°17'26",则∠A的补角为 .
10.如图,将一副三角尺按甲、乙、丙、丁四种不同方式摆放.
(1)在 的摆放方式中∠α与∠β互余;在 的摆放方式中∠α与∠β互补.
(2)在哪种摆放方式中∠α与∠β相等 请说明理由.
能力提升全练
11.如图,直线AB,CD,EF 相交于点 O,则 ∠AOE +∠DOB +∠COF= ( )
A.150° B.180° C.210° D.120°
第11题图 第12题图
12.如图,O 是直线AB上一点,OP 平分∠AOC,OQ 平分∠BOC,则图中互补的角共有 ( )
A.2对 B.3对 C.4对 D.5对
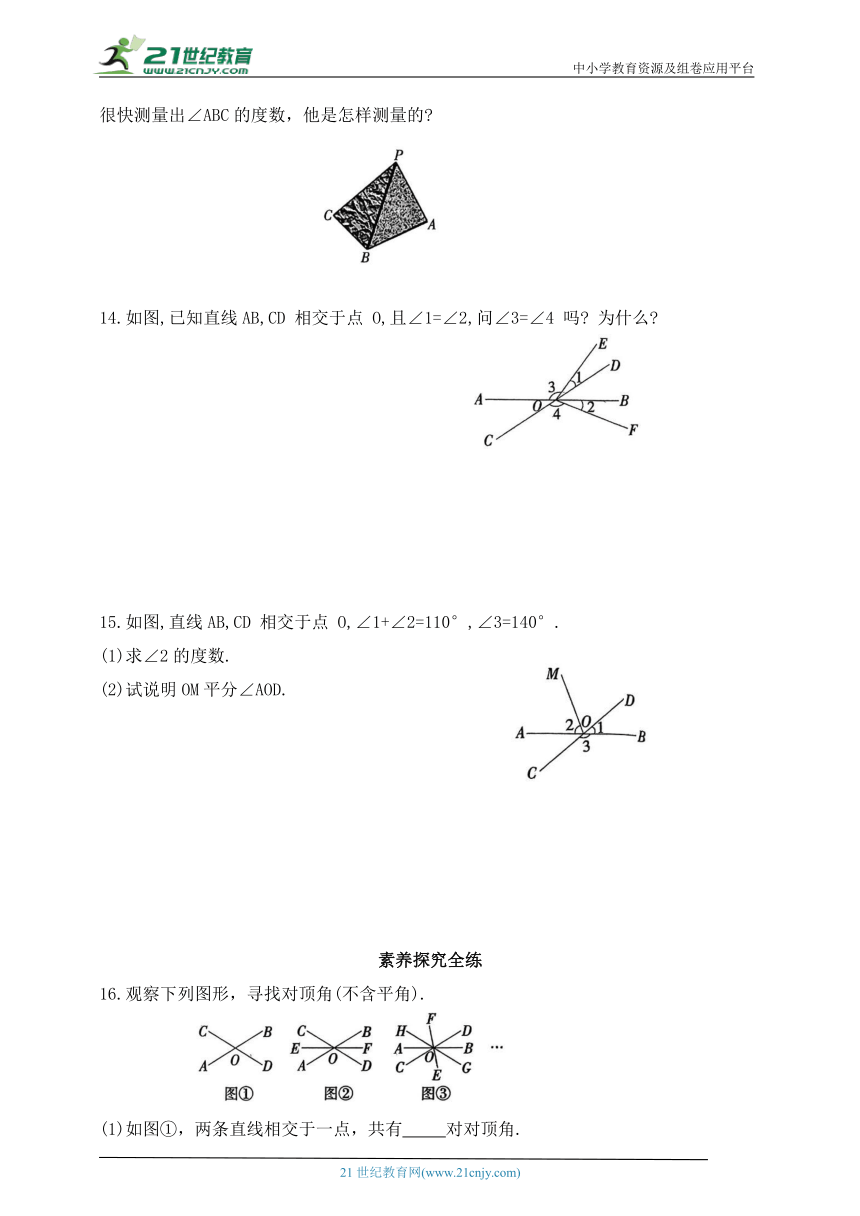
13.如图,某市民广场地面上新安装了一个棱锥造型的艺术装饰品.小明运用所学的知识很快测量出∠ABC的度数,他是怎样测量的
14.如图,已知直线AB,CD 相交于点 O,且∠1=∠2,问∠3=∠4 吗 为什么
15.如图,直线AB,CD 相交于点 O,∠1+∠2=110°,∠3=140°.
(1)求∠2的度数.
(2)试说明OM平分∠AOD.
素养探究全练
16.观察下列图形,寻找对顶角(不含平角).
(1)如图①,两条直线相交于一点,共有 对对顶角.
(2)如图②,三条直线相交于一点,共有 对对顶角.
(3)如图③,四条直线相交于一点,共有 对对顶角.
(4)根据填空结果探究:当n条直线相交于一点时,共有多少对对顶角.
(5)根据探究结果,求1 000 条直线相交于一点时,所构成的对顶角的对数.
参考答案
基础过关全练
1 C在同一平面内,不重合的两条直线只有两种位置关系:平行、相交.故选 C.
2 答案 AD,EH,FG
3 解析 答案不唯一,如:
(1)铁路的铁轨,两条铁轨是平行的;
(2)高速公路上的车道分隔线,相邻的分隔线互相平行;
(3)黑板的上下边缘是平行的.
4 C 选项C中,∠1与∠2有公共顶点且两边互为反向延长线,两个角是对顶角.故选 C.
5 B ∵ ∠AOD=∠1=80°,∴ ∠AOE=∠AOD-∠2= 故选 B.
6 答案 38
解析 ∵两直线交于点O,∴∠1=∠2.∵∠1+∠2=76°,∴∠1=38°.
7 D∵∠COB=∠EOD=90°,∴ ∠1+∠COD=∠2+∠COD=90°,∴ ∠1 =∠2,故 A 选项说法正确;∵∠AOE+∠1=90°,∴ ∠AOE+∠2=90°,即∠AOE与∠2互余,故 B 选项说法正确;∵∠AOD+∠2=180°,∴∠AOD+∠1=180°,即∠AOD 与∠1互补,故C选项说法正确;无法判断∠AOD 与 是否互补,D选项说法错误.故选 D.(∠α和∠β互余,∴ ∠α+∠β=90°,∴ ∠β=90°-∠α.∵ ∠β的补角为180°-∠β,..其补角还可以表示为180°-(90°-∠α)=∠α+90°.∵ ∠α+∠β=90°,∴2∠α+2∠β=180°,.. ∠β的补角还可以表示为2∠α+2∠β-∠β=2∠α+∠β,故①②⑤正确.故选 C.
9 答案 141°17'26"
解析 ∠A 的补角为1 141°17'26".
10 解析 (1)在甲中,根据平角的定义得∠α+90°+∠β=180°,∴∠α+∠β=90°,即∠α与∠β互余;在丁中,根据图形可知∠α与∠β是邻补角,∴∠α+∠β=180°,即∠α与∠β互补.故答案为甲;丁.
(2)在乙、丙的摆放方式中∠α与∠β相等,理由如下:
在乙中:如图,∵∠α和∠β都是∠1的余角,∴ ∠α=∠β.
在丙中: 135°,∴ ∠α=∠β.
能力提升全练
11 B ∵ ∠COF 与∠DOE 是对 顶角,∴ ∠COF =∠DOE,∴∠AOE+∠DOB+∠COF=∠AOE+∠DOB+∠DOE=180°.故选 B.
12 D∵ OP 平分∠AOC,OQ 平分∠BOC,∴ ∠AOP=∠COP,∠BOQ=∠COQ.∵ ∠AOP+∠BOP=180°,∠BOQ+∠AOQ= 180°,∴ ∠COP +∠BOP = 180°,∠COQ+∠AOQ=180°.又∵ ∠AOC+∠COB=180°,∴互补的角有∠AOP 和∠BOP,∠COP 和∠BOP,∠BOQ 和 ∠AOQ, ∠COQ 和 ∠AOQ, ∠AOC 和∠COB,共5对.故选 D.
13 解析 (测量方法不唯一,以下解法仅供参考)如图所示:
【解法一】利用邻补角求解:先测量出∠CBD(或∠ABE)的度数,再由邻补角的性质,得∠ABC=180°-∠CBD(或
【解法二】利用对顶角求解:先测量出∠DBE 的度数,再利用对顶角相等,得 ∠ABC=∠DBE.
14 解析 ∠3=∠4,理由如下:
∵∠1=∠2,∴∠1+∠BOD=∠2+∠BOD,即∠EOB=∠DOF.
又∠3与∠EOB互补,∠4与∠DOF互补,∠3=∠4.
15 解析 (1)∵∠3=140°,∴∠AOD=∠3=140°.
∵∠1+∠AOD=180°,∴ ∠1=180°-∠AOD=180°-140°=40°.
∵∠1+∠2=110°,
(2)∵∠1+∠2=110°,
∴∠2=70°=∠MOD,∴OM平分∠AOD.
素养探究全练
16 解析 (1)题图①中对顶角是∠AOC与∠BOD,∠AOD与∠BOC,共有2对对顶角(2=1×2).故答案为2.
(2)题图②中对顶角是∠AOC 与∠DOB,∠COF与∠DOE,∠BOF 与∠AOE,∠AOF 与∠BOE,∠BOC与∠AOD,∠DOF与∠COE,共有6对对顶角(6=2×3).故答案为6.
(3)题图③中4条直线交于O 点,对顶角的数目是在前三条直线组合成的6对对顶角的基础上加上第四条直线与前3条直线组合成的6对对顶角,∴题图③中共有 12 对对顶角(12=3×4).故答案为12.
(4)若有n条直线相交于一点,则可形成n(n-1)对对顶角.
(5)根据(4)得,1000条直线相交于一点时,所构成的对顶角有1000×999=999000(对).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章 相交线与平行线
1 两条直线的位置关系
第1课时 对顶角、补角、余角
基础过关全练
知识点 1 两条直线的位置关系
1.在同一平面内,不重合的两条直线的位置关系是 ( )
A.平行 B.相交 C.平行或相交 D.平行、相交或垂直
2.如图,在长方体ABCD-EFGH中,与BC平行的棱是 .
3.举出生活中属于平行线的例子.(写出一个即可)
知识点 2 对顶角的概念与性质
4.下面四个图形中,∠1与∠2是对顶角的图形为(M6207001) ( )
5.如图,直线AB,CD相交于点 O,若∠1=80°,∠2=30°,则∠AOE的度数为( )
A.30° B.50° C.60° D.80°
6.如图,两直线交于点 O,若∠1+∠2=76°,则∠1= °.
知识点 3 互补、互余的概念与性质
7.如图,点 O 在直线AB上,∠COB=∠EOD=90°,下列说法错误的是 ( )
A.∠1=∠2 B.∠AOE与∠2互余 C.∠AOD与∠1互补 D.∠AOD 与∠COD 互补
8.如果∠α和∠β互余,那么下列表示∠β的补角的式子:①180°-∠β;②∠α+90°;③2(∠α+∠β);④2∠α-∠β;⑤2∠α+∠β.其中正确的为( )
A.①② B.③④ C.①②⑤ D.②③④
9.若∠A 的余角是 51°17'26",则∠A的补角为 .
10.如图,将一副三角尺按甲、乙、丙、丁四种不同方式摆放.
(1)在 的摆放方式中∠α与∠β互余;在 的摆放方式中∠α与∠β互补.
(2)在哪种摆放方式中∠α与∠β相等 请说明理由.
能力提升全练
11.如图,直线AB,CD,EF 相交于点 O,则 ∠AOE +∠DOB +∠COF= ( )
A.150° B.180° C.210° D.120°
第11题图 第12题图
12.如图,O 是直线AB上一点,OP 平分∠AOC,OQ 平分∠BOC,则图中互补的角共有 ( )
A.2对 B.3对 C.4对 D.5对
13.如图,某市民广场地面上新安装了一个棱锥造型的艺术装饰品.小明运用所学的知识很快测量出∠ABC的度数,他是怎样测量的
14.如图,已知直线AB,CD 相交于点 O,且∠1=∠2,问∠3=∠4 吗 为什么
15.如图,直线AB,CD 相交于点 O,∠1+∠2=110°,∠3=140°.
(1)求∠2的度数.
(2)试说明OM平分∠AOD.
素养探究全练
16.观察下列图形,寻找对顶角(不含平角).
(1)如图①,两条直线相交于一点,共有 对对顶角.
(2)如图②,三条直线相交于一点,共有 对对顶角.
(3)如图③,四条直线相交于一点,共有 对对顶角.
(4)根据填空结果探究:当n条直线相交于一点时,共有多少对对顶角.
(5)根据探究结果,求1 000 条直线相交于一点时,所构成的对顶角的对数.
参考答案
基础过关全练
1 C在同一平面内,不重合的两条直线只有两种位置关系:平行、相交.故选 C.
2 答案 AD,EH,FG
3 解析 答案不唯一,如:
(1)铁路的铁轨,两条铁轨是平行的;
(2)高速公路上的车道分隔线,相邻的分隔线互相平行;
(3)黑板的上下边缘是平行的.
4 C 选项C中,∠1与∠2有公共顶点且两边互为反向延长线,两个角是对顶角.故选 C.
5 B ∵ ∠AOD=∠1=80°,∴ ∠AOE=∠AOD-∠2= 故选 B.
6 答案 38
解析 ∵两直线交于点O,∴∠1=∠2.∵∠1+∠2=76°,∴∠1=38°.
7 D∵∠COB=∠EOD=90°,∴ ∠1+∠COD=∠2+∠COD=90°,∴ ∠1 =∠2,故 A 选项说法正确;∵∠AOE+∠1=90°,∴ ∠AOE+∠2=90°,即∠AOE与∠2互余,故 B 选项说法正确;∵∠AOD+∠2=180°,∴∠AOD+∠1=180°,即∠AOD 与∠1互补,故C选项说法正确;无法判断∠AOD 与 是否互补,D选项说法错误.故选 D.(∠α和∠β互余,∴ ∠α+∠β=90°,∴ ∠β=90°-∠α.∵ ∠β的补角为180°-∠β,..其补角还可以表示为180°-(90°-∠α)=∠α+90°.∵ ∠α+∠β=90°,∴2∠α+2∠β=180°,.. ∠β的补角还可以表示为2∠α+2∠β-∠β=2∠α+∠β,故①②⑤正确.故选 C.
9 答案 141°17'26"
解析 ∠A 的补角为1 141°17'26".
10 解析 (1)在甲中,根据平角的定义得∠α+90°+∠β=180°,∴∠α+∠β=90°,即∠α与∠β互余;在丁中,根据图形可知∠α与∠β是邻补角,∴∠α+∠β=180°,即∠α与∠β互补.故答案为甲;丁.
(2)在乙、丙的摆放方式中∠α与∠β相等,理由如下:
在乙中:如图,∵∠α和∠β都是∠1的余角,∴ ∠α=∠β.
在丙中: 135°,∴ ∠α=∠β.
能力提升全练
11 B ∵ ∠COF 与∠DOE 是对 顶角,∴ ∠COF =∠DOE,∴∠AOE+∠DOB+∠COF=∠AOE+∠DOB+∠DOE=180°.故选 B.
12 D∵ OP 平分∠AOC,OQ 平分∠BOC,∴ ∠AOP=∠COP,∠BOQ=∠COQ.∵ ∠AOP+∠BOP=180°,∠BOQ+∠AOQ= 180°,∴ ∠COP +∠BOP = 180°,∠COQ+∠AOQ=180°.又∵ ∠AOC+∠COB=180°,∴互补的角有∠AOP 和∠BOP,∠COP 和∠BOP,∠BOQ 和 ∠AOQ, ∠COQ 和 ∠AOQ, ∠AOC 和∠COB,共5对.故选 D.
13 解析 (测量方法不唯一,以下解法仅供参考)如图所示:
【解法一】利用邻补角求解:先测量出∠CBD(或∠ABE)的度数,再由邻补角的性质,得∠ABC=180°-∠CBD(或
【解法二】利用对顶角求解:先测量出∠DBE 的度数,再利用对顶角相等,得 ∠ABC=∠DBE.
14 解析 ∠3=∠4,理由如下:
∵∠1=∠2,∴∠1+∠BOD=∠2+∠BOD,即∠EOB=∠DOF.
又∠3与∠EOB互补,∠4与∠DOF互补,∠3=∠4.
15 解析 (1)∵∠3=140°,∴∠AOD=∠3=140°.
∵∠1+∠AOD=180°,∴ ∠1=180°-∠AOD=180°-140°=40°.
∵∠1+∠2=110°,
(2)∵∠1+∠2=110°,
∴∠2=70°=∠MOD,∴OM平分∠AOD.
素养探究全练
16 解析 (1)题图①中对顶角是∠AOC与∠BOD,∠AOD与∠BOC,共有2对对顶角(2=1×2).故答案为2.
(2)题图②中对顶角是∠AOC 与∠DOB,∠COF与∠DOE,∠BOF 与∠AOE,∠AOF 与∠BOE,∠BOC与∠AOD,∠DOF与∠COE,共有6对对顶角(6=2×3).故答案为6.
(3)题图③中4条直线交于O 点,对顶角的数目是在前三条直线组合成的6对对顶角的基础上加上第四条直线与前3条直线组合成的6对对顶角,∴题图③中共有 12 对对顶角(12=3×4).故答案为12.
(4)若有n条直线相交于一点,则可形成n(n-1)对对顶角.
(5)根据(4)得,1000条直线相交于一点时,所构成的对顶角有1000×999=999000(对).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
