7.3.1 平行线的性质 同步练习(含答案)
文档属性
| 名称 | 7.3.1 平行线的性质 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 439.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 14:31:44 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第七章 相交线与平行线
3 平行线的性质
第1课时 平行线的性质
基础过关全练
知识点1 平行线的性质
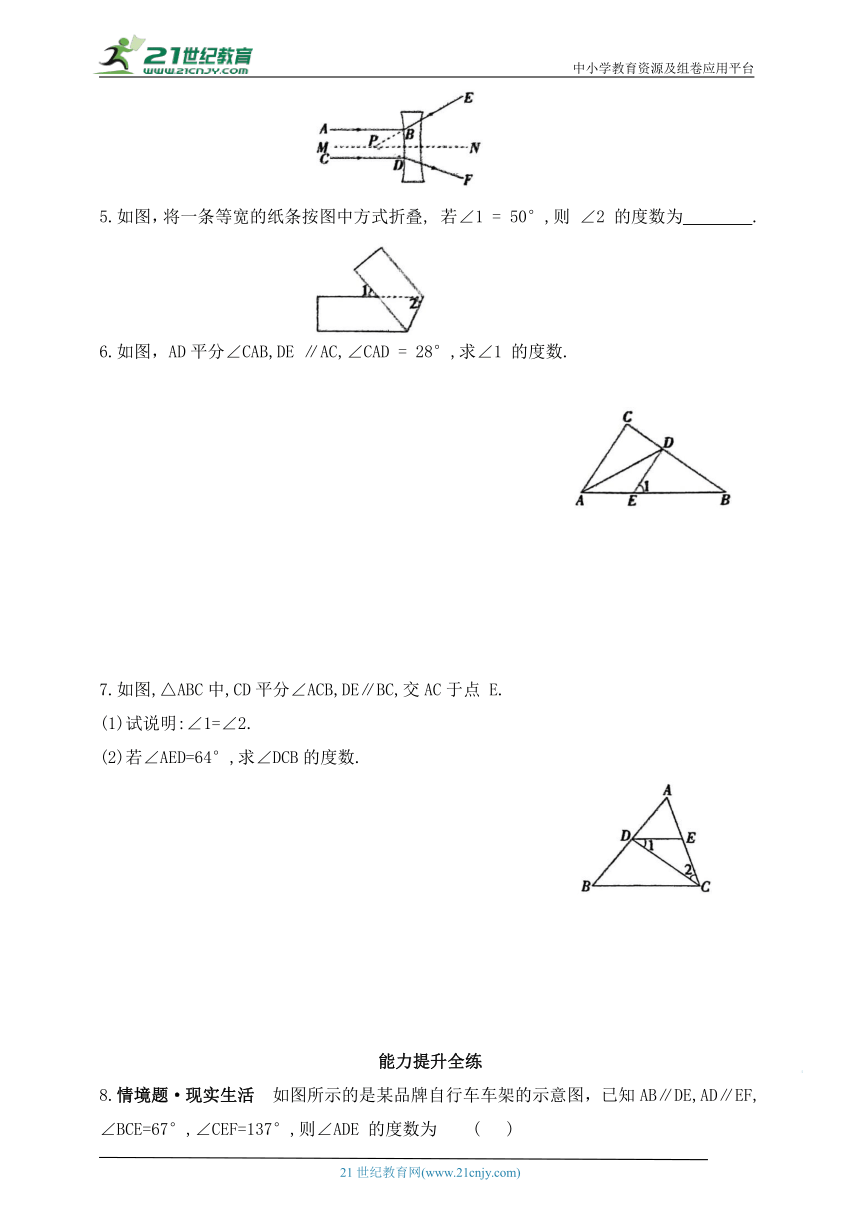
1.如图,AB∥CD,若∠1=125°,则∠2的度数为 ( )
A.35° B.45° C.55° D.125°
第1题图 第2题图
2.如图,AD 是∠EAC 的平分线,AD∥BC,∠BAC=100°,则∠C的度数是 ( )
A.50° B.40° C.35° D.45°
3.一题多变 小明将一块直角三角尺摆放在直尺上,如图,若∠1=55°,则∠2的度数为 ( )
A.25° B.35° C.45° D.55°
[变式]如图,把一块含有45°角的直角三角尺的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是 .
4.跨物理·凹透镜 如图,平行于主光轴 MN 的光线 AB 和 CD 经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴 MN 上一点 P.若∠ABE = 150°,∠CDF=160°,则∠EPF 的度数是 .
5.如图,将一条等宽的纸条按图中方式折叠, 若∠1 = 50°,则 ∠2 的度数为 .
6.如图,AD平分∠CAB,DE ∥AC,∠CAD = 28°,求∠1 的度数.
7.如图,△ABC中,CD平分∠ACB,DE∥BC,交AC于点 E.
(1)试说明:∠1=∠2.
(2)若∠AED=64°,求∠DCB的度数.
能力提升全练
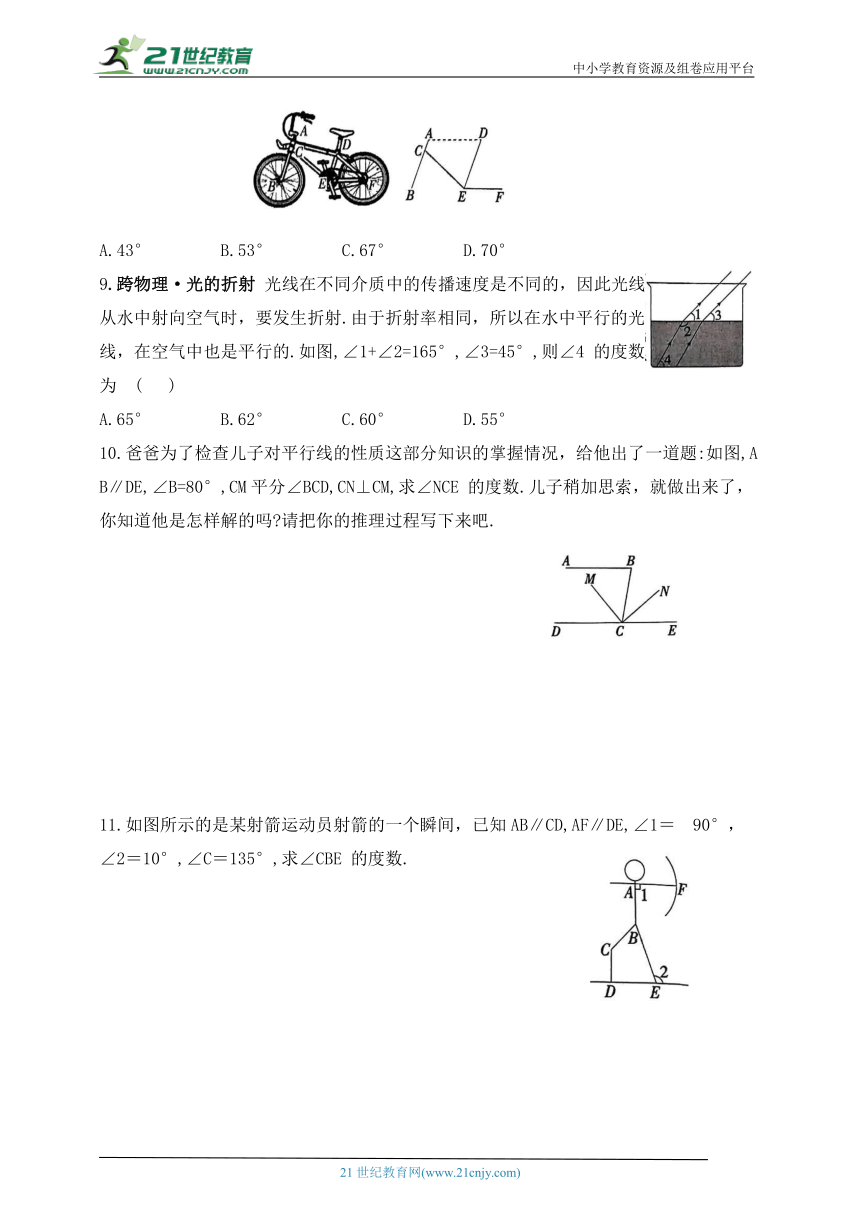
8.情境题·现实生活 如图所示的是某品牌自行车车架的示意图,已知AB∥DE,AD∥EF,∠BCE=67°,∠CEF=137°,则∠ADE 的度数为 ( )
A.43° B.53° C.67° D.70°
9.跨物理·光的折射 光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,∠1+∠2=165°,∠3=45°,则∠4 的度数为 ( )
A.65° B.62° C.60° D.55°
10.爸爸为了检查儿子对平行线的性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE 的度数.儿子稍加思索,就做出来了,你知道他是怎样解的吗 请把你的推理过程写下来吧.
11.如图所示的是某射箭运动员射箭的一个瞬间,已知AB∥CD,AF∥DE,∠1= 90°, ∠2=10°,∠C=135°,求∠CBE 的度数.
素养探究全练
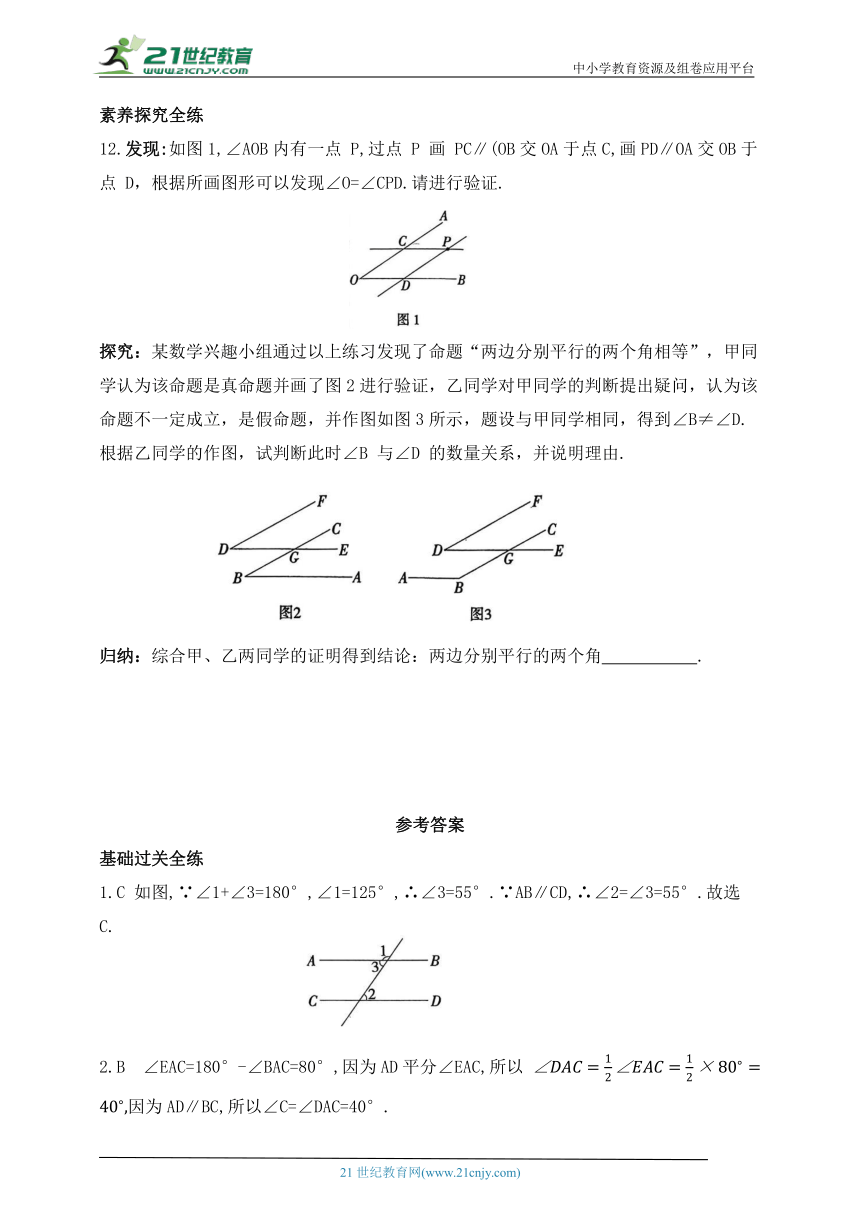
12.发现:如图1,∠AOB内有一点 P,过点 P 画 PC∥(OB交OA于点C,画PD∥OA交OB于点 D,根据所画图形可以发现∠O=∠CPD.请进行验证.
探究:某数学兴趣小组通过以上练习发现了命题“两边分别平行的两个角相等”,甲同学认为该命题是真命题并画了图2进行验证,乙同学对甲同学的判断提出疑问,认为该命题不一定成立,是假命题,并作图如图3所示,题设与甲同学相同,得到∠B≠∠D.根据乙同学的作图,试判断此时∠B 与∠D 的数量关系,并说明理由.
归纳:综合甲、乙两同学的证明得到结论:两边分别平行的两个角 .
参考答案
基础过关全练
1.C 如图,∵∠1+∠3=180°,∠1=125°,∴∠3=55°.∵AB∥CD,∴∠2=∠3=55°.故选 C.
2.B ∠EAC=180°-∠BAC=80°,因为AD平分∠EAC,所以 因为AD∥BC,所以∠C=∠DAC=40°.
3.B 如图所示:
∵直尺的两条长边平行,∠1=55°,∴ ∠3=∠1=55°,
∴∠2=180°-90°-55°=35°.故选 B.
[变式] 答案 25°
解析 如图,∵直尺的两条长边平行,∴∠1=∠3.
∵∠3+∠2=45°,∴ ∠1+∠2=45°.∵∠1 = 20°,∴ ∠2=25°.
4.答案 50°
解析 ∵ ∠ABE=150°,∴ ∠ABP=30°.
∵ ∠CDF=160°,∴∠CDP=20°.
∵AB∥MN∥CD,∴ ∠BPN=∠ABP = 30°,∠NPD = ∠CDP = 20°,
∴ ∠EPF =∠EPN+∠NPF=50°.
5.答案 65°
解析 如图,∵a∥b,∴∠3=∠1=50°,∠2=∠5.由折叠可知,∠4=∠5.
又∠3+∠4+∠5=180°,∴ ∠5=
故答案为65°.
方法归纳
解决平行线中的折叠问题的一般步骤:第一步:还原;第二步:标出所有相等的角;第三步:找内错角(相等)、同位角(相等)和同旁内角(互补);第四步:计算.
6.解析 ∵ DE∥AC,∴∠1=∠CAB,
∵AD平分∠CAB,∴∠CAB=2∠CAD,∴∠1=2∠CAD=2×28°=56°.
7.解析 (1)证明:∵ CD平分∠ACB,∴ ∠BCD=∠2.
∵DE∥BC,∴∠BCD=∠1,∴∠1=∠2.
(2)∵DE∥BC,∠AED=64°,∴ ∠ACB=∠AED=64°.
∵CD平分∠ACB,∴
能力提升全练
8.D ∵AB∥DE,∴∠BCE=∠DEC=67°
∵∠CEF=137°,∴∠DEF=∠CEF-∠DEC=70°.
∵AD∥EF,∴ ∠ADE=∠DEF=70°.故选 D.
9.C 如图,由题意,得a∥b,c∥d,∴∠1=∠3=45°,∠2+∠4=180°.
∵∠1+∠2=165°,∴∠2=165°-45°=120°,
.故选 C.
10.解析 ∵AB∥DE,∴∠B+∠DCB=180°,
∵CM平分∠BCD,
∵CM⊥CN,∴∠MCN=90°,
11.解析 如图,延长AB 交 DE于 K,
∵AF∥DE,∴∠BKE+∠1=180°,
∵∠1=90°,∴∠BKE=90°,
∵∠2=110°,
∵AB∥CD,∴∠C+∠CBK=180°,
∵∠C=135°,∴∠CBK=45°,∴∠CBE=∠CBK+∠KBE=65°.
素养探究全练
12.解析 发现:∵CP∥OB,∴∠O=∠ACP.
∵PD∥OA,∴∠CPD=∠ACP,∴∠O=∠CPD.
探究:∠D+∠B=180°.
理由:题图3中,∵DF∥BC,∴∠D=∠DGB.
∵DE∥BA,∴∠B+∠DGB=180°,∴∠D+∠B=180°.
归纳:两边分别平行的两个角相等或互补.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章 相交线与平行线
3 平行线的性质
第1课时 平行线的性质
基础过关全练
知识点1 平行线的性质
1.如图,AB∥CD,若∠1=125°,则∠2的度数为 ( )
A.35° B.45° C.55° D.125°
第1题图 第2题图
2.如图,AD 是∠EAC 的平分线,AD∥BC,∠BAC=100°,则∠C的度数是 ( )
A.50° B.40° C.35° D.45°
3.一题多变 小明将一块直角三角尺摆放在直尺上,如图,若∠1=55°,则∠2的度数为 ( )
A.25° B.35° C.45° D.55°
[变式]如图,把一块含有45°角的直角三角尺的两个顶点放在直尺的对边上.如果∠1=20°,那么∠2的度数是 .
4.跨物理·凹透镜 如图,平行于主光轴 MN 的光线 AB 和 CD 经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴 MN 上一点 P.若∠ABE = 150°,∠CDF=160°,则∠EPF 的度数是 .
5.如图,将一条等宽的纸条按图中方式折叠, 若∠1 = 50°,则 ∠2 的度数为 .
6.如图,AD平分∠CAB,DE ∥AC,∠CAD = 28°,求∠1 的度数.
7.如图,△ABC中,CD平分∠ACB,DE∥BC,交AC于点 E.
(1)试说明:∠1=∠2.
(2)若∠AED=64°,求∠DCB的度数.
能力提升全练
8.情境题·现实生活 如图所示的是某品牌自行车车架的示意图,已知AB∥DE,AD∥EF,∠BCE=67°,∠CEF=137°,则∠ADE 的度数为 ( )
A.43° B.53° C.67° D.70°
9.跨物理·光的折射 光线在不同介质中的传播速度是不同的,因此光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,∠1+∠2=165°,∠3=45°,则∠4 的度数为 ( )
A.65° B.62° C.60° D.55°
10.爸爸为了检查儿子对平行线的性质这部分知识的掌握情况,给他出了一道题:如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE 的度数.儿子稍加思索,就做出来了,你知道他是怎样解的吗 请把你的推理过程写下来吧.
11.如图所示的是某射箭运动员射箭的一个瞬间,已知AB∥CD,AF∥DE,∠1= 90°, ∠2=10°,∠C=135°,求∠CBE 的度数.
素养探究全练
12.发现:如图1,∠AOB内有一点 P,过点 P 画 PC∥(OB交OA于点C,画PD∥OA交OB于点 D,根据所画图形可以发现∠O=∠CPD.请进行验证.
探究:某数学兴趣小组通过以上练习发现了命题“两边分别平行的两个角相等”,甲同学认为该命题是真命题并画了图2进行验证,乙同学对甲同学的判断提出疑问,认为该命题不一定成立,是假命题,并作图如图3所示,题设与甲同学相同,得到∠B≠∠D.根据乙同学的作图,试判断此时∠B 与∠D 的数量关系,并说明理由.
归纳:综合甲、乙两同学的证明得到结论:两边分别平行的两个角 .
参考答案
基础过关全练
1.C 如图,∵∠1+∠3=180°,∠1=125°,∴∠3=55°.∵AB∥CD,∴∠2=∠3=55°.故选 C.
2.B ∠EAC=180°-∠BAC=80°,因为AD平分∠EAC,所以 因为AD∥BC,所以∠C=∠DAC=40°.
3.B 如图所示:
∵直尺的两条长边平行,∠1=55°,∴ ∠3=∠1=55°,
∴∠2=180°-90°-55°=35°.故选 B.
[变式] 答案 25°
解析 如图,∵直尺的两条长边平行,∴∠1=∠3.
∵∠3+∠2=45°,∴ ∠1+∠2=45°.∵∠1 = 20°,∴ ∠2=25°.
4.答案 50°
解析 ∵ ∠ABE=150°,∴ ∠ABP=30°.
∵ ∠CDF=160°,∴∠CDP=20°.
∵AB∥MN∥CD,∴ ∠BPN=∠ABP = 30°,∠NPD = ∠CDP = 20°,
∴ ∠EPF =∠EPN+∠NPF=50°.
5.答案 65°
解析 如图,∵a∥b,∴∠3=∠1=50°,∠2=∠5.由折叠可知,∠4=∠5.
又∠3+∠4+∠5=180°,∴ ∠5=
故答案为65°.
方法归纳
解决平行线中的折叠问题的一般步骤:第一步:还原;第二步:标出所有相等的角;第三步:找内错角(相等)、同位角(相等)和同旁内角(互补);第四步:计算.
6.解析 ∵ DE∥AC,∴∠1=∠CAB,
∵AD平分∠CAB,∴∠CAB=2∠CAD,∴∠1=2∠CAD=2×28°=56°.
7.解析 (1)证明:∵ CD平分∠ACB,∴ ∠BCD=∠2.
∵DE∥BC,∴∠BCD=∠1,∴∠1=∠2.
(2)∵DE∥BC,∠AED=64°,∴ ∠ACB=∠AED=64°.
∵CD平分∠ACB,∴
能力提升全练
8.D ∵AB∥DE,∴∠BCE=∠DEC=67°
∵∠CEF=137°,∴∠DEF=∠CEF-∠DEC=70°.
∵AD∥EF,∴ ∠ADE=∠DEF=70°.故选 D.
9.C 如图,由题意,得a∥b,c∥d,∴∠1=∠3=45°,∠2+∠4=180°.
∵∠1+∠2=165°,∴∠2=165°-45°=120°,
.故选 C.
10.解析 ∵AB∥DE,∴∠B+∠DCB=180°,
∵CM平分∠BCD,
∵CM⊥CN,∴∠MCN=90°,
11.解析 如图,延长AB 交 DE于 K,
∵AF∥DE,∴∠BKE+∠1=180°,
∵∠1=90°,∴∠BKE=90°,
∵∠2=110°,
∵AB∥CD,∴∠C+∠CBK=180°,
∵∠C=135°,∴∠CBK=45°,∴∠CBE=∠CBK+∠KBE=65°.
素养探究全练
12.解析 发现:∵CP∥OB,∴∠O=∠ACP.
∵PD∥OA,∴∠CPD=∠ACP,∴∠O=∠CPD.
探究:∠D+∠B=180°.
理由:题图3中,∵DF∥BC,∴∠D=∠DGB.
∵DE∥BA,∴∠B+∠DGB=180°,∴∠D+∠B=180°.
归纳:两边分别平行的两个角相等或互补.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
