7.3.2 平行线的性质与判定 同步练习(含答案)
文档属性
| 名称 | 7.3.2 平行线的性质与判定 同步练习(含答案) | 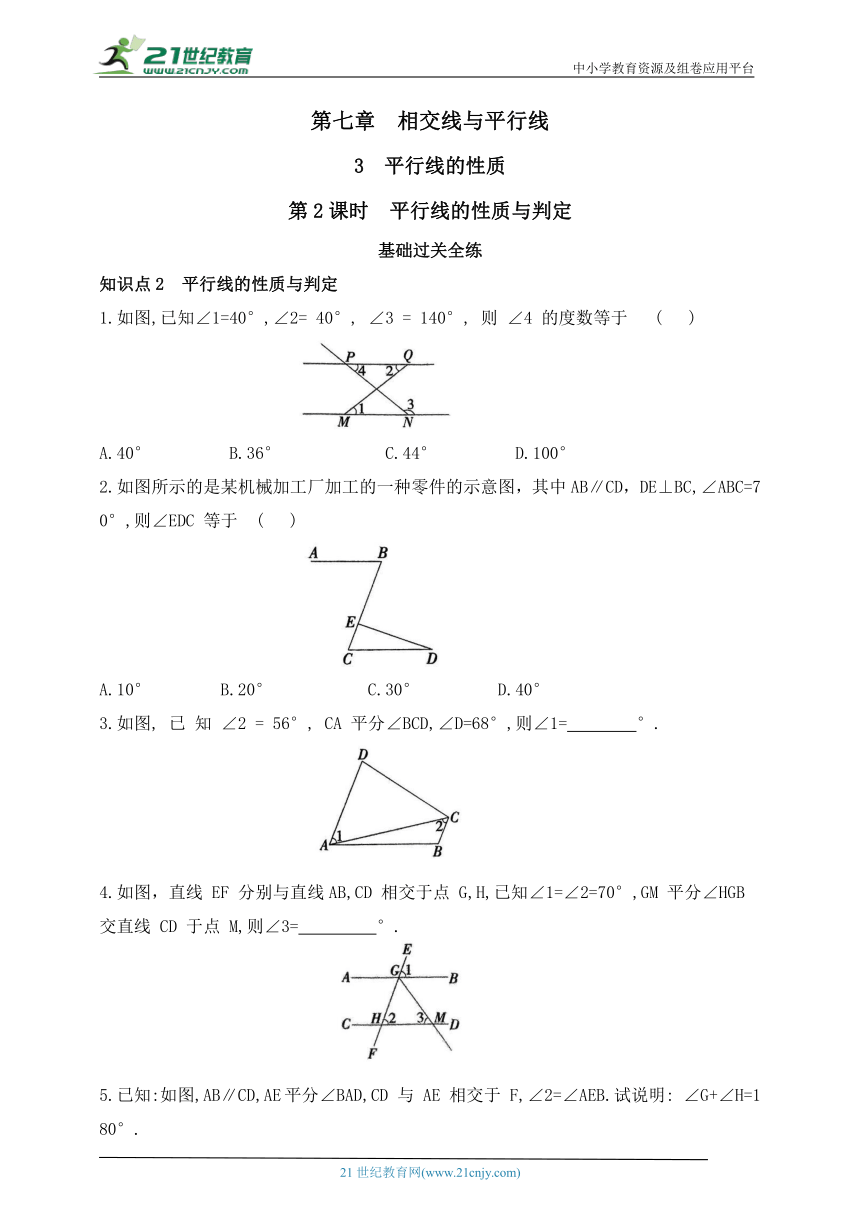 | |
| 格式 | docx | ||
| 文件大小 | 415.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 14:30:40 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第七章 相交线与平行线
3 平行线的性质
第2课时 平行线的性质与判定
基础过关全练
知识点2 平行线的性质与判定
1.如图,已知∠1=40°,∠2= 40°, ∠3 = 140°, 则 ∠4 的度数等于 ( )
A.40° B.36° C.44° D.100°
2.如图所示的是某机械加工厂加工的一种零件的示意图,其中AB∥CD,DE⊥BC,∠ABC=70°,则∠EDC 等于 ( )
A.10° B.20° C.30° D.40°
3.如图, 已 知 ∠2 = 56°, CA 平分∠BCD,∠D=68°,则∠1= °.
4.如图,直线 EF 分别与直线AB,CD 相交于点 G,H,已知∠1=∠2=70°,GM 平分∠HGB 交直线 CD 于点 M,则∠3= °.
5.已知:如图,AB∥CD,AE平分∠BAD,CD 与 AE 相交于 F,∠2=∠AEB.试说明: ∠G+∠H=180°.
能力提升全练
6.情境题·现实生活 小林乘车进入车库时仔细观察了车库门口的曲臂直杆道闸,并抽象出如图所示的模型,已知AB垂直于水平地面AE.当车牌被自动识别后,曲臂直杆道闸的BC段绕点B 缓慢向上旋转,CD 段则一直保持水平状态上升(即CD 与 AE 始终平行),在该过程中∠ABC+∠BCD 始终等于 ( )
A.180° B.250° C.270° D.360°
7.跨物理,凸透镜 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心0的光线相交于点 P,点 F为焦点.若∠2=30°,∠3=55°,则∠1 的度数为 ( )
A.145° B.150° C.135° D.160°
8.如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断 BF 与AC的位置关系,并说明理由.
9.如图,放置在水平操场上的篮球架的横梁 EF 始终平行于AB,主柱AD垂直于地面,EF 与上拉杆 CF 形成的角为∠F,且∠F=150°,可以通过调整 CF和后拉杆BC的位置来调整篮筐的高度,若通过调整使 EF 上升到 GH 的位置,且 GH∥AB,∠CDB=35°,点 H,D,B在同一直线上,求∠H的度数.
素养探究全练
10.如图①,已知AD∥BC(AB>AD),∠B=∠D=120°.
(1)AB与CD平行吗 为什么
(2)若点E,F在线段 CD上,且满足AC平分∠BAE,AF 平分∠DAE,如图②,求∠FAC的度数.
(3)若点 E 在直线 CD 上,且满足∠EAC= 求∠ACD: ∠AED 的值(请自己画出正确图形,并解答).
参考答案
基础过关全练
1.A ∵∠1=40°,∠2=40°,∴∠1=∠2,∴PQ∥MN,∴ ∠3+∠4=180°.
∵∠3=140°,∴∠4=40°.故选 A.
2.B 如图,作EF∥AB,
∵AB∥CD,∴EF∥AB∥CD.
∵∠ABC=70°,∴ ∠BEF=∠ABC=70°.
∵ DE⊥BC,∴∠BED=90°,∴∠FED=90°-70°=20°,
∵ EF∥CD,.∠EDC=∠FED=20°.故选 B.
方法归纳
解决“拐点”问题的方法:先过“拐点”作平行线,将一个角分成两个角,再运用平行线的性质解决问题.
3.答案 56
解析 ∵ ∠2=56°,CA 平分∠BCD,∴∠BCD=2∠2=112°.
∵∠D=68°.∴∠D+∠BCD=180°∴AD∥BC,∴∠1=∠2=56°.
4.答案 55
解析 ∵∠1=∠2=70°,∴AB∥CD,∠BGH=180°-∠1=110°.
∵ GM平分∠55°,
∵AB∥CD,∴∠3=∠BGM=55°.
5. 证明 ∵AE平分∠BAD,∴∠1=∠3.
∵AB∥CD,∴∠1=∠2,∴∠2=∠3,
∵∠2=∠AEB,∴∠AEB=∠3,∴AH∥BG,∴∠H+∠G=180°.
能力提升全练
6.C 如图,作BG∥AE,
∵AB⊥AE,∴AB⊥BG,∴∠ABG=90°,∴ ∠ABC=∠ABG+∠CBG=90°+∠CBG.
∵CD∥AE,BG∥AE,∴CD∥BG,∴∠BCD+∠GBC=180°,
∴∠ABC+∠BCD=90°+∠GBC+∠BCD=90°+180°=270°.故选 C.
7.C 如图,作PD∥AB,
由题意,得AB∥CF,∴PD∥AB∥CF,
∵ ∠2=30°,∴∠DPO=∠2=30°.
∵ ∠3=55°,∴ ∠BPO=∠3=55°,∴ ∠BPD =∠BPO-∠DPO=55°-30°= 25°,∴ ∠1=180°-∠BPD=180°-25°=155°.故选 C.
8.解析 BF⊥AC.理由如下:
∵∠AGF=∠ABC,∴BC∥GF,..∠1=∠3.
又∵∠1+∠2=180°,∴ ∠2+∠3=180°,∴ BF∥DE.
∵ DE⊥AC,∴ BF⊥AC.
9.解析 如图,过D作DK∥AB,
∵GH∥AB,EF∥AB,∴GH∥EF∥KD,
∴∠H+∠HDK=180°,∠F+∠FDK=180°.
∵∠F=150°,∴∠FDK=30°
∵∠FDH=∠CDB=35°,∴∠HDK=∠FDH+∠FDK=65°,
∴∠H=115°.
素养探究全练
10.解析 (1)平行.理由如下:
∵AD∥BC,∴∠A+∠B=180°.
又∵∠B=∠D,∴∠D+∠A=180°,∴AB∥CD.
(2)∵AD∥BC,∠B=120°,∴∠DAB=60°.
∵AC平分∠BAE,AF平分∠DAE,
(3)①如图,当点 E 在线段 CD 上时,
∵AB∥CD,∴∠ACD=∠BAC,∠AED=∠BAE,
又∵ ∴ ∠ACD: ∠AED=2:3.
②如图,当点 E在 DC 的延长线上时,
∵AB∥CD,∴∠ACD=∠BAC,∠AED=∠BAE,
又∵ ∴∠ACD:∠AED=2:1.
③当点 E 在 CD的延长线上时, 不成立,不合题意.
综上,∠ACD:∠AED的值为 或2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章 相交线与平行线
3 平行线的性质
第2课时 平行线的性质与判定
基础过关全练
知识点2 平行线的性质与判定
1.如图,已知∠1=40°,∠2= 40°, ∠3 = 140°, 则 ∠4 的度数等于 ( )
A.40° B.36° C.44° D.100°
2.如图所示的是某机械加工厂加工的一种零件的示意图,其中AB∥CD,DE⊥BC,∠ABC=70°,则∠EDC 等于 ( )
A.10° B.20° C.30° D.40°
3.如图, 已 知 ∠2 = 56°, CA 平分∠BCD,∠D=68°,则∠1= °.
4.如图,直线 EF 分别与直线AB,CD 相交于点 G,H,已知∠1=∠2=70°,GM 平分∠HGB 交直线 CD 于点 M,则∠3= °.
5.已知:如图,AB∥CD,AE平分∠BAD,CD 与 AE 相交于 F,∠2=∠AEB.试说明: ∠G+∠H=180°.
能力提升全练
6.情境题·现实生活 小林乘车进入车库时仔细观察了车库门口的曲臂直杆道闸,并抽象出如图所示的模型,已知AB垂直于水平地面AE.当车牌被自动识别后,曲臂直杆道闸的BC段绕点B 缓慢向上旋转,CD 段则一直保持水平状态上升(即CD 与 AE 始终平行),在该过程中∠ABC+∠BCD 始终等于 ( )
A.180° B.250° C.270° D.360°
7.跨物理,凸透镜 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心0的光线相交于点 P,点 F为焦点.若∠2=30°,∠3=55°,则∠1 的度数为 ( )
A.145° B.150° C.135° D.160°
8.如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断 BF 与AC的位置关系,并说明理由.
9.如图,放置在水平操场上的篮球架的横梁 EF 始终平行于AB,主柱AD垂直于地面,EF 与上拉杆 CF 形成的角为∠F,且∠F=150°,可以通过调整 CF和后拉杆BC的位置来调整篮筐的高度,若通过调整使 EF 上升到 GH 的位置,且 GH∥AB,∠CDB=35°,点 H,D,B在同一直线上,求∠H的度数.
素养探究全练
10.如图①,已知AD∥BC(AB>AD),∠B=∠D=120°.
(1)AB与CD平行吗 为什么
(2)若点E,F在线段 CD上,且满足AC平分∠BAE,AF 平分∠DAE,如图②,求∠FAC的度数.
(3)若点 E 在直线 CD 上,且满足∠EAC= 求∠ACD: ∠AED 的值(请自己画出正确图形,并解答).
参考答案
基础过关全练
1.A ∵∠1=40°,∠2=40°,∴∠1=∠2,∴PQ∥MN,∴ ∠3+∠4=180°.
∵∠3=140°,∴∠4=40°.故选 A.
2.B 如图,作EF∥AB,
∵AB∥CD,∴EF∥AB∥CD.
∵∠ABC=70°,∴ ∠BEF=∠ABC=70°.
∵ DE⊥BC,∴∠BED=90°,∴∠FED=90°-70°=20°,
∵ EF∥CD,.∠EDC=∠FED=20°.故选 B.
方法归纳
解决“拐点”问题的方法:先过“拐点”作平行线,将一个角分成两个角,再运用平行线的性质解决问题.
3.答案 56
解析 ∵ ∠2=56°,CA 平分∠BCD,∴∠BCD=2∠2=112°.
∵∠D=68°.∴∠D+∠BCD=180°∴AD∥BC,∴∠1=∠2=56°.
4.答案 55
解析 ∵∠1=∠2=70°,∴AB∥CD,∠BGH=180°-∠1=110°.
∵ GM平分∠55°,
∵AB∥CD,∴∠3=∠BGM=55°.
5. 证明 ∵AE平分∠BAD,∴∠1=∠3.
∵AB∥CD,∴∠1=∠2,∴∠2=∠3,
∵∠2=∠AEB,∴∠AEB=∠3,∴AH∥BG,∴∠H+∠G=180°.
能力提升全练
6.C 如图,作BG∥AE,
∵AB⊥AE,∴AB⊥BG,∴∠ABG=90°,∴ ∠ABC=∠ABG+∠CBG=90°+∠CBG.
∵CD∥AE,BG∥AE,∴CD∥BG,∴∠BCD+∠GBC=180°,
∴∠ABC+∠BCD=90°+∠GBC+∠BCD=90°+180°=270°.故选 C.
7.C 如图,作PD∥AB,
由题意,得AB∥CF,∴PD∥AB∥CF,
∵ ∠2=30°,∴∠DPO=∠2=30°.
∵ ∠3=55°,∴ ∠BPO=∠3=55°,∴ ∠BPD =∠BPO-∠DPO=55°-30°= 25°,∴ ∠1=180°-∠BPD=180°-25°=155°.故选 C.
8.解析 BF⊥AC.理由如下:
∵∠AGF=∠ABC,∴BC∥GF,..∠1=∠3.
又∵∠1+∠2=180°,∴ ∠2+∠3=180°,∴ BF∥DE.
∵ DE⊥AC,∴ BF⊥AC.
9.解析 如图,过D作DK∥AB,
∵GH∥AB,EF∥AB,∴GH∥EF∥KD,
∴∠H+∠HDK=180°,∠F+∠FDK=180°.
∵∠F=150°,∴∠FDK=30°
∵∠FDH=∠CDB=35°,∴∠HDK=∠FDH+∠FDK=65°,
∴∠H=115°.
素养探究全练
10.解析 (1)平行.理由如下:
∵AD∥BC,∴∠A+∠B=180°.
又∵∠B=∠D,∴∠D+∠A=180°,∴AB∥CD.
(2)∵AD∥BC,∠B=120°,∴∠DAB=60°.
∵AC平分∠BAE,AF平分∠DAE,
(3)①如图,当点 E 在线段 CD 上时,
∵AB∥CD,∴∠ACD=∠BAC,∠AED=∠BAE,
又∵ ∴ ∠ACD: ∠AED=2:3.
②如图,当点 E在 DC 的延长线上时,
∵AB∥CD,∴∠ACD=∠BAC,∠AED=∠BAE,
又∵ ∴∠ACD:∠AED=2:1.
③当点 E 在 CD的延长线上时, 不成立,不合题意.
综上,∠ACD:∠AED的值为 或2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
