第七章 相交线与平行线 专项训练 平行线中的四种拐点模型 同步练习(含答案)
文档属性
| 名称 | 第七章 相交线与平行线 专项训练 平行线中的四种拐点模型 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 410.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第七章 相交线与平行线
专项训练 平行线中的四种拐点模型
模型一 铅笔模型
模型解读
【模型】
【条件】AB∥CD.
【结论】∠B+∠D+∠E=360°.
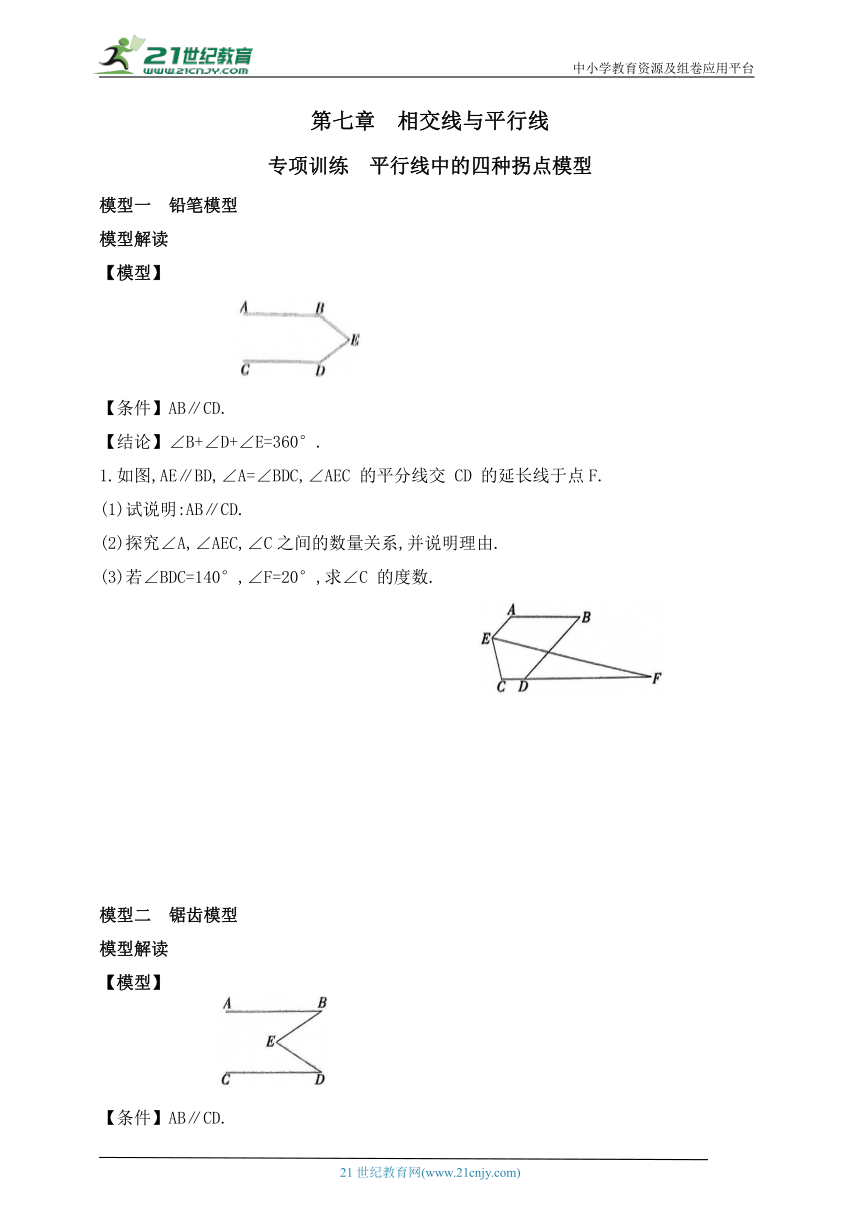
1.如图,AE∥BD,∠A=∠BDC,∠AEC 的平分线交 CD 的延长线于点F.
(1)试说明:AB∥CD.
(2)探究∠A,∠AEC,∠C之间的数量关系,并说明理由.
(3)若∠BDC=140°,∠F=20°,求∠C 的度数.
模型二 锯齿模型
模型解读
【模型】
【条件】AB∥CD.
【结论】∠E=∠B+∠D.
2.(1)如图1,若HD∥GE,∠HAB=50°,∠BCG=20°,求∠ABC的度数.
(2)如图1,点A是直线HD上一点,C 是直线GE上一点,B是直线HD,GE之间的一点, ∠HAB+∠BCG=∠ABC,试说明:AD∥CE.
(3)如图2,在(2)的条件下,作∠BCF=∠BCG,CF与∠BAH的平分线交于点F.若α+β=40°,求∠B+∠F的度数.
模型三 鹰嘴模型
模型解读
【模型】
【条件】AB∥CD.
【结论】∠B=∠D+∠E.
3.问题探究:
(1)如图 1,AB∥CD,点 P 在直线 AB 上方(∠AEP>∠CFP).
①请在拐点 P 处作直线AB 的平行线;
②探究∠AEP,∠CFP,∠EPF 之间的数量关系.
问题拓展:
(2)如图2,AB∥CD,点 P 在直线 AB 上方,∠AEP 的平分线 EM 所在的直线和∠DFP的平分线 FN所在的直线交于点 G(点G在直线 CD的下方),请写出∠EPF 和∠EGF之间的数量关系,并说明理由.
模型四 飞燕模型
模型解读
【模型】
【条件】AB∥CD.
【结论】∠D=∠B+∠E.
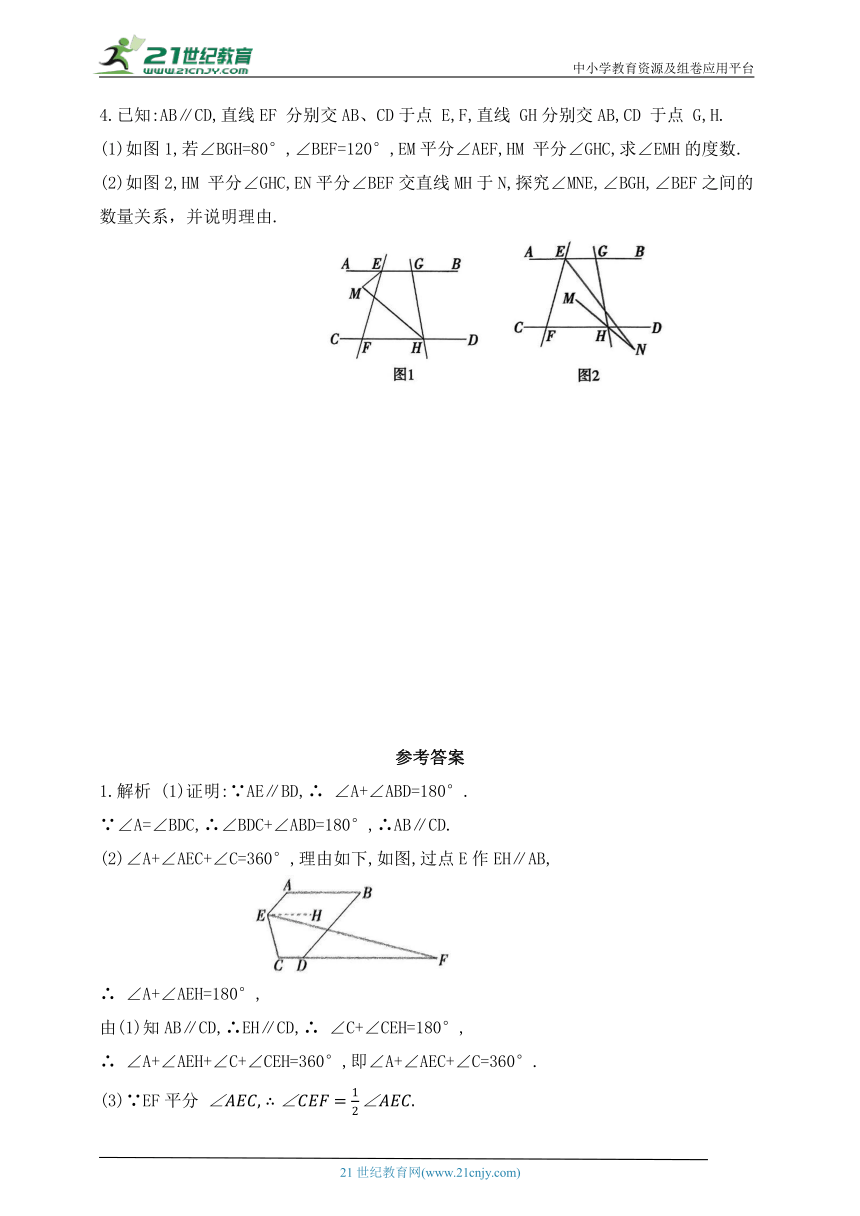
4.已知:AB∥CD,直线EF 分别交AB、CD于点 E,F,直线 GH分别交AB,CD 于点 G,H.
(1)如图1,若∠BGH=80°,∠BEF=120°,EM平分∠AEF,HM 平分∠GHC,求∠EMH的度数.
(2)如图2,HM 平分∠GHC,EN平分∠BEF交直线MH于N,探究∠MNE,∠BGH,∠BEF之间的数量关系,并说明理由.
参考答案
1.解析 (1)证明:∵AE∥BD,∴ ∠A+∠ABD=180°.
∵∠A=∠BDC,∴∠BDC+∠ABD=180°,∴AB∥CD.
(2)∠A+∠AEC+∠C=360°,理由如下,如图,过点E作EH∥AB,
∴ ∠A+∠AEH=180°,
由(1)知AB∥CD,∴EH∥CD,∴ ∠C+∠CEH=180°,
∴ ∠A+∠AEH+∠C+∠CEH=360°,即∠A+∠AEC+∠C=360°.
(3)∵EF平分
在△CEF中,∠F+∠CEF+∠C=180°,
∵ ∠A=∠BDC,∠BDC=140°,∴∠A=140°.
由(2)知∠A+∠AEC+∠C=360°,∴ ∠AEC+∠C=220°②.
②-①,得∠AEC=120°,∴∠C=100°.
2.解析 (1)如图,过点 B作MN∥HD,
∵HD∥GE,∴MN∥HD∥GE,∴∠ABN=∠HAB=50°,∠GCB=∠CBN=20°,
∴ ∠ABC=∠ABN+∠CBN=50°+20°=70°.
(2)证明:如图,过点 B作BP∥HD,
∴∠ABP=∠HAB,
∵∠ABC=∠ABP+∠CBP,∠ABC=∠HAB+∠BCG,∴∠CBP=∠BCG,∴BP∥GE,
∴ AD∥CE.
(3)∵AF平分∠HAB,∴∠HAF=∠FAB=β,∴∠HAB=2∠FAB=2β.
∵∠BCF=∠BCG=α,∴∠FCG=2∠FCB=2α.
∵∠B=∠HAB+∠BCG,且由AD∥CE可知∠F=∠HAF+∠FCG,
∴∴∠B+∠F的度数为120°.
3.解析 (1)①如图,直线ST即为过点 P 且平行于直线AB 的直线.
②∵ST∥AB,AB∥CD,∴ST∥AB∥CD,∴∠AEP=∠TPE,∠CFP=∠TPF,
∴∠AEP=∠TPE=∠TPF+∠EPF=∠CFP+∠EPF,即∠AEP=∠CFP+∠EPF.
(2)如图,设GM与 CD交于点 H,
设∠AEM=x,∠DFN=y,
∵EM平分∠AEP,FN平分∠DFP,∴∠AEP=2x,∠PFD=2y,
由(1)得∠P=∠AEP-∠CFP
即
∵AB∥CD,∴∠CHM=∠AEM=x,
∵∠CHM=∠GHF=x,∠HFG=∠NFD=y,
即∠EPF+2∠EGF=180°.
4.解析 (1)如图,过M作MN∥AB.
∵AB∥CD,∴MN∥CD,∠BGH=∠GHC=80°.
∵ HM平分
∵ ∠BEF=120°,∴ ∠AEF=60°.
∵EM平分
∵MN∥AB∥CD,∴∠EMN=∠AEM=30°,∠HMN=∠MHC=40°,
∴ ∠EMH=∠EMN+∠HMN=30°+40°=70°.
理由如下:如图,过点 N作NK∥CD.
∵AB∥CD,∴NK∥AB,∴∠ENK=∠BEN.
∵EN平分∠
∵NK∥CD,∴∠MHC=∠MNK.
∵ HM 平分
∵AB∥CD,∴∠BGH=∠GHC,
∵∠MNE=∠ENK-∠MNK,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章 相交线与平行线
专项训练 平行线中的四种拐点模型
模型一 铅笔模型
模型解读
【模型】
【条件】AB∥CD.
【结论】∠B+∠D+∠E=360°.
1.如图,AE∥BD,∠A=∠BDC,∠AEC 的平分线交 CD 的延长线于点F.
(1)试说明:AB∥CD.
(2)探究∠A,∠AEC,∠C之间的数量关系,并说明理由.
(3)若∠BDC=140°,∠F=20°,求∠C 的度数.
模型二 锯齿模型
模型解读
【模型】
【条件】AB∥CD.
【结论】∠E=∠B+∠D.
2.(1)如图1,若HD∥GE,∠HAB=50°,∠BCG=20°,求∠ABC的度数.
(2)如图1,点A是直线HD上一点,C 是直线GE上一点,B是直线HD,GE之间的一点, ∠HAB+∠BCG=∠ABC,试说明:AD∥CE.
(3)如图2,在(2)的条件下,作∠BCF=∠BCG,CF与∠BAH的平分线交于点F.若α+β=40°,求∠B+∠F的度数.
模型三 鹰嘴模型
模型解读
【模型】
【条件】AB∥CD.
【结论】∠B=∠D+∠E.
3.问题探究:
(1)如图 1,AB∥CD,点 P 在直线 AB 上方(∠AEP>∠CFP).
①请在拐点 P 处作直线AB 的平行线;
②探究∠AEP,∠CFP,∠EPF 之间的数量关系.
问题拓展:
(2)如图2,AB∥CD,点 P 在直线 AB 上方,∠AEP 的平分线 EM 所在的直线和∠DFP的平分线 FN所在的直线交于点 G(点G在直线 CD的下方),请写出∠EPF 和∠EGF之间的数量关系,并说明理由.
模型四 飞燕模型
模型解读
【模型】
【条件】AB∥CD.
【结论】∠D=∠B+∠E.
4.已知:AB∥CD,直线EF 分别交AB、CD于点 E,F,直线 GH分别交AB,CD 于点 G,H.
(1)如图1,若∠BGH=80°,∠BEF=120°,EM平分∠AEF,HM 平分∠GHC,求∠EMH的度数.
(2)如图2,HM 平分∠GHC,EN平分∠BEF交直线MH于N,探究∠MNE,∠BGH,∠BEF之间的数量关系,并说明理由.
参考答案
1.解析 (1)证明:∵AE∥BD,∴ ∠A+∠ABD=180°.
∵∠A=∠BDC,∴∠BDC+∠ABD=180°,∴AB∥CD.
(2)∠A+∠AEC+∠C=360°,理由如下,如图,过点E作EH∥AB,
∴ ∠A+∠AEH=180°,
由(1)知AB∥CD,∴EH∥CD,∴ ∠C+∠CEH=180°,
∴ ∠A+∠AEH+∠C+∠CEH=360°,即∠A+∠AEC+∠C=360°.
(3)∵EF平分
在△CEF中,∠F+∠CEF+∠C=180°,
∵ ∠A=∠BDC,∠BDC=140°,∴∠A=140°.
由(2)知∠A+∠AEC+∠C=360°,∴ ∠AEC+∠C=220°②.
②-①,得∠AEC=120°,∴∠C=100°.
2.解析 (1)如图,过点 B作MN∥HD,
∵HD∥GE,∴MN∥HD∥GE,∴∠ABN=∠HAB=50°,∠GCB=∠CBN=20°,
∴ ∠ABC=∠ABN+∠CBN=50°+20°=70°.
(2)证明:如图,过点 B作BP∥HD,
∴∠ABP=∠HAB,
∵∠ABC=∠ABP+∠CBP,∠ABC=∠HAB+∠BCG,∴∠CBP=∠BCG,∴BP∥GE,
∴ AD∥CE.
(3)∵AF平分∠HAB,∴∠HAF=∠FAB=β,∴∠HAB=2∠FAB=2β.
∵∠BCF=∠BCG=α,∴∠FCG=2∠FCB=2α.
∵∠B=∠HAB+∠BCG,且由AD∥CE可知∠F=∠HAF+∠FCG,
∴∴∠B+∠F的度数为120°.
3.解析 (1)①如图,直线ST即为过点 P 且平行于直线AB 的直线.
②∵ST∥AB,AB∥CD,∴ST∥AB∥CD,∴∠AEP=∠TPE,∠CFP=∠TPF,
∴∠AEP=∠TPE=∠TPF+∠EPF=∠CFP+∠EPF,即∠AEP=∠CFP+∠EPF.
(2)如图,设GM与 CD交于点 H,
设∠AEM=x,∠DFN=y,
∵EM平分∠AEP,FN平分∠DFP,∴∠AEP=2x,∠PFD=2y,
由(1)得∠P=∠AEP-∠CFP
即
∵AB∥CD,∴∠CHM=∠AEM=x,
∵∠CHM=∠GHF=x,∠HFG=∠NFD=y,
即∠EPF+2∠EGF=180°.
4.解析 (1)如图,过M作MN∥AB.
∵AB∥CD,∴MN∥CD,∠BGH=∠GHC=80°.
∵ HM平分
∵ ∠BEF=120°,∴ ∠AEF=60°.
∵EM平分
∵MN∥AB∥CD,∴∠EMN=∠AEM=30°,∠HMN=∠MHC=40°,
∴ ∠EMH=∠EMN+∠HMN=30°+40°=70°.
理由如下:如图,过点 N作NK∥CD.
∵AB∥CD,∴NK∥AB,∴∠ENK=∠BEN.
∵EN平分∠
∵NK∥CD,∴∠MHC=∠MNK.
∵ HM 平分
∵AB∥CD,∴∠BGH=∠GHC,
∵∠MNE=∠ENK-∠MNK,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
