第七章《相交线与平行线》素养综合检测(含答案)
文档属性
| 名称 | 第七章《相交线与平行线》素养综合检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 532.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 14:37:50 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第七章素养综合检测
时间:60分钟 满分:100分
一、选择题(每小题3分,共30分)
1.下列四个图形中,∠1和∠2互为对顶角的是 ( )
2.小布家通往滨河大道有 4 条路线(如图),长度分别约为700m,900 m,2 000 m和2 500 m,根据图形可以判定路线②的长度约为 ( )
A.2500 m B.2000 m C.900 m D.700 m
第2题图 第3题图
3.如图所示的是一个可折叠晾衣架的侧面示意图,AB 表示地面,当PM∥AB,PN∥AB时,就可以确定点N,P,M在同一直线上,这样判定的依据是 ( )
A.过直线外一点,有且只有一条直线与这条直线平行
B.内错角相等,两直线平行
C.两点确定一条直线
D.平行于同一直线的两直线平行
4.如图,是 与 的截线.找出∠1的同位角,标为∠2,找出∠1 的同旁内角,标为∠3.下列选项中为∠1,∠2,∠3正确的位置图的是( )
5.两直线相交形成的4个角的度数之比依次可能是 ( )
A.2:3:2:3 B.1:1:4:4 C.1:2:3:4 D.3:4:4:3
6.下列说法中,正确的是 ( )
A.一个角的补角一定大于这个角
B.任何一个角都有补角
C.若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余
D.一个角如果有余角,那么这个角的补角与它的余角的差为90°
7.如图,点 O 在直线AB上,OC⊥OD.若∠BOC=130°,则∠AOD 的度数为 ( )
A.20° B.30° C.40° D.50°
8.如图,直线AB,CD相交于点E,EF⊥AB于E,若∠CEF=65°,则∠DEB的度数为( )
A.155° B.135° C.35° D.25°
9.跨物理·光的折射 当光线从空气射入水中时,光线的传播方向发生了改变,这就是光的折射现象(如图所示),∠1=80°,∠2=40°,则∠3 的度数为 ( )
A.30° B.40° C.50° D.70°
10.一种路灯的示意图如图所示,其底部支架 AB 与吊线 FG平行,灯杆 CD 与底部支架AB 所成锐角α=15°.顶部支架EF 与灯杆 CD 所成锐角β=45°,则 EF 与 FG 所成锐角的度数为( )
A.60° B.55° C.50° D.45°
二、填空题(每小题3分,共18分)
11.若α与β互为补角,α=33°27',则β= .
12.如图所示的是一把剪子,若∠AOB+∠COD=32°,则∠BOD= .
13.如图,直线AB,CD 相交于点O,EO⊥CD 于点 O.若∠AOC:∠BOE=2:3,则∠AOE= °.
14.如图,给出条件:①∠C=∠BDE;②∠C=∠CAF;③∠B+∠EDG=180°;④∠BAC+∠C=180°.其中能判定 AB∥CD 的是 .(注:填上所有符合条件的序号)
15.情境题·现实生活 消防云梯的示意图如图1所示,其由救援台AB、延展臂BC(B在 C 的左侧)、伸展主臂 CD、支撑臂EF 构成,在作业过程中,救援台 AB、车身GH及地面 MN三者始终保持平行.为了参与一项高空救援工作,需要进行作业调整,如图2,使得延展臂 BC 与支撑臂 EF 所在直线互相垂直,且∠EFH=69°,则此时∠ABC= .
16.将一副三角尺中的两块直角三角尺的直角顶点按如图所示的方式叠放在一起,其中∠A=60°,∠D=30°,∠E=∠B=45°.当∠ACE<90°,且点 E 在直线AC 的上方时,若这两块直角三角尺有两条边平行,则∠ACE= .
三、解答题(共52分)
17.(4分)若一个角的补角比它的余角的3倍多14°,求这个角的度数.
18.(8分)已知∠α和∠β(如图),求作∠BAC,使∠BAC=∠α+∠β;再在∠BAC 的一边上取一点 D,过这一点作另一边的平行线DG.(用尺规作图,不写作法,保留作图痕迹)
19.(8分)如图所示的是一条小鱼的简笔画,∠B=50°,∠BDC=50°,∠A=∠1,∠ACD+∠DFH=180°,试说明:AB∥FH.
20.(10 分)如图,直线AB,CD 相交于点 O,∠AOC=70°,射线 OE 把∠BOD 分成两个角,且∠BOE : ∠EOD =3:4.
(1)求∠EOD 的度数.
(2)过点O 作射线OF⊥OE,求∠DOF 的度数.
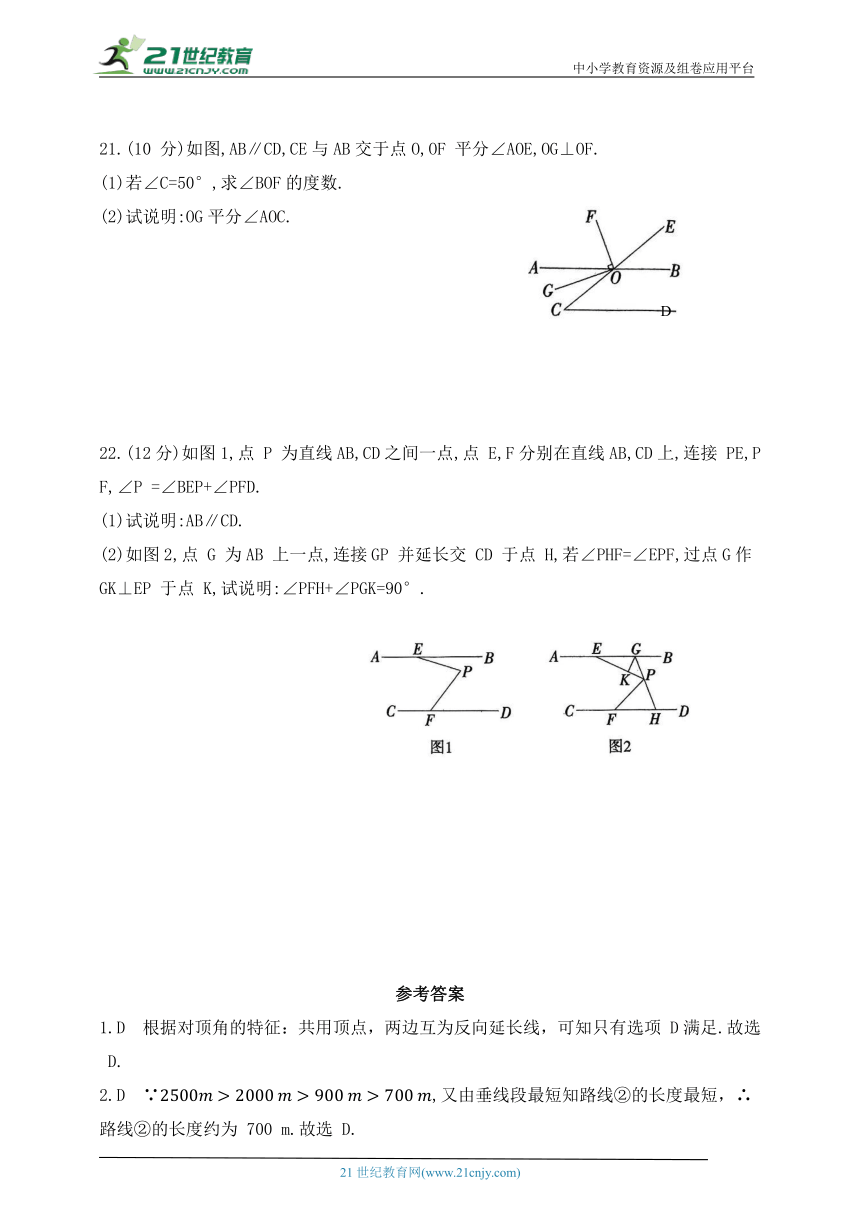
21.(10 分)如图,AB∥CD,CE与AB交于点O,OF 平分∠AOE,OG⊥OF.
(1)若∠C=50°,求∠BOF的度数.
(2)试说明:OG平分∠AOC.
22.(12分)如图1,点 P 为直线AB,CD之间一点,点 E,F分别在直线AB,CD上,连接 PE,PF,∠P =∠BEP+∠PFD.
(1)试说明:AB∥CD.
(2)如图2,点 G 为AB 上一点,连接GP 并延长交 CD 于点 H,若∠PHF=∠EPF,过点G作 GK⊥EP 于点 K,试说明:∠PFH+∠PGK=90°.
参考答案
1.D 根据对顶角的特征:共用顶点,两边互为反向延长线,可知只有选项 D满足.故选 D.
2.D ∵,又由垂线段最短知路线②的长度最短,∴路线②的长度约为 700 m.故选 D.
3.A PM,PN都过点 P,当PM∥AB,PN∥AB时,确定点N,P,M在同一直线上的依据是过直线外一点,有且只有一条直线与这条直线平行.故选 A.
4.C 同位角位于截线的同侧,被截直线的同侧,同旁内角位于截线的同侧,被截直线之间.故选 C.
5.A 两直线相交形成的4个角中有2对对顶角,4对邻补角,对顶角相等,邻补角互补.选项中符合的为A.
6.D A.90°角的补角等于90°,故该选项错误;
B.180°角没有补角,故该选项错误;
C.因为∠1,∠2,∠3是3个角,所以不能说∠1,∠2,∠3互余,故该选项错误;
D.设这个角为α,则这个角的补角为180°-α,余角为 所以这个角的补角与它的余角的差为90°,该选项正确.故选 D.
7.C ∵∠BOC=130°,.. ∠AOC=180°-∠BOC=50°.∵OC⊥OD,∴∠COD=90°,∴∠AOD=90°-∠AOC=40°.故选 C.
8.D ∵EF⊥AB于E,∠CEF=65°,∴∠BED=∠AEC= .故选 D.
9.B 如图,∵ AB∥CD,∴ ∠1=∠AMN=∠2+∠3.
∵∠1=80°,∠2=40°,∴∠3=40°.故选 B.
10.A 如图,过点E作EH∥AB,
∵AB∥FG,∴ AB∥EH∥FG,∴∠BEH=α=15°,∠FEH+∠EFG=180°.
∵β=45°,∴∠FEH=180°-45°-15°=120°,
∴∠EFG=180°-∠FEH=180°-120°=60°,
∴EF 与 FG 所成锐角的度数为 60°.故选 A.
11.答案 146°33'
解析 ∵α与β互为补角,α=33°27',∴β=180°-
12.答案 164°
解析 ∠AOB=∠COD,且∠AOB+∠COD=32°,∴ ∠AOB=16°,∴∠BOD=180°-∠AOB=164°.
13.答案 126
解析 ∵ EO⊥CD,∴ ∠DOE = ∠COE = 90°,∴∠BOD+ ∠BOE = 90°.
∵ ∠BOD = ∠AOC,∴∠AOC+∠BOE=90°.
∵ ∠AOC :∠BOE=2:3,
14.答案 ②③④
解析 ①∵∠C=∠BDE,∴AC∥BG,故①不符合题意;②∵∠C=∠CAF,∴AB∥CD,故②符合题意;③∵∠B+∠EDG = 180°,∠BDE +∠EDG = 180°,∴∠B = ∠BDE,∴ AB ∥CD,故③符合题意;④∵∠BAC+∠C=180°,∴AB∥CD,故④符合题意.故答案为②③④.
15.答案 159°
解析 如图,延长 BC,FE,相交于点 P,则 BP⊥EP,延长AB交 FE 的延长线于点 Q,作 PK∥AB,
∵ AB ∥FH,∴ PK ∥AB ∥FH.
∵ ∠EFH = 69°,∴∠EPK=∠EFH=69°.
∵ BP⊥EP,∴ ∠BPE=90°,∴∠BPK=90°-69°=21°,∴∠QBC=∠BPK=21°,
∴ ∠ABC=180°-∠QBC=180°-21°=159°.
16.答案 30°或45°
解析 由条件分析可知,仅存在以下两种情况:
①当BE∥AC时,∠ACE=∠E=45°;
②当BC∥AD时,∠D=∠DCB=30°,∴∠DCE=90°-30°=60°,
综上,∠ACE等于30°或45°.
17.解析 设这个角为x°,则其余角为(90-x)°,补角为(180-x)°,
依题意有180-x=3·(90-x)+14,解得x=52.
答:这个角的度数是52°.
18.解析 答案不唯一,如图所示.
19.证明 ∵∠B=50°,∠BDC=50°,∴∠B=∠BDC,∴AB∥CD,∴∠A=∠ACD.
∵∠A=∠1,∴∠ACD=∠1.
∵ ∠ACD+∠DFH=180°,∴ ∠1+∠DFH=180°,∴FH∥CD,∴AB∥FH.
20.解析 (1)∵∠AOC=70°,∴ ∠BOD=∠AOC=70°.
∵∠BOD=∠BOE+∠DOE,∠BOE:∠EOD=3:4,
(2)当OF在OE上方时,如图1,
∵OF⊥OE,∴∠FOE=90°,
∵∠DOE=40°,∴ ∠DOF=∠FOE-∠DOE=90°-40°=50°.
当OF在OE下方时,如图2,
∵OF⊥OE,∴∠FOE=90°.
∵∠EOD=40°,∴ ∠DOF=∠FOE+∠EOD=90°+40°=130°.
综上可知,∠DOF的度数是50°或130°.
21.解析 (1)∵AB∥CD,∴∠BOE=∠C=50°,∴ ∠AOE=130°.
∵OF平分∠AOE,∴∠EOF=∠AOF=65°,
∴∠BOF=∠BOE+∠EOF=50°+65°=115°.
(2)证明:∵OG⊥OF,即∠GOF=90°,
∴∠AOF+∠AOG=90°,∠EOF+∠COG=90°.
∵∠AOF=∠EOF,∴∠AOG=∠COG,∴OG平分∠AOC.
22.证明 (1)如图1,过点 P作PM∥AB,则∠BEP=∠MPE.
∵ ∠EPF = ∠BEP+∠PFD,∴ ∠EPF =∠MPE+∠PFD,∴∠EPF-∠MPE=∠PFD,
∴∠MPF=∠PFD,∴PM∥CD,∴AB∥CD.
(2)如图2,过点P作PM∥CD,∴∠MPG=∠PHF.
∵∠PHF=∠EPF,∴∠MPG=∠EPF,∴∠MPF=∠GPK.
∥
过点 P作 交AB于点 N,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章素养综合检测
时间:60分钟 满分:100分
一、选择题(每小题3分,共30分)
1.下列四个图形中,∠1和∠2互为对顶角的是 ( )
2.小布家通往滨河大道有 4 条路线(如图),长度分别约为700m,900 m,2 000 m和2 500 m,根据图形可以判定路线②的长度约为 ( )
A.2500 m B.2000 m C.900 m D.700 m
第2题图 第3题图
3.如图所示的是一个可折叠晾衣架的侧面示意图,AB 表示地面,当PM∥AB,PN∥AB时,就可以确定点N,P,M在同一直线上,这样判定的依据是 ( )
A.过直线外一点,有且只有一条直线与这条直线平行
B.内错角相等,两直线平行
C.两点确定一条直线
D.平行于同一直线的两直线平行
4.如图,是 与 的截线.找出∠1的同位角,标为∠2,找出∠1 的同旁内角,标为∠3.下列选项中为∠1,∠2,∠3正确的位置图的是( )
5.两直线相交形成的4个角的度数之比依次可能是 ( )
A.2:3:2:3 B.1:1:4:4 C.1:2:3:4 D.3:4:4:3
6.下列说法中,正确的是 ( )
A.一个角的补角一定大于这个角
B.任何一个角都有补角
C.若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余
D.一个角如果有余角,那么这个角的补角与它的余角的差为90°
7.如图,点 O 在直线AB上,OC⊥OD.若∠BOC=130°,则∠AOD 的度数为 ( )
A.20° B.30° C.40° D.50°
8.如图,直线AB,CD相交于点E,EF⊥AB于E,若∠CEF=65°,则∠DEB的度数为( )
A.155° B.135° C.35° D.25°
9.跨物理·光的折射 当光线从空气射入水中时,光线的传播方向发生了改变,这就是光的折射现象(如图所示),∠1=80°,∠2=40°,则∠3 的度数为 ( )
A.30° B.40° C.50° D.70°
10.一种路灯的示意图如图所示,其底部支架 AB 与吊线 FG平行,灯杆 CD 与底部支架AB 所成锐角α=15°.顶部支架EF 与灯杆 CD 所成锐角β=45°,则 EF 与 FG 所成锐角的度数为( )
A.60° B.55° C.50° D.45°
二、填空题(每小题3分,共18分)
11.若α与β互为补角,α=33°27',则β= .
12.如图所示的是一把剪子,若∠AOB+∠COD=32°,则∠BOD= .
13.如图,直线AB,CD 相交于点O,EO⊥CD 于点 O.若∠AOC:∠BOE=2:3,则∠AOE= °.
14.如图,给出条件:①∠C=∠BDE;②∠C=∠CAF;③∠B+∠EDG=180°;④∠BAC+∠C=180°.其中能判定 AB∥CD 的是 .(注:填上所有符合条件的序号)
15.情境题·现实生活 消防云梯的示意图如图1所示,其由救援台AB、延展臂BC(B在 C 的左侧)、伸展主臂 CD、支撑臂EF 构成,在作业过程中,救援台 AB、车身GH及地面 MN三者始终保持平行.为了参与一项高空救援工作,需要进行作业调整,如图2,使得延展臂 BC 与支撑臂 EF 所在直线互相垂直,且∠EFH=69°,则此时∠ABC= .
16.将一副三角尺中的两块直角三角尺的直角顶点按如图所示的方式叠放在一起,其中∠A=60°,∠D=30°,∠E=∠B=45°.当∠ACE<90°,且点 E 在直线AC 的上方时,若这两块直角三角尺有两条边平行,则∠ACE= .
三、解答题(共52分)
17.(4分)若一个角的补角比它的余角的3倍多14°,求这个角的度数.
18.(8分)已知∠α和∠β(如图),求作∠BAC,使∠BAC=∠α+∠β;再在∠BAC 的一边上取一点 D,过这一点作另一边的平行线DG.(用尺规作图,不写作法,保留作图痕迹)
19.(8分)如图所示的是一条小鱼的简笔画,∠B=50°,∠BDC=50°,∠A=∠1,∠ACD+∠DFH=180°,试说明:AB∥FH.
20.(10 分)如图,直线AB,CD 相交于点 O,∠AOC=70°,射线 OE 把∠BOD 分成两个角,且∠BOE : ∠EOD =3:4.
(1)求∠EOD 的度数.
(2)过点O 作射线OF⊥OE,求∠DOF 的度数.
21.(10 分)如图,AB∥CD,CE与AB交于点O,OF 平分∠AOE,OG⊥OF.
(1)若∠C=50°,求∠BOF的度数.
(2)试说明:OG平分∠AOC.
22.(12分)如图1,点 P 为直线AB,CD之间一点,点 E,F分别在直线AB,CD上,连接 PE,PF,∠P =∠BEP+∠PFD.
(1)试说明:AB∥CD.
(2)如图2,点 G 为AB 上一点,连接GP 并延长交 CD 于点 H,若∠PHF=∠EPF,过点G作 GK⊥EP 于点 K,试说明:∠PFH+∠PGK=90°.
参考答案
1.D 根据对顶角的特征:共用顶点,两边互为反向延长线,可知只有选项 D满足.故选 D.
2.D ∵,又由垂线段最短知路线②的长度最短,∴路线②的长度约为 700 m.故选 D.
3.A PM,PN都过点 P,当PM∥AB,PN∥AB时,确定点N,P,M在同一直线上的依据是过直线外一点,有且只有一条直线与这条直线平行.故选 A.
4.C 同位角位于截线的同侧,被截直线的同侧,同旁内角位于截线的同侧,被截直线之间.故选 C.
5.A 两直线相交形成的4个角中有2对对顶角,4对邻补角,对顶角相等,邻补角互补.选项中符合的为A.
6.D A.90°角的补角等于90°,故该选项错误;
B.180°角没有补角,故该选项错误;
C.因为∠1,∠2,∠3是3个角,所以不能说∠1,∠2,∠3互余,故该选项错误;
D.设这个角为α,则这个角的补角为180°-α,余角为 所以这个角的补角与它的余角的差为90°,该选项正确.故选 D.
7.C ∵∠BOC=130°,.. ∠AOC=180°-∠BOC=50°.∵OC⊥OD,∴∠COD=90°,∴∠AOD=90°-∠AOC=40°.故选 C.
8.D ∵EF⊥AB于E,∠CEF=65°,∴∠BED=∠AEC= .故选 D.
9.B 如图,∵ AB∥CD,∴ ∠1=∠AMN=∠2+∠3.
∵∠1=80°,∠2=40°,∴∠3=40°.故选 B.
10.A 如图,过点E作EH∥AB,
∵AB∥FG,∴ AB∥EH∥FG,∴∠BEH=α=15°,∠FEH+∠EFG=180°.
∵β=45°,∴∠FEH=180°-45°-15°=120°,
∴∠EFG=180°-∠FEH=180°-120°=60°,
∴EF 与 FG 所成锐角的度数为 60°.故选 A.
11.答案 146°33'
解析 ∵α与β互为补角,α=33°27',∴β=180°-
12.答案 164°
解析 ∠AOB=∠COD,且∠AOB+∠COD=32°,∴ ∠AOB=16°,∴∠BOD=180°-∠AOB=164°.
13.答案 126
解析 ∵ EO⊥CD,∴ ∠DOE = ∠COE = 90°,∴∠BOD+ ∠BOE = 90°.
∵ ∠BOD = ∠AOC,∴∠AOC+∠BOE=90°.
∵ ∠AOC :∠BOE=2:3,
14.答案 ②③④
解析 ①∵∠C=∠BDE,∴AC∥BG,故①不符合题意;②∵∠C=∠CAF,∴AB∥CD,故②符合题意;③∵∠B+∠EDG = 180°,∠BDE +∠EDG = 180°,∴∠B = ∠BDE,∴ AB ∥CD,故③符合题意;④∵∠BAC+∠C=180°,∴AB∥CD,故④符合题意.故答案为②③④.
15.答案 159°
解析 如图,延长 BC,FE,相交于点 P,则 BP⊥EP,延长AB交 FE 的延长线于点 Q,作 PK∥AB,
∵ AB ∥FH,∴ PK ∥AB ∥FH.
∵ ∠EFH = 69°,∴∠EPK=∠EFH=69°.
∵ BP⊥EP,∴ ∠BPE=90°,∴∠BPK=90°-69°=21°,∴∠QBC=∠BPK=21°,
∴ ∠ABC=180°-∠QBC=180°-21°=159°.
16.答案 30°或45°
解析 由条件分析可知,仅存在以下两种情况:
①当BE∥AC时,∠ACE=∠E=45°;
②当BC∥AD时,∠D=∠DCB=30°,∴∠DCE=90°-30°=60°,
综上,∠ACE等于30°或45°.
17.解析 设这个角为x°,则其余角为(90-x)°,补角为(180-x)°,
依题意有180-x=3·(90-x)+14,解得x=52.
答:这个角的度数是52°.
18.解析 答案不唯一,如图所示.
19.证明 ∵∠B=50°,∠BDC=50°,∴∠B=∠BDC,∴AB∥CD,∴∠A=∠ACD.
∵∠A=∠1,∴∠ACD=∠1.
∵ ∠ACD+∠DFH=180°,∴ ∠1+∠DFH=180°,∴FH∥CD,∴AB∥FH.
20.解析 (1)∵∠AOC=70°,∴ ∠BOD=∠AOC=70°.
∵∠BOD=∠BOE+∠DOE,∠BOE:∠EOD=3:4,
(2)当OF在OE上方时,如图1,
∵OF⊥OE,∴∠FOE=90°,
∵∠DOE=40°,∴ ∠DOF=∠FOE-∠DOE=90°-40°=50°.
当OF在OE下方时,如图2,
∵OF⊥OE,∴∠FOE=90°.
∵∠EOD=40°,∴ ∠DOF=∠FOE+∠EOD=90°+40°=130°.
综上可知,∠DOF的度数是50°或130°.
21.解析 (1)∵AB∥CD,∴∠BOE=∠C=50°,∴ ∠AOE=130°.
∵OF平分∠AOE,∴∠EOF=∠AOF=65°,
∴∠BOF=∠BOE+∠EOF=50°+65°=115°.
(2)证明:∵OG⊥OF,即∠GOF=90°,
∴∠AOF+∠AOG=90°,∠EOF+∠COG=90°.
∵∠AOF=∠EOF,∴∠AOG=∠COG,∴OG平分∠AOC.
22.证明 (1)如图1,过点 P作PM∥AB,则∠BEP=∠MPE.
∵ ∠EPF = ∠BEP+∠PFD,∴ ∠EPF =∠MPE+∠PFD,∴∠EPF-∠MPE=∠PFD,
∴∠MPF=∠PFD,∴PM∥CD,∴AB∥CD.
(2)如图2,过点P作PM∥CD,∴∠MPG=∠PHF.
∵∠PHF=∠EPF,∴∠MPG=∠EPF,∴∠MPF=∠GPK.
∥
过点 P作 交AB于点 N,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
