2025年中考数学九年级一轮复习【图形的变化】专题(平面向量部分)过关题(含答案)
文档属性
| 名称 | 2025年中考数学九年级一轮复习【图形的变化】专题(平面向量部分)过关题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 134.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 17:04:29 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年中考数学九年级一轮复习【图形的变化】专题(平面向量)部分过关题
一、单选题
1.(2018九上·金山期末)如图,梯形ABCD中,AD∥BC,AB=DC,DE∥AB,下列各式正确的是( )
A. ; B. ;
C. ; D. .
2.(2023九上·浦东期中)对于非零向量、、,下列条件中,不能判定与是平行向量的是( )
A., B.,
C. D.
3.(2018·黄浦模拟)计算: ( )
A. ; B. ; C. ; D.0.
4.(2024九上·嘉定月考)下列说法中,正确的是( )
A.如果和是相反向量,那么
B.如果和是平行向量,那么
C.如果,那么
D.如果,那么
5.(2021九上·松江期末)已知=2,那么下列判断错误的是( )
A.﹣2=0 B.
C.||=2|| D.
6.(2024九上·浦东期中)下列关于空间向量的命题中,正确命题的个数是( )
①任一向量与它的相反向量都不相等;
②长度相等、方向相同的两个向量是相等向量;
③平行且模相等的两个向量是相等向量;
④若a≠b,则|a|≠|b|;
⑤两个向量相等,则它们的起点与终点相同.
A.0 B.1 C.2 D.3
7.(2019·顺义模拟)规定:在平面直角坐标系xOy中,如果点P的坐标为(m,n),向量 可以用点P的坐标表示为: =(m,n).已知 =(x1,y1), =(x2,y2),如果x1x2+y1y2=0,那么 与 互相垂直.下列四组向量中,互相垂直的是( )
A. , B. ,
C. , D. ,
8.(2017·普陀模拟)如图,在△ABC中,中线AD、CE交于点O,设 = , = ,那么向量 用向量 、 表示为( )
A.+ B.+
C.+ D.+
9.(2024九上·崇明期中)下列说法中,正确的是( )
A.
B.如果,那么
C.如果是单位向量,那么
D.如果是非零向量,且,那么
二、填空题
10.(2023九上·闵行期中)过的重心作,分别交于点,于点,如果,那么 .
11.(2024九上·上海市月考)已知与单位向量的方向相反,且长度为4,那么表示为
12.(2024九下·上海市模拟)如图,已知在中,点D是边的中点,设,,用向量、表示向量 ,
13.(2016九上·浦东期中)如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB, ,那么 = .
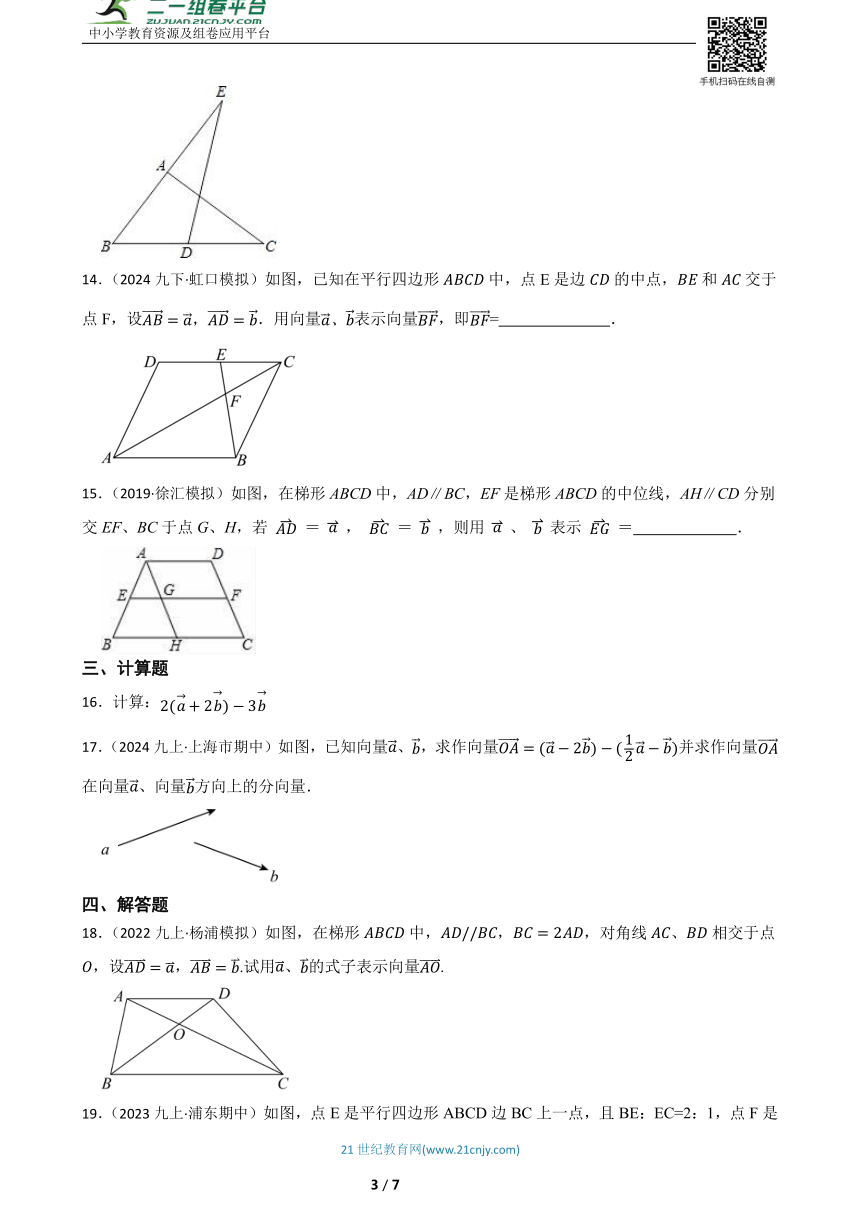
14.(2024九下·虹口模拟)如图,已知在平行四边形中,点E是边的中点,和交于点F,设.用向量表示向量,即= .
15.(2019·徐汇模拟)如图,在梯形ABCD中,AD∥BC,EF是梯形ABCD的中位线,AH∥CD分别交EF、BC于点G、H,若 = , = ,则用 、 表示 = .
三、计算题
16.计算:
17.(2024九上·上海市期中)如图,已知向量、,求作向量并求作向量在向量、向量方向上的分向量.
四、解答题
18.(2022九上·杨浦模拟)如图,在梯形中,,,对角线、相交于点,设,.试用、的式子表示向量.
19.(2023九上·浦东期中)如图,点E是平行四边形ABCD边BC上一点,且BE:EC=2:1,点F是边CD的中点,AE与BF交于点O.
(1)设=,=,试用、表示;
(2)求BO:OF的值.
答案解析部分
1.【答案】D
【知识点】平面向量及其表示
2.【答案】D
【知识点】平行向量定理
3.【答案】C
【知识点】向量的加法法则
4.【答案】D
【知识点】平面向量及其表示
5.【答案】A
【知识点】实数与向量相乘运算法则;平行向量定理
6.【答案】B
【知识点】实数与向量相乘运算法则
7.【答案】B
【知识点】平面向量及其表示;向量的线性运算
8.【答案】B
【知识点】实数与向量相乘运算法则
9.【答案】D
【知识点】平面向量及其表示
10.【答案】
【知识点】向量的线性运算
11.【答案】
【知识点】向量的线性运算
12.【答案】
【知识点】向量的线性运算
13.【答案】2 ﹣
【知识点】向量的加法运算律
14.【答案】
【知识点】向量的线性运算
15.【答案】 .
【知识点】向量的线性运算
16.【答案】原式=
【知识点】向量的加法法则;实数与向量相乘的运算律
17.【答案】解:
,
如图,向量即为所作:
向量即为在向量方向上的分向量,
向量即为在向量方向上的分向量.
【知识点】实数与向量相乘运算法则;向量的线性运算
18.【答案】
【知识点】实数与向量相乘运算法则
19.【答案】(1)解:∵BE:EC=2:1,,
∴,
∴;
(2)解:
过点E作EM∥CD,
则,,
∵点F是CD中点,
∴,
设OM=a,则BO=3a,MF=2a,
故可得.
【知识点】平行向量定理;向量的线性运算
21世纪教育网(www.21cnjy.com)
7 / 7
2025年中考数学九年级一轮复习【图形的变化】专题(平面向量)部分过关题
一、单选题
1.(2018九上·金山期末)如图,梯形ABCD中,AD∥BC,AB=DC,DE∥AB,下列各式正确的是( )
A. ; B. ;
C. ; D. .
2.(2023九上·浦东期中)对于非零向量、、,下列条件中,不能判定与是平行向量的是( )
A., B.,
C. D.
3.(2018·黄浦模拟)计算: ( )
A. ; B. ; C. ; D.0.
4.(2024九上·嘉定月考)下列说法中,正确的是( )
A.如果和是相反向量,那么
B.如果和是平行向量,那么
C.如果,那么
D.如果,那么
5.(2021九上·松江期末)已知=2,那么下列判断错误的是( )
A.﹣2=0 B.
C.||=2|| D.
6.(2024九上·浦东期中)下列关于空间向量的命题中,正确命题的个数是( )
①任一向量与它的相反向量都不相等;
②长度相等、方向相同的两个向量是相等向量;
③平行且模相等的两个向量是相等向量;
④若a≠b,则|a|≠|b|;
⑤两个向量相等,则它们的起点与终点相同.
A.0 B.1 C.2 D.3
7.(2019·顺义模拟)规定:在平面直角坐标系xOy中,如果点P的坐标为(m,n),向量 可以用点P的坐标表示为: =(m,n).已知 =(x1,y1), =(x2,y2),如果x1x2+y1y2=0,那么 与 互相垂直.下列四组向量中,互相垂直的是( )
A. , B. ,
C. , D. ,
8.(2017·普陀模拟)如图,在△ABC中,中线AD、CE交于点O,设 = , = ,那么向量 用向量 、 表示为( )
A.+ B.+
C.+ D.+
9.(2024九上·崇明期中)下列说法中,正确的是( )
A.
B.如果,那么
C.如果是单位向量,那么
D.如果是非零向量,且,那么
二、填空题
10.(2023九上·闵行期中)过的重心作,分别交于点,于点,如果,那么 .
11.(2024九上·上海市月考)已知与单位向量的方向相反,且长度为4,那么表示为
12.(2024九下·上海市模拟)如图,已知在中,点D是边的中点,设,,用向量、表示向量 ,
13.(2016九上·浦东期中)如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB, ,那么 = .
14.(2024九下·虹口模拟)如图,已知在平行四边形中,点E是边的中点,和交于点F,设.用向量表示向量,即= .
15.(2019·徐汇模拟)如图,在梯形ABCD中,AD∥BC,EF是梯形ABCD的中位线,AH∥CD分别交EF、BC于点G、H,若 = , = ,则用 、 表示 = .
三、计算题
16.计算:
17.(2024九上·上海市期中)如图,已知向量、,求作向量并求作向量在向量、向量方向上的分向量.
四、解答题
18.(2022九上·杨浦模拟)如图,在梯形中,,,对角线、相交于点,设,.试用、的式子表示向量.
19.(2023九上·浦东期中)如图,点E是平行四边形ABCD边BC上一点,且BE:EC=2:1,点F是边CD的中点,AE与BF交于点O.
(1)设=,=,试用、表示;
(2)求BO:OF的值.
答案解析部分
1.【答案】D
【知识点】平面向量及其表示
2.【答案】D
【知识点】平行向量定理
3.【答案】C
【知识点】向量的加法法则
4.【答案】D
【知识点】平面向量及其表示
5.【答案】A
【知识点】实数与向量相乘运算法则;平行向量定理
6.【答案】B
【知识点】实数与向量相乘运算法则
7.【答案】B
【知识点】平面向量及其表示;向量的线性运算
8.【答案】B
【知识点】实数与向量相乘运算法则
9.【答案】D
【知识点】平面向量及其表示
10.【答案】
【知识点】向量的线性运算
11.【答案】
【知识点】向量的线性运算
12.【答案】
【知识点】向量的线性运算
13.【答案】2 ﹣
【知识点】向量的加法运算律
14.【答案】
【知识点】向量的线性运算
15.【答案】 .
【知识点】向量的线性运算
16.【答案】原式=
【知识点】向量的加法法则;实数与向量相乘的运算律
17.【答案】解:
,
如图,向量即为所作:
向量即为在向量方向上的分向量,
向量即为在向量方向上的分向量.
【知识点】实数与向量相乘运算法则;向量的线性运算
18.【答案】
【知识点】实数与向量相乘运算法则
19.【答案】(1)解:∵BE:EC=2:1,,
∴,
∴;
(2)解:
过点E作EM∥CD,
则,,
∵点F是CD中点,
∴,
设OM=a,则BO=3a,MF=2a,
故可得.
【知识点】平行向量定理;向量的线性运算
21世纪教育网(www.21cnjy.com)
7 / 7
同课章节目录
