【模型攻关】2025年中考复习培优专项训练:正方形中的十字架模型 (含答案)
文档属性
| 名称 | 【模型攻关】2025年中考复习培优专项训练:正方形中的十字架模型 (含答案) | 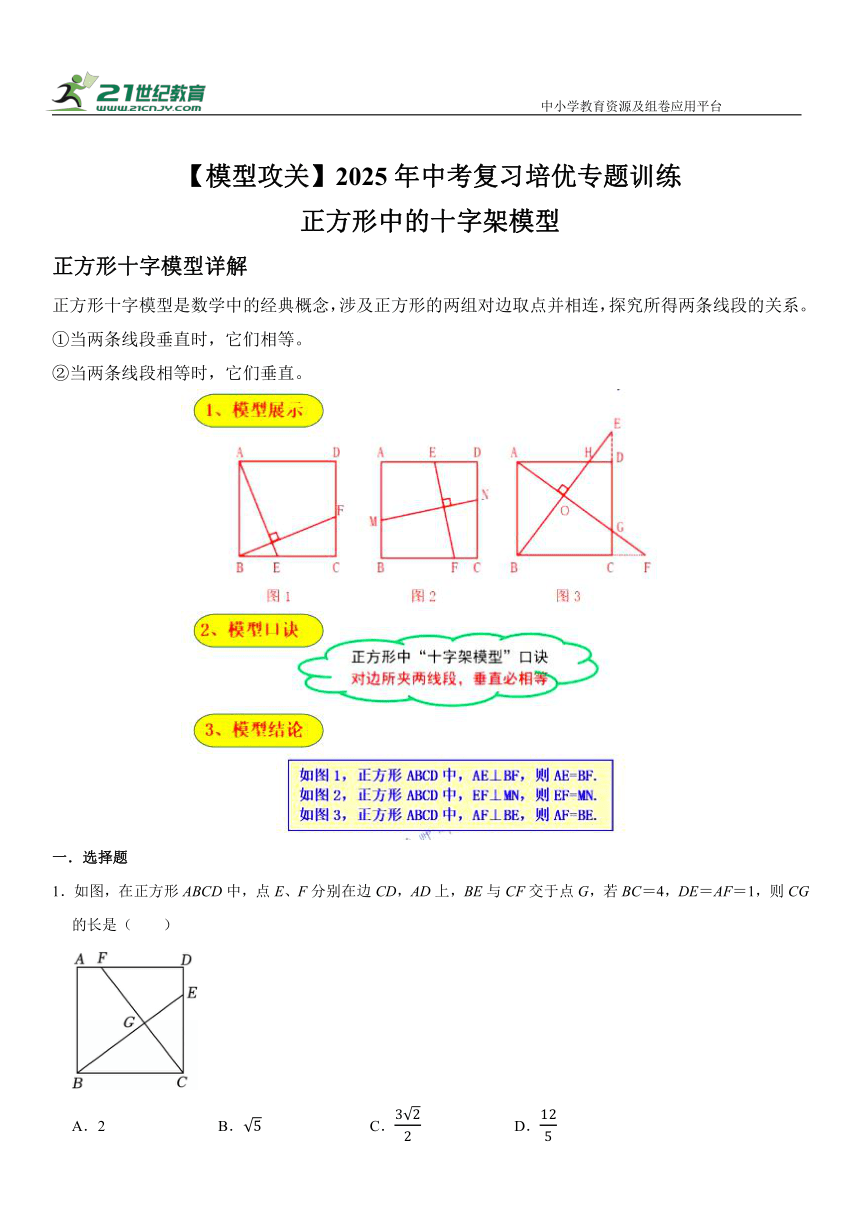 | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 15:48:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【模型攻关】2025年中考复习培优专题训练
正方形中的十字架模型
正方形十字模型详解
正方形十字模型是数学中的经典概念,涉及正方形的两组对边取点并相连,探究所得两条线段的关系。
①当两条线段垂直时,它们相等。
②当两条线段相等时,它们垂直。
一.选择题
1.如图,在正方形ABCD中,点E、F分别在边CD,AD上,BE与CF交于点G,若BC=4,DE=AF=1,则CG的长是( )
A.2 B. C. D.
2.如图,点E、F、G分别是正方形ABCD的边AD、BC、AB上的点,连接DG,EF,GF.且EF=DG,DE=2AG,∠ADG的度数为α,则∠EFG的度数为( )
A.α B.2α C.45°﹣α D.45°+α
3.如图,正方形ABCD中,AE=DF,AF与BE相交于点H,点O为BD中点,连结OH,若DG=OG,则的值为( )
A. B. C. D.
4.如图,在正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接AF与BE相交于点G.若AG+BG=6,空白部分面积为10.5,则AB的长为( )
A.3 B. C.2 D.
5.如图所示,E、F、G、H分别为正方形ABCD的边AB,BC,CD,DA上的点,且AE=BF=CG=DHAB,则图中阴影部分的面积与正方形ABCD的面积之比为( )
A. B. C. D.
6.如图,在正方形ABCD中,E为BC的中点,F为CD的中点,AE和BF相交于点G,延长CG交AB于点H,下列结论:
①AE=BF;
②∠CBF=∠DGF;
③;
④.
其中结论正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二.填空题
7.如图,在正方形ABCD中,点E,F分别是BC,CD上的点,AE与BF相交于点G,连接AC交BF于点H.若CE=DF,BG=GH,AB=2,则△CFH的面积为 .
8.如图,在正方形ABCD中,点E,F分别在BC,AB上,且DE=DF,AC分别交DE,DF于点M,N.设△DMN和△AFN的面积分别为S1和S2,若S2=2S1,则tan∠ADF的值为 .
9.如图,E,F分别是正方形ABCD的边CB,AD上的点,且CE=DF,AE与BF相交于O.下列结论:①AE=BF且AE⊥BF;②S△AOB=S四边形DEOF;③AD=OE;④连接OC,当E为边DC的中点时,tan∠EOC值为,其中正确的结论有 .
10.如图,现有边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A点D重合),将正方形纸片沿EF折叠,使点B落在P处,点C落在G处,PG交DC于H,连结BP、BH,下列结论:
①BP=EF;
②当P为AD中点时,△PAE三边之比为3:4:5;
③∠APB=∠BPH;
④△PDH周长等于8.
其中正确的是 (写出所有正确结论的序号)
三.解答题
11.如图,A,B,C,D四家工厂分别坐落在正方形城镇的四个角上,仓库P和Q分别位于AD和DC上,且PD=QC.问题:此时BP与AQ有怎样的关系?请说明理由.
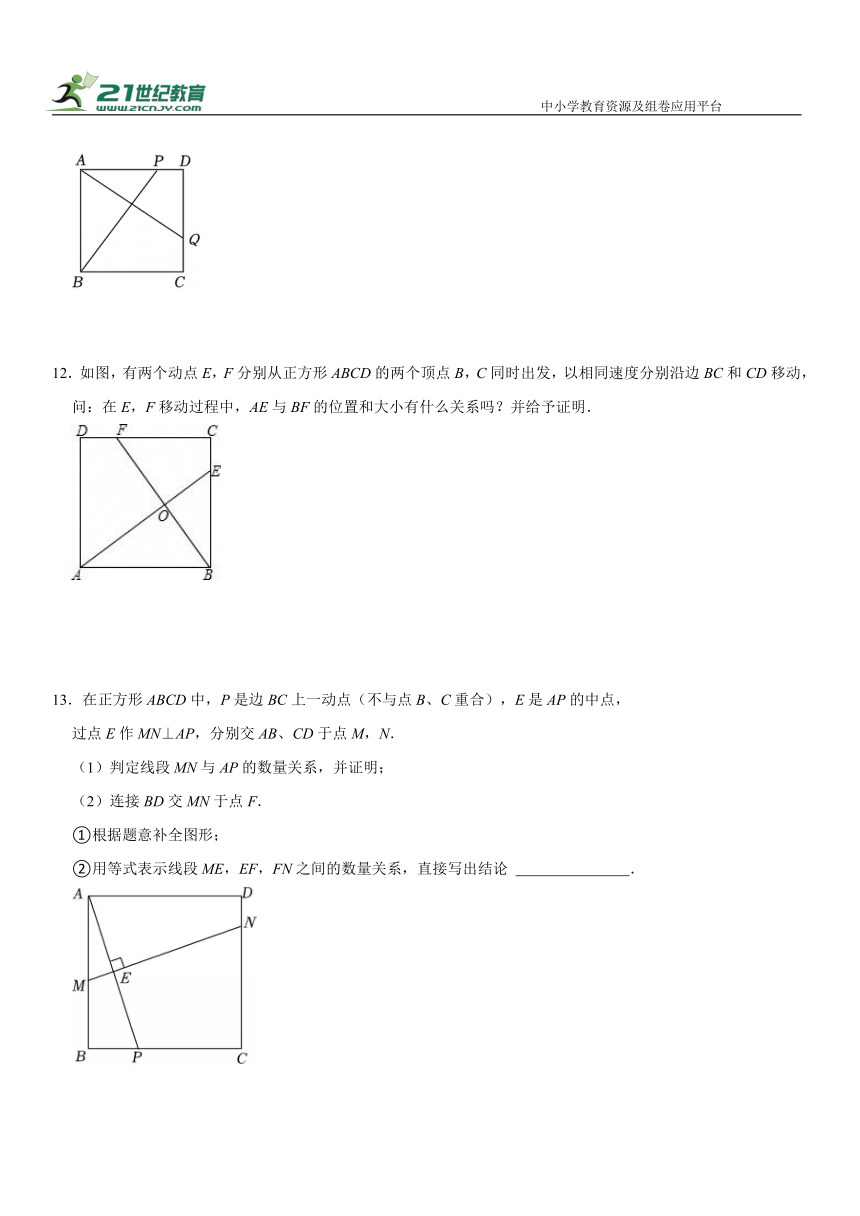
12.如图,有两个动点E,F分别从正方形ABCD的两个顶点B,C同时出发,以相同速度分别沿边BC和CD移动,问:在E,F移动过程中,AE与BF的位置和大小有什么关系吗?并给予证明.
13.在正方形ABCD中,P是边BC上一动点(不与点B、C重合),E是AP的中点,
过点E作MN⊥AP,分别交AB、CD于点M,N.
(1)判定线段MN与AP的数量关系,并证明;
(2)连接BD交MN于点F.
①根据题意补全图形;
②用等式表示线段ME,EF,FN之间的数量关系,直接写出结论 .
14.如图1,在正方形ABCD中,,点E在边BC上,连接AE,且∠BAE=30°,点F是AE的中点.
(1)求AE的长;
(2)过点F作直线GH,分别交AB,CD于点G,H,且GH=AE,求AG的长;
(3)如图2,过点F作AE的垂线,分别交AB,BD,CD于点M,O,N,连接OE,求∠AEO的度数.
15.问题情境:苏科版八年级下册数学教材第94页第19题第(1)题是这样一个问题:
如图1,在正方形ABCD中,点E、F分别在边BC、CD上,且AE⊥BF,垂足为M.那么AE与BF相等吗?
(1)直接判断:AE BF(填“=”或“≠”);
在“问题情境”的基础上,继续探索:
问题探究:
(2)如图2,在正方形ABCD中,点E、F、G分别在边BC、CD和DA上,且GE⊥BF,垂足为M.那么GE与BF相等吗?证明你的结论;
问题拓展:
(3)如图3,点E在边CD上,且MN⊥AE,垂足为H,当H在正方形ABCD的对角线BD上时,连接AN,将△AHN沿着AN翻折,点H落在点H′处.
①四边形AHNH′是正方形吗?请说明理由;
②若AB=6,点P在BD上,BD=3BP,直接写出PH′AN的最小值为 .
16.问题背景:某课外学习小组在一次学习研讨中,得到了如下两个命题:
①如图1,在正三角形ABC中,M,N分别是AC,AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;
②如图2,在正方形ABCD中,M,N分别是CD,AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类比的思想提出了如下命题;
③如图3,在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:
(1)请你从①,②,③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索:
①如图4,在正n(n≥3)边形ABCDEF…中,M,N分别是CD,DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立;(不要求证明)
②如图5,在正五边形ABCDE中,M,N分别是DE,AE上的点,BM与CN相交于点O,若∠BON=108°时,试问结论BM=CN是否还成立.若成立,请给予证明;若不成立,请说明理由.
参考答案
一.选择题
1.解:∵四边形ABCD为正方形,BC=4,
∴∠CDF=∠BCE=90°,AD=DC=BC=4,
又∵DE=AF=1,
∴CE=DF=3,
在△CDF和△BCE中,
,
∴△CDF≌△BCE (SAS),
∴∠DCF=∠CBE,
∵∠DCF+∠BCF=90°,
∴∠CBE+∠BCF=90°,
∴∠BGC=90°,
在Rt△BCE中,BC=4,CE=3,
∴BE5,
∴BE CG=BC CE,
∴CG.
故选:D.
2.解:∵四边形ABCD为正方形,
∴AB=BC=CD=AD,∠A=∠B=∠C=∠ADC=90°,
如图,过点F作FH⊥AD于点H,
则四边形CDHF为矩形,
∴FH=CD,DH=CF,∠FHE=90°,
∴FH=AD,
在Rt△FHE和Rt△DAG中,
,
∴Rt△FHE≌Rt△DAG(HL),
∴EH=AG,∠HFE=∠ADG=α,
∵DE=AG,
∴DE=2EH,即点D为DE中点,
∴EH=DH=AG=CF,
∴AB﹣AG=BC﹣CF,即BG=BF,
∴△BFG为等腰直角三角形,∠BFG=45°,
∴∠EFG=90°﹣∠BFG﹣∠HFE=90°﹣45°﹣α=45°﹣α.
故选:C.
3.解:∵四边形ABCD是正方形,
∴AD=AB,∠ADC=∠DAB=90°,
又∵DF=AE,
∴△DAF≌△ABE(SAS),
∴BE=AF,∠EBA=∠EAH,
∵∠EAH+∠HAB=90°,
∴∠EBA+∠HAB=90°,
∴∠AHB=90°,
∵点O为BD中点,DG=OG,
∴,
∵AB∥CD,
∴△DFG∽△BAG,
∴,
设DF=k,则AB=3k,
∴AE=k,
在Rt△AEB中,EB,
∴,解得AH,
在Rt△AHB中,根据勾股定理BH,
过点O作OP⊥AB于点P,过H作HN⊥AB于点N,过O作OM⊥NH交NH的延长线于点M,如图:
则四边形OMNP为矩形,
∴OM=NP,OP=MN,
在Rt△AHB中,3k HN=AH BH,
∴HN,
∴MH,
又∵∠EBA=∠AHN,∠HNA=∠EAB,
∴△HNA∽△BAE,
∴,
∴AN,
∴NP=OM,
根据勾股定理可得OH,
∴,
故选:A.
4.解:∵四边形ABCD为正方形,
∴∠D=∠BAD=90°,AD=AB,
在△ADF和△BAE中,
,
∴△ADF≌△BAE(SAS),
∴S△ADF=S△BAE,∠DAF=∠ABE,
∵∠BAG+∠DAF=90°,
∴∠BAG+∠ABE=90°,
∴∠AGB=90°,即BG⊥AG,
∵S△ADF=S△BAE,
∴S△ADF﹣S△AEG=S△BAE﹣S△AEG,即S四边形DEGF=S△ABG,
∵AG+BG=6,
∴(AG+BG)2=AG2+BG2+2AG BG=36,
∵S△ABG,AB2=AG2+BG2,
∴AB2+4S△ABG=36,即,
∵S空白=S正方形ABCD﹣S四边形DEGF﹣S△ABG=S正方形ABCD﹣2S△ABG10.5,
解得:AB(负值已舍去).
故选:B.
5.解:
∵四边形ABCD是正方形,
∴BC=AB=AD,∠DAB=∠ABF=90°,
∵AEAB,BFBC,
∴△DAE≌△ABF(SAS),
∴∠ADM=∠BAN,
∵∠BAN+∠DAM=90°,
∴∠ADM+DAM=90°,
∴∠AMD=90°,
同理:∠ANB=90°,
∴∠AMD=∠ANB,
∴△DAM≌△ABN(AAS),
∴AM=BN,
同理可以证明△BCP,△CDQ,△DAM,△ABN是全等的直角三角形,它们的面积相等,
∵BEAB,DGDC,AB∥DC,
∴四边形EBGD是平行四边形,
∴ED∥BG,
∴AM:AN=AE:AB=1:4,
令正方形ABCD的边长是a,AM=b,则BN=b,AN=4b,
∴正方形ABCD的面积是a2,△ABN的面积是b 4b=2b2,
∵AB2=BN2+AN2,
∴a2=b2+16b2=17b2,
∵阴影的面积=a2﹣4×2b2=17b2﹣8b2=9b2,
∴阴影部分的面积与正方形ABCD的面积的比是.
故选:A.
6.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠ADC=90°,AB∥CD,
∵E为BC的中点,F为CD的中点,
∴BEBC,CFCD,
∴BE=CF,
∴△ABE≌△BCF(SAS),
∴BF=AE,∠BAE=∠CBF,
故①正确,
∵∠CBF+∠ABF=90°,
∴∠ABF+∠BAE=90°,
∴∠AGB=180°﹣(∠BAE+∠ABF)=90°,
∴AE⊥BF,
∴∠AGF=90°,
延长BF交AD的延长线于点M,
∵∠MDF=∠BCF=90°,DF=CF,∠DFM=∠BFC,
∴△BFC≌△MFD(ASA),
∴DM=BC,∠M=∠MBC,
∴AD=DM,
∴DG=DMAM,
∴∠DGM=∠M,
∴∠CBF=∠DGF,
故②正确;
设BE=CF=a,则AB=BC=2a,
∴AEa,
∴BF=AEa,
∵△ABE的面积AB BEAE BG,
∴BGa,
∴FG=BF﹣BGa,
∵AB∥CD,
∴∠ABG=∠BFC,∠BHG=∠HCF,
∴△BHG∽△FCG,
∴,
∴,
故③正确;
∵,CF=3a,
∴BH=2a,
∴AH=AB﹣BH=4a,
∴,
∵△AHG中AH边上的高与△GCF中CF边上的高不相等,
∴,
故④不正确;
综上所述:正确的结论是:①②③,
故选:A.
二.填空题
7.解:如图:过点H作HM⊥CD,垂足为M,
∵四边形ABCD是正方形,
∴AB=BC=CD=2,AB∥CD,∠ABC=∠BCD=90°,∠ACD=45°,
∴ACAB=2,
∵CE=DF,
∴BC﹣CE=CD﹣DF,
∴BE=CF,
∴△ABE≌△BCF(SAS),
∴∠1=∠2,
∵∠ABC=∠2+∠3=90°,
∴∠1+∠3=90°,
∴∠AGB=180°﹣(∠1+∠3)=90°,
∵BG=GH,
∴AG是BH的垂直平分线,
∴AB=AH=2,
∴∠3=∠AHB,CH=AC﹣AH=22,
∵AB∥CD,
∴∠3=∠CFH,
∵∠AHB=∠CHF,
∴∠CFH=∠CHF,
∴CH=CF=22,
在Rt△HMC中,HM2,
∴△CFH的面积CF HM(22)×(2)=34,
故答案为:34.
8.解:过N作NH⊥AB于H,如图:
∵∠FHN=∠FAD=90°,
∴HN∥AD,
∴∠ADF=∠HNF,
设tan∠ADF=tan∠FNH=k,设NH=AH=b,则FH=kb,
∴AF=b+kb,
∵tan∠ADF,
∴ADb,
∴S2AF HNb2(1+k),S1=S△ADC﹣2S△ADN(b)2﹣2 b b,
∵S2=2S1,
∴b2(1+k)=2 [(b)2﹣2 b b],
整理得:k2+2k﹣2=0,
解得:k1或1(舍弃),
∴tan∠ADF=k1,
故答案为:1.
9.解:∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠ADE=90°.
∵CE=DF,
∴AF=DE.
在△ABF和△DAE中,
,
∴△ABF≌△DAE(SAS).
∴AE=BF,故①正确.
∵△ABF≌△DAE,
∴∠AFB=∠AED.
∵∠AED+∠DAE=90°,
∴∠AFB+∠DAE=90°,
∴∠AOF=90°,即AE⊥BF,故①正确.
∵△ABF≌△DAE,
∴S△ABF=S△ADE.
∴S△AOB=S△ABF﹣S△AOF,S四边形DEOF=S△ADE﹣S△AOF,即S△AOB=S四边形DEOF,故②正确.
如图过点E作EM⊥AB,交于点M,连接OM,
在正方形ABCD中,
∠BAD=∠ADE=∠AME=90°,
∴四边形ADEM为矩形,
AD=EM,
在△OME中,
∵∠EOM为钝角,
∴△EOM不是以点E为顶点的等腰△,
∴OE≠EM,
即AD≠OE,
故③错误.
如图,连接OC,延长AE使AE=EG,交BC延长线于点G,过点C作CH⊥AG交于点H,
∵E是边DC的中点,
∴ED=EC,
在△ADE和△GCE中,
,
∴△ADE≌△GCE(SAS),
所以∠ECG=∠EDA=90°=∠BCE,
∴点B、C、G共线,
∴∠G=∠GAD
设边AD=DC=2a,
∴AF=DE=a,
tan∠GAD,
∴tan∠CGA,
AEa,
∴AG=2AE=2a,
∵CG=AD,
∴CG=2a,
在△CEG中,CHa,HGa,
在△AOF中,AOa,
∴OH=AG﹣HG﹣AOa,
在Rt△CHO中,tan∠EOC,
故④正确.
故答案为:①②④.
10.解:如图,过点F作FM⊥AB于点M,
∵四边形ABCD为正方形,
∴∠A=∠ABC=90°,AB=BC,
∵FM⊥AB,
∴四边形MBCF为矩形,
∴MF=BC=AB,∠FME=90°,
由折叠可知,EF⊥BP,
∴∠PBE+∠BEF=90°,
∵∠PBE+∠APB=90°,
∴∠BEF=∠APB,即∠MEF=∠APB,
在△ABP和△MFE中,
,
∴△ABP≌△MFE(AAS),
∴BP=EF,故①正确;
由折叠可知,BE=PE,
设BE=PE=x,则AE=4﹣x,
∵P为AD中点,
∴AP=2,
在Rt△PAE中,AP2+AE2=PE2,
∴22+(4﹣x)2=x2,
解得:x,
∴AE=4﹣x,PE,
∴AE:AP:PE:2:3:4:5,
即△PAE三边之比为3:4:5,故②正确;
由折叠可知,BE=PE,∠EBC=∠EPG=90°,
∴∠PBE=∠BPE,∠BPE+∠BPH=90°,
∵∠PBE+∠APB=90°,
∴∠APB=∠BPH,故③正确;
如图,过点B作BN⊥PH于点N,
∴∠BAP=∠BNP=90°,
在△ABP和△NBP中,
,
∴△ABP≌△NBP(AAS),
∴AB=BN,AP=PN,
∴BC=BN,
在Rt△BNH和Rt△BCH中,
,
∴Rt△BNH≌Rt△BCH(HL),
∴NH=CH,
∴C△PDH=PD+PN+NH+DH=PD+AP+CH+DH=2AD=8,故④正确.
综上,正确的结论有①②③④.
故答案为:①②③④.
三.解答题
11.解:如图所示:
BP与AQ互相垂直且相等,理由如下:
∵四边形ABCD是正方形,
∴AB=AD=CD,∠BAP=∠ADQ=90°,
∵PD=QC,
∴AD﹣PD=CD﹣QC,即AP=DQ,
在△ABP和△DAQ中,
,
∴△ABP≌△DAQ(SAS),
∴BP=AQ,∠ABP=∠DAQ,
∵四边形ABCD是正方形,
∴AD∥BC,∠ABC=90°,
∴∠APB=∠PBC,
∵∠ABP+∠PBC=∠ABC=90°,
∴∠DAQ+∠APB=90°,
∵∴∠DAQ+∠APB+∠AOP=180°,
∴∠AOP=180°﹣(∠DAQ+∠APB)=90°,
∴BP⊥AQ,
∴BP与AQ互相垂直且相等.
12.解:AE与BF的位置关系是:垂直;大小关系是:相等.
证明:∵四边形ABCD为正方形,
∴AB=BC,∠ABC=∠BCD=90°,
又动点E,F分别从正方形ABCD的两个顶点B,C同时出发,以相同速度分别沿边BC和CD移动,
∴BE=CF,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(SAS),
∴∠EAB=∠FBC,AE=BF,
∵∠CBF+∠ABO=90°,
∴∠EAB+∠ABO=90°,
在△ABO中,∠AOB=180°﹣(∠EAB+∠ABO)=90°,
∴AE⊥BF.
13.解:(1)MN=AP.
证明:过点M作MG⊥CD于点G,则四边形AMGD是矩形,
∴MG=AD,∠MGN=90°,
∵四边形ABCD是正方形,
∴∠ABP=90°,AB=BC=AD,
∴MG=AB,∠ABP=∠MGN,
又∵MN⊥AP,
∴∠AEM=90°,
∴∠AME+∠BAP=90°,
又∵∠NMG+∠AME=90°,
∴∠NMG=∠BAP,
∴△ABP≌△MGN(ASA),
∴AP=MN;
(2)①补全图形如图2,
②如图3,过点P作PH∥AB交MN于点H,交BD于点K,过点M作MG⊥CD于点G,
∵AM∥PH,
∴∠MAE=∠EPH,
∵E为AP的中点,
∴AE=EP,
又∵∠AEM=∠PEH,
∴△AME≌△PHE(ASA),
∴ME=EH,AM=PH,
∵四边形AMGD是矩形,
∴AM=DG,
∴DG=PH,
∵∠CBD=45°,∠BPK=90°,
∴∠PBK=∠BKP=45°,
∴BP=PK,
由(1)知△ABP≌△MGN,
∴BP=NG,
∴PK=NG,
∴HK=DN,
又∵NK∥DN,
∴∠HKF=∠NDF,
∴△HKF≌△NDF(AAS),
∴HF=NF,
∴EF=EH+HF=EM+FN.
故答案为:EF=EM+FN.
14.解:(1)∵∠BAE=30°,
∴AE=2BE,
设BE=x,则AE=2x,
在Rt△ABE中,x2(2x)2,
解得x=2或﹣2(舍去),
∴AE=4;
(2)如图,过点B作BR∥GH,交CD于R,
∵GH∥BR,AB∥CD,
∴四边形BRHG是平行四边形,
∴GH=BR,∠BGH=∠BRH,
∵GH=AE,
∴BR=GH=AE.
又∵AB=BC,
∴Rt△ABE≌Rt△BCR(HL),
∴∠BAE=∠CBR=30°,
∴∠BRC=60°=∠AEB,
∴∠BRH=120°=∠BGH,
∴∠AGH=60°,
∴∠AFG=180°﹣60°﹣30°=90°,
∵∠BAE=30°,
∴AG=2GF,
∴AG2=GF2﹣AF2,
∴3GF2=4.
∴GF,
∴AG;
如图,过点A作AR∥GH,交CD于R,过点G作GO⊥AE于点O,
同理可证:△ABE≌△ADR,
∴∠DAR=∠BAE=30°,
∴∠EAR=30°,
∵AR∥GH,
∴∠RAF=∠AFG=30°,
∴∠BAE=∠AFG,
∴AG=GF,
∵GO⊥AF,
∴AO=FO=1,
∵∠BAE=30°,
∴AG=2GO,
∴AG2﹣GO2=AO2,
∴3GO2=1,
∴GO,
∴AG,
∴AG的长为或;
(3)如图,连接AO,过点O作OQ⊥AB于点Q,OP⊥BC于点P,
∵四边形ABCD是正方形,
∴∠ABD=∠CBD=45°,
∵OQ⊥AB,OP⊥BC,
∴OQ=OP,
∵MN⊥AE,AE=EF,
∴AO=OE,
∴∠OAE=∠OEA,
∵OA=OE,OQ=OP,
∴Rt△AOQ≌Rt△EOP(HL),
∴∠OAQ=∠OEP,
∵∠BEA+∠AEO+∠OEP=180°,
∴60°+∠AEO+∠OAE+30°=180°,
∴∠AEO=45°.
15.解:(1)∵AE⊥BF,
∴∠EMB=90°,
∴∠FBC+∠BEM=90°,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∴∠FBC+∠BFC=90°,
∴∠BEM=∠BFC,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(AAS),
∴AE=BF.
故答案为:=;
(2)GE=BF,理由如下:
如图2,过点A作AN∥GE,交BF于点H,交BC于点N,
∴∠EMB=∠NHB=90°,
∴∠FBC+∠BNH=90°,
∵四边形ABCD是正方形,
∴AD∥BC,AB=BC,∠BAD=∠ABC=∠C=90°,
∵AD∥BC,AN∥GE,
∴四边形ANEG是平行四边形,
∴AN=EG,
∵∠C=90°,
∴∠FBC+∠BFC=90°,
∴∠BNH=∠BFC,
∴△ABN≌△BCF(AAS),
∴AN=BF,
∵AN=EG,
∴GE=BF.
(3)①如图3,连接CH,
由(2)的结论可知,AE=MN,
∵四边形ABCD是正方形,BD是正方形的对角线,
∴∠ABD=∠CBD=45°,AB=BC,
∵BH=BH,
∴△ABH≌△CBH(SAS),
∴∠BAH=∠BCH,AH=CH,
由折叠可知,AH=AH′,NH=NH′,
∵∠ABN+∠AHN=180°,
∴∠BAH+∠BNH=180°,
∵∠BNH+∠HNC=180°,
∴∠BAH=∠HNC,
∴∠HNC=∠NCH,
∴NH=CH,
∴NH=CH=AH=AH′=NH′,
∴四边形AHNH′是菱形,
∵∠AHN=90°,
∴菱形AHNH′是正方形;
②如图4,作H′Q⊥BC交CB的延长线于点Q,作HF⊥BC于点M,
∴∠H′QN=∠HFB=90°,
由上知四边形AHNH′是正方形,
∴H′N=HN,∠H′NH=90°,AH′AN,
∴∠H′NQ+∠HNF=∠HNF+∠NHF=90°,
∴∠H′NQ=∠NHF,
∴△H′QN≌△NFH′(AAS),
∴H′Q=NF,QN=HF;
∵∠HBF=45°,∠HFB=90°,
∴△BHF是等腰直角三角形,
∴HF=BF=NF+BN,
∵QN=QB+BN,
∴NF=QB=QH′,
∴∠H′BQ=∠ABH′=45°,
∴∠H′BD=90°;
如图4,作P关于BH′的对称点P′,则PH′=P′H′,过点P′作PK⊥AB交AB延长线于点K,
则△PBK是等腰直角三角形,
∴PH′AN=PH′+AH′=P′H′+AH′≥AP′,即当A,H′,P′三点共线时,PH′AN最小,最小值为AP′的长.
∵AB=6,
∴BD=6,
∵BD=3BP,
∴BP=BP′=2,
∴PK=BK=2,
∴AK=8,
∴AP′2,即PH′AN的最小值为2.
故答案为:2.
16.
解:(1)选命题①
在图1中,∵△ABC是正三角形,
∴BC=CA,∠BCM=∠CAN=60°.
∵∠BON=60°,
∴∠CBM+∠BCN=60°.
∵∠BCN+∠ACN=60°,
∴∠CBM=∠ACN.
∴△BCM≌△CAN(ASA).
∴BM=CN.
选命题②
在图2中∵四边形ABCD是正方形,
∴BC=CD,∠BCM=∠CDN=90°.
∵∠BON=90°,
∴∠CBM+∠BCN=90°.
∵∠BCN+∠DCN=90°,
∴∠CBM=∠DCN.
∴△BCM≌△CDN(ASA).
∴BM=CN.
选命题③
在图3中,∵五边形ABCDE是正五边形,
∴BC=CD,∠BCM=∠CDN=108°.
∵∠BON=108°,
∴∠CBM+∠BCN=108°.
∵∠BCN+∠DCN=108°,
∴∠CBM=∠DCN.
∴△BCM≌△CDN(ASA).
∴BM=CN.
(2)①当∠BON时,结论BM=CN成立.
②BM=CN成立.
在图5中,连接BD、CE,
∵五边形ABCDE是正五边形,
∴BC=CD,∠BCD=∠CDE=108°,CD=DE,∠CDE=∠DEA=108°.
∴∠BCD=∠DEA,
∴△BCD≌△CDE(SAS).
∴BD=CE,∠BDC=∠CED,∠DBC=∠ECD.
∵∠BON=108°,
∴∠OBC+∠OCB=108°.
∵∠OCB+∠OCD=108°,
∴∠OBC=∠OCD(即∠MBC=∠NCD).
∴∠MBC﹣∠DBC=∠NCD﹣∠ECD,即∠DBM=∠ECN.
∴∠CDE﹣∠BDC=∠DEA﹣∠CED,即∠BDM=∠CEN.
∴△BDM≌△CEN(ASA).
∴BM=CN.
【模型攻关】2025年中考复习培优专题训练
正方形中的十字架模型
正方形十字模型详解
正方形十字模型是数学中的经典概念,涉及正方形的两组对边取点并相连,探究所得两条线段的关系。
①当两条线段垂直时,它们相等。
②当两条线段相等时,它们垂直。
一.选择题
1.如图,在正方形ABCD中,点E、F分别在边CD,AD上,BE与CF交于点G,若BC=4,DE=AF=1,则CG的长是( )
A.2 B. C. D.
2.如图,点E、F、G分别是正方形ABCD的边AD、BC、AB上的点,连接DG,EF,GF.且EF=DG,DE=2AG,∠ADG的度数为α,则∠EFG的度数为( )
A.α B.2α C.45°﹣α D.45°+α
3.如图,正方形ABCD中,AE=DF,AF与BE相交于点H,点O为BD中点,连结OH,若DG=OG,则的值为( )
A. B. C. D.
4.如图,在正方形ABCD中,点E、F分别在AD、CD上,且AE=DF,连接AF与BE相交于点G.若AG+BG=6,空白部分面积为10.5,则AB的长为( )
A.3 B. C.2 D.
5.如图所示,E、F、G、H分别为正方形ABCD的边AB,BC,CD,DA上的点,且AE=BF=CG=DHAB,则图中阴影部分的面积与正方形ABCD的面积之比为( )
A. B. C. D.
6.如图,在正方形ABCD中,E为BC的中点,F为CD的中点,AE和BF相交于点G,延长CG交AB于点H,下列结论:
①AE=BF;
②∠CBF=∠DGF;
③;
④.
其中结论正确的是( )
A.①②③ B.①②④ C.①③④ D.②③④
二.填空题
7.如图,在正方形ABCD中,点E,F分别是BC,CD上的点,AE与BF相交于点G,连接AC交BF于点H.若CE=DF,BG=GH,AB=2,则△CFH的面积为 .
8.如图,在正方形ABCD中,点E,F分别在BC,AB上,且DE=DF,AC分别交DE,DF于点M,N.设△DMN和△AFN的面积分别为S1和S2,若S2=2S1,则tan∠ADF的值为 .
9.如图,E,F分别是正方形ABCD的边CB,AD上的点,且CE=DF,AE与BF相交于O.下列结论:①AE=BF且AE⊥BF;②S△AOB=S四边形DEOF;③AD=OE;④连接OC,当E为边DC的中点时,tan∠EOC值为,其中正确的结论有 .
10.如图,现有边长为4的正方形纸片ABCD,点P为AD边上的一点(不与点A点D重合),将正方形纸片沿EF折叠,使点B落在P处,点C落在G处,PG交DC于H,连结BP、BH,下列结论:
①BP=EF;
②当P为AD中点时,△PAE三边之比为3:4:5;
③∠APB=∠BPH;
④△PDH周长等于8.
其中正确的是 (写出所有正确结论的序号)
三.解答题
11.如图,A,B,C,D四家工厂分别坐落在正方形城镇的四个角上,仓库P和Q分别位于AD和DC上,且PD=QC.问题:此时BP与AQ有怎样的关系?请说明理由.
12.如图,有两个动点E,F分别从正方形ABCD的两个顶点B,C同时出发,以相同速度分别沿边BC和CD移动,问:在E,F移动过程中,AE与BF的位置和大小有什么关系吗?并给予证明.
13.在正方形ABCD中,P是边BC上一动点(不与点B、C重合),E是AP的中点,
过点E作MN⊥AP,分别交AB、CD于点M,N.
(1)判定线段MN与AP的数量关系,并证明;
(2)连接BD交MN于点F.
①根据题意补全图形;
②用等式表示线段ME,EF,FN之间的数量关系,直接写出结论 .
14.如图1,在正方形ABCD中,,点E在边BC上,连接AE,且∠BAE=30°,点F是AE的中点.
(1)求AE的长;
(2)过点F作直线GH,分别交AB,CD于点G,H,且GH=AE,求AG的长;
(3)如图2,过点F作AE的垂线,分别交AB,BD,CD于点M,O,N,连接OE,求∠AEO的度数.
15.问题情境:苏科版八年级下册数学教材第94页第19题第(1)题是这样一个问题:
如图1,在正方形ABCD中,点E、F分别在边BC、CD上,且AE⊥BF,垂足为M.那么AE与BF相等吗?
(1)直接判断:AE BF(填“=”或“≠”);
在“问题情境”的基础上,继续探索:
问题探究:
(2)如图2,在正方形ABCD中,点E、F、G分别在边BC、CD和DA上,且GE⊥BF,垂足为M.那么GE与BF相等吗?证明你的结论;
问题拓展:
(3)如图3,点E在边CD上,且MN⊥AE,垂足为H,当H在正方形ABCD的对角线BD上时,连接AN,将△AHN沿着AN翻折,点H落在点H′处.
①四边形AHNH′是正方形吗?请说明理由;
②若AB=6,点P在BD上,BD=3BP,直接写出PH′AN的最小值为 .
16.问题背景:某课外学习小组在一次学习研讨中,得到了如下两个命题:
①如图1,在正三角形ABC中,M,N分别是AC,AB上的点,BM与CN相交于点O,若∠BON=60°,则BM=CN;
②如图2,在正方形ABCD中,M,N分别是CD,AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类比的思想提出了如下命题;
③如图3,在正五边形ABCDE中,M,N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求:
(1)请你从①,②,③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索:
①如图4,在正n(n≥3)边形ABCDEF…中,M,N分别是CD,DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立;(不要求证明)
②如图5,在正五边形ABCDE中,M,N分别是DE,AE上的点,BM与CN相交于点O,若∠BON=108°时,试问结论BM=CN是否还成立.若成立,请给予证明;若不成立,请说明理由.
参考答案
一.选择题
1.解:∵四边形ABCD为正方形,BC=4,
∴∠CDF=∠BCE=90°,AD=DC=BC=4,
又∵DE=AF=1,
∴CE=DF=3,
在△CDF和△BCE中,
,
∴△CDF≌△BCE (SAS),
∴∠DCF=∠CBE,
∵∠DCF+∠BCF=90°,
∴∠CBE+∠BCF=90°,
∴∠BGC=90°,
在Rt△BCE中,BC=4,CE=3,
∴BE5,
∴BE CG=BC CE,
∴CG.
故选:D.
2.解:∵四边形ABCD为正方形,
∴AB=BC=CD=AD,∠A=∠B=∠C=∠ADC=90°,
如图,过点F作FH⊥AD于点H,
则四边形CDHF为矩形,
∴FH=CD,DH=CF,∠FHE=90°,
∴FH=AD,
在Rt△FHE和Rt△DAG中,
,
∴Rt△FHE≌Rt△DAG(HL),
∴EH=AG,∠HFE=∠ADG=α,
∵DE=AG,
∴DE=2EH,即点D为DE中点,
∴EH=DH=AG=CF,
∴AB﹣AG=BC﹣CF,即BG=BF,
∴△BFG为等腰直角三角形,∠BFG=45°,
∴∠EFG=90°﹣∠BFG﹣∠HFE=90°﹣45°﹣α=45°﹣α.
故选:C.
3.解:∵四边形ABCD是正方形,
∴AD=AB,∠ADC=∠DAB=90°,
又∵DF=AE,
∴△DAF≌△ABE(SAS),
∴BE=AF,∠EBA=∠EAH,
∵∠EAH+∠HAB=90°,
∴∠EBA+∠HAB=90°,
∴∠AHB=90°,
∵点O为BD中点,DG=OG,
∴,
∵AB∥CD,
∴△DFG∽△BAG,
∴,
设DF=k,则AB=3k,
∴AE=k,
在Rt△AEB中,EB,
∴,解得AH,
在Rt△AHB中,根据勾股定理BH,
过点O作OP⊥AB于点P,过H作HN⊥AB于点N,过O作OM⊥NH交NH的延长线于点M,如图:
则四边形OMNP为矩形,
∴OM=NP,OP=MN,
在Rt△AHB中,3k HN=AH BH,
∴HN,
∴MH,
又∵∠EBA=∠AHN,∠HNA=∠EAB,
∴△HNA∽△BAE,
∴,
∴AN,
∴NP=OM,
根据勾股定理可得OH,
∴,
故选:A.
4.解:∵四边形ABCD为正方形,
∴∠D=∠BAD=90°,AD=AB,
在△ADF和△BAE中,
,
∴△ADF≌△BAE(SAS),
∴S△ADF=S△BAE,∠DAF=∠ABE,
∵∠BAG+∠DAF=90°,
∴∠BAG+∠ABE=90°,
∴∠AGB=90°,即BG⊥AG,
∵S△ADF=S△BAE,
∴S△ADF﹣S△AEG=S△BAE﹣S△AEG,即S四边形DEGF=S△ABG,
∵AG+BG=6,
∴(AG+BG)2=AG2+BG2+2AG BG=36,
∵S△ABG,AB2=AG2+BG2,
∴AB2+4S△ABG=36,即,
∵S空白=S正方形ABCD﹣S四边形DEGF﹣S△ABG=S正方形ABCD﹣2S△ABG10.5,
解得:AB(负值已舍去).
故选:B.
5.解:
∵四边形ABCD是正方形,
∴BC=AB=AD,∠DAB=∠ABF=90°,
∵AEAB,BFBC,
∴△DAE≌△ABF(SAS),
∴∠ADM=∠BAN,
∵∠BAN+∠DAM=90°,
∴∠ADM+DAM=90°,
∴∠AMD=90°,
同理:∠ANB=90°,
∴∠AMD=∠ANB,
∴△DAM≌△ABN(AAS),
∴AM=BN,
同理可以证明△BCP,△CDQ,△DAM,△ABN是全等的直角三角形,它们的面积相等,
∵BEAB,DGDC,AB∥DC,
∴四边形EBGD是平行四边形,
∴ED∥BG,
∴AM:AN=AE:AB=1:4,
令正方形ABCD的边长是a,AM=b,则BN=b,AN=4b,
∴正方形ABCD的面积是a2,△ABN的面积是b 4b=2b2,
∵AB2=BN2+AN2,
∴a2=b2+16b2=17b2,
∵阴影的面积=a2﹣4×2b2=17b2﹣8b2=9b2,
∴阴影部分的面积与正方形ABCD的面积的比是.
故选:A.
6.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠ADC=90°,AB∥CD,
∵E为BC的中点,F为CD的中点,
∴BEBC,CFCD,
∴BE=CF,
∴△ABE≌△BCF(SAS),
∴BF=AE,∠BAE=∠CBF,
故①正确,
∵∠CBF+∠ABF=90°,
∴∠ABF+∠BAE=90°,
∴∠AGB=180°﹣(∠BAE+∠ABF)=90°,
∴AE⊥BF,
∴∠AGF=90°,
延长BF交AD的延长线于点M,
∵∠MDF=∠BCF=90°,DF=CF,∠DFM=∠BFC,
∴△BFC≌△MFD(ASA),
∴DM=BC,∠M=∠MBC,
∴AD=DM,
∴DG=DMAM,
∴∠DGM=∠M,
∴∠CBF=∠DGF,
故②正确;
设BE=CF=a,则AB=BC=2a,
∴AEa,
∴BF=AEa,
∵△ABE的面积AB BEAE BG,
∴BGa,
∴FG=BF﹣BGa,
∵AB∥CD,
∴∠ABG=∠BFC,∠BHG=∠HCF,
∴△BHG∽△FCG,
∴,
∴,
故③正确;
∵,CF=3a,
∴BH=2a,
∴AH=AB﹣BH=4a,
∴,
∵△AHG中AH边上的高与△GCF中CF边上的高不相等,
∴,
故④不正确;
综上所述:正确的结论是:①②③,
故选:A.
二.填空题
7.解:如图:过点H作HM⊥CD,垂足为M,
∵四边形ABCD是正方形,
∴AB=BC=CD=2,AB∥CD,∠ABC=∠BCD=90°,∠ACD=45°,
∴ACAB=2,
∵CE=DF,
∴BC﹣CE=CD﹣DF,
∴BE=CF,
∴△ABE≌△BCF(SAS),
∴∠1=∠2,
∵∠ABC=∠2+∠3=90°,
∴∠1+∠3=90°,
∴∠AGB=180°﹣(∠1+∠3)=90°,
∵BG=GH,
∴AG是BH的垂直平分线,
∴AB=AH=2,
∴∠3=∠AHB,CH=AC﹣AH=22,
∵AB∥CD,
∴∠3=∠CFH,
∵∠AHB=∠CHF,
∴∠CFH=∠CHF,
∴CH=CF=22,
在Rt△HMC中,HM2,
∴△CFH的面积CF HM(22)×(2)=34,
故答案为:34.
8.解:过N作NH⊥AB于H,如图:
∵∠FHN=∠FAD=90°,
∴HN∥AD,
∴∠ADF=∠HNF,
设tan∠ADF=tan∠FNH=k,设NH=AH=b,则FH=kb,
∴AF=b+kb,
∵tan∠ADF,
∴ADb,
∴S2AF HNb2(1+k),S1=S△ADC﹣2S△ADN(b)2﹣2 b b,
∵S2=2S1,
∴b2(1+k)=2 [(b)2﹣2 b b],
整理得:k2+2k﹣2=0,
解得:k1或1(舍弃),
∴tan∠ADF=k1,
故答案为:1.
9.解:∵四边形ABCD是正方形,
∴AB=AD,∠BAF=∠ADE=90°.
∵CE=DF,
∴AF=DE.
在△ABF和△DAE中,
,
∴△ABF≌△DAE(SAS).
∴AE=BF,故①正确.
∵△ABF≌△DAE,
∴∠AFB=∠AED.
∵∠AED+∠DAE=90°,
∴∠AFB+∠DAE=90°,
∴∠AOF=90°,即AE⊥BF,故①正确.
∵△ABF≌△DAE,
∴S△ABF=S△ADE.
∴S△AOB=S△ABF﹣S△AOF,S四边形DEOF=S△ADE﹣S△AOF,即S△AOB=S四边形DEOF,故②正确.
如图过点E作EM⊥AB,交于点M,连接OM,
在正方形ABCD中,
∠BAD=∠ADE=∠AME=90°,
∴四边形ADEM为矩形,
AD=EM,
在△OME中,
∵∠EOM为钝角,
∴△EOM不是以点E为顶点的等腰△,
∴OE≠EM,
即AD≠OE,
故③错误.
如图,连接OC,延长AE使AE=EG,交BC延长线于点G,过点C作CH⊥AG交于点H,
∵E是边DC的中点,
∴ED=EC,
在△ADE和△GCE中,
,
∴△ADE≌△GCE(SAS),
所以∠ECG=∠EDA=90°=∠BCE,
∴点B、C、G共线,
∴∠G=∠GAD
设边AD=DC=2a,
∴AF=DE=a,
tan∠GAD,
∴tan∠CGA,
AEa,
∴AG=2AE=2a,
∵CG=AD,
∴CG=2a,
在△CEG中,CHa,HGa,
在△AOF中,AOa,
∴OH=AG﹣HG﹣AOa,
在Rt△CHO中,tan∠EOC,
故④正确.
故答案为:①②④.
10.解:如图,过点F作FM⊥AB于点M,
∵四边形ABCD为正方形,
∴∠A=∠ABC=90°,AB=BC,
∵FM⊥AB,
∴四边形MBCF为矩形,
∴MF=BC=AB,∠FME=90°,
由折叠可知,EF⊥BP,
∴∠PBE+∠BEF=90°,
∵∠PBE+∠APB=90°,
∴∠BEF=∠APB,即∠MEF=∠APB,
在△ABP和△MFE中,
,
∴△ABP≌△MFE(AAS),
∴BP=EF,故①正确;
由折叠可知,BE=PE,
设BE=PE=x,则AE=4﹣x,
∵P为AD中点,
∴AP=2,
在Rt△PAE中,AP2+AE2=PE2,
∴22+(4﹣x)2=x2,
解得:x,
∴AE=4﹣x,PE,
∴AE:AP:PE:2:3:4:5,
即△PAE三边之比为3:4:5,故②正确;
由折叠可知,BE=PE,∠EBC=∠EPG=90°,
∴∠PBE=∠BPE,∠BPE+∠BPH=90°,
∵∠PBE+∠APB=90°,
∴∠APB=∠BPH,故③正确;
如图,过点B作BN⊥PH于点N,
∴∠BAP=∠BNP=90°,
在△ABP和△NBP中,
,
∴△ABP≌△NBP(AAS),
∴AB=BN,AP=PN,
∴BC=BN,
在Rt△BNH和Rt△BCH中,
,
∴Rt△BNH≌Rt△BCH(HL),
∴NH=CH,
∴C△PDH=PD+PN+NH+DH=PD+AP+CH+DH=2AD=8,故④正确.
综上,正确的结论有①②③④.
故答案为:①②③④.
三.解答题
11.解:如图所示:
BP与AQ互相垂直且相等,理由如下:
∵四边形ABCD是正方形,
∴AB=AD=CD,∠BAP=∠ADQ=90°,
∵PD=QC,
∴AD﹣PD=CD﹣QC,即AP=DQ,
在△ABP和△DAQ中,
,
∴△ABP≌△DAQ(SAS),
∴BP=AQ,∠ABP=∠DAQ,
∵四边形ABCD是正方形,
∴AD∥BC,∠ABC=90°,
∴∠APB=∠PBC,
∵∠ABP+∠PBC=∠ABC=90°,
∴∠DAQ+∠APB=90°,
∵∴∠DAQ+∠APB+∠AOP=180°,
∴∠AOP=180°﹣(∠DAQ+∠APB)=90°,
∴BP⊥AQ,
∴BP与AQ互相垂直且相等.
12.解:AE与BF的位置关系是:垂直;大小关系是:相等.
证明:∵四边形ABCD为正方形,
∴AB=BC,∠ABC=∠BCD=90°,
又动点E,F分别从正方形ABCD的两个顶点B,C同时出发,以相同速度分别沿边BC和CD移动,
∴BE=CF,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(SAS),
∴∠EAB=∠FBC,AE=BF,
∵∠CBF+∠ABO=90°,
∴∠EAB+∠ABO=90°,
在△ABO中,∠AOB=180°﹣(∠EAB+∠ABO)=90°,
∴AE⊥BF.
13.解:(1)MN=AP.
证明:过点M作MG⊥CD于点G,则四边形AMGD是矩形,
∴MG=AD,∠MGN=90°,
∵四边形ABCD是正方形,
∴∠ABP=90°,AB=BC=AD,
∴MG=AB,∠ABP=∠MGN,
又∵MN⊥AP,
∴∠AEM=90°,
∴∠AME+∠BAP=90°,
又∵∠NMG+∠AME=90°,
∴∠NMG=∠BAP,
∴△ABP≌△MGN(ASA),
∴AP=MN;
(2)①补全图形如图2,
②如图3,过点P作PH∥AB交MN于点H,交BD于点K,过点M作MG⊥CD于点G,
∵AM∥PH,
∴∠MAE=∠EPH,
∵E为AP的中点,
∴AE=EP,
又∵∠AEM=∠PEH,
∴△AME≌△PHE(ASA),
∴ME=EH,AM=PH,
∵四边形AMGD是矩形,
∴AM=DG,
∴DG=PH,
∵∠CBD=45°,∠BPK=90°,
∴∠PBK=∠BKP=45°,
∴BP=PK,
由(1)知△ABP≌△MGN,
∴BP=NG,
∴PK=NG,
∴HK=DN,
又∵NK∥DN,
∴∠HKF=∠NDF,
∴△HKF≌△NDF(AAS),
∴HF=NF,
∴EF=EH+HF=EM+FN.
故答案为:EF=EM+FN.
14.解:(1)∵∠BAE=30°,
∴AE=2BE,
设BE=x,则AE=2x,
在Rt△ABE中,x2(2x)2,
解得x=2或﹣2(舍去),
∴AE=4;
(2)如图,过点B作BR∥GH,交CD于R,
∵GH∥BR,AB∥CD,
∴四边形BRHG是平行四边形,
∴GH=BR,∠BGH=∠BRH,
∵GH=AE,
∴BR=GH=AE.
又∵AB=BC,
∴Rt△ABE≌Rt△BCR(HL),
∴∠BAE=∠CBR=30°,
∴∠BRC=60°=∠AEB,
∴∠BRH=120°=∠BGH,
∴∠AGH=60°,
∴∠AFG=180°﹣60°﹣30°=90°,
∵∠BAE=30°,
∴AG=2GF,
∴AG2=GF2﹣AF2,
∴3GF2=4.
∴GF,
∴AG;
如图,过点A作AR∥GH,交CD于R,过点G作GO⊥AE于点O,
同理可证:△ABE≌△ADR,
∴∠DAR=∠BAE=30°,
∴∠EAR=30°,
∵AR∥GH,
∴∠RAF=∠AFG=30°,
∴∠BAE=∠AFG,
∴AG=GF,
∵GO⊥AF,
∴AO=FO=1,
∵∠BAE=30°,
∴AG=2GO,
∴AG2﹣GO2=AO2,
∴3GO2=1,
∴GO,
∴AG,
∴AG的长为或;
(3)如图,连接AO,过点O作OQ⊥AB于点Q,OP⊥BC于点P,
∵四边形ABCD是正方形,
∴∠ABD=∠CBD=45°,
∵OQ⊥AB,OP⊥BC,
∴OQ=OP,
∵MN⊥AE,AE=EF,
∴AO=OE,
∴∠OAE=∠OEA,
∵OA=OE,OQ=OP,
∴Rt△AOQ≌Rt△EOP(HL),
∴∠OAQ=∠OEP,
∵∠BEA+∠AEO+∠OEP=180°,
∴60°+∠AEO+∠OAE+30°=180°,
∴∠AEO=45°.
15.解:(1)∵AE⊥BF,
∴∠EMB=90°,
∴∠FBC+∠BEM=90°,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,
∴∠FBC+∠BFC=90°,
∴∠BEM=∠BFC,
在△ABE和△BCF中,
,
∴△ABE≌△BCF(AAS),
∴AE=BF.
故答案为:=;
(2)GE=BF,理由如下:
如图2,过点A作AN∥GE,交BF于点H,交BC于点N,
∴∠EMB=∠NHB=90°,
∴∠FBC+∠BNH=90°,
∵四边形ABCD是正方形,
∴AD∥BC,AB=BC,∠BAD=∠ABC=∠C=90°,
∵AD∥BC,AN∥GE,
∴四边形ANEG是平行四边形,
∴AN=EG,
∵∠C=90°,
∴∠FBC+∠BFC=90°,
∴∠BNH=∠BFC,
∴△ABN≌△BCF(AAS),
∴AN=BF,
∵AN=EG,
∴GE=BF.
(3)①如图3,连接CH,
由(2)的结论可知,AE=MN,
∵四边形ABCD是正方形,BD是正方形的对角线,
∴∠ABD=∠CBD=45°,AB=BC,
∵BH=BH,
∴△ABH≌△CBH(SAS),
∴∠BAH=∠BCH,AH=CH,
由折叠可知,AH=AH′,NH=NH′,
∵∠ABN+∠AHN=180°,
∴∠BAH+∠BNH=180°,
∵∠BNH+∠HNC=180°,
∴∠BAH=∠HNC,
∴∠HNC=∠NCH,
∴NH=CH,
∴NH=CH=AH=AH′=NH′,
∴四边形AHNH′是菱形,
∵∠AHN=90°,
∴菱形AHNH′是正方形;
②如图4,作H′Q⊥BC交CB的延长线于点Q,作HF⊥BC于点M,
∴∠H′QN=∠HFB=90°,
由上知四边形AHNH′是正方形,
∴H′N=HN,∠H′NH=90°,AH′AN,
∴∠H′NQ+∠HNF=∠HNF+∠NHF=90°,
∴∠H′NQ=∠NHF,
∴△H′QN≌△NFH′(AAS),
∴H′Q=NF,QN=HF;
∵∠HBF=45°,∠HFB=90°,
∴△BHF是等腰直角三角形,
∴HF=BF=NF+BN,
∵QN=QB+BN,
∴NF=QB=QH′,
∴∠H′BQ=∠ABH′=45°,
∴∠H′BD=90°;
如图4,作P关于BH′的对称点P′,则PH′=P′H′,过点P′作PK⊥AB交AB延长线于点K,
则△PBK是等腰直角三角形,
∴PH′AN=PH′+AH′=P′H′+AH′≥AP′,即当A,H′,P′三点共线时,PH′AN最小,最小值为AP′的长.
∵AB=6,
∴BD=6,
∵BD=3BP,
∴BP=BP′=2,
∴PK=BK=2,
∴AK=8,
∴AP′2,即PH′AN的最小值为2.
故答案为:2.
16.
解:(1)选命题①
在图1中,∵△ABC是正三角形,
∴BC=CA,∠BCM=∠CAN=60°.
∵∠BON=60°,
∴∠CBM+∠BCN=60°.
∵∠BCN+∠ACN=60°,
∴∠CBM=∠ACN.
∴△BCM≌△CAN(ASA).
∴BM=CN.
选命题②
在图2中∵四边形ABCD是正方形,
∴BC=CD,∠BCM=∠CDN=90°.
∵∠BON=90°,
∴∠CBM+∠BCN=90°.
∵∠BCN+∠DCN=90°,
∴∠CBM=∠DCN.
∴△BCM≌△CDN(ASA).
∴BM=CN.
选命题③
在图3中,∵五边形ABCDE是正五边形,
∴BC=CD,∠BCM=∠CDN=108°.
∵∠BON=108°,
∴∠CBM+∠BCN=108°.
∵∠BCN+∠DCN=108°,
∴∠CBM=∠DCN.
∴△BCM≌△CDN(ASA).
∴BM=CN.
(2)①当∠BON时,结论BM=CN成立.
②BM=CN成立.
在图5中,连接BD、CE,
∵五边形ABCDE是正五边形,
∴BC=CD,∠BCD=∠CDE=108°,CD=DE,∠CDE=∠DEA=108°.
∴∠BCD=∠DEA,
∴△BCD≌△CDE(SAS).
∴BD=CE,∠BDC=∠CED,∠DBC=∠ECD.
∵∠BON=108°,
∴∠OBC+∠OCB=108°.
∵∠OCB+∠OCD=108°,
∴∠OBC=∠OCD(即∠MBC=∠NCD).
∴∠MBC﹣∠DBC=∠NCD﹣∠ECD,即∠DBM=∠ECN.
∴∠CDE﹣∠BDC=∠DEA﹣∠CED,即∠BDM=∠CEN.
∴△BDM≌△CEN(ASA).
∴BM=CN.
同课章节目录
