2025年中考数学九年级一轮复习【数据与概率】专题(抽样与数据分析部分)过关题(含答案)
文档属性
| 名称 | 2025年中考数学九年级一轮复习【数据与概率】专题(抽样与数据分析部分)过关题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 309.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 17:47:01 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年中考数学九年级
一轮复习【数据与概率】专题(抽样与数据分析)部分过关题
一、单选题
1.(2024八下·宿迁月考)为了了解某校八年级1 000名学生的身高,从中抽取了50名学生并对他们的身高进行统计分析,在这个问题中,总体是指( )
A.1 000名学生 B.被抽取的50名学生
C.1 000名学生的身高 D.被抽取的50名学生的身高
2.(2019·安阳模拟)瑞安市10月份第一周每天最低气温(℃)分别为:19,19,22,24,19,20,24,则这一周最低气温的中位数是( )
A.22 B.19 C.24 D.20
3.(2024九下·龙华月考)2023年2月,某区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )
A.32,31 B.31,32 C.31,34 D.31,31
4.(2023九上·苏州月考)九(1)班45名同学一周课外阅读时间统计如表所示,那么该班45名同学一周课外阅读时间的众数、中位数分别是( )
人数(人) 5 19 15 6
时间(小时) 6 7 9 10
A.7,7 B.19,8 C.10,7 D.7,8
5.(2024七下·海兴期末)下列调查中,适宜采用全面调查方式的是( )
A.检测“神舟十四号”载人飞船零件的质量
B.检测一批LED灯的使用寿命
C.检测黄冈、孝感、咸宁三市的空气质量
D.检测一批家用汽车的抗撞击能力
6.(2017·淳安模拟)甲、乙、丙、丁四位运动员在“110米栏”训练中,每人各跑5次,据统计,平均成绩都是13.2秒,方差分别是S甲2=0.11,S乙2=0.03,S丙2=0.05,S丁2=0.02,则这四位运动员“110米栏”的训练成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
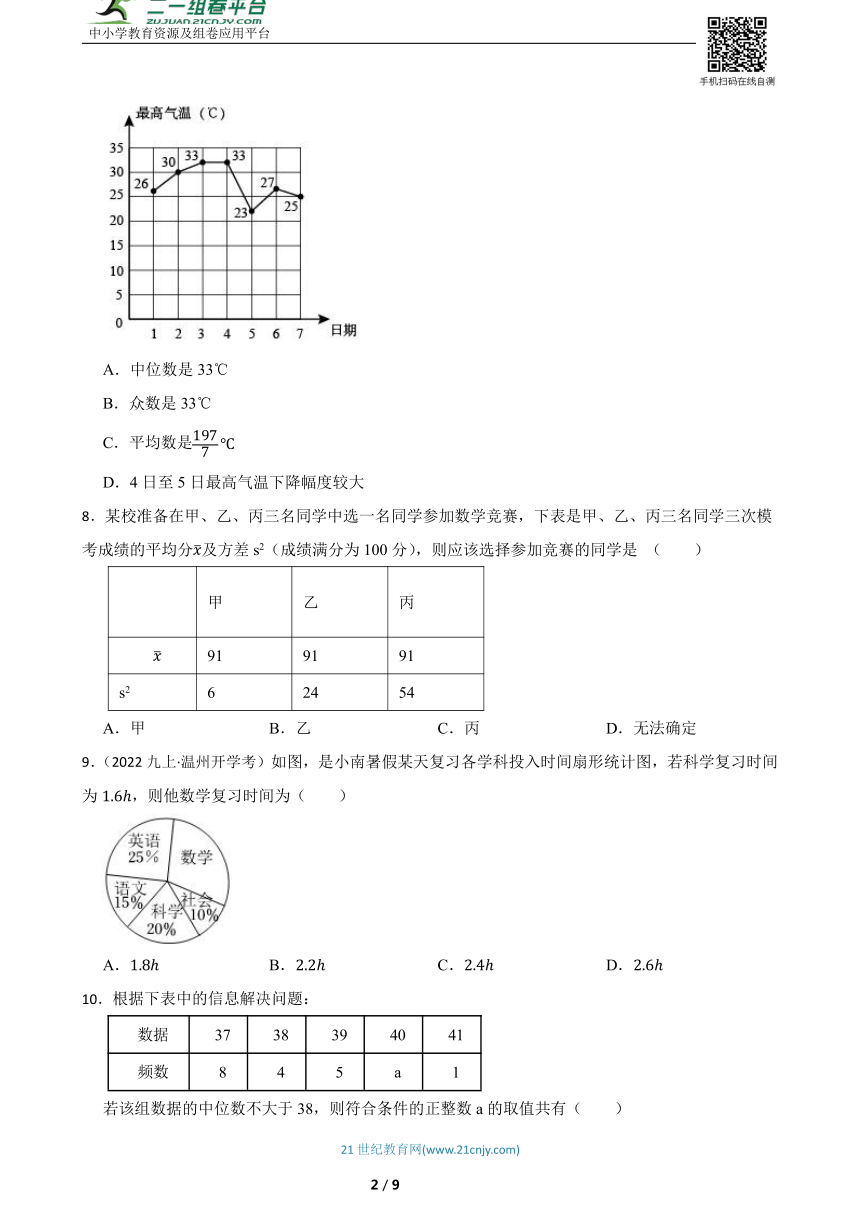
7.(2022·鄄城模拟)小茗同学对5月1日至7日的最高气温进行统计分析制作成统计图(如图所示),下列说法错误的是( )
A.中位数是33℃
B.众数是33℃
C.平均数是
D.4日至5日最高气温下降幅度较大
8.某校准备在甲、乙、丙三名同学中选一名同学参加数学竞赛,下表是甲、乙、丙三名同学三次模考成绩的平均分及方差s2(成绩满分为100分),则应该选择参加竞赛的同学是 ( )
甲 乙 丙
91 91 91
s2 6 24 54
A.甲 B.乙 C.丙 D.无法确定
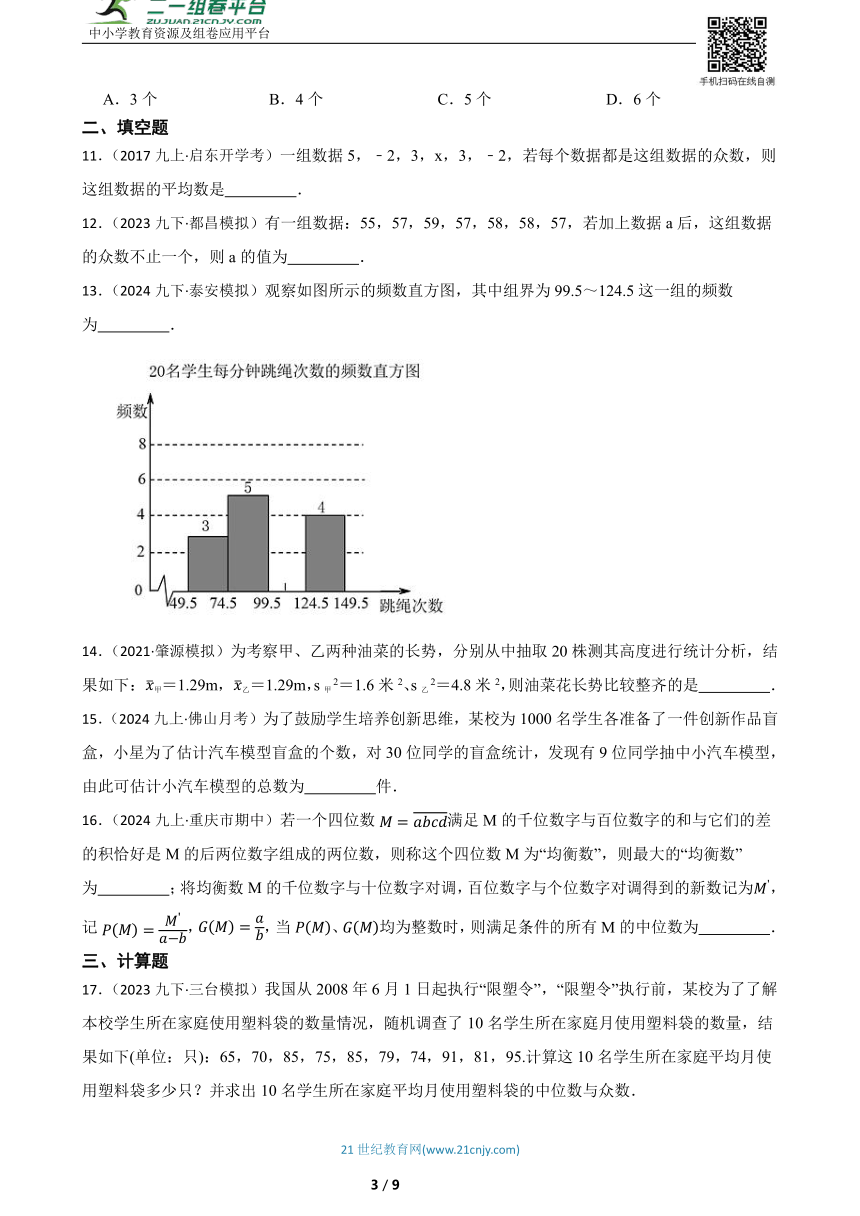
9.(2022九上·温州开学考)如图,是小南暑假某天复习各学科投入时间扇形统计图,若科学复习时间为,则他数学复习时间为( )
A. B. C. D.
10.根据下表中的信息解决问题:
数据 37 38 39 40 41
频数 8 4 5 a 1
若该组数据的中位数不大于38,则符合条件的正整数a的取值共有( )
A.3个 B.4个 C.5个 D.6个
二、填空题
11.(2017九上·启东开学考)一组数据5,﹣2,3,x,3,﹣2,若每个数据都是这组数据的众数,则这组数据的平均数是 .
12.(2023九下·都昌模拟)有一组数据:55,57,59,57,58,58,57,若加上数据a后,这组数据的众数不止一个,则a的值为 .
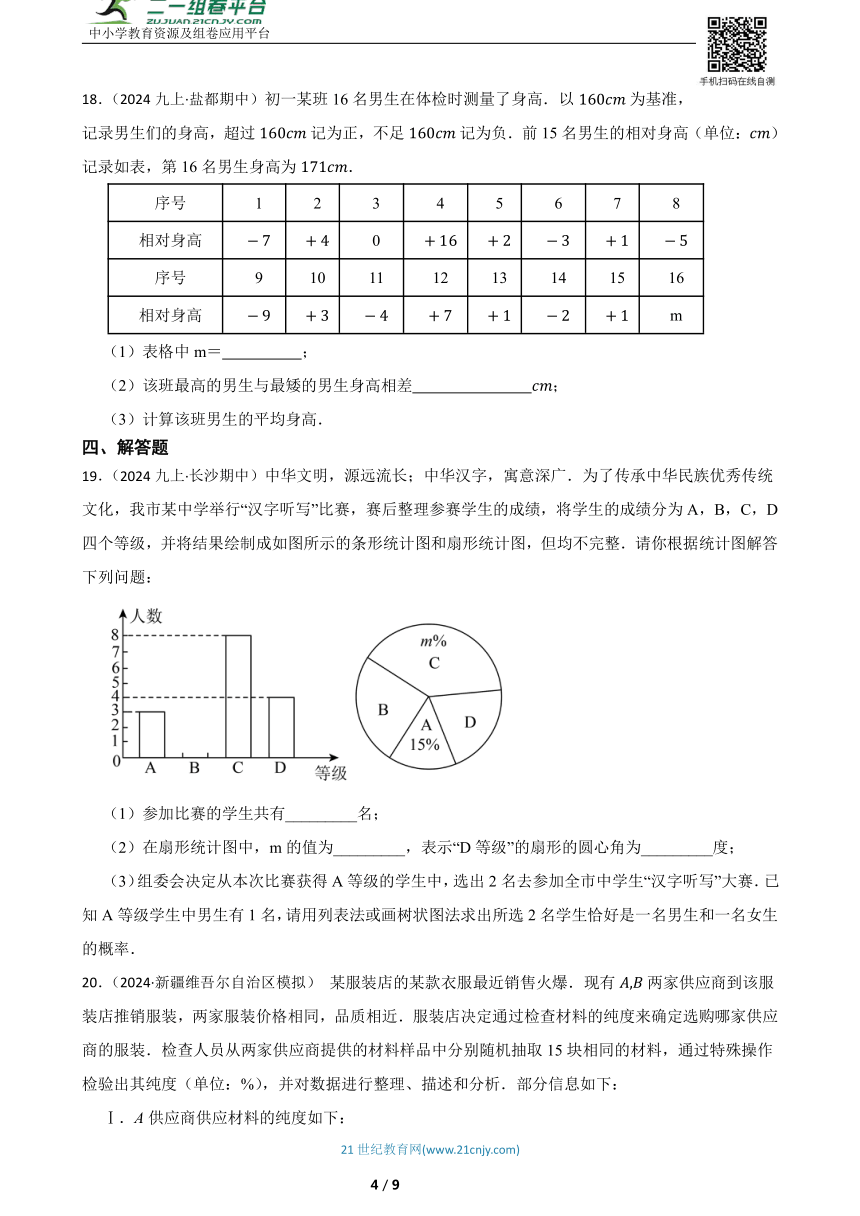
13.(2024九下·泰安模拟)观察如图所示的频数直方图,其中组界为99.5~124.5这一组的频数为 .
14.(2021·肇源模拟)为考察甲、乙两种油菜的长势,分别从中抽取20株测其高度进行统计分析,结果如下: 甲=1.29m, 乙=1.29m,s甲2=1.6米2、s乙2=4.8米2,则油菜花长势比较整齐的是 .
15.(2024九上·佛山月考)为了鼓励学生培养创新思维,某校为1000名学生各准备了一件创新作品盲盒,小星为了估计汽车模型盲盒的个数,对30位同学的盲盒统计,发现有9位同学抽中小汽车模型,由此可估计小汽车模型的总数为 件.
16.(2024九上·重庆市期中)若一个四位数满足M的千位数字与百位数字的和与它们的差的积恰好是M的后两位数字组成的两位数,则称这个四位数M为“均衡数”,则最大的“均衡数”为 ;将均衡数M的千位数字与十位数字对调,百位数字与个位数字对调得到的新数记为,记,,当、均为整数时,则满足条件的所有M的中位数为 .
三、计算题
17.(2023九下·三台模拟)我国从2008年6月1日起执行“限塑令”,“限塑令”执行前,某校为了了解本校学生所在家庭使用塑料袋的数量情况,随机调查了10名学生所在家庭月使用塑料袋的数量,结果如下(单位:只):65,70,85,75,85,79,74,91,81,95.计算这10名学生所在家庭平均月使用塑料袋多少只?并求出10名学生所在家庭平均月使用塑料袋的中位数与众数.
18.(2024九上·盐都期中)初一某班16名男生在体检时测量了身高.以为基准,记录男生们的身高,超过记为正,不足记为负.前15名男生的相对身高(单位:)记录如表,第16名男生身高为.
序号 1 2 3 4 5 6 7 8
相对身高 0
序号 9 10 11 12 13 14 15 16
相对身高 m
(1)表格中m= ;
(2)该班最高的男生与最矮的男生身高相差 ;
(3)计算该班男生的平均身高.
四、解答题
19.(2024九上·长沙期中)中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.请你根据统计图解答下列问题:
(1)参加比赛的学生共有_________名;
(2)在扇形统计图中,m的值为_________,表示“D等级”的扇形的圆心角为_________度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
20.(2024·新疆维吾尔自治区模拟) 某服装店的某款衣服最近销售火爆.现有两家供应商到该服装店推销服装,两家服装价格相同,品质相近.服装店决定通过检查材料的纯度来确定选购哪家供应商的服装.检查人员从两家供应商提供的材料样品中分别随机抽取15块相同的材料,通过特殊操作检验出其纯度(单位:%),并对数据进行整理、描述和分析.部分信息如下:
Ⅰ.A供应商供应材料的纯度如下:
A 72 73 74 75 76 78 79
频数 1 1 5 3 3 1 1
Ⅱ.B供应商供应材料的纯度如下:
Ⅲ.A,B两家供应商供应材料纯度的平均数、中位数、众数和方差如下:
平均数 中位数 众数 方差
A 75 75 74 3.07
B 75
根据以上信息,回答下列问题:
(1)表格中的 , , ;
(2)你认为服装店应选择哪家供应商供应服装?为什么?
21.为了了解某班20名同学甲、乙两门课程的学习情况,分别对其测试后的成绩统计并整理如下:
①20名同学甲课程的成绩(单位:分):
61,65,68,71,72,72,73,73,73,73,
75,78,82,84,86,86,88,90,93,98.
②20名同学乙课程成绩的频数直方图(每一组包含前一个边界值,不包含后一个边界值)如图.
根据以上信息,回答下列问题:
(1)甲课程成绩的众数是 分,中位数是 分.
(2)依次记左边50~60的分数段为第一组,90~100的分数段为第五组,则乙课程成绩的中位数在第 组内.
(3)在此次测试中,小聪同学甲课程成绩为75分,乙课程成绩为78分,他的 (填“甲”或“乙”)课程的成绩排名更靠前.
22.某校为了解本校学生对自己视力保护的重视程度, 随机在校内调查了部分学生, 调查结果分为“非常重视” “重视” “比较重视” “不重视” 四类,并将结果绘制成下图所示的两幅不完整的统计图. 根据图中信息,解答下列问题:
(1)在扇形统计图中, “比较重视”所占的圆心角的度数为 ,并补全条形统计图.
(2)该校共有学生 2400 人, 请你估计该校对视力保护“非常重视”的学生人数.
(3)对视力 “非常重视” 的 4 人有一名男生、三名女生, 若从中随机抽取两人向全校作视力保护经验交流, 请利用树状图或列表法, 求出恰好抽到的都是女生的概率.
答案解析部分
1.【答案】C
【知识点】总体、个体、样本、样本容量
2.【答案】D
【知识点】中位数
3.【答案】D
【知识点】中位数;众数
4.【答案】A
【知识点】中位数;众数
5.【答案】A
【知识点】全面调查与抽样调查
6.【答案】D
【知识点】方差
7.【答案】A
【知识点】折线统计图;分析数据的集中趋势(平均数、中位数、众数)
8.【答案】A
【知识点】平均数及其计算;方差
9.【答案】C
【知识点】扇形统计图
10.【答案】C
【知识点】平均数及其计算
11.【答案】2
【知识点】平均数及其计算
12.【答案】58
【知识点】众数
13.【答案】8
【知识点】频数(率)分布直方图
14.【答案】甲
【知识点】方差
15.【答案】300
【知识点】用样本估计总体
16.【答案】9817;6327
【知识点】中位数
17.【答案】这10名学生所在家庭平均月使用塑料袋80只; 平均月使用塑料袋的中位数与众数为80、85.
【知识点】平均数及其计算;中位数;众数
18.【答案】(1)
(2)25
(3)
【知识点】平均数及其计算;正数、负数的实际应用
19.【答案】(1)20
(2)40,72
(3)
【知识点】扇形统计图;用列表法或树状图法求概率
20.【答案】(1)75;75;6
(2)选A供应商供应服装,理由如下:
平均值一样,B的方差比A的大,A更稳定,
选A供应商供应服装.
【知识点】中位数;方差;众数
21.【答案】(1)73;74
(2)四
(3)甲
【知识点】频数(率)分布直方图;中位数;众数
22.【答案】(1)解:24; 补全的条形统计图如下.
(2)解:由题意得, (人),
估计该校对视力保护 “非常重视”的学生有 120 人.
(3)解:画树状图如下,
共有 12 种等可能的结果, 抽到都是女生的有 6 种,
佮好抽到的都是女生的概率为 .
【知识点】用列表法或树状图法求概率;简单事件概率的计算;用样本所占百分比估计总体数量
21世纪教育网(www.21cnjy.com)
1 / 9
2025年中考数学九年级
一轮复习【数据与概率】专题(抽样与数据分析)部分过关题
一、单选题
1.(2024八下·宿迁月考)为了了解某校八年级1 000名学生的身高,从中抽取了50名学生并对他们的身高进行统计分析,在这个问题中,总体是指( )
A.1 000名学生 B.被抽取的50名学生
C.1 000名学生的身高 D.被抽取的50名学生的身高
2.(2019·安阳模拟)瑞安市10月份第一周每天最低气温(℃)分别为:19,19,22,24,19,20,24,则这一周最低气温的中位数是( )
A.22 B.19 C.24 D.20
3.(2024九下·龙华月考)2023年2月,某区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )
A.32,31 B.31,32 C.31,34 D.31,31
4.(2023九上·苏州月考)九(1)班45名同学一周课外阅读时间统计如表所示,那么该班45名同学一周课外阅读时间的众数、中位数分别是( )
人数(人) 5 19 15 6
时间(小时) 6 7 9 10
A.7,7 B.19,8 C.10,7 D.7,8
5.(2024七下·海兴期末)下列调查中,适宜采用全面调查方式的是( )
A.检测“神舟十四号”载人飞船零件的质量
B.检测一批LED灯的使用寿命
C.检测黄冈、孝感、咸宁三市的空气质量
D.检测一批家用汽车的抗撞击能力
6.(2017·淳安模拟)甲、乙、丙、丁四位运动员在“110米栏”训练中,每人各跑5次,据统计,平均成绩都是13.2秒,方差分别是S甲2=0.11,S乙2=0.03,S丙2=0.05,S丁2=0.02,则这四位运动员“110米栏”的训练成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
7.(2022·鄄城模拟)小茗同学对5月1日至7日的最高气温进行统计分析制作成统计图(如图所示),下列说法错误的是( )
A.中位数是33℃
B.众数是33℃
C.平均数是
D.4日至5日最高气温下降幅度较大
8.某校准备在甲、乙、丙三名同学中选一名同学参加数学竞赛,下表是甲、乙、丙三名同学三次模考成绩的平均分及方差s2(成绩满分为100分),则应该选择参加竞赛的同学是 ( )
甲 乙 丙
91 91 91
s2 6 24 54
A.甲 B.乙 C.丙 D.无法确定
9.(2022九上·温州开学考)如图,是小南暑假某天复习各学科投入时间扇形统计图,若科学复习时间为,则他数学复习时间为( )
A. B. C. D.
10.根据下表中的信息解决问题:
数据 37 38 39 40 41
频数 8 4 5 a 1
若该组数据的中位数不大于38,则符合条件的正整数a的取值共有( )
A.3个 B.4个 C.5个 D.6个
二、填空题
11.(2017九上·启东开学考)一组数据5,﹣2,3,x,3,﹣2,若每个数据都是这组数据的众数,则这组数据的平均数是 .
12.(2023九下·都昌模拟)有一组数据:55,57,59,57,58,58,57,若加上数据a后,这组数据的众数不止一个,则a的值为 .
13.(2024九下·泰安模拟)观察如图所示的频数直方图,其中组界为99.5~124.5这一组的频数为 .
14.(2021·肇源模拟)为考察甲、乙两种油菜的长势,分别从中抽取20株测其高度进行统计分析,结果如下: 甲=1.29m, 乙=1.29m,s甲2=1.6米2、s乙2=4.8米2,则油菜花长势比较整齐的是 .
15.(2024九上·佛山月考)为了鼓励学生培养创新思维,某校为1000名学生各准备了一件创新作品盲盒,小星为了估计汽车模型盲盒的个数,对30位同学的盲盒统计,发现有9位同学抽中小汽车模型,由此可估计小汽车模型的总数为 件.
16.(2024九上·重庆市期中)若一个四位数满足M的千位数字与百位数字的和与它们的差的积恰好是M的后两位数字组成的两位数,则称这个四位数M为“均衡数”,则最大的“均衡数”为 ;将均衡数M的千位数字与十位数字对调,百位数字与个位数字对调得到的新数记为,记,,当、均为整数时,则满足条件的所有M的中位数为 .
三、计算题
17.(2023九下·三台模拟)我国从2008年6月1日起执行“限塑令”,“限塑令”执行前,某校为了了解本校学生所在家庭使用塑料袋的数量情况,随机调查了10名学生所在家庭月使用塑料袋的数量,结果如下(单位:只):65,70,85,75,85,79,74,91,81,95.计算这10名学生所在家庭平均月使用塑料袋多少只?并求出10名学生所在家庭平均月使用塑料袋的中位数与众数.
18.(2024九上·盐都期中)初一某班16名男生在体检时测量了身高.以为基准,记录男生们的身高,超过记为正,不足记为负.前15名男生的相对身高(单位:)记录如表,第16名男生身高为.
序号 1 2 3 4 5 6 7 8
相对身高 0
序号 9 10 11 12 13 14 15 16
相对身高 m
(1)表格中m= ;
(2)该班最高的男生与最矮的男生身高相差 ;
(3)计算该班男生的平均身高.
四、解答题
19.(2024九上·长沙期中)中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.请你根据统计图解答下列问题:
(1)参加比赛的学生共有_________名;
(2)在扇形统计图中,m的值为_________,表示“D等级”的扇形的圆心角为_________度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
20.(2024·新疆维吾尔自治区模拟) 某服装店的某款衣服最近销售火爆.现有两家供应商到该服装店推销服装,两家服装价格相同,品质相近.服装店决定通过检查材料的纯度来确定选购哪家供应商的服装.检查人员从两家供应商提供的材料样品中分别随机抽取15块相同的材料,通过特殊操作检验出其纯度(单位:%),并对数据进行整理、描述和分析.部分信息如下:
Ⅰ.A供应商供应材料的纯度如下:
A 72 73 74 75 76 78 79
频数 1 1 5 3 3 1 1
Ⅱ.B供应商供应材料的纯度如下:
Ⅲ.A,B两家供应商供应材料纯度的平均数、中位数、众数和方差如下:
平均数 中位数 众数 方差
A 75 75 74 3.07
B 75
根据以上信息,回答下列问题:
(1)表格中的 , , ;
(2)你认为服装店应选择哪家供应商供应服装?为什么?
21.为了了解某班20名同学甲、乙两门课程的学习情况,分别对其测试后的成绩统计并整理如下:
①20名同学甲课程的成绩(单位:分):
61,65,68,71,72,72,73,73,73,73,
75,78,82,84,86,86,88,90,93,98.
②20名同学乙课程成绩的频数直方图(每一组包含前一个边界值,不包含后一个边界值)如图.
根据以上信息,回答下列问题:
(1)甲课程成绩的众数是 分,中位数是 分.
(2)依次记左边50~60的分数段为第一组,90~100的分数段为第五组,则乙课程成绩的中位数在第 组内.
(3)在此次测试中,小聪同学甲课程成绩为75分,乙课程成绩为78分,他的 (填“甲”或“乙”)课程的成绩排名更靠前.
22.某校为了解本校学生对自己视力保护的重视程度, 随机在校内调查了部分学生, 调查结果分为“非常重视” “重视” “比较重视” “不重视” 四类,并将结果绘制成下图所示的两幅不完整的统计图. 根据图中信息,解答下列问题:
(1)在扇形统计图中, “比较重视”所占的圆心角的度数为 ,并补全条形统计图.
(2)该校共有学生 2400 人, 请你估计该校对视力保护“非常重视”的学生人数.
(3)对视力 “非常重视” 的 4 人有一名男生、三名女生, 若从中随机抽取两人向全校作视力保护经验交流, 请利用树状图或列表法, 求出恰好抽到的都是女生的概率.
答案解析部分
1.【答案】C
【知识点】总体、个体、样本、样本容量
2.【答案】D
【知识点】中位数
3.【答案】D
【知识点】中位数;众数
4.【答案】A
【知识点】中位数;众数
5.【答案】A
【知识点】全面调查与抽样调查
6.【答案】D
【知识点】方差
7.【答案】A
【知识点】折线统计图;分析数据的集中趋势(平均数、中位数、众数)
8.【答案】A
【知识点】平均数及其计算;方差
9.【答案】C
【知识点】扇形统计图
10.【答案】C
【知识点】平均数及其计算
11.【答案】2
【知识点】平均数及其计算
12.【答案】58
【知识点】众数
13.【答案】8
【知识点】频数(率)分布直方图
14.【答案】甲
【知识点】方差
15.【答案】300
【知识点】用样本估计总体
16.【答案】9817;6327
【知识点】中位数
17.【答案】这10名学生所在家庭平均月使用塑料袋80只; 平均月使用塑料袋的中位数与众数为80、85.
【知识点】平均数及其计算;中位数;众数
18.【答案】(1)
(2)25
(3)
【知识点】平均数及其计算;正数、负数的实际应用
19.【答案】(1)20
(2)40,72
(3)
【知识点】扇形统计图;用列表法或树状图法求概率
20.【答案】(1)75;75;6
(2)选A供应商供应服装,理由如下:
平均值一样,B的方差比A的大,A更稳定,
选A供应商供应服装.
【知识点】中位数;方差;众数
21.【答案】(1)73;74
(2)四
(3)甲
【知识点】频数(率)分布直方图;中位数;众数
22.【答案】(1)解:24; 补全的条形统计图如下.
(2)解:由题意得, (人),
估计该校对视力保护 “非常重视”的学生有 120 人.
(3)解:画树状图如下,
共有 12 种等可能的结果, 抽到都是女生的有 6 种,
佮好抽到的都是女生的概率为 .
【知识点】用列表法或树状图法求概率;简单事件概率的计算;用样本所占百分比估计总体数量
21世纪教育网(www.21cnjy.com)
1 / 9
同课章节目录
