2025年九年级数学一轮复习【解题模型】专辑一(含答案)
文档属性
| 名称 | 2025年九年级数学一轮复习【解题模型】专辑一(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 655.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 14:56:21 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2025年九年级数学一轮复习【解题模型】专辑一
一、单选题
1.(2024九下·重庆市模拟)下列图形都是由边长相等且面积为1的等边三角形按一定的规律组成,其中,第①个图形面积为1,第②个图形面积为4,第③个图形面积为9,…,则第⑩个图形中三角形的个数是( )
A.81 B.100 C.99 D.101
2.(2024九上·金堂月考) 如图所示,一场台风过后,垂直于地面的一棵树在距地面1米处折断,树尖B 恰好碰到地面,经测量AB=2,则树高为( )米.
A.1+ B.1+ C.2-1 D.3
3.(2021九上·和平期末)顺次连接对角线互相垂直的四边形的各边中点,所形成的新四边形是( )
A.菱形 B.矩形 C.正方形 D.三角形
4.(2023·容县模拟)我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2×i=(﹣1)×i=﹣i,i4=(i2)2=(﹣1)2=1,从而对任意正整数n,我们可以得到i4n+1=i4n×i=(i4)n×i=i,i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+…+i2023的值为( )
A.0 B.1 C.﹣1 D.i
5.(2019九上·永登期中)如果顺次连接一个四边形各边中点所得新的四边形是菱形,那么对这个四边形的形状描述最准确的是( )
A.矩形 B.等腰梯形
C.菱形 D.对角线相等的四边形
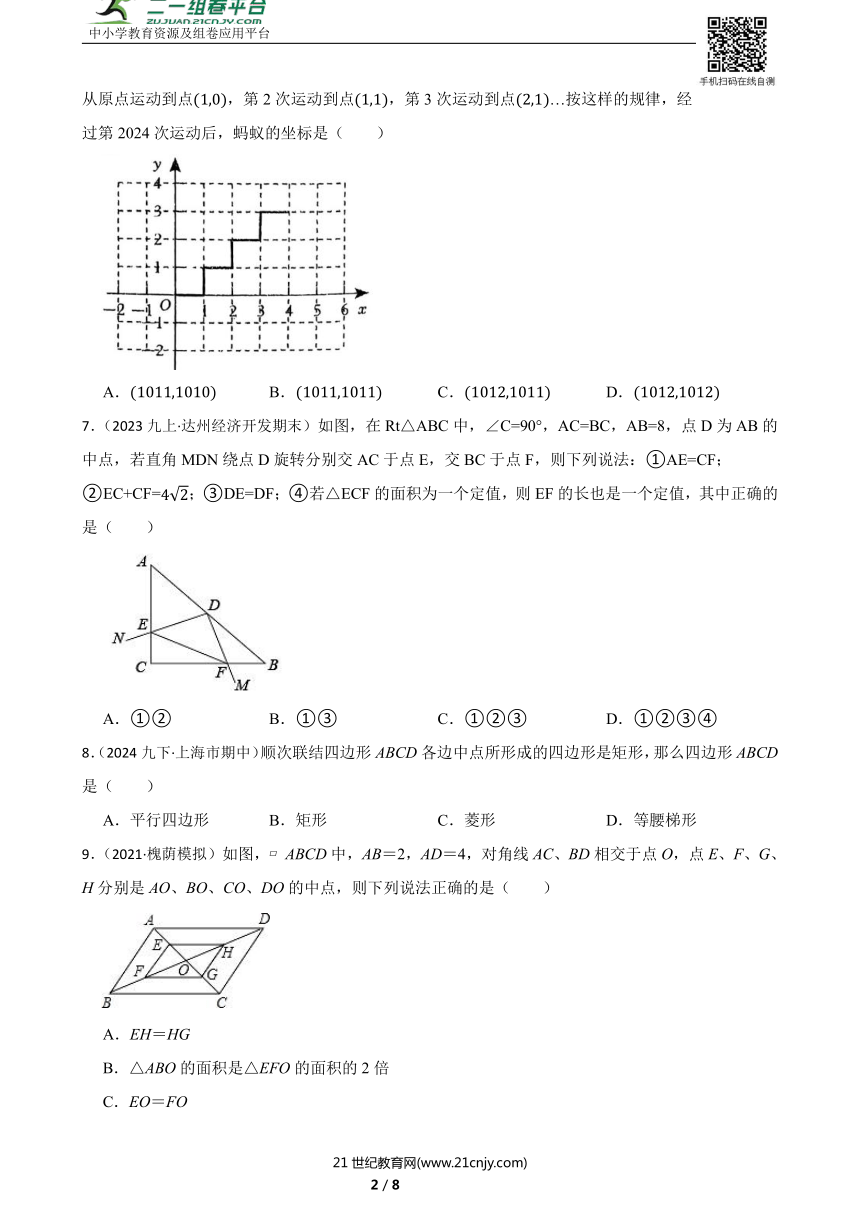
6.(2024·裕华模拟)如图,一只小蚂蚁在平面直角坐标系中按图中路线进行“爬楼梯”运动,第1次它从原点运动到点,第2次运动到点,第3次运动到点…按这样的规律,经过第2024次运动后,蚂蚁的坐标是( )
A. B. C. D.
7.(2023九上·达州经济开发期末)如图,在Rt△ABC中,∠C=90°,AC=BC,AB=8,点D为AB的中点,若直角MDN绕点D旋转分别交AC于点E,交BC于点F,则下列说法:①AE=CF;②EC+CF=;③DE=DF;④若△ECF的面积为一个定值,则EF的长也是一个定值,其中正确的是( )
A.①② B.①③ C.①②③ D.①②③④
8.(2024九下·上海市期中)顺次联结四边形ABCD各边中点所形成的四边形是矩形,那么四边形ABCD是( )
A.平行四边形 B.矩形 C.菱形 D.等腰梯形
9.(2021·槐荫模拟)如图, ABCD中,AB=2,AD=4,对角线AC、BD相交于点O,点E、F、G、H分别是AO、BO、CO、DO的中点,则下列说法正确的是( )
A.EH=HG
B.△ABO的面积是△EFO的面积的2倍
C.EO=FO
D.四边形EFGH是平行四边形
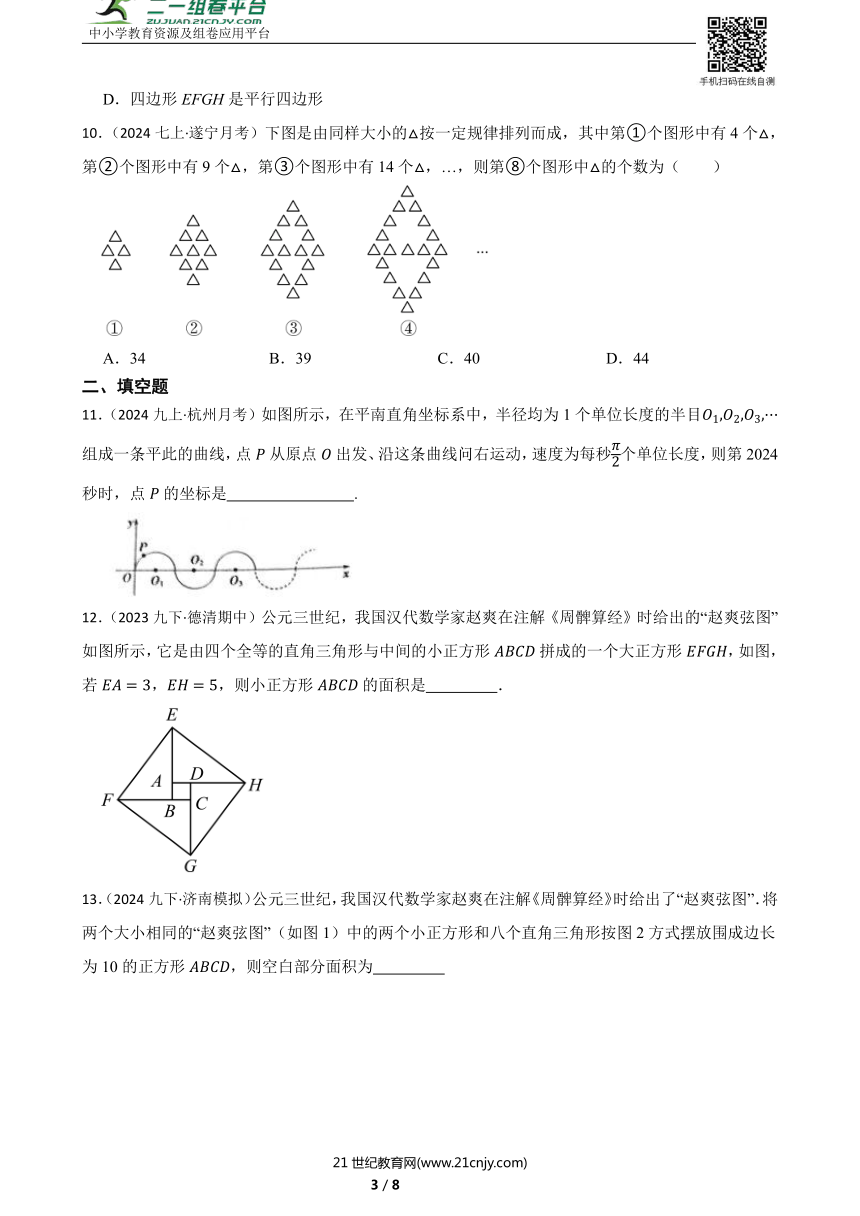
10.(2024七上·遂宁月考)下图是由同样大小的按一定规律排列而成,其中第①个图形中有4个,第②个图形中有9个,第③个图形中有14个,…,则第⑧个图形中的个数为( )
A.34 B.39 C.40 D.44
二、填空题
11.(2024九上·杭州月考)如图所示,在平南直角坐标系中,半径均为1个单位长度的半目组成一条平此的曲线,点从原点出发、沿这条曲线问右运动,速度为每秒个单位长度,则第2024秒时,点的坐标是 .
12.(2023九下·德清期中)公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如图,若,,则小正方形的面积是 .
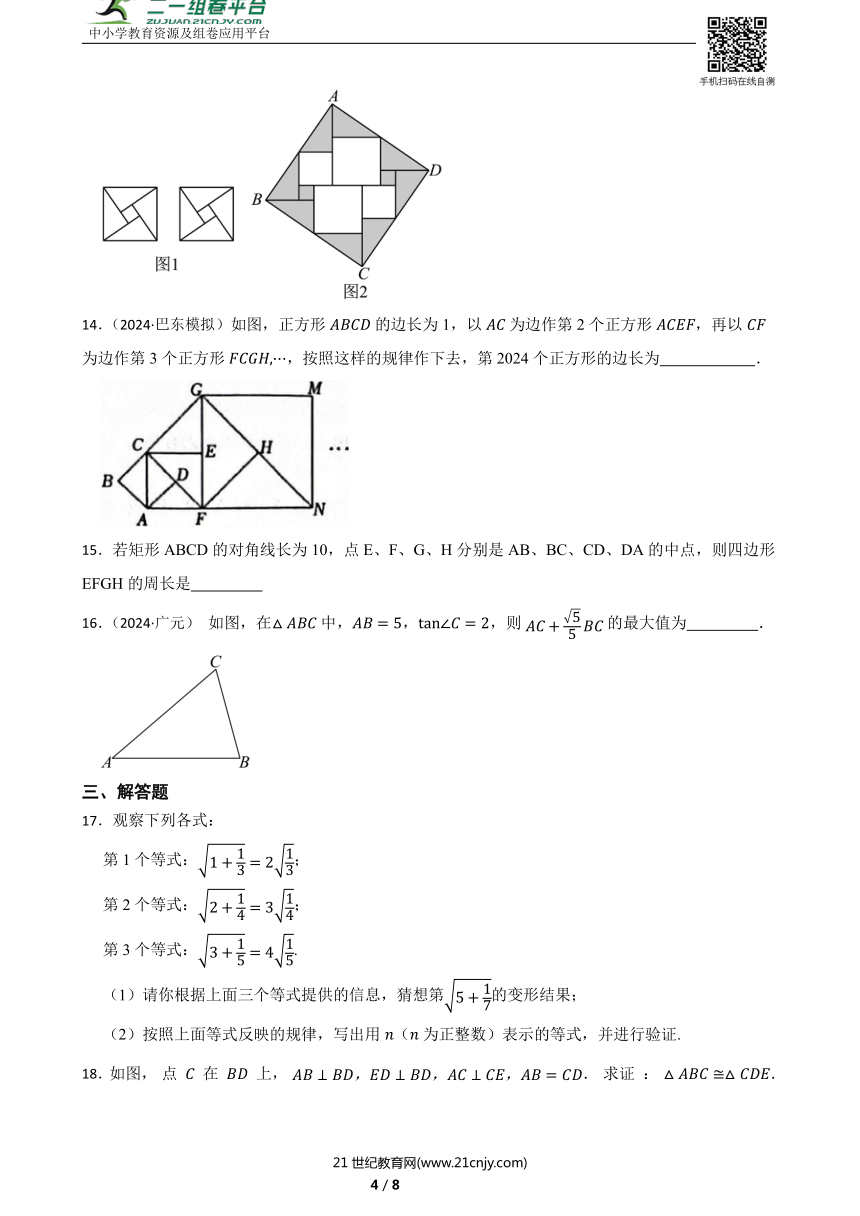
13.(2024九下·济南模拟)公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出了“赵爽弦图”.将两个大小相同的“赵爽弦图”(如图1)中的两个小正方形和八个直角三角形按图2方式摆放围成边长为10的正方形,则空白部分面积为
14.(2024·巴东模拟)如图,正方形的边长为1,以为边作第2个正方形,再以为边作第3个正方形,按照这样的规律作下去,第2024个正方形的边长为 .
15.若矩形ABCD的对角线长为10,点E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长是
16.(2024·广元) 如图,在中,,,则的最大值为 .
三、解答题
17.观察下列各式:
第1个等式:;
第2个等式:;
第3个等式:.
(1)请你根据上面三个等式提供的信息,猜想第的变形结果;
(2)按照上面等式反映的规律,写出用(为正整数)表示的等式,并进行验证.
18.如图, 点 在 上, . 求证 : .
19.用灰白两种颜色的正方形地砖, 按如图 所示的规律拼成图案:
(1)第 4 个图案有白色地砖多少块? 第 个图案呢?
(2)已知每个小正方形的边长均为 , 若学校用第 个图案铺设长为 的长廊,则需要灰色地砖多少块?
20.如图,在矩形 中, 是 边的中点, 是线段 边上的动点, 将 沿 所在的直线折叠得到 , 连结 , 求 的最小值.
答案解析部分
1.【答案】B
【知识点】探索规律-图形的递变规律
2.【答案】A
【知识点】风吹树折模型
3.【答案】B
【知识点】中点四边形模型
4.【答案】C
【知识点】探索规律-等式类规律
5.【答案】D
【知识点】中点四边形模型
6.【答案】D
【知识点】探索规律-点的坐标规律
7.【答案】D
【知识点】旋转全等模型
8.【答案】C
【知识点】中点四边形模型
9.【答案】D
【知识点】中点四边形模型
10.【答案】B
【知识点】探索规律-图形的个数规律;探索规律-图形的递变规律
11.【答案】(2024,0)
【知识点】探索规律-点的坐标规律
12.【答案】1
【知识点】“赵爽弦图”模型
13.【答案】50
【知识点】“赵爽弦图”模型
14.【答案】
【知识点】探索规律-图形的递变规律
15.【答案】20
【知识点】中点四边形模型
16.【答案】
【知识点】胡不归模型
17.【答案】(1)解:;
(2)解:,
证明:.
【知识点】探索规律-等式类规律
18.【答案】证明: ,
∴∠B=∠D=∠ACE=90°,
∴∠DCE+∠DEC=∠BCA+∠DCE=90°,
∴∠DEC=∠BCA,
在 和 中,
【知识点】同侧一线三垂直全等模型
19.【答案】(1)解:第4个图案中共有白色地砖23块, 第n个图案中共有白色地砖 块;
(2)解:由题意知,0.8(2n+1)=64.8,
解得n=40,
答:需要灰色地砖40块.
【知识点】探索规律-图形的个数规律
20.【答案】解:根据折叠的性质可知 ,
.
又 是 边的中, ,
点 在以 为圆心, 为半径的圆上运动,
当 三共线时, 的值最, 如图,
,
,
.
【知识点】矩形翻折模型
21世纪教育网(www.21cnjy.com)
2 / 8
2025年九年级数学一轮复习【解题模型】专辑一
一、单选题
1.(2024九下·重庆市模拟)下列图形都是由边长相等且面积为1的等边三角形按一定的规律组成,其中,第①个图形面积为1,第②个图形面积为4,第③个图形面积为9,…,则第⑩个图形中三角形的个数是( )
A.81 B.100 C.99 D.101
2.(2024九上·金堂月考) 如图所示,一场台风过后,垂直于地面的一棵树在距地面1米处折断,树尖B 恰好碰到地面,经测量AB=2,则树高为( )米.
A.1+ B.1+ C.2-1 D.3
3.(2021九上·和平期末)顺次连接对角线互相垂直的四边形的各边中点,所形成的新四边形是( )
A.菱形 B.矩形 C.正方形 D.三角形
4.(2023·容县模拟)我们知道,一元二次方程x2=﹣1没有实数根,即不存在一个实数的平方等于﹣1.若我们规定一个新数“i”,使其满足i2=﹣1(即方程x2=﹣1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=﹣1,i3=i2×i=(﹣1)×i=﹣i,i4=(i2)2=(﹣1)2=1,从而对任意正整数n,我们可以得到i4n+1=i4n×i=(i4)n×i=i,i4n+2=﹣1,i4n+3=﹣i,i4n=1.那么i+i2+i3+…+i2023的值为( )
A.0 B.1 C.﹣1 D.i
5.(2019九上·永登期中)如果顺次连接一个四边形各边中点所得新的四边形是菱形,那么对这个四边形的形状描述最准确的是( )
A.矩形 B.等腰梯形
C.菱形 D.对角线相等的四边形
6.(2024·裕华模拟)如图,一只小蚂蚁在平面直角坐标系中按图中路线进行“爬楼梯”运动,第1次它从原点运动到点,第2次运动到点,第3次运动到点…按这样的规律,经过第2024次运动后,蚂蚁的坐标是( )
A. B. C. D.
7.(2023九上·达州经济开发期末)如图,在Rt△ABC中,∠C=90°,AC=BC,AB=8,点D为AB的中点,若直角MDN绕点D旋转分别交AC于点E,交BC于点F,则下列说法:①AE=CF;②EC+CF=;③DE=DF;④若△ECF的面积为一个定值,则EF的长也是一个定值,其中正确的是( )
A.①② B.①③ C.①②③ D.①②③④
8.(2024九下·上海市期中)顺次联结四边形ABCD各边中点所形成的四边形是矩形,那么四边形ABCD是( )
A.平行四边形 B.矩形 C.菱形 D.等腰梯形
9.(2021·槐荫模拟)如图, ABCD中,AB=2,AD=4,对角线AC、BD相交于点O,点E、F、G、H分别是AO、BO、CO、DO的中点,则下列说法正确的是( )
A.EH=HG
B.△ABO的面积是△EFO的面积的2倍
C.EO=FO
D.四边形EFGH是平行四边形
10.(2024七上·遂宁月考)下图是由同样大小的按一定规律排列而成,其中第①个图形中有4个,第②个图形中有9个,第③个图形中有14个,…,则第⑧个图形中的个数为( )
A.34 B.39 C.40 D.44
二、填空题
11.(2024九上·杭州月考)如图所示,在平南直角坐标系中,半径均为1个单位长度的半目组成一条平此的曲线,点从原点出发、沿这条曲线问右运动,速度为每秒个单位长度,则第2024秒时,点的坐标是 .
12.(2023九下·德清期中)公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如图,若,,则小正方形的面积是 .
13.(2024九下·济南模拟)公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出了“赵爽弦图”.将两个大小相同的“赵爽弦图”(如图1)中的两个小正方形和八个直角三角形按图2方式摆放围成边长为10的正方形,则空白部分面积为
14.(2024·巴东模拟)如图,正方形的边长为1,以为边作第2个正方形,再以为边作第3个正方形,按照这样的规律作下去,第2024个正方形的边长为 .
15.若矩形ABCD的对角线长为10,点E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长是
16.(2024·广元) 如图,在中,,,则的最大值为 .
三、解答题
17.观察下列各式:
第1个等式:;
第2个等式:;
第3个等式:.
(1)请你根据上面三个等式提供的信息,猜想第的变形结果;
(2)按照上面等式反映的规律,写出用(为正整数)表示的等式,并进行验证.
18.如图, 点 在 上, . 求证 : .
19.用灰白两种颜色的正方形地砖, 按如图 所示的规律拼成图案:
(1)第 4 个图案有白色地砖多少块? 第 个图案呢?
(2)已知每个小正方形的边长均为 , 若学校用第 个图案铺设长为 的长廊,则需要灰色地砖多少块?
20.如图,在矩形 中, 是 边的中点, 是线段 边上的动点, 将 沿 所在的直线折叠得到 , 连结 , 求 的最小值.
答案解析部分
1.【答案】B
【知识点】探索规律-图形的递变规律
2.【答案】A
【知识点】风吹树折模型
3.【答案】B
【知识点】中点四边形模型
4.【答案】C
【知识点】探索规律-等式类规律
5.【答案】D
【知识点】中点四边形模型
6.【答案】D
【知识点】探索规律-点的坐标规律
7.【答案】D
【知识点】旋转全等模型
8.【答案】C
【知识点】中点四边形模型
9.【答案】D
【知识点】中点四边形模型
10.【答案】B
【知识点】探索规律-图形的个数规律;探索规律-图形的递变规律
11.【答案】(2024,0)
【知识点】探索规律-点的坐标规律
12.【答案】1
【知识点】“赵爽弦图”模型
13.【答案】50
【知识点】“赵爽弦图”模型
14.【答案】
【知识点】探索规律-图形的递变规律
15.【答案】20
【知识点】中点四边形模型
16.【答案】
【知识点】胡不归模型
17.【答案】(1)解:;
(2)解:,
证明:.
【知识点】探索规律-等式类规律
18.【答案】证明: ,
∴∠B=∠D=∠ACE=90°,
∴∠DCE+∠DEC=∠BCA+∠DCE=90°,
∴∠DEC=∠BCA,
在 和 中,
【知识点】同侧一线三垂直全等模型
19.【答案】(1)解:第4个图案中共有白色地砖23块, 第n个图案中共有白色地砖 块;
(2)解:由题意知,0.8(2n+1)=64.8,
解得n=40,
答:需要灰色地砖40块.
【知识点】探索规律-图形的个数规律
20.【答案】解:根据折叠的性质可知 ,
.
又 是 边的中, ,
点 在以 为圆心, 为半径的圆上运动,
当 三共线时, 的值最, 如图,
,
,
.
【知识点】矩形翻折模型
21世纪教育网(www.21cnjy.com)
2 / 8
同课章节目录
