2025年九年级一轮复习【结合与实践】专题专辑一(含答案)
文档属性
| 名称 | 2025年九年级一轮复习【结合与实践】专题专辑一(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级一轮复习【结合与实践】专题专辑一
一、单选题
1.(2022·榆次模拟)公元前3世纪,古希腊数学家欧几里得编写了《几何原本》.他在编写这本书时挑选一部分数学名词和公认的真命题(即公理)作为证实其他命题的出发点和依据,除公理外,其他命题的真假都需要通过演绎推理的方法进行判断,在此基础上,逐渐形成了一种重要的数学思想,这种思想是( )
A.公理化思想 B.数形结合思想
C.分类讨论思想 D.转化思想
2.(2023九下·石家庄模拟)用正方形纸片剪出一副七巧板,并将其拼成如图的“小天鹅”,设小天鹅的水平宽度为l(左右最大距离),铅垂高度为h(上下最大距离),则的值为( )
A. B. C. D.
3.(2021九下·祁县期中)勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,它也是数学定理中证明方法最多的定理之一.美国第20任总统詹姆斯·加菲尔德的证法如下:
,比较上二式可得.
此证明方法体现的数学思想是( )
A.整体思想 B.转化思想
C.数形结合思想 D.分类讨论思想
4.(2022·侯马期末)数学课上,老师在组织同学们探索多边形的内角和公式时,同学们提出了将此问题转化为已学的三角形内角和知识进行探索的思路.如图是四名同学探索多边形内角和公式时运用的不同的分割方法,将多边形转化为多个三角形,并得出了相同的结论.这四名同学在探索过程中主要体现的数学思想是( )
A.建模思想 B.分类讨论思想
C.数形结合思想 D.转化思想
5.(2021九上·古县期末)在求解一元二次方程﹣2x2+4x+1=0的两个根x1和x2时,某同学使用电脑软件绘制了如图所示的二次函数y=﹣2x2+4x+1的图象,然后通过观察抛物线与x轴的交点,该同学得出﹣1<x1<0,2<x2<3的结论,该同学采用的方法体现的数学思想是( )
A.类比 B.演绎 C.数形结合 D.公理化
6.(2022·寻乌模拟)七巧板是由可以错综分合的几何图案演化而来,它是一种拼板玩具,体现了我国古代劳动人民的智慧,如图1,将一块正方形薄板分为7块,其中包括5块大小不等的三角形,1块正方形和1块平行四边形,图2是由图1拼成的风车形状,则下列等式错误的是( )
A. B. C. D.
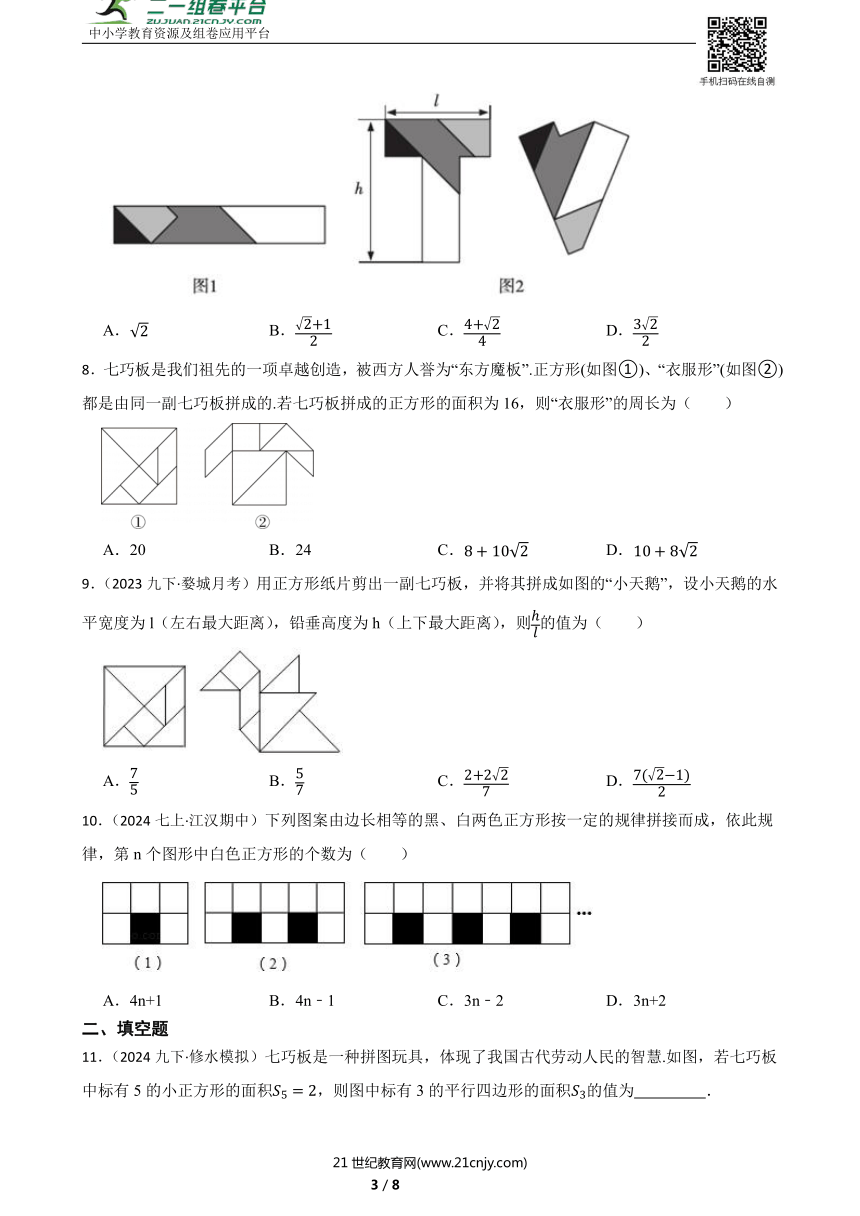
7.(2021·南浔模拟)四巧板是一种类似七巧板的传统智力玩具,它是由一个长方形按如图1分割而成,这几个多边形的内角除了有直角外,还有 角.小明发现可以将四巧板拼搭成如图2的 字形和 字形,那么 字形图中高与宽的比值 为( )
A. B. C. D.
8.七巧板是我们祖先的一项卓越创造,被西方人誉为“东方魔板”.正方形(如图①)、“衣服形”(如图②)都是由同一副七巧板拼成的.若七巧板拼成的正方形的面积为16,则“衣服形”的周长为( )
A.20 B.24 C. D.
9.(2023九下·婺城月考)用正方形纸片剪出一副七巧板,并将其拼成如图的“小天鹅”,设小天鹅的水平宽度为l(左右最大距离),铅垂高度为h(上下最大距离),则的值为( )
A. B. C. D.
10.(2024七上·江汉期中)下列图案由边长相等的黑、白两色正方形按一定的规律拼接而成,依此规律,第n个图形中白色正方形的个数为( )
A.4n+1 B.4n﹣1 C.3n﹣2 D.3n+2
二、填空题
11.(2024九下·修水模拟)七巧板是一种拼图玩具,体现了我国古代劳动人民的智慧.如图,若七巧板中标有5的小正方形的面积,则图中标有3的平行四边形的面积的值为 .
12.(2024·从江模拟)算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大的贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如下表.
数字形式 1 2 3 4 5 6 7 8 9
纵式
横式
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空.示例如下:,则“”表示的数是 .
13.(2023九下·青原模拟)七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,也被誉为“东方魔板”.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”).图①是由边长为8cm的正方形薄板分为7块制作成的“七巧板”,图②是用该“七巧板”拼成的一个“家”的图形.该“七巧板”中7块图形之一的正方形(阴影部分)面积为 .
14.(2023·黄浦模拟)七巧板是中国传统智力玩具,现用以下方法制作一副七巧板:如图所示,取一张边长为20厘米的正方形纸板,联结对角线;分别取中点E、F,连接;过点A作垂线,分别交于G、H两点;分别取中点M、N,联结,沿图中实线剪开即可得到一副七巧板.其中四边形的面积是 平方厘米.
15.(2019·赤峰模拟)P为⊙O内一点,OP=3cm,⊙O的半径为5cm,则经过P点的最短弦长为 cm,最长弦长为 cm.
16.(2024·长沙模拟) 图1是方格绘成的七巧板图案,每个小方格的边长为,现将它剪拼成一个“房子”造型(如图,过左侧的三个端点作圆,并在圆内右侧部分留出矩形作为题字区域(点,,,在圆上,点,在上),形成一幅装饰画,则圆的半径为 .
三、计算题
17.(2024九下·普陀模拟)点游戏是一种扑克牌类的益智类游戏,游戏规则是:从一副扑克牌(去掉大小王)中任意抽取张牌,根据牌面上的数字进行混合运算(每张牌必须用且只能用一次,可以加括号),使得运算结果为或.
例如:抽到的数字为“,,,”,则可列式并计算为:.
如果 、◆表示正, 、 表示负(如“◆”为“”,“ ”为“”),请对下面两组扑克牌按要求进行记数,并按“点”游戏规则对两组数分别进行列式计算,使其运算结果均为或.
①
依次记为:_________________
列式计算:__________________.
②
依次记为:_________________
列式计算:_______.
四、解答题
18.(2024九上·长沙月考)若函数G在m≤x≤n(m<n)上的最大值记为ymax,最小值记为ymin,且满足ymax﹣ymin=1,则称函数G是在m≤x≤n上的“最值差函数”.
(1)函数①;②y=x+1;③y=x2.其中函数 是在1≤x≤2上的“最值差函数”;(填序号)
(2)已知函数G:y=ax2﹣4ax+3a(a>0).
①当a=1时,函数G是在t≤x≤t+1上的“最值差函数”,求t的值;
②函数G是在m+2≤x≤2m+1(m为整数)上的“最值差函数”,且存在整数k,使得,求a的值.
答案解析部分
1.【答案】A
【知识点】数学思想
2.【答案】B
【知识点】七巧板与拼图制作
3.【答案】C
【知识点】数学思想
4.【答案】D
【知识点】数学思想
5.【答案】C
【知识点】数学思想
6.【答案】C
【知识点】七巧板与拼图制作
7.【答案】C
【知识点】七巧板与拼图制作
8.【答案】C
【知识点】七巧板与拼图制作
9.【答案】B
【知识点】七巧板与拼图制作
10.【答案】D
【知识点】猜想与证明
11.【答案】
【知识点】七巧板与拼图制作
12.【答案】7628
【知识点】归纳与类比
13.【答案】
【知识点】七巧板与拼图制作
14.【答案】50
【知识点】七巧板与拼图制作
15.【答案】8;10
【知识点】数学思想
16.【答案】5
【知识点】七巧板与拼图制作
17.【答案】①,,,;.(答案不唯一,正确即可)
②,,,;.(答案不唯一,正确即可)
【知识点】“二十四点”游戏
18.【答案】(1)②
(2)解:①当a=1时,二次函数G:y=ax2﹣4ax+3a(a>0)为y=x2﹣4x+3,对称轴为直线x=2.
当x=t时,,
当x=t+1时,
当x=2时,y3=﹣1.
若t>2,则y2﹣y1=1,解得t=2(舍去);
若,则y2﹣y3=1,解得t=0(舍去),t=2;
若,则y1﹣y3=1,解得t=1,t=3(舍去);
若t<1,则y1﹣y2=1,解得t=1(舍去).
综上所述,t=1或t=2;
②∵二次函数y=ax2﹣4ax+3a(a>0)的对称轴为直线x=2,
又∵m+2≤x≤2m+1,
∴m>1,
∴2<m+2≤x≤2m+1,
∴当2<m+2≤x≤2m+1时,y随x的增大而增大,
∴当x=2m+1时取得最大值,x=m+2时取得最小值,
∴,
∴m,k为整数,且m>1,
∴m的值为3,
又∵ymax﹣ymin=1,
∴a(6+1)2﹣4a(6+1)+3a﹣[a(3+2)2﹣4a(3+2)+3a]=1,
∴.
【知识点】数学思想;二次函数的其他应用
21世纪教育网(www.21cnjy.com)
1 / 8
2025年九年级一轮复习【结合与实践】专题专辑一
一、单选题
1.(2022·榆次模拟)公元前3世纪,古希腊数学家欧几里得编写了《几何原本》.他在编写这本书时挑选一部分数学名词和公认的真命题(即公理)作为证实其他命题的出发点和依据,除公理外,其他命题的真假都需要通过演绎推理的方法进行判断,在此基础上,逐渐形成了一种重要的数学思想,这种思想是( )
A.公理化思想 B.数形结合思想
C.分类讨论思想 D.转化思想
2.(2023九下·石家庄模拟)用正方形纸片剪出一副七巧板,并将其拼成如图的“小天鹅”,设小天鹅的水平宽度为l(左右最大距离),铅垂高度为h(上下最大距离),则的值为( )
A. B. C. D.
3.(2021九下·祁县期中)勾股定理是人类早期发现并证明的重要数学定理之一,是用代数思想解决几何问题的最重要的工具之一,它也是数学定理中证明方法最多的定理之一.美国第20任总统詹姆斯·加菲尔德的证法如下:
,比较上二式可得.
此证明方法体现的数学思想是( )
A.整体思想 B.转化思想
C.数形结合思想 D.分类讨论思想
4.(2022·侯马期末)数学课上,老师在组织同学们探索多边形的内角和公式时,同学们提出了将此问题转化为已学的三角形内角和知识进行探索的思路.如图是四名同学探索多边形内角和公式时运用的不同的分割方法,将多边形转化为多个三角形,并得出了相同的结论.这四名同学在探索过程中主要体现的数学思想是( )
A.建模思想 B.分类讨论思想
C.数形结合思想 D.转化思想
5.(2021九上·古县期末)在求解一元二次方程﹣2x2+4x+1=0的两个根x1和x2时,某同学使用电脑软件绘制了如图所示的二次函数y=﹣2x2+4x+1的图象,然后通过观察抛物线与x轴的交点,该同学得出﹣1<x1<0,2<x2<3的结论,该同学采用的方法体现的数学思想是( )
A.类比 B.演绎 C.数形结合 D.公理化
6.(2022·寻乌模拟)七巧板是由可以错综分合的几何图案演化而来,它是一种拼板玩具,体现了我国古代劳动人民的智慧,如图1,将一块正方形薄板分为7块,其中包括5块大小不等的三角形,1块正方形和1块平行四边形,图2是由图1拼成的风车形状,则下列等式错误的是( )
A. B. C. D.
7.(2021·南浔模拟)四巧板是一种类似七巧板的传统智力玩具,它是由一个长方形按如图1分割而成,这几个多边形的内角除了有直角外,还有 角.小明发现可以将四巧板拼搭成如图2的 字形和 字形,那么 字形图中高与宽的比值 为( )
A. B. C. D.
8.七巧板是我们祖先的一项卓越创造,被西方人誉为“东方魔板”.正方形(如图①)、“衣服形”(如图②)都是由同一副七巧板拼成的.若七巧板拼成的正方形的面积为16,则“衣服形”的周长为( )
A.20 B.24 C. D.
9.(2023九下·婺城月考)用正方形纸片剪出一副七巧板,并将其拼成如图的“小天鹅”,设小天鹅的水平宽度为l(左右最大距离),铅垂高度为h(上下最大距离),则的值为( )
A. B. C. D.
10.(2024七上·江汉期中)下列图案由边长相等的黑、白两色正方形按一定的规律拼接而成,依此规律,第n个图形中白色正方形的个数为( )
A.4n+1 B.4n﹣1 C.3n﹣2 D.3n+2
二、填空题
11.(2024九下·修水模拟)七巧板是一种拼图玩具,体现了我国古代劳动人民的智慧.如图,若七巧板中标有5的小正方形的面积,则图中标有3的平行四边形的面积的值为 .
12.(2024·从江模拟)算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做出了很大的贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字,如下表.
数字形式 1 2 3 4 5 6 7 8 9
纵式
横式
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空.示例如下:,则“”表示的数是 .
13.(2023九下·青原模拟)七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经历代演变而成七巧板,也被誉为“东方魔板”.19世纪传到国外,被称为“唐图”(意为“来自中国的拼图”).图①是由边长为8cm的正方形薄板分为7块制作成的“七巧板”,图②是用该“七巧板”拼成的一个“家”的图形.该“七巧板”中7块图形之一的正方形(阴影部分)面积为 .
14.(2023·黄浦模拟)七巧板是中国传统智力玩具,现用以下方法制作一副七巧板:如图所示,取一张边长为20厘米的正方形纸板,联结对角线;分别取中点E、F,连接;过点A作垂线,分别交于G、H两点;分别取中点M、N,联结,沿图中实线剪开即可得到一副七巧板.其中四边形的面积是 平方厘米.
15.(2019·赤峰模拟)P为⊙O内一点,OP=3cm,⊙O的半径为5cm,则经过P点的最短弦长为 cm,最长弦长为 cm.
16.(2024·长沙模拟) 图1是方格绘成的七巧板图案,每个小方格的边长为,现将它剪拼成一个“房子”造型(如图,过左侧的三个端点作圆,并在圆内右侧部分留出矩形作为题字区域(点,,,在圆上,点,在上),形成一幅装饰画,则圆的半径为 .
三、计算题
17.(2024九下·普陀模拟)点游戏是一种扑克牌类的益智类游戏,游戏规则是:从一副扑克牌(去掉大小王)中任意抽取张牌,根据牌面上的数字进行混合运算(每张牌必须用且只能用一次,可以加括号),使得运算结果为或.
例如:抽到的数字为“,,,”,则可列式并计算为:.
如果 、◆表示正, 、 表示负(如“◆”为“”,“ ”为“”),请对下面两组扑克牌按要求进行记数,并按“点”游戏规则对两组数分别进行列式计算,使其运算结果均为或.
①
依次记为:_________________
列式计算:__________________.
②
依次记为:_________________
列式计算:_______.
四、解答题
18.(2024九上·长沙月考)若函数G在m≤x≤n(m<n)上的最大值记为ymax,最小值记为ymin,且满足ymax﹣ymin=1,则称函数G是在m≤x≤n上的“最值差函数”.
(1)函数①;②y=x+1;③y=x2.其中函数 是在1≤x≤2上的“最值差函数”;(填序号)
(2)已知函数G:y=ax2﹣4ax+3a(a>0).
①当a=1时,函数G是在t≤x≤t+1上的“最值差函数”,求t的值;
②函数G是在m+2≤x≤2m+1(m为整数)上的“最值差函数”,且存在整数k,使得,求a的值.
答案解析部分
1.【答案】A
【知识点】数学思想
2.【答案】B
【知识点】七巧板与拼图制作
3.【答案】C
【知识点】数学思想
4.【答案】D
【知识点】数学思想
5.【答案】C
【知识点】数学思想
6.【答案】C
【知识点】七巧板与拼图制作
7.【答案】C
【知识点】七巧板与拼图制作
8.【答案】C
【知识点】七巧板与拼图制作
9.【答案】B
【知识点】七巧板与拼图制作
10.【答案】D
【知识点】猜想与证明
11.【答案】
【知识点】七巧板与拼图制作
12.【答案】7628
【知识点】归纳与类比
13.【答案】
【知识点】七巧板与拼图制作
14.【答案】50
【知识点】七巧板与拼图制作
15.【答案】8;10
【知识点】数学思想
16.【答案】5
【知识点】七巧板与拼图制作
17.【答案】①,,,;.(答案不唯一,正确即可)
②,,,;.(答案不唯一,正确即可)
【知识点】“二十四点”游戏
18.【答案】(1)②
(2)解:①当a=1时,二次函数G:y=ax2﹣4ax+3a(a>0)为y=x2﹣4x+3,对称轴为直线x=2.
当x=t时,,
当x=t+1时,
当x=2时,y3=﹣1.
若t>2,则y2﹣y1=1,解得t=2(舍去);
若,则y2﹣y3=1,解得t=0(舍去),t=2;
若,则y1﹣y3=1,解得t=1,t=3(舍去);
若t<1,则y1﹣y2=1,解得t=1(舍去).
综上所述,t=1或t=2;
②∵二次函数y=ax2﹣4ax+3a(a>0)的对称轴为直线x=2,
又∵m+2≤x≤2m+1,
∴m>1,
∴2<m+2≤x≤2m+1,
∴当2<m+2≤x≤2m+1时,y随x的增大而增大,
∴当x=2m+1时取得最大值,x=m+2时取得最小值,
∴,
∴m,k为整数,且m>1,
∴m的值为3,
又∵ymax﹣ymin=1,
∴a(6+1)2﹣4a(6+1)+3a﹣[a(3+2)2﹣4a(3+2)+3a]=1,
∴.
【知识点】数学思想;二次函数的其他应用
21世纪教育网(www.21cnjy.com)
1 / 8
同课章节目录
