第七单元 折线统计图 --2024-2025学年人教版五年级数学下册单元测试卷(含答案)
文档属性
| 名称 | 第七单元 折线统计图 --2024-2025学年人教版五年级数学下册单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1000.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 18:20:22 | ||
图片预览


文档简介
第七单元 折线统计图
一、单选题
1.要统计下面的各项信息,其中适合用折线统计图表示的是( )
①动物园各种动物的只数 ②某地一年的降水量变化情况
③小兰1至10岁体重变化的情况 ④雯雯这次期末考试各科的成绩
A.①②③④ B.②③④ C.②③ D.①④
2.下面的情况中,最适合用复式折线统计图表示的是( )
A.瑞安市今年5月份日平均气温变化情况
B.某校五年级各班男生、女生具体人数
C.两家零售店去年12个月销售额变化情况
D.小丽最近4次数学测试成绩变化情况
3.王老师在一楼的食堂打了早餐,回到四楼的办公室开始吃早餐。第一、二节课到二楼的教室上课,第三、四节课在办公室批改作业,下课后,下楼回家休息。下面( )正确描述了王老师上午的活动。
A. B. C. D.
4.下面的信息不适合用折线统计图表示的是( ).
A.2021年漳平市月降水量变化情况
B.黄强上学期期末测试各科的成绩
C.小辉1到10岁体重的变化情况
D.风景区2021年1-12月份旅游人数的变化情况
5.下图的折线统计图不可能是关于 ( )的统计图。
A.哥哥本期数学成绩
B.小红的身高变化
C.服装厂去年每个月的产量
6.记录2023年大勇一家每月的收入和支出的变化情况,选用( )统计图。
A.单式折线 B.单式条形 C.复式条形 D.复式折线
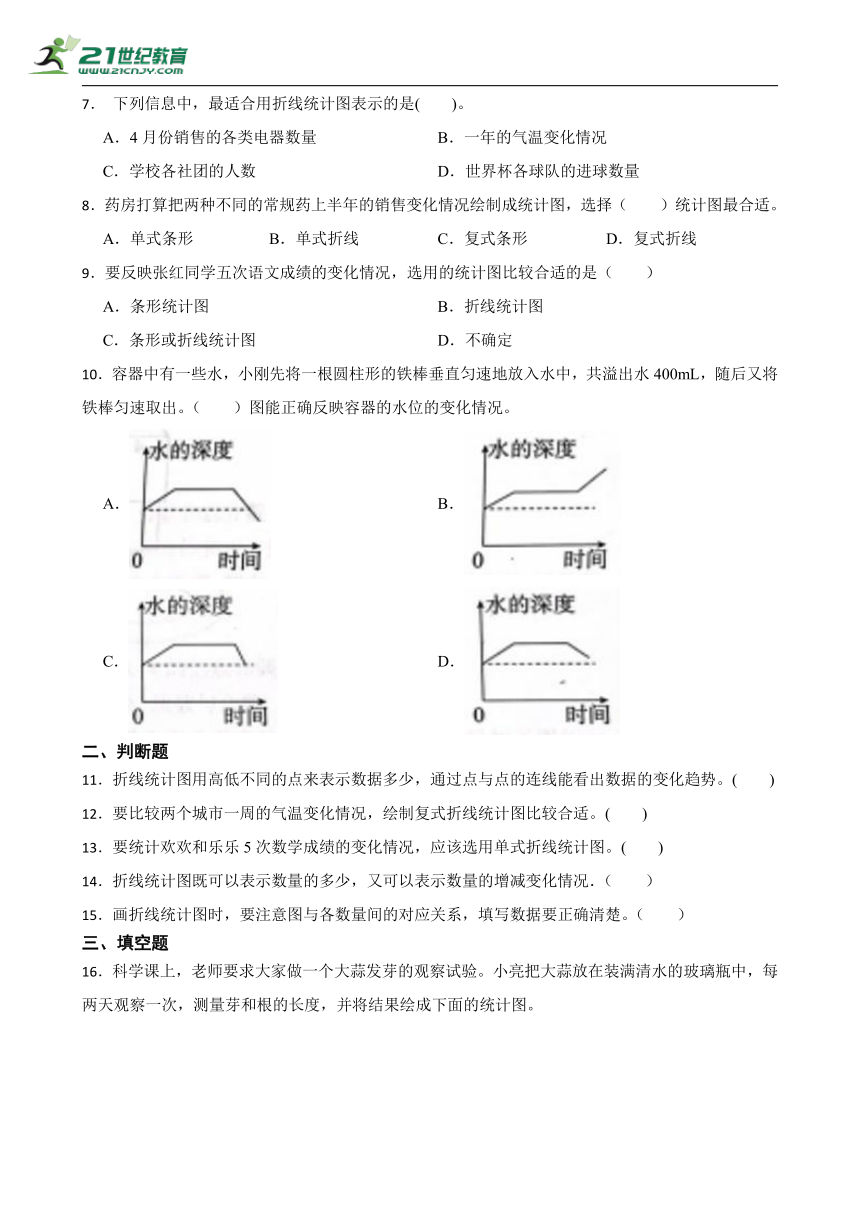
7. 下列信息中,最适合用折线统计图表示的是( )。
A.4月份销售的各类电器数量 B.一年的气温变化情况
C.学校各社团的人数 D.世界杯各球队的进球数量
8.药房打算把两种不同的常规药上半年的销售变化情况绘制成统计图,选择( )统计图最合适。
A.单式条形 B.单式折线 C.复式条形 D.复式折线
9.要反映张红同学五次语文成绩的变化情况,选用的统计图比较合适的是( )
A.条形统计图 B.折线统计图
C.条形或折线统计图 D.不确定
10.容器中有一些水,小刚先将一根圆柱形的铁棒垂直匀速地放入水中,共溢出水400mL,随后又将铁棒匀速取出。( )图能正确反映容器的水位的变化情况。
A. B.
C. D.
二、判断题
11.折线统计图用高低不同的点来表示数据多少,通过点与点的连线能看出数据的变化趋势。( )
12.要比较两个城市一周的气温变化情况,绘制复式折线统计图比较合适。( )
13.要统计欢欢和乐乐5次数学成绩的变化情况,应该选用单式折线统计图。( )
14.折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况.( )
15.画折线统计图时,要注意图与各数量间的对应关系,填写数据要正确清楚。( )
三、填空题
16.科学课上,老师要求大家做一个大蒜发芽的观察试验。小亮把大蒜放在装满清水的玻璃瓶中,每两天观察一次,测量芽和根的长度,并将结果绘成下面的统计图。
(1)大蒜的根和芽在这个阶段生长总体呈 趋势。
(2)小亮发现大蒜是第 天开始生根,再过 天开始发芽。
(3)第10天时,芽的长度是根的 。
17.近年来,各地积极开展惠民直播,充分发挥自身优势,为当地经济创收增色。
下图记录了4月份河北省某地苹果和梨的几场直播的销售情况。
(1)在 日苹果的销量最低,在 日梨的销量最高。
(2)在 日两种水果的销量相差最大,相差了 箱。
(3)在这个月的几场直播中,苹果一共卖出 ,比梨少 箱。
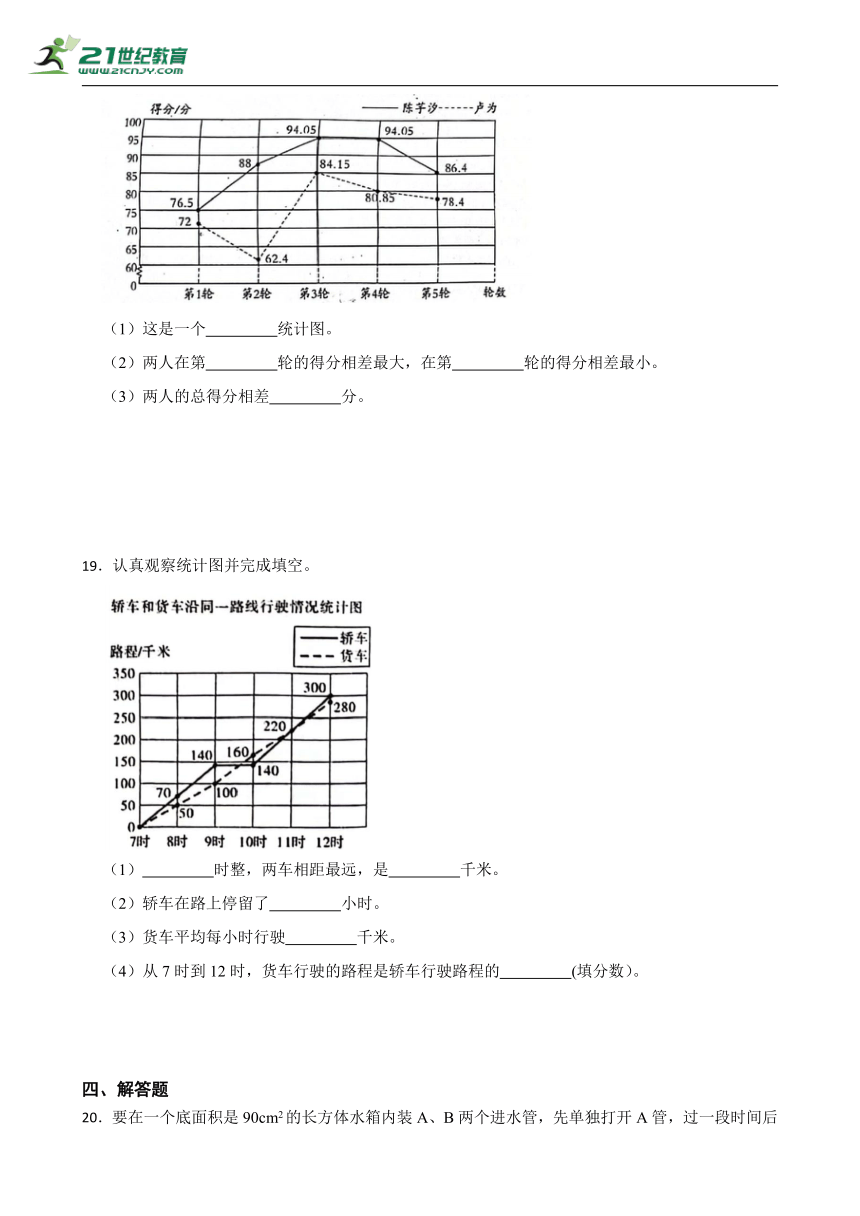
18.在第18届国际泳联世锦赛女子单人10米台比赛中,两位中国选手陈芋汐、卢为分获冠、亚军。以下是两位选手5轮比赛的得分情况统计图。
(1)这是一个 统计图。
(2)两人在第 轮的得分相差最大,在第 轮的得分相差最小。
(3)两人的总得分相差 分。
19.认真观察统计图并完成填空。
(1) 时整,两车相距最远,是 千米。
(2)轿车在路上停留了 小时。
(3)货车平均每小时行驶 千米。
(4)从7时到12时,货车行驶的路程是轿车行驶路程的 (填分数)。
四、解答题
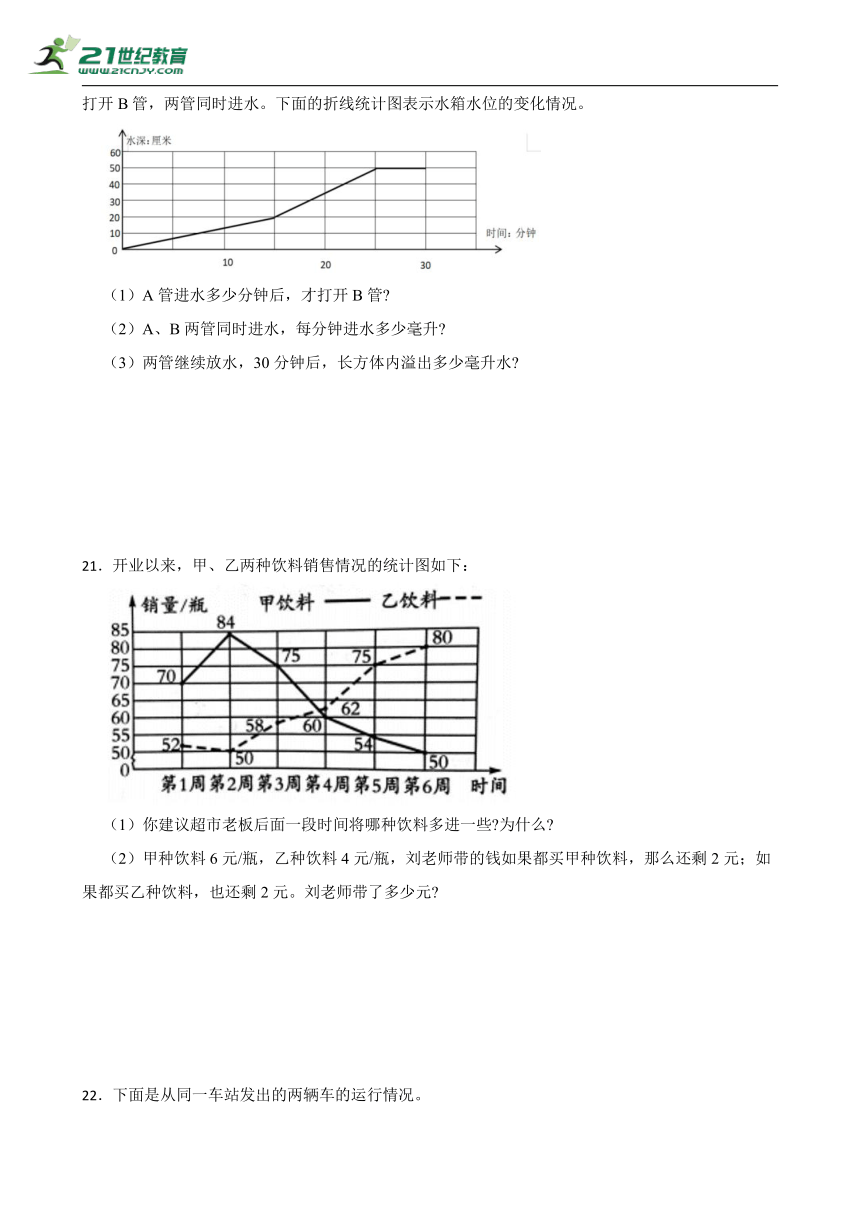
20.要在一个底面积是90cm2的长方体水箱内装A、B两个进水管,先单独打开A管,过一段时间后打开B管,两管同时进水。下面的折线统计图表示水箱水位的变化情况。
(1)A管进水多少分钟后,才打开B管
(2)A、B两管同时进水,每分钟进水多少毫升
(3)两管继续放水,30分钟后,长方体内溢出多少毫升水
21.开业以来,甲、乙两种饮料销售情况的统计图如下:
(1)你建议超市老板后面一段时间将哪种饮料多进一些 为什么
(2)甲种饮料6元/瓶,乙种饮料4元/瓶,刘老师带的钱如果都买甲种饮料,那么还剩2元;如果都买乙种饮料,也还剩2元。刘老师带了多少元
22.下面是从同一车站发出的两辆车的运行情况。
(1)2路车与4路车在 第二次相遇。
(2)2路车和4路车平均每小时各行多少千米
(3)在4路车开出几小时后,两车行驶的路程相差最多 相差多少千米
23.下图是水管往水箱里注水情况统计图。在水箱里装有A、B两个进水管,先开A管,过一段时间后,两管同时开,请看下图回答问题。
(1)打开B管前,A管打开了多长时间?水位是多少厘米?
(2)A、B两管同时打开了多长时间?水位上升了多少厘米?
(3)A、B两管同时打开,平均每分钟水位上升多少厘米?
答案解析部分
1.C
解:①动物园各种动物的只数,适合用条形统计图,
②某地一年的降水量变化情况,适合用折线统计图,
③小兰1至10岁体重变化的情况,适合用折线统计图,
④雯雯这次期末考试各科的成绩,适合用条形统计图。
故答案为:C。
条形统计图可以清楚的表示出数据的多少;折线统计图不但可以表示出数据的多少,还可以描述出其变化趋势。
2.C
解:A项:适合用单式折线统计图表示;
B项:适合用复式条形统计图表示;
C项:适合用复式折线统计图表示;
D项:适合用单式折线统计图表示。
故答案为:C。
适合用复式条形统计图表示首先得是两项内容,并且清楚地看出数量的增减变化情况。
3.C
解:第三个图正确描述了王老师上午的活动。
故答案为:C。
根据楼层的不同和时间的不同进行区分。
4.B
解:黄强上学期期末测试各科的成绩,适合用条形统计图,不适合用折线统计图。
故答案为:B。
条形统计图可以清楚的表示出数据的多少;折线统计图不但可以表示出数据的多少,还可以描述出其变化趋势。
5.B
解:下图的折线统计图不可能是关于小红的身高变化的统计图。
故答案为:B。
小红的身高变化不应该中间会变矮。
6.D
解:因为是收入和支出这两项,并且还是变化情况,则选用复式折线统计图。
故答案为:D。
如果要统计的数据是两项或者以上,要选用复式统计图,并且折线统计图不仅能清楚地反映出数量的多少,还能清楚地看出数量的增减变化情况。
7.B
解:A:要表示的是各类电器的具体销售数量 ,适合用条形统计图;
B:一年的气温变化情况适合用折线统计图表示;
C:学校各社团的具体人数适合用条形统计图表示;
D:世界杯各球队的进球数量,适合用条形统计图表示。
故答案为:B。
要表示具体的数值,用条形统计图;要表示变化情况,用折线统计图。
8.D
解:选择复式折线统计图最合适。
故答案为:D。
“两种”决定用复式,“变化”决定用折线,据此解答。
9.B
解:要反映多次的成绩变化情况,选用折线统计图比较合适。
故答案为:B。
折线统计图是以折线的上升或下降来表示统计数量的增减变化的统计图,它可以反映数据的增减变化情况。
10.A
解:铁棒垂直匀速地放入水中时,随着时间的增加,水的深度也在增加,
增加到容器口后,随着时间的增加,水的深度不变;
将铁棒匀速取出时,随着时间的增加,水的深度在减少,最后水的深度要低于原来水的深度,
第一个图形能正确反映容器的水位的变化情况。
故答案为:A。
先想象实际操作的情况,再根据实际情况逐段分析,据此解答。
11.正确
解:题目描述中提到,“折线统计图用高低不同的点来表示数据多少,通过点与点的连线能看出数据的变化趋势”。这正是折线统计图的基本特征,因此,题目描述是正确的。
故答案为:正确。
此题考查折线统计图的特点。折线统计图不仅能够清晰地显示数据的多少,而且能够通过观察折线的变化,直观地反映数据的变化趋势。
12.正确
解:要比较两个城市一周的气温变化情况,绘制复式折线统计图比较合适。原题说法正确。
故答案为:正确。
“两个城市”,据此可以看出用复式;“变化情况”,据此可以看出用折线;综合起来就是用复式折线统计图比较合适。
13.错误
解:折线统计图能清楚地看出数量的增减变化情况,因为是两人,所以要统计欢欢和乐乐5次数学成绩的变化情况,应该选用复式折线统计图,原题干说法错误。
故答案为:错误。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
14.正确
折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况。故答案为:正确
根据折线统计图的特点,折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况。
15.正确
解:画折线统计图时,要注意图与各数量间的对应关系,填写数据要正确清楚。
故答案为:正确。
根据折线统计图的特征作答即可。
16.(1)上升
(2)4;4
(3)
解:(1)蒜的根和芽在这个阶段生长总体呈上升趋势;
(2)小亮发现大蒜是第4天开始生根,再过4天开始发芽;
(3)10÷40=。
故答案为:(1)上升;(2)4;4;(3)。
(1)、(2)观察统计图可知:蒜的根和芽在这个阶段生长总体呈上升趋势;小亮发现大蒜是第4天开始生根,再过4天开始发芽;
(3)第10天时,芽的长度是根的分率=第10天芽的长度÷根的长度。
17.(1)7;30
(2)18;12
(3)200;35
解:(1)在7日苹果的销量最低,在30日梨的销量最高。
(2)40-28=12(箱)
在18日两种水果的销量相差最大,相差了12箱。
(3)苹果:35+27+30+28+35+45=200(箱)
梨:28+35+32+40+45+55=235(箱)
235-200=35(箱)
苹果一共卖出200,比梨少35箱。
故答案为:(1)7;30;(2)18;12;(3)200;35。
(1)苹果的销量中27最小,梨的销量中55最大,据此解答;
(2)两种水果的销量之间的格数最多,说明销量相差最大,他们的差就是相差的箱数;
(3)先分别算出苹果一共卖出的箱数,梨一共卖出的箱数,再计算它们的差。
18.(1)折线
(2)2;1
(3)61.2
解:(1)这是一个折线统计图;
(2)两人在第2轮的得分相差最大,在第1轮的得分相差最小;
(3)(76.5+88+94.05+94.05+86.4)-(72+62.4+84.15+80.85+78.4)
=439-377.8
=61.2(分)
故答案为:(1)折线;(2)2;1;(3)61.2。
(1)用折线来表示数据的大小和增减变化情况,这是折线统计图;
(2)根据每个轮次两人的得分结合图形可以判断哪轮得分相差最大,哪轮得分相差最小;
(3)把两人的总得分相减即可求出相差的分数。
19.(1)9;40
(2)1
(3)56
(4)
解:(1)9时整,列车相距最远,是140-100=40(千米);
(2)10时-9时=1小时;
(3)280÷5=56(千米);
(4)280÷300=。
故答案为:(1)9;40;(2)1;(3)56;(4)。
(1)实线表示轿车,虚线表示货车,9时轿车行驶140千米,货车行驶100千米,此时两车的距离最远;
(2)从9时到10时之间是轿车在路上停留的时间;
(3)用货车行驶的路程除以时间即可求出货车平均每小时行驶的路程;
(4)货车行了280千米,轿车行了300千米,用货车行的路程除以轿车行的路程即可求出货车行驶的路程是轿车行驶路程的几分之几。
20.(1)解: 从图上可以看出,A管进水15分钟后,才打开B管。
(2)解:25-15=10(分)
50-20=30(厘米)
30÷10=3(厘米)
80×3=240(立方厘米)=240(毫升)
答:每分钟进水240毫升。
(3)解:30-25=5(分)
5×3=15(cm)
15×80=1200(mL)
答:长方体内溢出1200毫升的水。
(1)0~15分的折线时匀速向上走,15分钟的时候折线开始向上走,据此解答;
(2)A、B两管同时进水时间是10分钟,水深增加了30厘米,说明1分钟水深增加3厘米,水箱的底面积×1分钟增加的水深=每分钟进水的体积。
21.(1)答:我建议超市老板后面一段时间将乙饮料多进一些。因为乙饮料的销量呈上升趋势,甲饮料的销量呈下降趋势。
(2)解:6=2×3,4=2×2
6和4的最小公倍数是2×2×3=12
12+2=14(元)
答:刘老师带了14元。
(1)甲饮料的销量在下降,乙饮料的销量在上升,所以建议超市老板后面一段时间将乙饮料多进一些;
(2)刘老师带的钱数=6和4的最小公倍数+2元,据此解答。
22.(1)10:00
(2)解:2路车:100÷4=25(千米/时)
4路车:(千米/时)
答:2路车平均每小时行25千米;4路车平均每小时行33千米。
(3)解:9时-7时=2个小时
80-40=40(千米)
答:在4路车开出2小时,两车行驶的路程相差最多,相差40千米。
解:(1)2路车与4路车在7点半左右第一次相遇,10点钟第二次相遇。
故答案为:(1)10:00。
(1)两条线相交于一点,就说明两车相遇了;
(2)行驶的路程÷行驶的时间=行驶的速度;
(3)两条线之间的格数越多,说明相差最多,大数-小数=相差的千米数。
23.(1)15 分钟 20 厘米
(2)解:25- 15=10(分钟) 60-20= 40(厘米)
(3)解:40÷10=4(厘米)
一、单选题
1.要统计下面的各项信息,其中适合用折线统计图表示的是( )
①动物园各种动物的只数 ②某地一年的降水量变化情况
③小兰1至10岁体重变化的情况 ④雯雯这次期末考试各科的成绩
A.①②③④ B.②③④ C.②③ D.①④
2.下面的情况中,最适合用复式折线统计图表示的是( )
A.瑞安市今年5月份日平均气温变化情况
B.某校五年级各班男生、女生具体人数
C.两家零售店去年12个月销售额变化情况
D.小丽最近4次数学测试成绩变化情况
3.王老师在一楼的食堂打了早餐,回到四楼的办公室开始吃早餐。第一、二节课到二楼的教室上课,第三、四节课在办公室批改作业,下课后,下楼回家休息。下面( )正确描述了王老师上午的活动。
A. B. C. D.
4.下面的信息不适合用折线统计图表示的是( ).
A.2021年漳平市月降水量变化情况
B.黄强上学期期末测试各科的成绩
C.小辉1到10岁体重的变化情况
D.风景区2021年1-12月份旅游人数的变化情况
5.下图的折线统计图不可能是关于 ( )的统计图。
A.哥哥本期数学成绩
B.小红的身高变化
C.服装厂去年每个月的产量
6.记录2023年大勇一家每月的收入和支出的变化情况,选用( )统计图。
A.单式折线 B.单式条形 C.复式条形 D.复式折线
7. 下列信息中,最适合用折线统计图表示的是( )。
A.4月份销售的各类电器数量 B.一年的气温变化情况
C.学校各社团的人数 D.世界杯各球队的进球数量
8.药房打算把两种不同的常规药上半年的销售变化情况绘制成统计图,选择( )统计图最合适。
A.单式条形 B.单式折线 C.复式条形 D.复式折线
9.要反映张红同学五次语文成绩的变化情况,选用的统计图比较合适的是( )
A.条形统计图 B.折线统计图
C.条形或折线统计图 D.不确定
10.容器中有一些水,小刚先将一根圆柱形的铁棒垂直匀速地放入水中,共溢出水400mL,随后又将铁棒匀速取出。( )图能正确反映容器的水位的变化情况。
A. B.
C. D.
二、判断题
11.折线统计图用高低不同的点来表示数据多少,通过点与点的连线能看出数据的变化趋势。( )
12.要比较两个城市一周的气温变化情况,绘制复式折线统计图比较合适。( )
13.要统计欢欢和乐乐5次数学成绩的变化情况,应该选用单式折线统计图。( )
14.折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况.( )
15.画折线统计图时,要注意图与各数量间的对应关系,填写数据要正确清楚。( )
三、填空题
16.科学课上,老师要求大家做一个大蒜发芽的观察试验。小亮把大蒜放在装满清水的玻璃瓶中,每两天观察一次,测量芽和根的长度,并将结果绘成下面的统计图。
(1)大蒜的根和芽在这个阶段生长总体呈 趋势。
(2)小亮发现大蒜是第 天开始生根,再过 天开始发芽。
(3)第10天时,芽的长度是根的 。
17.近年来,各地积极开展惠民直播,充分发挥自身优势,为当地经济创收增色。
下图记录了4月份河北省某地苹果和梨的几场直播的销售情况。
(1)在 日苹果的销量最低,在 日梨的销量最高。
(2)在 日两种水果的销量相差最大,相差了 箱。
(3)在这个月的几场直播中,苹果一共卖出 ,比梨少 箱。
18.在第18届国际泳联世锦赛女子单人10米台比赛中,两位中国选手陈芋汐、卢为分获冠、亚军。以下是两位选手5轮比赛的得分情况统计图。
(1)这是一个 统计图。
(2)两人在第 轮的得分相差最大,在第 轮的得分相差最小。
(3)两人的总得分相差 分。
19.认真观察统计图并完成填空。
(1) 时整,两车相距最远,是 千米。
(2)轿车在路上停留了 小时。
(3)货车平均每小时行驶 千米。
(4)从7时到12时,货车行驶的路程是轿车行驶路程的 (填分数)。
四、解答题
20.要在一个底面积是90cm2的长方体水箱内装A、B两个进水管,先单独打开A管,过一段时间后打开B管,两管同时进水。下面的折线统计图表示水箱水位的变化情况。
(1)A管进水多少分钟后,才打开B管
(2)A、B两管同时进水,每分钟进水多少毫升
(3)两管继续放水,30分钟后,长方体内溢出多少毫升水
21.开业以来,甲、乙两种饮料销售情况的统计图如下:
(1)你建议超市老板后面一段时间将哪种饮料多进一些 为什么
(2)甲种饮料6元/瓶,乙种饮料4元/瓶,刘老师带的钱如果都买甲种饮料,那么还剩2元;如果都买乙种饮料,也还剩2元。刘老师带了多少元
22.下面是从同一车站发出的两辆车的运行情况。
(1)2路车与4路车在 第二次相遇。
(2)2路车和4路车平均每小时各行多少千米
(3)在4路车开出几小时后,两车行驶的路程相差最多 相差多少千米
23.下图是水管往水箱里注水情况统计图。在水箱里装有A、B两个进水管,先开A管,过一段时间后,两管同时开,请看下图回答问题。
(1)打开B管前,A管打开了多长时间?水位是多少厘米?
(2)A、B两管同时打开了多长时间?水位上升了多少厘米?
(3)A、B两管同时打开,平均每分钟水位上升多少厘米?
答案解析部分
1.C
解:①动物园各种动物的只数,适合用条形统计图,
②某地一年的降水量变化情况,适合用折线统计图,
③小兰1至10岁体重变化的情况,适合用折线统计图,
④雯雯这次期末考试各科的成绩,适合用条形统计图。
故答案为:C。
条形统计图可以清楚的表示出数据的多少;折线统计图不但可以表示出数据的多少,还可以描述出其变化趋势。
2.C
解:A项:适合用单式折线统计图表示;
B项:适合用复式条形统计图表示;
C项:适合用复式折线统计图表示;
D项:适合用单式折线统计图表示。
故答案为:C。
适合用复式条形统计图表示首先得是两项内容,并且清楚地看出数量的增减变化情况。
3.C
解:第三个图正确描述了王老师上午的活动。
故答案为:C。
根据楼层的不同和时间的不同进行区分。
4.B
解:黄强上学期期末测试各科的成绩,适合用条形统计图,不适合用折线统计图。
故答案为:B。
条形统计图可以清楚的表示出数据的多少;折线统计图不但可以表示出数据的多少,还可以描述出其变化趋势。
5.B
解:下图的折线统计图不可能是关于小红的身高变化的统计图。
故答案为:B。
小红的身高变化不应该中间会变矮。
6.D
解:因为是收入和支出这两项,并且还是变化情况,则选用复式折线统计图。
故答案为:D。
如果要统计的数据是两项或者以上,要选用复式统计图,并且折线统计图不仅能清楚地反映出数量的多少,还能清楚地看出数量的增减变化情况。
7.B
解:A:要表示的是各类电器的具体销售数量 ,适合用条形统计图;
B:一年的气温变化情况适合用折线统计图表示;
C:学校各社团的具体人数适合用条形统计图表示;
D:世界杯各球队的进球数量,适合用条形统计图表示。
故答案为:B。
要表示具体的数值,用条形统计图;要表示变化情况,用折线统计图。
8.D
解:选择复式折线统计图最合适。
故答案为:D。
“两种”决定用复式,“变化”决定用折线,据此解答。
9.B
解:要反映多次的成绩变化情况,选用折线统计图比较合适。
故答案为:B。
折线统计图是以折线的上升或下降来表示统计数量的增减变化的统计图,它可以反映数据的增减变化情况。
10.A
解:铁棒垂直匀速地放入水中时,随着时间的增加,水的深度也在增加,
增加到容器口后,随着时间的增加,水的深度不变;
将铁棒匀速取出时,随着时间的增加,水的深度在减少,最后水的深度要低于原来水的深度,
第一个图形能正确反映容器的水位的变化情况。
故答案为:A。
先想象实际操作的情况,再根据实际情况逐段分析,据此解答。
11.正确
解:题目描述中提到,“折线统计图用高低不同的点来表示数据多少,通过点与点的连线能看出数据的变化趋势”。这正是折线统计图的基本特征,因此,题目描述是正确的。
故答案为:正确。
此题考查折线统计图的特点。折线统计图不仅能够清晰地显示数据的多少,而且能够通过观察折线的变化,直观地反映数据的变化趋势。
12.正确
解:要比较两个城市一周的气温变化情况,绘制复式折线统计图比较合适。原题说法正确。
故答案为:正确。
“两个城市”,据此可以看出用复式;“变化情况”,据此可以看出用折线;综合起来就是用复式折线统计图比较合适。
13.错误
解:折线统计图能清楚地看出数量的增减变化情况,因为是两人,所以要统计欢欢和乐乐5次数学成绩的变化情况,应该选用复式折线统计图,原题干说法错误。
故答案为:错误。
条形统计图能清楚地看出数量的多少;折线统计图能清楚地看出数量的增减变化情况。
14.正确
折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况。故答案为:正确
根据折线统计图的特点,折线统计图既可以表示数量的多少,又可以表示数量的增减变化情况。
15.正确
解:画折线统计图时,要注意图与各数量间的对应关系,填写数据要正确清楚。
故答案为:正确。
根据折线统计图的特征作答即可。
16.(1)上升
(2)4;4
(3)
解:(1)蒜的根和芽在这个阶段生长总体呈上升趋势;
(2)小亮发现大蒜是第4天开始生根,再过4天开始发芽;
(3)10÷40=。
故答案为:(1)上升;(2)4;4;(3)。
(1)、(2)观察统计图可知:蒜的根和芽在这个阶段生长总体呈上升趋势;小亮发现大蒜是第4天开始生根,再过4天开始发芽;
(3)第10天时,芽的长度是根的分率=第10天芽的长度÷根的长度。
17.(1)7;30
(2)18;12
(3)200;35
解:(1)在7日苹果的销量最低,在30日梨的销量最高。
(2)40-28=12(箱)
在18日两种水果的销量相差最大,相差了12箱。
(3)苹果:35+27+30+28+35+45=200(箱)
梨:28+35+32+40+45+55=235(箱)
235-200=35(箱)
苹果一共卖出200,比梨少35箱。
故答案为:(1)7;30;(2)18;12;(3)200;35。
(1)苹果的销量中27最小,梨的销量中55最大,据此解答;
(2)两种水果的销量之间的格数最多,说明销量相差最大,他们的差就是相差的箱数;
(3)先分别算出苹果一共卖出的箱数,梨一共卖出的箱数,再计算它们的差。
18.(1)折线
(2)2;1
(3)61.2
解:(1)这是一个折线统计图;
(2)两人在第2轮的得分相差最大,在第1轮的得分相差最小;
(3)(76.5+88+94.05+94.05+86.4)-(72+62.4+84.15+80.85+78.4)
=439-377.8
=61.2(分)
故答案为:(1)折线;(2)2;1;(3)61.2。
(1)用折线来表示数据的大小和增减变化情况,这是折线统计图;
(2)根据每个轮次两人的得分结合图形可以判断哪轮得分相差最大,哪轮得分相差最小;
(3)把两人的总得分相减即可求出相差的分数。
19.(1)9;40
(2)1
(3)56
(4)
解:(1)9时整,列车相距最远,是140-100=40(千米);
(2)10时-9时=1小时;
(3)280÷5=56(千米);
(4)280÷300=。
故答案为:(1)9;40;(2)1;(3)56;(4)。
(1)实线表示轿车,虚线表示货车,9时轿车行驶140千米,货车行驶100千米,此时两车的距离最远;
(2)从9时到10时之间是轿车在路上停留的时间;
(3)用货车行驶的路程除以时间即可求出货车平均每小时行驶的路程;
(4)货车行了280千米,轿车行了300千米,用货车行的路程除以轿车行的路程即可求出货车行驶的路程是轿车行驶路程的几分之几。
20.(1)解: 从图上可以看出,A管进水15分钟后,才打开B管。
(2)解:25-15=10(分)
50-20=30(厘米)
30÷10=3(厘米)
80×3=240(立方厘米)=240(毫升)
答:每分钟进水240毫升。
(3)解:30-25=5(分)
5×3=15(cm)
15×80=1200(mL)
答:长方体内溢出1200毫升的水。
(1)0~15分的折线时匀速向上走,15分钟的时候折线开始向上走,据此解答;
(2)A、B两管同时进水时间是10分钟,水深增加了30厘米,说明1分钟水深增加3厘米,水箱的底面积×1分钟增加的水深=每分钟进水的体积。
21.(1)答:我建议超市老板后面一段时间将乙饮料多进一些。因为乙饮料的销量呈上升趋势,甲饮料的销量呈下降趋势。
(2)解:6=2×3,4=2×2
6和4的最小公倍数是2×2×3=12
12+2=14(元)
答:刘老师带了14元。
(1)甲饮料的销量在下降,乙饮料的销量在上升,所以建议超市老板后面一段时间将乙饮料多进一些;
(2)刘老师带的钱数=6和4的最小公倍数+2元,据此解答。
22.(1)10:00
(2)解:2路车:100÷4=25(千米/时)
4路车:(千米/时)
答:2路车平均每小时行25千米;4路车平均每小时行33千米。
(3)解:9时-7时=2个小时
80-40=40(千米)
答:在4路车开出2小时,两车行驶的路程相差最多,相差40千米。
解:(1)2路车与4路车在7点半左右第一次相遇,10点钟第二次相遇。
故答案为:(1)10:00。
(1)两条线相交于一点,就说明两车相遇了;
(2)行驶的路程÷行驶的时间=行驶的速度;
(3)两条线之间的格数越多,说明相差最多,大数-小数=相差的千米数。
23.(1)15 分钟 20 厘米
(2)解:25- 15=10(分钟) 60-20= 40(厘米)
(3)解:40÷10=4(厘米)
