第三单元 圆柱与圆锥--2024-2025学年人教版六年级数学下册单元测试卷(含答案)
文档属性
| 名称 | 第三单元 圆柱与圆锥--2024-2025学年人教版六年级数学下册单元测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 373.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 18:30:48 | ||
图片预览



文档简介
第三单元 圆柱与圆锥
一、单选题
1.一个圆柱的侧面展开图是正方形,这个圆柱的高与底面半径的比是( )
A.π:1 B.π:2 C.2π:1 D.π:4
2.某工厂生产了一种圆柱形茶叶罐,尺寸如图。下面是三种茶叶罐侧面的商标纸(需贴满侧面),选( )比较合适。
A.
B.
C.
3.自来水管的内直径是2cm,水管内水的流速是每秒8cm。一位同学去洗手,走时忘记关掉水龙头,半分浪费( )mL水。
A.3.14×22×8÷2 B.3.14×12 ×8÷2
C.3.14×22×8×30 D.3.14×12×8×30
4.甲、乙两人分别用两张完全一样的长方形纸片,围成一个尽可能大的圆柱形纸筒,甲以纸片的长作为纸筒的高,乙以纸片的宽作为纸筒的高,将两人围成的圆柱形纸筒的侧面积相比较,( )。
A.甲围成的大 B.一样大 C.乙围成的大 D.无法判断
5.在学习圆柱的体积计算公式时,是把圆柱转化为( )推导出来的。
A.正方体 B.长方体 C.长方形 D.正方形
6.把一个底面半径是5cm、高8cm的圆柱切拼成一个近似的长方体(如图),圆柱的表面积比长方体的表面积,( )cm
A.多40 B.多80 C.少 40 D.少 80
7.将一个圆锥沿着它的高平均切成两块,切面一定是一个( )
A.长方形 B.等腰三角形 C.扇形 D.圆形
8.有一块正方体木料,它的棱长是2分米,把它加工成一个最大的圆柱,这个圆柱的体积是( )立方分米.
A.23.12 B.12.56 C.6.28 D.3.14
二、判断题
9.一个圆柱体木料,把它加工成最大的圆锥体,削去部分的体积和圆锥的体积比是2:1。( )
10.两个圆柱的侧面积相等,它们的高一定也相等。( )
11.圆柱的底面直径是3cm,高是9.42cm,它的侧面展开后一定是一个正方形。( )
12.将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形.( )
13.如果圆柱体积是圆锥体积的3倍,那么它们一定是等底等高。( )
三、填空题
14.一个圆柱和一个圆锥等底等高,它们的体积相差75.36 cm3。如果圆锥的底面半径是3 cm,那么这个圆锥的高是 cm。
15.一个圆柱的侧面展开图是一个正方形,这个圆柱的高是25.12 dm,那么圆柱的底面周长是 dm,底面直径是 dm。
16.把一支新的圆柱形铅笔削尖,笔尖(圆锥部分)的体积是削去部分的 。
17.如下图,把一根圆柱形木料沿底面直径竖直切成两部分,表面积比原来增加了60cm2,已知圆柱形木料的底面直径是3cm,这根圆柱形木料的体积是 cm3。
18.一个圆柱和一个圆锥的底面积相等,体积也相等。已知圆锥的高是3.6dm,圆柱的高是 dm。
19.一个圆柱的底面半径是5cm,高是10cm,侧面积是 cm2,体积是 cm3。
20.一台压路机前轮直径1.5m,轮宽4m,前轮滚动一周,压路的面积是 ㎡。
21.把一个圆柱削成最大的圆锥,削去部分的体积是25.12立方厘米,削成的圆锥体积是 立方厘米,如果这个圆柱的底面半径是1厘米,那么削成的圆锥的高是 厘米。
四、操作题
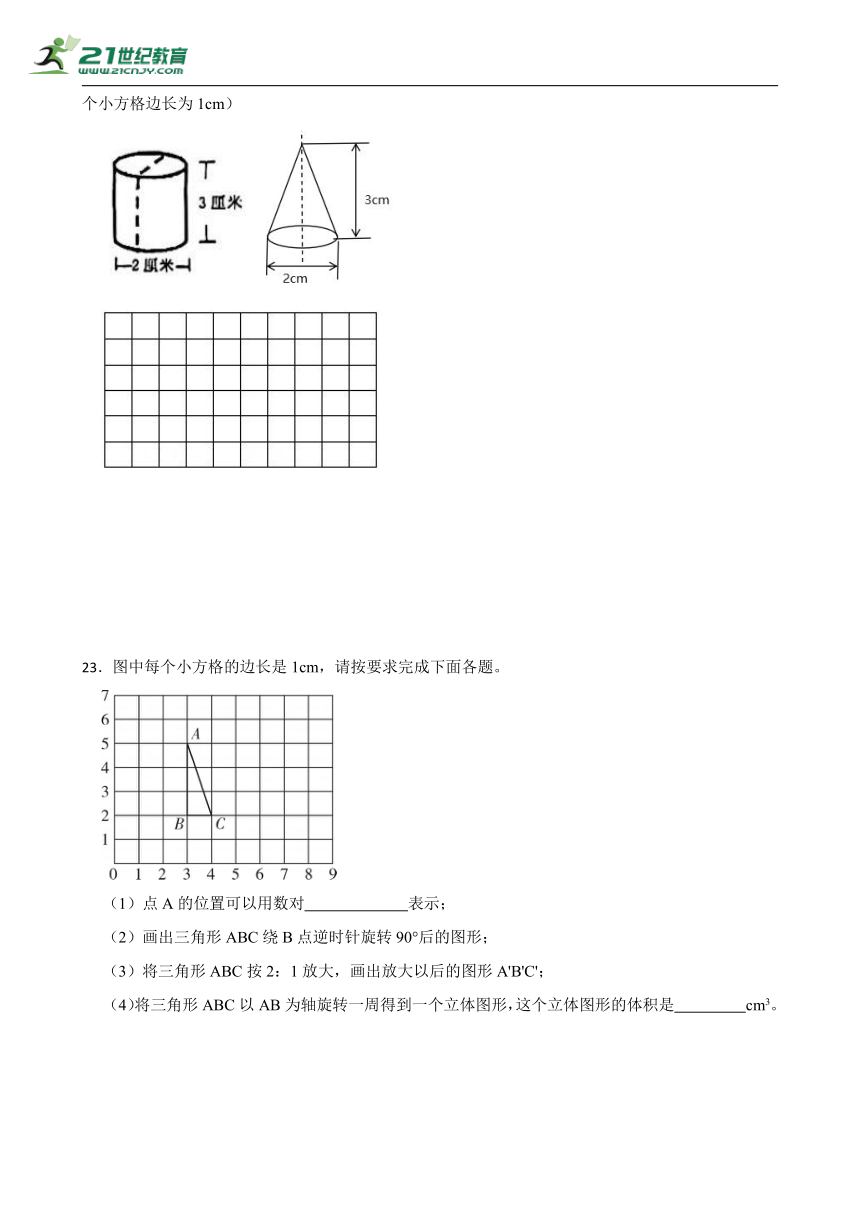
22.把下面的圆柱和圆锥沿着虚线所示切一刀,横截面分别是什么图形?画在下边的方格图中。(每个小方格边长为1cm)
23.图中每个小方格的边长是1cm,请按要求完成下面各题。
(1)点A的位置可以用数对 表示;
(2)画出三角形ABC绕B点逆时针旋转90°后的图形;
(3)将三角形ABC按2:1放大,画出放大以后的图形A'B'C';
(4)将三角形ABC以AB为轴旋转一周得到一个立体图形,这个立体图形的体积是 cm3。
24.图中每个小方格表示1cm 。
(1)按2:1在方格图中画出三角形放大后的图形,放大后三角形的面积是( )平方厘米。
(2)以BC为轴,旋转一周,形成的立体图形体积为( )立方厘米。
五、解决问题
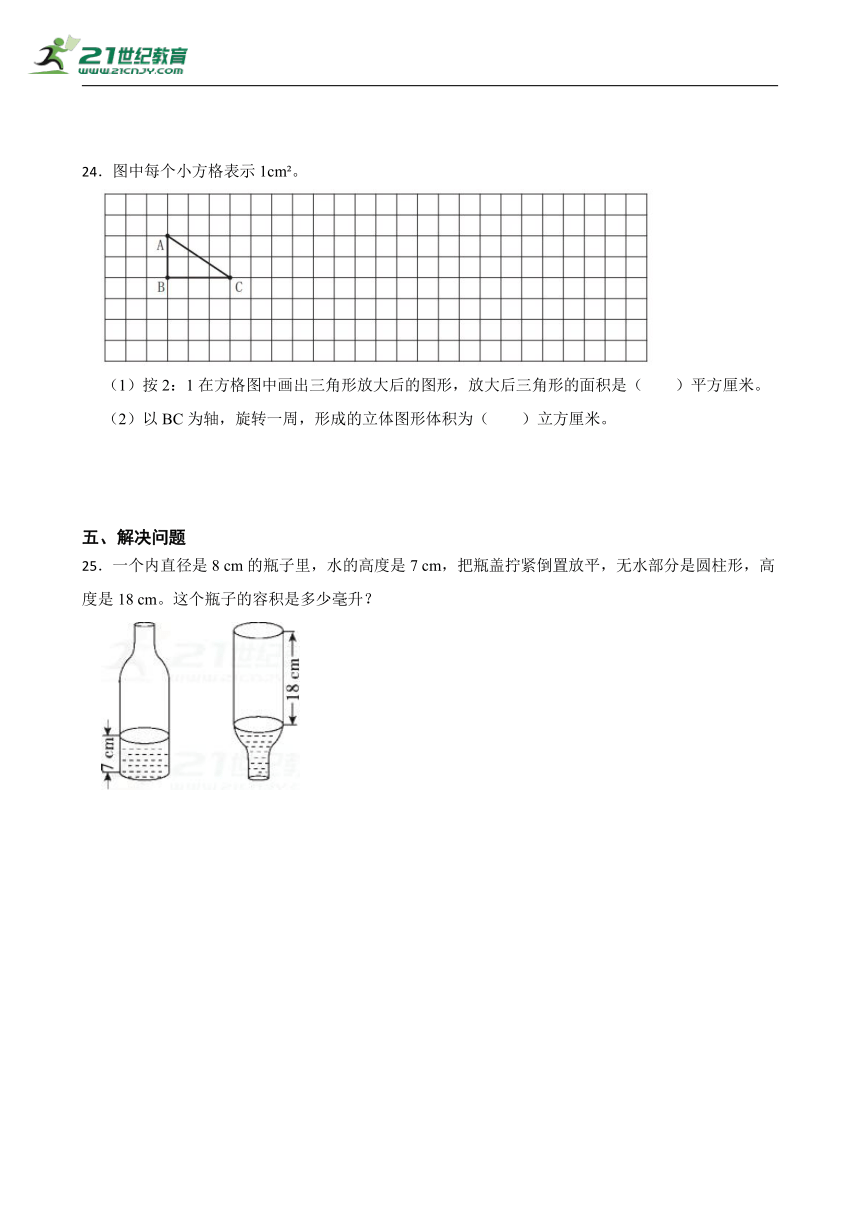
25.一个内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少毫升?
26.一个底面直径是2dm的圆柱形玻璃杯内盛有一些水,恰好占杯子容量的,现将一个铁块完全浸没在水中,水面上升了5cm,这时水面距杯口还有4 cm。这个杯子的容积是多少升?
27.一个纪念奖杯的规格如图所示,它的体积是多少立方厘米?
28.如图,两个一样的圆柱,底面直径是4cm,高是6cm,按如图所示切开,切开后一个截面的面积分别是多少平方厘米?
29.聪聪受到《乌鸦喝水》的启发,利用圆柱形容器和体积相同的10个圆锥形铁锤进行了如下实验:把10个底面半径是10 cm、高是6cm的圆锥形铁锤,浸没在底面直径是40cm的圆柱形容器的水中(水没有溢出),你知道水面上升了多少吗?
答案解析部分
1.C
解:2πr=h,所以圆柱的高与底面半径的比是2π:1。
故答案为:C。
一个圆柱的侧面展开图是正方形,说明圆柱的底面周长=圆柱的高,然后作比即可。
2.C
解:10×3.14=31.4(厘米),选择高大于或者等于16厘米,底面周长大于或者等于31.4厘米的比较合适。
故答案为:C。
这个圆柱的底面周长=π×直径,高大于或者等于16厘米的合适。
3.D
解:半分钟=30秒
2÷2=1(厘米)
3.14×12×8×30
=25.12×30
=753.6(立方厘米)
753.6立方厘米=753.6毫升。
故答案为:D。
先单位换算半分钟=30秒,半分浪费水的体积=π×半径2×水的流速×时间。
4.B
解:两人围成的圆柱形纸筒的侧面积相等,都是这张长方形纸片的面积。
故答案为:B。
把长方形围成圆柱体,侧面积等于长方形纸片的面积。
5.B
解:在学习圆柱的体积计算公式时,是把圆柱转化为长方体推导出来的。
故答案为:B。
把圆柱转化成长方体,长方体的体积=底面积×高,从而推导出圆柱的体积=底面积×高。
6.D
解:8×5×2=80(平方厘米),圆柱的表面积比长方体的表面积少80平方厘米。
故答案为:D。
拼成近似长方体后,表面积会增加左右两个面的面积,每个面的长是圆柱的底面半径,宽是圆柱的高,由此计算这两个面的面积就是两个图形表面积相差的部分。
7.B
解:圆锥的侧面展开是一个扇形,将一个圆锥沿着它的高平均切成两块,切面一定是一个等腰三角形。
故答案为:B。
依据圆锥的特征可知:圆锥沿着它的高平均切成两块,切面一定是一个等腰三角形。
8.C
解:3.14×(2÷2) ×2
=3.14×2
=6.28(立方分米)
故答案为:C。
正方体木料加工成的最大的圆柱的底面直径和高与正方体的棱长相等。圆柱的体积=底面积×高,根据公式计算体积即可。
9.正确
解:2:(3-2)=2:1。
故答案为:正确。
等底等高的圆柱的体积是圆锥体积的3倍,把这个圆柱的体积看作3份,这个圆锥的体积是1份,削去部分的体积和圆锥的体积比=2:(3-2)=2:1。
10.错误
解:两个圆柱的侧面积相等,侧面积的大小是由底面周长和高两个因素共同决定的。因此,如果两个圆柱的侧面积相等,并不意味着它们的底面周长和高也一定相等。实际上,只要底面周长和高的乘积相等,两个圆柱的侧面积就可以相等。
故答案为:错误。
圆柱的侧面积=底面周长×高,底面周长=π×直径,圆柱的侧面积与底面半径和高有关。
11.错误
解:3.14×3=9.42(厘米),这个圆柱沿高剪开后是正方形,原题干说法错误。
故答案为:错误。
圆柱的底面周长=π×直径=圆柱的高,只有这个圆柱沿高剪开后是正方形。
12.正确
解:将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形。原题说法正确。
故答案为:正确。
圆柱的底面周长和高不相等,圆柱的侧面沿着高展开后就是长方形;底面周长和高相等,圆柱的侧面展开后就是正方形;如果沿着侧面斜着展开后就是平行四边形。
13.错误
解:假设圆柱体积是12,则圆锥体积是4,
圆柱底面积和高可以分别是4和3,
圆锥的底面积和高可以分别是6和2,
那么圆柱和圆锥就不是等底等高;
所以圆柱体积是圆锥体积的3倍,这两者不一定是等底等高,原说法错误;
故答案为:错误。
由圆柱和圆锥的体积公式可知,它们的体积是由底面积和高乘积决定的,如果圆柱体积是圆锥体积的3倍,那么它们的底面积与高的乘积就相等,但不一定等底等高,由此即可得答案。
14.4
解:等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍,
圆锥的体积:75.36÷(3-1)=75.36÷2=37.68(立方厘米)
圆锥的高:37.68×3÷(3.14×3×3)=113.04÷28.26=4(厘米)
故答案为:4。
差倍问题:差÷(倍数-1)=较小数;较小数就是圆锥的体积;圆锥的体积×3÷圆锥的底面积=圆锥的高。
15.25.12;8
解:一个圆柱的侧面展开图是一个正方形,说明这个圆柱的底面周长和高相等,
这个圆柱的高是25.12 dm,那么圆柱的底面周长是25.12dm,
25.12÷3.14=8(dm),底面直径是8dm。
故答案为:25.12;8。
底面周长÷π=底面直径,据此解答。
16.
解:1÷(3-1)
=1÷2
=。
故答案为:。
等底等高的圆柱的体积是圆锥体积的3倍,笔尖(圆锥部分)的体积是削去部分的。
17.70.65
解:60÷2÷3
=30÷3
=10(厘米)
3÷2=1.5(厘米)
3.14×1.52×10
=7.065×10
=70.65(立方厘米)。
故答案为:70.65。
这根圆柱形木料的体积=底面积×高;其中,底面积=π×半径2, 半径=直径÷2,高=增加的表面积÷增加面的个数÷底面直径。
18.1.2
解:3.6÷3=1.2(分米)。
故答案为:1.2。
等底等高的圆柱的体积是圆锥体积的3倍,圆柱的高=这个圆锥的高÷3。
19.314;785
解:5×2×3.14×10
=10×3.14×10
=31.4×10
=314(平方厘米)
3.14×52×10
=78.5×10
=785(立方厘米)。
故答案为:314;785。
圆柱的侧面积=底面周长×高;圆柱的体积=底面积×高;其中,底面积=π×半径2。
20.18.84
解:3.14×1.5×4
=4.71×4
=18.84(平方米)。
故答案为:18.84。
压路的面积=压路机的侧面积=π×直径×高。
21.12.56;12
解:25.12÷2=12.56(立方厘米),所以削成的圆锥体积是12.56立方厘米;
12×3.14=3.14(平方厘米),12.56÷÷3.14=12(厘米),所以削成的圆锥的高是12厘米。
故答案为:12.56;12。
把圆柱削成最大的圆锥,圆柱和圆锥等底等高,圆柱的体积是圆锥的3倍,所以削成的圆锥体积=削去部分的体积÷2;
圆锥的底面积=πr2,所以削成的圆锥的高=圆锥的体积÷÷底面积。
22.解:
沿着虚线切开,分别是长3厘米,宽2厘米的长方形;底2厘米,高3厘米的等腰三角形。
23.(1)(3,5)
(2)解:
(3)解:
(4)3.14
解:(1)点A的位置可以用数对(3,5)表示;
(2)3.14×12×3÷3
=3.14×(3÷3)
=3.14×1
=3.14(立方厘米)。
故答案为:(1)(3,5);(2)3.14。
(1)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;
(2)作旋转图形的方法:图形的旋转的关键是旋转中心、旋转方向和旋转的角度;画图时先弄清楚旋转的方向和角度,再确定从旋转点出发的两条线段旋转后的位置,这是关键所在,最后画其他的线段即可;
(3)放大后三角形底、高的格数分别=原来三角形底、高的格数分别×2;
(4)这个立体图形的体积=π×半径2×高÷3。
24.(1)解:6×4÷2=24÷2=12(平方厘米)
放大后三角形的面积是12平方厘米。
(2)解:形成的圆锥底面半径是3厘米,高是2厘米,
体积是3.14×3×3×2÷3
=28.26×2÷3
=56.52÷3
=18.84(立方厘米)
形成的立体图形体积为18.84立方厘米。
(1)原三角形的两条直角边×2=放大后的三角形的两条直角边,据此作图;
(2)圆锥的体积=π×底面半径的平方×高÷3。
25.解:3.14×(8÷2)2×(7+18)=1256(cm3)=1256 mL
答:这个瓶子的容积是1256 mL。
由题可知,水的体积相当于一个底面为瓶子底面、高是7cm的圆柱的体积,剩余部分的体积相当于一个底面为瓶子底面、高是18cm的圆柱的体积。瓶子的容积=两个圆柱的体积之和=瓶子的底面积×高之和。
26.解:2dm=20cm
3.14×(20÷2)2×(5+4)÷(1-)
=3.14×100×9÷
=314×9÷
=2826÷
=4710(cm3)
4710 cm3=4.71L
答:这个杯子的容积是4.71L。
先把单位进行换算,即2dm=20cm,原来杯子中的水到杯口的距离=铁块完全浸没在水中水上升的高度+放入铁块后水面距杯口的距离,那么杯子的高=原来杯子中的水到杯口的距离÷(1-原来水占杯子容量的几分之几),所以这个杯子的容积=π×(直径÷2)2×高,据此作答即可。
27.解:3.14×(8÷2)2×(14+20)÷2
=50.24×34÷2
=1708.16÷2
=854.08(cm3)
答:它的体积是854.08cm3。
从图中可以看出,两个同样的纪念奖杯可以拼成一个高为(14+20)cm的圆柱,那么这个纪念品的体积=(底面直径÷2)2×π×两个纪念品拼在一起的高÷2,据此代入数值作答即可。
28.解:4×6=24(cm2)
3.14×(4÷2)2
=3.14×4
=12.56(cm2)
答:切开后一个截面的面积分别是24cm2、12.56cm2。
观察图,竖着切,截面是一个长方形,长是圆柱的高,宽是圆柱的底面直径;横着切,截面和圆柱的底面相同,直径是4cm,根据圆的面积公式计算即可。
29.解:×3.14×102×6×10÷[3.14×()2]
=6280÷1256
=5(cm)
答:水面上升了5cm。
水面上升的高度=π×半径2×高×个数÷3÷(π×半径2)。
一、单选题
1.一个圆柱的侧面展开图是正方形,这个圆柱的高与底面半径的比是( )
A.π:1 B.π:2 C.2π:1 D.π:4
2.某工厂生产了一种圆柱形茶叶罐,尺寸如图。下面是三种茶叶罐侧面的商标纸(需贴满侧面),选( )比较合适。
A.
B.
C.
3.自来水管的内直径是2cm,水管内水的流速是每秒8cm。一位同学去洗手,走时忘记关掉水龙头,半分浪费( )mL水。
A.3.14×22×8÷2 B.3.14×12 ×8÷2
C.3.14×22×8×30 D.3.14×12×8×30
4.甲、乙两人分别用两张完全一样的长方形纸片,围成一个尽可能大的圆柱形纸筒,甲以纸片的长作为纸筒的高,乙以纸片的宽作为纸筒的高,将两人围成的圆柱形纸筒的侧面积相比较,( )。
A.甲围成的大 B.一样大 C.乙围成的大 D.无法判断
5.在学习圆柱的体积计算公式时,是把圆柱转化为( )推导出来的。
A.正方体 B.长方体 C.长方形 D.正方形
6.把一个底面半径是5cm、高8cm的圆柱切拼成一个近似的长方体(如图),圆柱的表面积比长方体的表面积,( )cm
A.多40 B.多80 C.少 40 D.少 80
7.将一个圆锥沿着它的高平均切成两块,切面一定是一个( )
A.长方形 B.等腰三角形 C.扇形 D.圆形
8.有一块正方体木料,它的棱长是2分米,把它加工成一个最大的圆柱,这个圆柱的体积是( )立方分米.
A.23.12 B.12.56 C.6.28 D.3.14
二、判断题
9.一个圆柱体木料,把它加工成最大的圆锥体,削去部分的体积和圆锥的体积比是2:1。( )
10.两个圆柱的侧面积相等,它们的高一定也相等。( )
11.圆柱的底面直径是3cm,高是9.42cm,它的侧面展开后一定是一个正方形。( )
12.将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形.( )
13.如果圆柱体积是圆锥体积的3倍,那么它们一定是等底等高。( )
三、填空题
14.一个圆柱和一个圆锥等底等高,它们的体积相差75.36 cm3。如果圆锥的底面半径是3 cm,那么这个圆锥的高是 cm。
15.一个圆柱的侧面展开图是一个正方形,这个圆柱的高是25.12 dm,那么圆柱的底面周长是 dm,底面直径是 dm。
16.把一支新的圆柱形铅笔削尖,笔尖(圆锥部分)的体积是削去部分的 。
17.如下图,把一根圆柱形木料沿底面直径竖直切成两部分,表面积比原来增加了60cm2,已知圆柱形木料的底面直径是3cm,这根圆柱形木料的体积是 cm3。
18.一个圆柱和一个圆锥的底面积相等,体积也相等。已知圆锥的高是3.6dm,圆柱的高是 dm。
19.一个圆柱的底面半径是5cm,高是10cm,侧面积是 cm2,体积是 cm3。
20.一台压路机前轮直径1.5m,轮宽4m,前轮滚动一周,压路的面积是 ㎡。
21.把一个圆柱削成最大的圆锥,削去部分的体积是25.12立方厘米,削成的圆锥体积是 立方厘米,如果这个圆柱的底面半径是1厘米,那么削成的圆锥的高是 厘米。
四、操作题
22.把下面的圆柱和圆锥沿着虚线所示切一刀,横截面分别是什么图形?画在下边的方格图中。(每个小方格边长为1cm)
23.图中每个小方格的边长是1cm,请按要求完成下面各题。
(1)点A的位置可以用数对 表示;
(2)画出三角形ABC绕B点逆时针旋转90°后的图形;
(3)将三角形ABC按2:1放大,画出放大以后的图形A'B'C';
(4)将三角形ABC以AB为轴旋转一周得到一个立体图形,这个立体图形的体积是 cm3。
24.图中每个小方格表示1cm 。
(1)按2:1在方格图中画出三角形放大后的图形,放大后三角形的面积是( )平方厘米。
(2)以BC为轴,旋转一周,形成的立体图形体积为( )立方厘米。
五、解决问题
25.一个内直径是8 cm的瓶子里,水的高度是7 cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18 cm。这个瓶子的容积是多少毫升?
26.一个底面直径是2dm的圆柱形玻璃杯内盛有一些水,恰好占杯子容量的,现将一个铁块完全浸没在水中,水面上升了5cm,这时水面距杯口还有4 cm。这个杯子的容积是多少升?
27.一个纪念奖杯的规格如图所示,它的体积是多少立方厘米?
28.如图,两个一样的圆柱,底面直径是4cm,高是6cm,按如图所示切开,切开后一个截面的面积分别是多少平方厘米?
29.聪聪受到《乌鸦喝水》的启发,利用圆柱形容器和体积相同的10个圆锥形铁锤进行了如下实验:把10个底面半径是10 cm、高是6cm的圆锥形铁锤,浸没在底面直径是40cm的圆柱形容器的水中(水没有溢出),你知道水面上升了多少吗?
答案解析部分
1.C
解:2πr=h,所以圆柱的高与底面半径的比是2π:1。
故答案为:C。
一个圆柱的侧面展开图是正方形,说明圆柱的底面周长=圆柱的高,然后作比即可。
2.C
解:10×3.14=31.4(厘米),选择高大于或者等于16厘米,底面周长大于或者等于31.4厘米的比较合适。
故答案为:C。
这个圆柱的底面周长=π×直径,高大于或者等于16厘米的合适。
3.D
解:半分钟=30秒
2÷2=1(厘米)
3.14×12×8×30
=25.12×30
=753.6(立方厘米)
753.6立方厘米=753.6毫升。
故答案为:D。
先单位换算半分钟=30秒,半分浪费水的体积=π×半径2×水的流速×时间。
4.B
解:两人围成的圆柱形纸筒的侧面积相等,都是这张长方形纸片的面积。
故答案为:B。
把长方形围成圆柱体,侧面积等于长方形纸片的面积。
5.B
解:在学习圆柱的体积计算公式时,是把圆柱转化为长方体推导出来的。
故答案为:B。
把圆柱转化成长方体,长方体的体积=底面积×高,从而推导出圆柱的体积=底面积×高。
6.D
解:8×5×2=80(平方厘米),圆柱的表面积比长方体的表面积少80平方厘米。
故答案为:D。
拼成近似长方体后,表面积会增加左右两个面的面积,每个面的长是圆柱的底面半径,宽是圆柱的高,由此计算这两个面的面积就是两个图形表面积相差的部分。
7.B
解:圆锥的侧面展开是一个扇形,将一个圆锥沿着它的高平均切成两块,切面一定是一个等腰三角形。
故答案为:B。
依据圆锥的特征可知:圆锥沿着它的高平均切成两块,切面一定是一个等腰三角形。
8.C
解:3.14×(2÷2) ×2
=3.14×2
=6.28(立方分米)
故答案为:C。
正方体木料加工成的最大的圆柱的底面直径和高与正方体的棱长相等。圆柱的体积=底面积×高,根据公式计算体积即可。
9.正确
解:2:(3-2)=2:1。
故答案为:正确。
等底等高的圆柱的体积是圆锥体积的3倍,把这个圆柱的体积看作3份,这个圆锥的体积是1份,削去部分的体积和圆锥的体积比=2:(3-2)=2:1。
10.错误
解:两个圆柱的侧面积相等,侧面积的大小是由底面周长和高两个因素共同决定的。因此,如果两个圆柱的侧面积相等,并不意味着它们的底面周长和高也一定相等。实际上,只要底面周长和高的乘积相等,两个圆柱的侧面积就可以相等。
故答案为:错误。
圆柱的侧面积=底面周长×高,底面周长=π×直径,圆柱的侧面积与底面半径和高有关。
11.错误
解:3.14×3=9.42(厘米),这个圆柱沿高剪开后是正方形,原题干说法错误。
故答案为:错误。
圆柱的底面周长=π×直径=圆柱的高,只有这个圆柱沿高剪开后是正方形。
12.正确
解:将圆柱的侧面展开有可能是长方形,也有可能是正方形,还有可能是平行四边形。原题说法正确。
故答案为:正确。
圆柱的底面周长和高不相等,圆柱的侧面沿着高展开后就是长方形;底面周长和高相等,圆柱的侧面展开后就是正方形;如果沿着侧面斜着展开后就是平行四边形。
13.错误
解:假设圆柱体积是12,则圆锥体积是4,
圆柱底面积和高可以分别是4和3,
圆锥的底面积和高可以分别是6和2,
那么圆柱和圆锥就不是等底等高;
所以圆柱体积是圆锥体积的3倍,这两者不一定是等底等高,原说法错误;
故答案为:错误。
由圆柱和圆锥的体积公式可知,它们的体积是由底面积和高乘积决定的,如果圆柱体积是圆锥体积的3倍,那么它们的底面积与高的乘积就相等,但不一定等底等高,由此即可得答案。
14.4
解:等底等高的圆柱和圆锥,圆柱的体积是圆锥体积的3倍,
圆锥的体积:75.36÷(3-1)=75.36÷2=37.68(立方厘米)
圆锥的高:37.68×3÷(3.14×3×3)=113.04÷28.26=4(厘米)
故答案为:4。
差倍问题:差÷(倍数-1)=较小数;较小数就是圆锥的体积;圆锥的体积×3÷圆锥的底面积=圆锥的高。
15.25.12;8
解:一个圆柱的侧面展开图是一个正方形,说明这个圆柱的底面周长和高相等,
这个圆柱的高是25.12 dm,那么圆柱的底面周长是25.12dm,
25.12÷3.14=8(dm),底面直径是8dm。
故答案为:25.12;8。
底面周长÷π=底面直径,据此解答。
16.
解:1÷(3-1)
=1÷2
=。
故答案为:。
等底等高的圆柱的体积是圆锥体积的3倍,笔尖(圆锥部分)的体积是削去部分的。
17.70.65
解:60÷2÷3
=30÷3
=10(厘米)
3÷2=1.5(厘米)
3.14×1.52×10
=7.065×10
=70.65(立方厘米)。
故答案为:70.65。
这根圆柱形木料的体积=底面积×高;其中,底面积=π×半径2, 半径=直径÷2,高=增加的表面积÷增加面的个数÷底面直径。
18.1.2
解:3.6÷3=1.2(分米)。
故答案为:1.2。
等底等高的圆柱的体积是圆锥体积的3倍,圆柱的高=这个圆锥的高÷3。
19.314;785
解:5×2×3.14×10
=10×3.14×10
=31.4×10
=314(平方厘米)
3.14×52×10
=78.5×10
=785(立方厘米)。
故答案为:314;785。
圆柱的侧面积=底面周长×高;圆柱的体积=底面积×高;其中,底面积=π×半径2。
20.18.84
解:3.14×1.5×4
=4.71×4
=18.84(平方米)。
故答案为:18.84。
压路的面积=压路机的侧面积=π×直径×高。
21.12.56;12
解:25.12÷2=12.56(立方厘米),所以削成的圆锥体积是12.56立方厘米;
12×3.14=3.14(平方厘米),12.56÷÷3.14=12(厘米),所以削成的圆锥的高是12厘米。
故答案为:12.56;12。
把圆柱削成最大的圆锥,圆柱和圆锥等底等高,圆柱的体积是圆锥的3倍,所以削成的圆锥体积=削去部分的体积÷2;
圆锥的底面积=πr2,所以削成的圆锥的高=圆锥的体积÷÷底面积。
22.解:
沿着虚线切开,分别是长3厘米,宽2厘米的长方形;底2厘米,高3厘米的等腰三角形。
23.(1)(3,5)
(2)解:
(3)解:
(4)3.14
解:(1)点A的位置可以用数对(3,5)表示;
(2)3.14×12×3÷3
=3.14×(3÷3)
=3.14×1
=3.14(立方厘米)。
故答案为:(1)(3,5);(2)3.14。
(1)用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;
(2)作旋转图形的方法:图形的旋转的关键是旋转中心、旋转方向和旋转的角度;画图时先弄清楚旋转的方向和角度,再确定从旋转点出发的两条线段旋转后的位置,这是关键所在,最后画其他的线段即可;
(3)放大后三角形底、高的格数分别=原来三角形底、高的格数分别×2;
(4)这个立体图形的体积=π×半径2×高÷3。
24.(1)解:6×4÷2=24÷2=12(平方厘米)
放大后三角形的面积是12平方厘米。
(2)解:形成的圆锥底面半径是3厘米,高是2厘米,
体积是3.14×3×3×2÷3
=28.26×2÷3
=56.52÷3
=18.84(立方厘米)
形成的立体图形体积为18.84立方厘米。
(1)原三角形的两条直角边×2=放大后的三角形的两条直角边,据此作图;
(2)圆锥的体积=π×底面半径的平方×高÷3。
25.解:3.14×(8÷2)2×(7+18)=1256(cm3)=1256 mL
答:这个瓶子的容积是1256 mL。
由题可知,水的体积相当于一个底面为瓶子底面、高是7cm的圆柱的体积,剩余部分的体积相当于一个底面为瓶子底面、高是18cm的圆柱的体积。瓶子的容积=两个圆柱的体积之和=瓶子的底面积×高之和。
26.解:2dm=20cm
3.14×(20÷2)2×(5+4)÷(1-)
=3.14×100×9÷
=314×9÷
=2826÷
=4710(cm3)
4710 cm3=4.71L
答:这个杯子的容积是4.71L。
先把单位进行换算,即2dm=20cm,原来杯子中的水到杯口的距离=铁块完全浸没在水中水上升的高度+放入铁块后水面距杯口的距离,那么杯子的高=原来杯子中的水到杯口的距离÷(1-原来水占杯子容量的几分之几),所以这个杯子的容积=π×(直径÷2)2×高,据此作答即可。
27.解:3.14×(8÷2)2×(14+20)÷2
=50.24×34÷2
=1708.16÷2
=854.08(cm3)
答:它的体积是854.08cm3。
从图中可以看出,两个同样的纪念奖杯可以拼成一个高为(14+20)cm的圆柱,那么这个纪念品的体积=(底面直径÷2)2×π×两个纪念品拼在一起的高÷2,据此代入数值作答即可。
28.解:4×6=24(cm2)
3.14×(4÷2)2
=3.14×4
=12.56(cm2)
答:切开后一个截面的面积分别是24cm2、12.56cm2。
观察图,竖着切,截面是一个长方形,长是圆柱的高,宽是圆柱的底面直径;横着切,截面和圆柱的底面相同,直径是4cm,根据圆的面积公式计算即可。
29.解:×3.14×102×6×10÷[3.14×()2]
=6280÷1256
=5(cm)
答:水面上升了5cm。
水面上升的高度=π×半径2×高×个数÷3÷(π×半径2)。
