第一单元 圆柱和圆锥单元常考易错卷(基础卷)(含答案)北师大版数学六年级下册
文档属性
| 名称 | 第一单元 圆柱和圆锥单元常考易错卷(基础卷)(含答案)北师大版数学六年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-22 20:47:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第一单元 圆柱和圆锥单元常考易错卷(基础卷)
北师大版数学 六年级下册
一、填空题
1.圆柱上下面是两个 的圆形,有 个面是弯曲的;圆锥的底面是一个 形,侧面是一个 面。
2.把圆柱的 展开可以得到一个长方形,这个长方形的长等于圆柱的 ,宽等于圆柱的 。
3. 一个底面半径3cm,高7cm的圆柱的侧面沿高剪开得到一个长方形,这个长方形的长是 cm,宽是 cm。
4.把一张边长是40厘米的正方形纸片,卷成一个最大的圆柱形纸筒。它的底面周长是 厘米,高是 厘米。
5.如图是一个圆柱的表面展开图,这个圆柱的侧面积是 cm2,表面积是 cm2。
6.一个圆锥的体积是81立方厘米,底面积是27平方厘米,它的高是 厘米。
7.一个圆柱和一个圆锥等底等高,圆锥的体积是38.4立方厘米,圆柱的体积比圆锥的体积多 立方厘米。
8.圆柱的底面半径扩大3倍,高不变,它的侧面积扩大 倍,它的体积扩大 倍,它的底面积扩大 倍。
9.一段体积是52.8立方厘米的圆柱形木料,切削成一个最大的圆锥,削去部分的体积是 立方厘米。
10.一个圆锥形容器盛满水,水深为18厘米,将圆锥形容器的水倒入和它等底等高的圆柱形容器中,水深为 厘米。
二、单选题
11.在下图中,以直线为旋转轴 ,可以得到圆柱的是( )。
A. B. C. D.
12.把一个圆锥沿底面直径到顶点切开,切面是一个( )。
A.圆形 B.三角形 C.扇形 D.无法确定
13.把一个圆柱形罐头盒的侧面打开,得到一个正方形。这个圆柱形罐头盒的底面半径是10cm,高是( )cm。
A.20 B.31.4 C.62.8 D.3140
14.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12立方分米,圆柱的体积是()立方分米。
A.12 B.36 C.4 D.8
15.如图,长方形的长是 4 cm,宽是 2 cm,分别以长边和宽边所在的直线为轴,旋转一周可以得到两个不同的圆柱。这两个圆柱的体积相比较,( )。
A.甲大 B.乙大 C.同样大 D.无法判断
三、判断题
16.圆柱的上、下底面都是圆,且大小一样。( )
17.从圆锥的顶点到底面圆周上任意一点的距离是圆锥的高。( )
18.长方体、正方体、圆柱和圆锥的体积都可以用“底面积×高”计算。
19.圆锥的体积等于圆柱体积的 。( )
20.如果两个圆柱的侧面积相等,那么它们的底面周长也一定相等。( )
四、计算题
21.计算圆柱的表面积。(单位:厘米)
22.求下面图形的体积。(单位:cm)
(1)
(2)
五、解决问题
23.一个圆柱形石墩,底面周长是94.2cm,高是20cm。这个石墩的侧面积是多少平方厘米?
24.工人李师傅用一块长90cm、宽31.4cm的铁皮焊接一节长90cm的圆柱体烟囱,这节烟囱的底面直径是多少
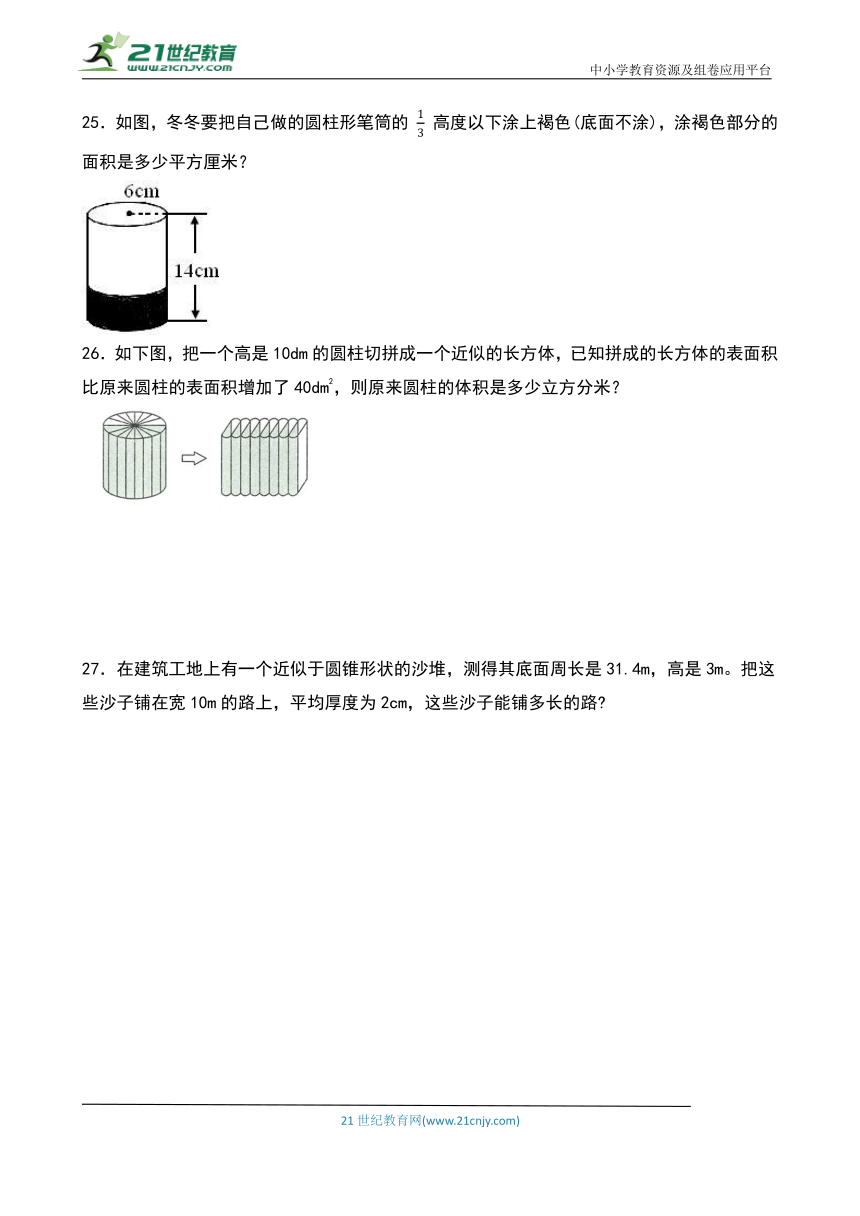
25.如图,冬冬要把自己做的圆柱形笔筒的 高度以下涂上褐色(底面不涂),涂褐色部分的面积是多少平方厘米?
26.如下图,把一个高是10dm的圆柱切拼成一个近似的长方体,已知拼成的长方体的表面积比原来圆柱的表面积增加了40dm2,则原来圆柱的体积是多少立方分米?
27.在建筑工地上有一个近似于圆锥形状的沙堆,测得其底面周长是31.4m,高是3m。把这些沙子铺在宽10m的路上,平均厚度为2cm,这些沙子能铺多长的路
答案解析部分
1.【答案】相同;1;圆;扇形
【解答】解:圆柱的上下面是两个相同的圆形,有1个面是弯曲的;圆锥的底面是一个圆形,侧面是一个扇形。
故答案为:相同;1;圆;扇形。
【分析】圆柱是上下两个面是相同的圆形,圆柱的侧面是一个曲面,沿着一条高展开后是一个长方形;圆锥的底面是一个圆形,侧面展开后是一个扇形。
2.【答案】侧面;底面周长(高);高(底面周长)
【解答】解:把圆柱的侧面展开可以得到一个长方形,这个长方形的长等于圆柱的底面周长(高),宽等于圆柱的高(底面周长)。
故答案为:侧面; 底面周长(高); 高(底面周长)。
【分析】圆柱的侧面沿高展开是一个长方形,长方形的长相当于圆柱底面周长,宽相当于圆柱的高;当底面周长和高相等时,就得到一个正方形,正方形的边长相当于圆柱的底面周长和高;斜着剪开得到一个平行四边形,平行四边形的底相当于圆柱底面周长,高相当于圆柱的高。
3.【答案】18.84;7
【解答】解:长:3.14×2×3
=6.28×3
=18.84(cm);
宽是7厘米;
故答案为:18.84;7。
【分析】展开得到的长方形的长就是圆柱的底面周长,底面周长=π×2×半径,宽就是圆柱的高,据此解答。
4.【答案】40;40
【解答】正方形卷成最大的圆柱可知,圆柱的底面周长和圆柱的高都等于正方形的边长,正方形的边长=40厘米,则圆柱的底面周长和圆柱的高也是都是40厘米。
故答案为:40;40。
【分析】根据圆柱的侧面展开图,卷成的圆柱的侧面展开是一个正方形,则正方形的一条边长是圆柱的底面周长,另一条相邻的边长是圆柱的高,题目已经告知正方形的边长,则圆柱的底面周长和圆柱的高就可以得出。
5.【答案】251.2;351.68
【解答】解:25.12×10=251.2(平方厘米)
25.12÷3.14÷2=4(厘米)
3.14×4×4=50.24(平方厘米)
50.24×2+251.2=100.48+251.2=351.68(平方厘米)
故答案为:251.2;351.68。
【分析】底面周长×高=侧面积;底面周长÷π÷2=底面半径,π×底面半径的平方=底面积;圆柱的底面积×2+圆柱的侧面积=圆柱的表面积。
6.【答案】9
【解答】81×3÷27
=243÷27
=9(厘米)
故答案为:9.
【分析】根据圆锥的体积公式:V=Sh,已知圆锥的体积和底面积,求圆锥的高,用圆锥的体积×3÷圆锥的底面积=圆锥的高,据此列式解答.
7.【答案】76.8
【解答】38.4×(3-1)
=38.4×2
=76.8(立方厘米)
故答案为:76.8。
【分析】 一个圆柱和一个圆锥等底等高,圆柱的体积是圆锥体积的3倍,圆柱的体积比圆锥体积多圆锥体积的(3-1)倍,据此列式解答.
8.【答案】3;9;9
【解答】解:圆柱的底面半径扩大3倍,高不变,它的侧面积扩大3倍,它的体积扩大9倍,它的底面积扩大9倍。
故答案为:3;9;9。
【分析】圆柱的高不变,底面半径扩大几倍,相应地,侧面积就扩大几倍,体积扩大几2倍,底面积扩大几2倍。
9.【答案】35.2
【解答】将圆柱形木料切削成一个最大的圆锥,这个圆锥是与它等底等高的圆锥,此时圆锥的体积=圆柱的体积×,所以削去部分的体积为52.8-52.8×=35.2(立方厘米)。
故答案为:35.2.
【分析】圆柱形木料切削成一个最大的圆锥,这个圆锥是与它等底等高的圆锥,圆锥的体积=圆柱的体积×。
10.【答案】6
【解答】当圆柱和圆锥的底面积和体积相等时,高之比为1:3,则在该题中,圆柱中水的高度为6厘米。
故答案为:6.
【分析】根据等底等高的圆柱体积是圆锥体积的3倍可知,体积和底面积相等的圆柱和圆锥,圆柱的高是圆锥高的,据此解答.
11.【答案】A
【解答】在下图中,以直线为旋转轴,可以得到圆柱的是.
故答案为:A.
【分析】根据对圆柱特征的理解可知,一个长方形以长或宽为旋转轴,旋转一周形成的图形是圆柱体,据此解答.
12.【答案】B
【解答】解:把一个圆锥沿底面直径到顶点切开,切面是一个三角形.
故答案为:B
【分析】圆锥是一个圆形的底面和一个曲面组成的,曲面展开后是一个扇形,根据圆锥的特征可知把一个圆锥沿底面直径到顶点切开,切面是一个三角形.
13.【答案】C
【解答】解:3.14×10×2=62.8(cm)。
故答案为:C。
【分析】圆柱的底面周长和高相等时,圆柱的侧面展开后才是正方形。根据圆周长公式计算出底面周长,也就是高。
14.【答案】A
解答:由题意,底面直径相等,所以半径也相等,设圆柱和圆锥的体积分别是 , ,圆锥的体积是12立方分米,所以圆柱的体积也是12立方分米。
分析:由圆柱的体积和圆锥的体积公式。
15.【答案】B
【解答】解:甲形成的圆柱,底面半径是2厘米,高是4厘米,
体积:π×2×2×4=16π,
乙形成的圆柱,底面半径是4厘米,高是2厘米,
体积:π×4×4×2=32π,
这两个圆柱的体积相比较,乙大 。
故答案为:B。
【分析】π×底面半径的平方×高=圆柱的体积;据此先计算,再比较。
16.【答案】正确
【解答】解:圆柱的上、下底面都是圆,且大小一样。原题说法正确。
故答案为:正确。
【分析】圆柱的上、下两个面是完全相同的两个圆形。
17.【答案】错误
【解答】解:从圆锥的顶点到底面圆心的距离是圆锥的高。原题说法错误。
故答案为:错误。
【分析】圆锥只有一条高,是圆锥顶点到底面圆心的距离。
18.【答案】错误
【解答】解:长方体、正方体、圆柱可以用“底面积×高”计算,圆锥的体积=底面积×高×。原题说法错误。
故答案为:错误。
【分析】长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,长×宽是长方体的底面积,棱长×棱长是正方体的底面积;圆柱的体积=底面积×高,圆锥的体积=底面积×高×。
19.【答案】错误
【解答】解:圆锥的体积等于与之等底等高的圆柱体积的。
故答案为:错误。
【分析】圆锥的体积等于与之等底等高的圆柱体积的
20.【答案】错误
【解答】根据分析得:圆柱的侧面积与底面周长、高两个条件相关。
所以 如果两个圆柱的侧面积相等,那么它们的底面周长不一定相等。
故答案为:错误。
【分析】 因为圆柱的侧面积=底面周长×高,若两个圆柱的侧面积相等,但底面周长和高不一定相等,所以它们的底面周长不一定相等。据此判断。
21.【答案】解:2÷2=1(厘米)
3.14×12×2+3.14×2×0.8
=6.28+5.024
=11.304(厘米)
【分析】圆柱的表面积=底面积×2+侧面积;侧面积=底面周长×高。
22.【答案】(1)(6÷2)2×3.14×6×
=9×3.14×2
=28.26×2
=56.52(cm3)
(2)(8÷2)2×3.14×12×+(8÷2)2×3.14×12
=16×3.14×4+16×3.14×12
=200.96+602.88
=803.84(cm3)
【分析】(1)已知圆锥的底面直径和高,要求圆锥的体积,V=π(d÷2)2h;
(2)观察图可知,这个组合图形的体积=圆锥的体积+圆柱的体积,V=π(d÷2)2h+π(d÷2)2h。
23.【答案】解:侧面积=94.2×20=1884(平方厘米)
答:这个石墩的侧面积是1884平方厘米。
【分析】圆柱的侧面积=圆柱的底面周长×圆柱的高,代入数值计算即可得出答案。
24.【答案】解:由题意知烟囱的底面周长是31.4cm,所以底面直径是31.4÷3.14=10(cm).
答:这节烟囱的底面直径是10厘米.
【分析】由于长边是烟囱的高,那么31.4cm就是烟囱的底面周长,用底面周长除以3.14即可求出底面直径.
25.【答案】解:
答:涂褐色部分的面积是175.84平方厘米.
【分析】用底面周长乘高求出这个笔筒的侧面积,用侧面积乘即可求出涂褐色部分的面积.
26.【答案】解:40÷2÷10
=20÷10
= 2(dm)
3.14×22×10
=12.56×10
=125.6(dm3)
答:原来圆柱的体积是125.6立方分米。
【分析】把圆柱切拼成一个近似的长方体,表面积增加了2个长方形的面积,所以圆柱的底面半径=增加的表面积÷2÷圆柱的高,所以原来圆柱的体积=πr2h,据此代入数值作答即可。
27.【答案】解:31.4÷3.14÷2=5(米)
3.14×52×3÷3
=3.14×25×3÷3
=78.5(立方米)
2厘米=0.02米
78.5÷10÷0.02
=7.85÷2
=392.5(米)
答: 这些沙子能铺392.5米的路。
【分析】先根据圆锥的底面周长求出它的底面半径,从而利用圆锥的体积公式求出这堆沙的体积,再利用长方体的体积公式即可求出沙子的长度。
21世纪教育网(www.21cnjy.com)
第一单元 圆柱和圆锥单元常考易错卷(基础卷)
北师大版数学 六年级下册
一、填空题
1.圆柱上下面是两个 的圆形,有 个面是弯曲的;圆锥的底面是一个 形,侧面是一个 面。
2.把圆柱的 展开可以得到一个长方形,这个长方形的长等于圆柱的 ,宽等于圆柱的 。
3. 一个底面半径3cm,高7cm的圆柱的侧面沿高剪开得到一个长方形,这个长方形的长是 cm,宽是 cm。
4.把一张边长是40厘米的正方形纸片,卷成一个最大的圆柱形纸筒。它的底面周长是 厘米,高是 厘米。
5.如图是一个圆柱的表面展开图,这个圆柱的侧面积是 cm2,表面积是 cm2。
6.一个圆锥的体积是81立方厘米,底面积是27平方厘米,它的高是 厘米。
7.一个圆柱和一个圆锥等底等高,圆锥的体积是38.4立方厘米,圆柱的体积比圆锥的体积多 立方厘米。
8.圆柱的底面半径扩大3倍,高不变,它的侧面积扩大 倍,它的体积扩大 倍,它的底面积扩大 倍。
9.一段体积是52.8立方厘米的圆柱形木料,切削成一个最大的圆锥,削去部分的体积是 立方厘米。
10.一个圆锥形容器盛满水,水深为18厘米,将圆锥形容器的水倒入和它等底等高的圆柱形容器中,水深为 厘米。
二、单选题
11.在下图中,以直线为旋转轴 ,可以得到圆柱的是( )。
A. B. C. D.
12.把一个圆锥沿底面直径到顶点切开,切面是一个( )。
A.圆形 B.三角形 C.扇形 D.无法确定
13.把一个圆柱形罐头盒的侧面打开,得到一个正方形。这个圆柱形罐头盒的底面半径是10cm,高是( )cm。
A.20 B.31.4 C.62.8 D.3140
14.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱的3倍,圆锥的体积是12立方分米,圆柱的体积是()立方分米。
A.12 B.36 C.4 D.8
15.如图,长方形的长是 4 cm,宽是 2 cm,分别以长边和宽边所在的直线为轴,旋转一周可以得到两个不同的圆柱。这两个圆柱的体积相比较,( )。
A.甲大 B.乙大 C.同样大 D.无法判断
三、判断题
16.圆柱的上、下底面都是圆,且大小一样。( )
17.从圆锥的顶点到底面圆周上任意一点的距离是圆锥的高。( )
18.长方体、正方体、圆柱和圆锥的体积都可以用“底面积×高”计算。
19.圆锥的体积等于圆柱体积的 。( )
20.如果两个圆柱的侧面积相等,那么它们的底面周长也一定相等。( )
四、计算题
21.计算圆柱的表面积。(单位:厘米)
22.求下面图形的体积。(单位:cm)
(1)
(2)
五、解决问题
23.一个圆柱形石墩,底面周长是94.2cm,高是20cm。这个石墩的侧面积是多少平方厘米?
24.工人李师傅用一块长90cm、宽31.4cm的铁皮焊接一节长90cm的圆柱体烟囱,这节烟囱的底面直径是多少
25.如图,冬冬要把自己做的圆柱形笔筒的 高度以下涂上褐色(底面不涂),涂褐色部分的面积是多少平方厘米?
26.如下图,把一个高是10dm的圆柱切拼成一个近似的长方体,已知拼成的长方体的表面积比原来圆柱的表面积增加了40dm2,则原来圆柱的体积是多少立方分米?
27.在建筑工地上有一个近似于圆锥形状的沙堆,测得其底面周长是31.4m,高是3m。把这些沙子铺在宽10m的路上,平均厚度为2cm,这些沙子能铺多长的路
答案解析部分
1.【答案】相同;1;圆;扇形
【解答】解:圆柱的上下面是两个相同的圆形,有1个面是弯曲的;圆锥的底面是一个圆形,侧面是一个扇形。
故答案为:相同;1;圆;扇形。
【分析】圆柱是上下两个面是相同的圆形,圆柱的侧面是一个曲面,沿着一条高展开后是一个长方形;圆锥的底面是一个圆形,侧面展开后是一个扇形。
2.【答案】侧面;底面周长(高);高(底面周长)
【解答】解:把圆柱的侧面展开可以得到一个长方形,这个长方形的长等于圆柱的底面周长(高),宽等于圆柱的高(底面周长)。
故答案为:侧面; 底面周长(高); 高(底面周长)。
【分析】圆柱的侧面沿高展开是一个长方形,长方形的长相当于圆柱底面周长,宽相当于圆柱的高;当底面周长和高相等时,就得到一个正方形,正方形的边长相当于圆柱的底面周长和高;斜着剪开得到一个平行四边形,平行四边形的底相当于圆柱底面周长,高相当于圆柱的高。
3.【答案】18.84;7
【解答】解:长:3.14×2×3
=6.28×3
=18.84(cm);
宽是7厘米;
故答案为:18.84;7。
【分析】展开得到的长方形的长就是圆柱的底面周长,底面周长=π×2×半径,宽就是圆柱的高,据此解答。
4.【答案】40;40
【解答】正方形卷成最大的圆柱可知,圆柱的底面周长和圆柱的高都等于正方形的边长,正方形的边长=40厘米,则圆柱的底面周长和圆柱的高也是都是40厘米。
故答案为:40;40。
【分析】根据圆柱的侧面展开图,卷成的圆柱的侧面展开是一个正方形,则正方形的一条边长是圆柱的底面周长,另一条相邻的边长是圆柱的高,题目已经告知正方形的边长,则圆柱的底面周长和圆柱的高就可以得出。
5.【答案】251.2;351.68
【解答】解:25.12×10=251.2(平方厘米)
25.12÷3.14÷2=4(厘米)
3.14×4×4=50.24(平方厘米)
50.24×2+251.2=100.48+251.2=351.68(平方厘米)
故答案为:251.2;351.68。
【分析】底面周长×高=侧面积;底面周长÷π÷2=底面半径,π×底面半径的平方=底面积;圆柱的底面积×2+圆柱的侧面积=圆柱的表面积。
6.【答案】9
【解答】81×3÷27
=243÷27
=9(厘米)
故答案为:9.
【分析】根据圆锥的体积公式:V=Sh,已知圆锥的体积和底面积,求圆锥的高,用圆锥的体积×3÷圆锥的底面积=圆锥的高,据此列式解答.
7.【答案】76.8
【解答】38.4×(3-1)
=38.4×2
=76.8(立方厘米)
故答案为:76.8。
【分析】 一个圆柱和一个圆锥等底等高,圆柱的体积是圆锥体积的3倍,圆柱的体积比圆锥体积多圆锥体积的(3-1)倍,据此列式解答.
8.【答案】3;9;9
【解答】解:圆柱的底面半径扩大3倍,高不变,它的侧面积扩大3倍,它的体积扩大9倍,它的底面积扩大9倍。
故答案为:3;9;9。
【分析】圆柱的高不变,底面半径扩大几倍,相应地,侧面积就扩大几倍,体积扩大几2倍,底面积扩大几2倍。
9.【答案】35.2
【解答】将圆柱形木料切削成一个最大的圆锥,这个圆锥是与它等底等高的圆锥,此时圆锥的体积=圆柱的体积×,所以削去部分的体积为52.8-52.8×=35.2(立方厘米)。
故答案为:35.2.
【分析】圆柱形木料切削成一个最大的圆锥,这个圆锥是与它等底等高的圆锥,圆锥的体积=圆柱的体积×。
10.【答案】6
【解答】当圆柱和圆锥的底面积和体积相等时,高之比为1:3,则在该题中,圆柱中水的高度为6厘米。
故答案为:6.
【分析】根据等底等高的圆柱体积是圆锥体积的3倍可知,体积和底面积相等的圆柱和圆锥,圆柱的高是圆锥高的,据此解答.
11.【答案】A
【解答】在下图中,以直线为旋转轴,可以得到圆柱的是.
故答案为:A.
【分析】根据对圆柱特征的理解可知,一个长方形以长或宽为旋转轴,旋转一周形成的图形是圆柱体,据此解答.
12.【答案】B
【解答】解:把一个圆锥沿底面直径到顶点切开,切面是一个三角形.
故答案为:B
【分析】圆锥是一个圆形的底面和一个曲面组成的,曲面展开后是一个扇形,根据圆锥的特征可知把一个圆锥沿底面直径到顶点切开,切面是一个三角形.
13.【答案】C
【解答】解:3.14×10×2=62.8(cm)。
故答案为:C。
【分析】圆柱的底面周长和高相等时,圆柱的侧面展开后才是正方形。根据圆周长公式计算出底面周长,也就是高。
14.【答案】A
解答:由题意,底面直径相等,所以半径也相等,设圆柱和圆锥的体积分别是 , ,圆锥的体积是12立方分米,所以圆柱的体积也是12立方分米。
分析:由圆柱的体积和圆锥的体积公式。
15.【答案】B
【解答】解:甲形成的圆柱,底面半径是2厘米,高是4厘米,
体积:π×2×2×4=16π,
乙形成的圆柱,底面半径是4厘米,高是2厘米,
体积:π×4×4×2=32π,
这两个圆柱的体积相比较,乙大 。
故答案为:B。
【分析】π×底面半径的平方×高=圆柱的体积;据此先计算,再比较。
16.【答案】正确
【解答】解:圆柱的上、下底面都是圆,且大小一样。原题说法正确。
故答案为:正确。
【分析】圆柱的上、下两个面是完全相同的两个圆形。
17.【答案】错误
【解答】解:从圆锥的顶点到底面圆心的距离是圆锥的高。原题说法错误。
故答案为:错误。
【分析】圆锥只有一条高,是圆锥顶点到底面圆心的距离。
18.【答案】错误
【解答】解:长方体、正方体、圆柱可以用“底面积×高”计算,圆锥的体积=底面积×高×。原题说法错误。
故答案为:错误。
【分析】长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,长×宽是长方体的底面积,棱长×棱长是正方体的底面积;圆柱的体积=底面积×高,圆锥的体积=底面积×高×。
19.【答案】错误
【解答】解:圆锥的体积等于与之等底等高的圆柱体积的。
故答案为:错误。
【分析】圆锥的体积等于与之等底等高的圆柱体积的
20.【答案】错误
【解答】根据分析得:圆柱的侧面积与底面周长、高两个条件相关。
所以 如果两个圆柱的侧面积相等,那么它们的底面周长不一定相等。
故答案为:错误。
【分析】 因为圆柱的侧面积=底面周长×高,若两个圆柱的侧面积相等,但底面周长和高不一定相等,所以它们的底面周长不一定相等。据此判断。
21.【答案】解:2÷2=1(厘米)
3.14×12×2+3.14×2×0.8
=6.28+5.024
=11.304(厘米)
【分析】圆柱的表面积=底面积×2+侧面积;侧面积=底面周长×高。
22.【答案】(1)(6÷2)2×3.14×6×
=9×3.14×2
=28.26×2
=56.52(cm3)
(2)(8÷2)2×3.14×12×+(8÷2)2×3.14×12
=16×3.14×4+16×3.14×12
=200.96+602.88
=803.84(cm3)
【分析】(1)已知圆锥的底面直径和高,要求圆锥的体积,V=π(d÷2)2h;
(2)观察图可知,这个组合图形的体积=圆锥的体积+圆柱的体积,V=π(d÷2)2h+π(d÷2)2h。
23.【答案】解:侧面积=94.2×20=1884(平方厘米)
答:这个石墩的侧面积是1884平方厘米。
【分析】圆柱的侧面积=圆柱的底面周长×圆柱的高,代入数值计算即可得出答案。
24.【答案】解:由题意知烟囱的底面周长是31.4cm,所以底面直径是31.4÷3.14=10(cm).
答:这节烟囱的底面直径是10厘米.
【分析】由于长边是烟囱的高,那么31.4cm就是烟囱的底面周长,用底面周长除以3.14即可求出底面直径.
25.【答案】解:
答:涂褐色部分的面积是175.84平方厘米.
【分析】用底面周长乘高求出这个笔筒的侧面积,用侧面积乘即可求出涂褐色部分的面积.
26.【答案】解:40÷2÷10
=20÷10
= 2(dm)
3.14×22×10
=12.56×10
=125.6(dm3)
答:原来圆柱的体积是125.6立方分米。
【分析】把圆柱切拼成一个近似的长方体,表面积增加了2个长方形的面积,所以圆柱的底面半径=增加的表面积÷2÷圆柱的高,所以原来圆柱的体积=πr2h,据此代入数值作答即可。
27.【答案】解:31.4÷3.14÷2=5(米)
3.14×52×3÷3
=3.14×25×3÷3
=78.5(立方米)
2厘米=0.02米
78.5÷10÷0.02
=7.85÷2
=392.5(米)
答: 这些沙子能铺392.5米的路。
【分析】先根据圆锥的底面周长求出它的底面半径,从而利用圆锥的体积公式求出这堆沙的体积,再利用长方体的体积公式即可求出沙子的长度。
21世纪教育网(www.21cnjy.com)
