湖北省北大附中武汉为明实验学校人教版七年级数学下册导学案:7.1有序数对(表格式无答案)
文档属性
| 名称 | 湖北省北大附中武汉为明实验学校人教版七年级数学下册导学案:7.1有序数对(表格式无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 93.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-05 00:00:00 | ||
图片预览


文档简介
课题:7.1.1 有序数对
编制人:金丽敏
审核人:
执教老师:
授课日期:
学生姓名:
学习
目标
1.会用有序数对表示物体的位置。
2.结合用有序数对表示物体的位置内容,体会数形结合的思想。
学习重点
理解有序数对的概念,用有序数对来表示位置。
学习难点
理解有序数对是“有序的”并用它解决实际问题
学习过程
教师二次备课
或学生笔记
一、自主学习 了解新知(独学)
任务1:游戏:“找自己班级的同学”.
问题:(1)只给一个数据如“第3列”,你能确定该同学的位置吗?
(2)给两个数据如“第3列第2排”,你确定的同“第3列”是一个位置吗?为什么?
任务2:你能用自己的语言说出自己所在班级里的位置吗?
(1)如何找到4列3排这个座位呢?(先找什么,后找什么)
(2)在班级“4列3排”与“3列4排”有什么不同?坐的是一个同学吗?
(3)如果将“4列3排”简记作(4,3),那么“3排4座”如何表示?
(4)(2,3)表示什么含义?(3,2)呢?观察上述问题,从中能够得出什么结论?
想一想:在班级里,确定一个座位一般需要几个数据,为什么?
二、合作探究 掌握新知(对学、群学、展示)
任务1:问题1: 如果我们约定:“列数”在前,“排数”在后,
A(1,3)
(1)请在下面教室平面图中找到以下用数对表示的位置,将数对填入相应
A(1,3),B(3,1),C(4,6),D(6,4), E(2,5), F(5,2), G(3,3), H(5,6).
(2)在上面的表示里,(1,3)和(3,1)它们表示的位置相同吗?为什么?答: 。
(3)课本中的“约定”是了什么?答: 。
归纳: 的两个数a与b组成的数对,叫做有序数对.记作 。
问题2 请你再举出一个用有序数对表示位置的例子,并数学符号表示出来:答: 。
例如下列座位表中(1,3)表示A在第一列第三排,
点拨:1.应用以上方法确定位置时,应事先规定,规定列数写在前,排数写在后。
2.有序数对中的每个数代表不同的含义,解决这类问题,需要弄清数对中每个数所代表的含义,数的顺序不能颠倒。
三、知识应用 巩固新知(小组合作,学能展示)
任务1:基础知识
1. 的两个数a与b组成的数对,叫做有序数对.记作 。
立
明
数
学
校
做
我
们
上
二
名
不
七
中
一
爱
国
为
是
志
个
好
人
民
工
作
秀
序
对
生
年
优
有
复
习
活
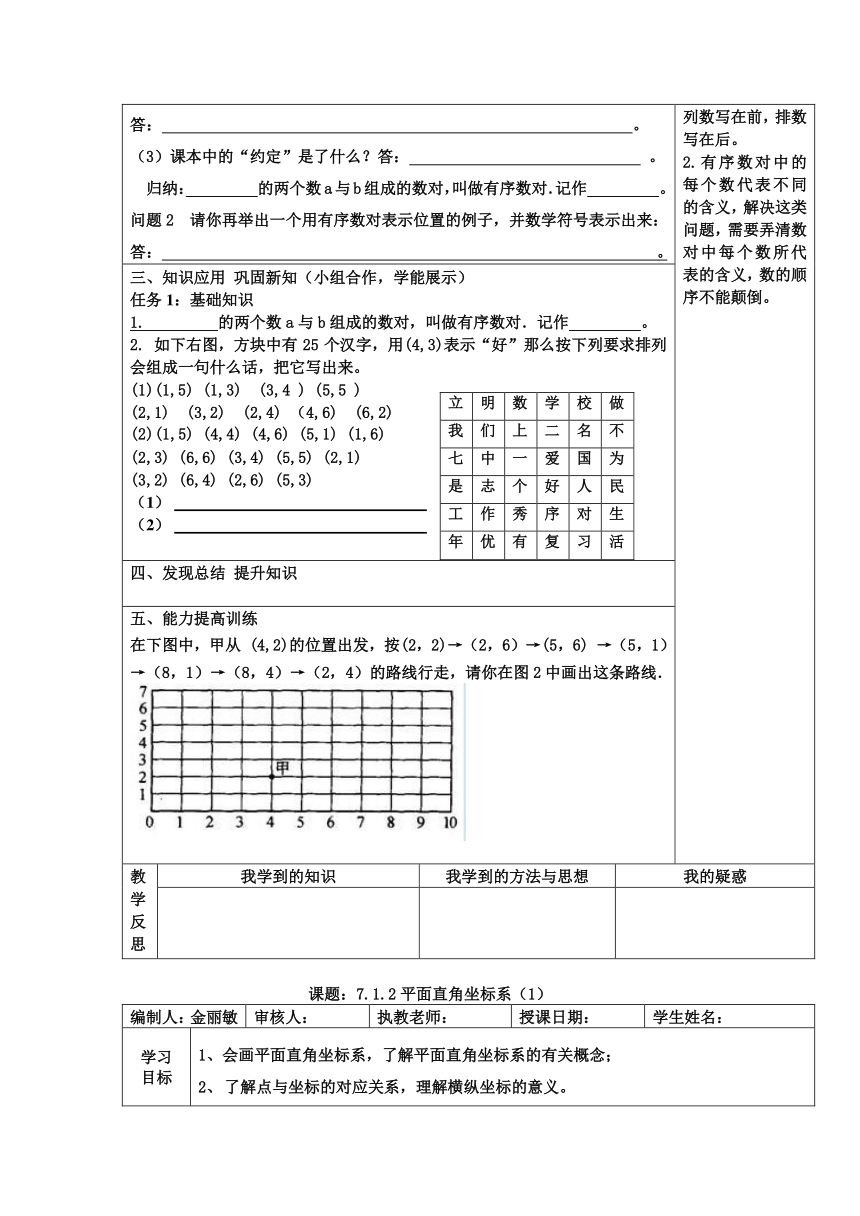
2. 如下右图,方块中有25个汉字,用(4,3)表示“好”那么按下列要求排列会组成一句什么话,把它写出来。
(1)(1,5) (1,3) (3,4 ) (5,5 )
(2,1) (3,2) (2,4) (4,6) (6,2)
(1,5) (4,4) (4,6) (5,1) (1,6)
(2,3) (6,6) (3,4) (5,5) (2,1)
(3,2) (6,4) (2,6) (5,3)
四、发现总结 提升知识
五、能力提高训练
在下图中,甲从 (4,2)的位置出发,按(2,2)→(2,6)→(5,6) →(5,1)→(8,1)→(8,4)→(2,4)的路线行走,请你在图2中画出这条路线.
教学反思
我学到的知识
我学到的方法与思想
我的疑惑
课题:7.1.2平面直角坐标系(1)
编制人:金丽敏
审核人:
执教老师:
授课日期:
学生姓名:
学习
目标
1、会画平面直角坐标系,了解平面直角坐标系的有关概念;
了解点与坐标的对应关系,理解横纵坐标的意义。
学习重点
根据点的坐标在直角坐标系中描出点的位置。
学习难点
探索特殊的点与坐标之间的关系
学习过程
教师二次备课或学生笔记
一、自主学习 了解新知(独学)
任务1: ①规定了 、 、 的直线叫做数轴。
②数轴上原点及原点右边的点表示的数是 ;原点左边的点表示的数是 。
③画数轴时,一般规定向 (或向 )为正方向。
任务2:指出数轴上A、B、C、D、E各点分别表示什么数:
A点表示______,B点表示______,C点表示______,D点表示_____。
2、思考:能不能有一种办法来确定平面内的点的位置呢?
二、合作探究 掌握新知(对学、群学、展示)
任务1:平面直角坐标系概念:
1.平面内画两条互相 、原点 的数轴,组成平面直角坐标系.
2.水平的数轴称为 或 ,习惯上取向 为正方向;竖直的数轴为 或 ,取向 为正方向;两个坐标轴的交点为平面直角坐标系的 。
任务2:点的坐标:
我们用一个 表示平面上的点,这对数叫 。
表示方法为(a , b). a是点对应 上的数值,b是点在 上对应的数值。如右图,由点A向x轴作 ,垂足在 上的坐标是 ,我们说点A的横坐标是 ; 由点A向y轴做 ,垂足在 上的坐标是 ,我们说点A的 是 ;则,这样我们就可以利用有序数对 来表示点A的位置,且这组有序数对 叫做点A的坐标;
记作 ;
【练一练】仿照确定点A坐标的方法,写出下列各点的坐标:
A ;B ;C ;
D ;E ;F ;
G ;H ;M ;
N ;O ;
任务2:象限:
建立平面直角坐标系后,平面被坐标轴分成 部分,
分别叫第一象限,第二象限,第三象限和第四象限。
第二象限(—,+) 第一象限(+,+)
第三象限(—,—) 第四象限(+,—)
2、注意:坐标轴上的点不属于任何一个象限
3、你能说出上面例子中各点在第几象限吗?
任务3:你是怎样理解“坐标平面内的点与有序实数对是一一对应的”?
三、知识应用 巩固新知(小组合作,学能展示)
任务1:基础知识
在直角坐标系中描出下列各点,并指出它们分别在什么位置?
A(-4,-2)、B(2,-3)、C(4,3)、D(-5,2)、E(0,-4)、F(-2,0)、G(0,0)
2、三角形中,A、B、C三点的坐标分别为A(0,3),B(4,3),C(1,-1),在平面直角坐标系内描出各点,并求三角形ABC的面积。
任务2:拓展提升
若第一象限内的点A到x轴的距离是4,到y轴的距离是7,则点A( , )
点B到x轴的距离是3,到y轴的距离是5,则点B的坐标是
。
四、发现总结 提升知识
教学反思
我学到的知识
我学到的方法与思想
我的疑惑
7.1.2 平面直角坐标系(2)
学习目标: 1、能识别平面直角坐标系中的特殊点,并利用它们的特征解决问题。
2、让学生经历、体验特殊点的坐标的特点的过程,进一步体会数形结合思想。
3、培养自主、合作的学习方法,提高学习数学的积极性。
学习重点:各象限内的点的坐标的特征。
学习难点:特殊点的识别与应用。
学习过程:
一、自主学习
如图,填空:(写出各点坐标并说明横、纵坐标)
(1)A(____,___)横坐标:_____,纵坐标:_____;
(2)B(____,___)横坐标:_____,纵坐标:_____;
(3)C(____,___)横坐标:_____,纵坐标:_____;
(4)D(____,___)横坐标:_____,纵坐标:_____;
(5)E(____,___)横坐标:_____,纵坐标:_____;
(6)F(____,___)横坐标:_____,纵坐标:_____;
(7)G(____,___)横坐标:_____,纵坐标:_____;
(8)H(____,___)横坐标:_____,纵坐标:_____;
(9)I(____,___)横坐标:_____,纵坐标:_____.
(10)J(____,___)横坐标:____,纵坐标:_____
二、探究新知
坐标轴上的点的坐标的特点:
x轴上的点的 坐标为0,y轴上的点的 坐标为0.
x轴的正半轴的横坐标是 数,纵坐标为 ,x轴的负半轴的横坐标是 数,纵坐标为 ;
y轴的正半轴的纵坐标是 数,横坐标为 ,y轴的负半轴的纵坐标是 数,横坐标为 ;
坐标原点的坐标为 .
象限及各象限内的点的坐标的特点:
建立直角坐标系以后,坐标平面就被两条坐标轴
把这个平面分成了__个部分,分别叫做第 象限、
第 象限、第 象限和第 象限。
第一象限内的点的横坐标为 ,纵坐标为 ;
第二象限内的点的横坐标为 ,纵坐标为 ;
第三象限内的点的横坐标为 ,纵坐标为 ;
第四象限内的点的横坐标为 ,纵坐标为 。
指出上题中A、B、C、D、E、F、G、H、I、J各点,点 在第一象限内,点____在第二象限内,点_____在第三象限内,点____在第四象限内;点 在x轴上,点 在y轴上.
平行于坐标轴的两个点的坐标的特点:
平行于x轴的两个点的 坐标 ;平行于y轴的两个点的 坐标 .
各象限内的角平分线上的点的坐标的特点:
1、若点P(a,b)在第一、三象限的角平分线上,则a,b满足关系 : ;
2、若点P(a,b)在第二、四象限的角平分线上,则a,b满足关系: 。
点到两坐标轴的距离:点P(a,b)到x轴的距离为 , 点P(a,b)到y轴的距离为 .
三、应用新知
1、分别写出位于一、二、三、四象限内各一个点: , , , 。
2、分别写出位于x轴、y轴上各两点: , , , 。
3、分别写出位于各象限内角平分线上各一点: , , , 。
4、若点A(a -9,a+2)在y轴上,则a=______;点P(m+3, m+1)在x轴上,则点P为 。
5、点A(2,-3)在第_____象限;点B(-2,3)在第_____象限;点C(2,3)在第_____象限;
点D(-2,-3)在第_____象限;点E(0,3)在 上;点F(-4,0)在 上。
四、总结发现
坐标平面内的点的坐标有如下特征:
若点P(x,y)在第一象限,则x>0,y>0. 若点P(x,y)在第二象限,则 .
若点P(x,y)在第三象限,则 . 若点P(x,y)在第四象限,则 .
若点P(x,y)在x轴上,则 . 若点P(x,y)在y轴上,则 .若点P(x,y)在原点,则 . 点P(x,y) 到x轴的距离为 , 点P(x,y) 到y轴的距离为 .
已知:点A(x1,y1),B(x2,y2),若AB∥x轴,则 ,若AB∥y轴,则 .
课堂检测
1、点A(-3,2)在第_____象限,点B(-3,-2)在第______象限,点C( 3, 2) 在第_____象限,点D(3,-2)在第_____象限,点E(0,2)在_____轴上, 点F(2,0) 在_____轴上
2、如果点P(a+5,a-2)在x轴上,那么P点坐标为________.
3、点A(-2,-5)与x轴的距离是________;与y轴的距离是________.
4、点M(a,b)在第二象限,则点N(b,b-a)在________象限.
5、点A(3,a)在x轴上,点B(b,4)在y轴上,则a=______,b=______,S△AOB=_____.
6、已知A(6,0),B(2,1),C(0,0),则三角形ABC的面积为 。
7、已知点M(4a-8,a+3),分别根据下列条件求出点M的坐标:
(1)点M在y轴上; (2)点N的坐标为(3,-6),并且直线MN∥x轴。
教学反思:
我学到的知识
我学到的方法和思想
我的疑惑
编制人:金丽敏
审核人:
执教老师:
授课日期:
学生姓名:
学习
目标
1.会用有序数对表示物体的位置。
2.结合用有序数对表示物体的位置内容,体会数形结合的思想。
学习重点
理解有序数对的概念,用有序数对来表示位置。
学习难点
理解有序数对是“有序的”并用它解决实际问题
学习过程
教师二次备课
或学生笔记
一、自主学习 了解新知(独学)
任务1:游戏:“找自己班级的同学”.
问题:(1)只给一个数据如“第3列”,你能确定该同学的位置吗?
(2)给两个数据如“第3列第2排”,你确定的同“第3列”是一个位置吗?为什么?
任务2:你能用自己的语言说出自己所在班级里的位置吗?
(1)如何找到4列3排这个座位呢?(先找什么,后找什么)
(2)在班级“4列3排”与“3列4排”有什么不同?坐的是一个同学吗?
(3)如果将“4列3排”简记作(4,3),那么“3排4座”如何表示?
(4)(2,3)表示什么含义?(3,2)呢?观察上述问题,从中能够得出什么结论?
想一想:在班级里,确定一个座位一般需要几个数据,为什么?
二、合作探究 掌握新知(对学、群学、展示)
任务1:问题1: 如果我们约定:“列数”在前,“排数”在后,
A(1,3)
(1)请在下面教室平面图中找到以下用数对表示的位置,将数对填入相应
A(1,3),B(3,1),C(4,6),D(6,4), E(2,5), F(5,2), G(3,3), H(5,6).
(2)在上面的表示里,(1,3)和(3,1)它们表示的位置相同吗?为什么?答: 。
(3)课本中的“约定”是了什么?答: 。
归纳: 的两个数a与b组成的数对,叫做有序数对.记作 。
问题2 请你再举出一个用有序数对表示位置的例子,并数学符号表示出来:答: 。
例如下列座位表中(1,3)表示A在第一列第三排,
点拨:1.应用以上方法确定位置时,应事先规定,规定列数写在前,排数写在后。
2.有序数对中的每个数代表不同的含义,解决这类问题,需要弄清数对中每个数所代表的含义,数的顺序不能颠倒。
三、知识应用 巩固新知(小组合作,学能展示)
任务1:基础知识
1. 的两个数a与b组成的数对,叫做有序数对.记作 。
立
明
数
学
校
做
我
们
上
二
名
不
七
中
一
爱
国
为
是
志
个
好
人
民
工
作
秀
序
对
生
年
优
有
复
习
活
2. 如下右图,方块中有25个汉字,用(4,3)表示“好”那么按下列要求排列会组成一句什么话,把它写出来。
(1)(1,5) (1,3) (3,4 ) (5,5 )
(2,1) (3,2) (2,4) (4,6) (6,2)
(1,5) (4,4) (4,6) (5,1) (1,6)
(2,3) (6,6) (3,4) (5,5) (2,1)
(3,2) (6,4) (2,6) (5,3)
四、发现总结 提升知识
五、能力提高训练
在下图中,甲从 (4,2)的位置出发,按(2,2)→(2,6)→(5,6) →(5,1)→(8,1)→(8,4)→(2,4)的路线行走,请你在图2中画出这条路线.
教学反思
我学到的知识
我学到的方法与思想
我的疑惑
课题:7.1.2平面直角坐标系(1)
编制人:金丽敏
审核人:
执教老师:
授课日期:
学生姓名:
学习
目标
1、会画平面直角坐标系,了解平面直角坐标系的有关概念;
了解点与坐标的对应关系,理解横纵坐标的意义。
学习重点
根据点的坐标在直角坐标系中描出点的位置。
学习难点
探索特殊的点与坐标之间的关系
学习过程
教师二次备课或学生笔记
一、自主学习 了解新知(独学)
任务1: ①规定了 、 、 的直线叫做数轴。
②数轴上原点及原点右边的点表示的数是 ;原点左边的点表示的数是 。
③画数轴时,一般规定向 (或向 )为正方向。
任务2:指出数轴上A、B、C、D、E各点分别表示什么数:
A点表示______,B点表示______,C点表示______,D点表示_____。
2、思考:能不能有一种办法来确定平面内的点的位置呢?
二、合作探究 掌握新知(对学、群学、展示)
任务1:平面直角坐标系概念:
1.平面内画两条互相 、原点 的数轴,组成平面直角坐标系.
2.水平的数轴称为 或 ,习惯上取向 为正方向;竖直的数轴为 或 ,取向 为正方向;两个坐标轴的交点为平面直角坐标系的 。
任务2:点的坐标:
我们用一个 表示平面上的点,这对数叫 。
表示方法为(a , b). a是点对应 上的数值,b是点在 上对应的数值。如右图,由点A向x轴作 ,垂足在 上的坐标是 ,我们说点A的横坐标是 ; 由点A向y轴做 ,垂足在 上的坐标是 ,我们说点A的 是 ;则,这样我们就可以利用有序数对 来表示点A的位置,且这组有序数对 叫做点A的坐标;
记作 ;
【练一练】仿照确定点A坐标的方法,写出下列各点的坐标:
A ;B ;C ;
D ;E ;F ;
G ;H ;M ;
N ;O ;
任务2:象限:
建立平面直角坐标系后,平面被坐标轴分成 部分,
分别叫第一象限,第二象限,第三象限和第四象限。
第二象限(—,+) 第一象限(+,+)
第三象限(—,—) 第四象限(+,—)
2、注意:坐标轴上的点不属于任何一个象限
3、你能说出上面例子中各点在第几象限吗?
任务3:你是怎样理解“坐标平面内的点与有序实数对是一一对应的”?
三、知识应用 巩固新知(小组合作,学能展示)
任务1:基础知识
在直角坐标系中描出下列各点,并指出它们分别在什么位置?
A(-4,-2)、B(2,-3)、C(4,3)、D(-5,2)、E(0,-4)、F(-2,0)、G(0,0)
2、三角形中,A、B、C三点的坐标分别为A(0,3),B(4,3),C(1,-1),在平面直角坐标系内描出各点,并求三角形ABC的面积。
任务2:拓展提升
若第一象限内的点A到x轴的距离是4,到y轴的距离是7,则点A( , )
点B到x轴的距离是3,到y轴的距离是5,则点B的坐标是
。
四、发现总结 提升知识
教学反思
我学到的知识
我学到的方法与思想
我的疑惑
7.1.2 平面直角坐标系(2)
学习目标: 1、能识别平面直角坐标系中的特殊点,并利用它们的特征解决问题。
2、让学生经历、体验特殊点的坐标的特点的过程,进一步体会数形结合思想。
3、培养自主、合作的学习方法,提高学习数学的积极性。
学习重点:各象限内的点的坐标的特征。
学习难点:特殊点的识别与应用。
学习过程:
一、自主学习
如图,填空:(写出各点坐标并说明横、纵坐标)
(1)A(____,___)横坐标:_____,纵坐标:_____;
(2)B(____,___)横坐标:_____,纵坐标:_____;
(3)C(____,___)横坐标:_____,纵坐标:_____;
(4)D(____,___)横坐标:_____,纵坐标:_____;
(5)E(____,___)横坐标:_____,纵坐标:_____;
(6)F(____,___)横坐标:_____,纵坐标:_____;
(7)G(____,___)横坐标:_____,纵坐标:_____;
(8)H(____,___)横坐标:_____,纵坐标:_____;
(9)I(____,___)横坐标:_____,纵坐标:_____.
(10)J(____,___)横坐标:____,纵坐标:_____
二、探究新知
坐标轴上的点的坐标的特点:
x轴上的点的 坐标为0,y轴上的点的 坐标为0.
x轴的正半轴的横坐标是 数,纵坐标为 ,x轴的负半轴的横坐标是 数,纵坐标为 ;
y轴的正半轴的纵坐标是 数,横坐标为 ,y轴的负半轴的纵坐标是 数,横坐标为 ;
坐标原点的坐标为 .
象限及各象限内的点的坐标的特点:
建立直角坐标系以后,坐标平面就被两条坐标轴
把这个平面分成了__个部分,分别叫做第 象限、
第 象限、第 象限和第 象限。
第一象限内的点的横坐标为 ,纵坐标为 ;
第二象限内的点的横坐标为 ,纵坐标为 ;
第三象限内的点的横坐标为 ,纵坐标为 ;
第四象限内的点的横坐标为 ,纵坐标为 。
指出上题中A、B、C、D、E、F、G、H、I、J各点,点 在第一象限内,点____在第二象限内,点_____在第三象限内,点____在第四象限内;点 在x轴上,点 在y轴上.
平行于坐标轴的两个点的坐标的特点:
平行于x轴的两个点的 坐标 ;平行于y轴的两个点的 坐标 .
各象限内的角平分线上的点的坐标的特点:
1、若点P(a,b)在第一、三象限的角平分线上,则a,b满足关系 : ;
2、若点P(a,b)在第二、四象限的角平分线上,则a,b满足关系: 。
点到两坐标轴的距离:点P(a,b)到x轴的距离为 , 点P(a,b)到y轴的距离为 .
三、应用新知
1、分别写出位于一、二、三、四象限内各一个点: , , , 。
2、分别写出位于x轴、y轴上各两点: , , , 。
3、分别写出位于各象限内角平分线上各一点: , , , 。
4、若点A(a -9,a+2)在y轴上,则a=______;点P(m+3, m+1)在x轴上,则点P为 。
5、点A(2,-3)在第_____象限;点B(-2,3)在第_____象限;点C(2,3)在第_____象限;
点D(-2,-3)在第_____象限;点E(0,3)在 上;点F(-4,0)在 上。
四、总结发现
坐标平面内的点的坐标有如下特征:
若点P(x,y)在第一象限,则x>0,y>0. 若点P(x,y)在第二象限,则 .
若点P(x,y)在第三象限,则 . 若点P(x,y)在第四象限,则 .
若点P(x,y)在x轴上,则 . 若点P(x,y)在y轴上,则 .若点P(x,y)在原点,则 . 点P(x,y) 到x轴的距离为 , 点P(x,y) 到y轴的距离为 .
已知:点A(x1,y1),B(x2,y2),若AB∥x轴,则 ,若AB∥y轴,则 .
课堂检测
1、点A(-3,2)在第_____象限,点B(-3,-2)在第______象限,点C( 3, 2) 在第_____象限,点D(3,-2)在第_____象限,点E(0,2)在_____轴上, 点F(2,0) 在_____轴上
2、如果点P(a+5,a-2)在x轴上,那么P点坐标为________.
3、点A(-2,-5)与x轴的距离是________;与y轴的距离是________.
4、点M(a,b)在第二象限,则点N(b,b-a)在________象限.
5、点A(3,a)在x轴上,点B(b,4)在y轴上,则a=______,b=______,S△AOB=_____.
6、已知A(6,0),B(2,1),C(0,0),则三角形ABC的面积为 。
7、已知点M(4a-8,a+3),分别根据下列条件求出点M的坐标:
(1)点M在y轴上; (2)点N的坐标为(3,-6),并且直线MN∥x轴。
教学反思:
我学到的知识
我学到的方法和思想
我的疑惑
