2024-2025学年北师大版九年级数学下册 1.1 锐角三角函数(1) 正切 课件(共28张PPT)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学下册 1.1 锐角三角函数(1) 正切 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 00:00:00 | ||
图片预览




文档简介
(共28张PPT)
北师大版九年级数学下册课件
第一章 直角三角形的边角关系
1 锐角三角函数
课时1 正切
1.理解正切的意义和与现实生活的联系.
2.能够用 表示直角三角形中两直角边的比,表示生活中
物体的倾斜程度、坡度(坡比)等.(重点)
3.能够根据直角三角形的边角关系,用正切进行简单的计
算.(难点)
学习目标
新课导入
生活中的梯子
梯子是我们日常生活中常见的物体.
新课导入
思考
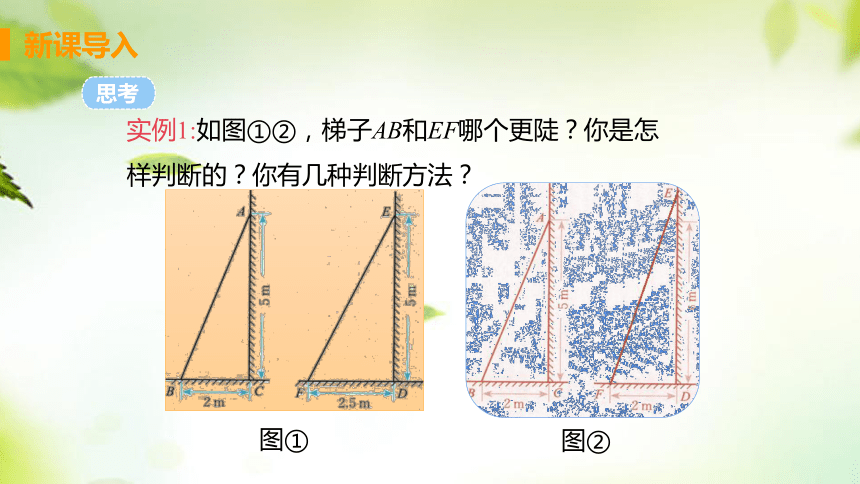
实例1:如图①②,梯子AB和EF哪个更陡?你是怎样判断的?你有几种判断方法?
图①
图②
新课导入
思考
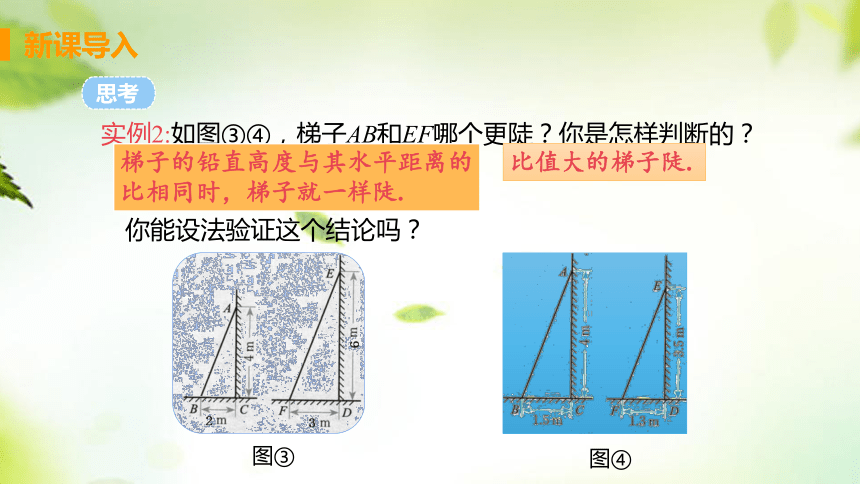
实例2:如图③④,梯子AB和EF哪个更陡?你是怎样判断的?
梯子的铅直高度与其水平距离的比相同时,梯子就一样陡.
比值大的梯子陡.
你能设法验证这个结论吗?
图③
图④
新课讲解
知识点1 正切的定义
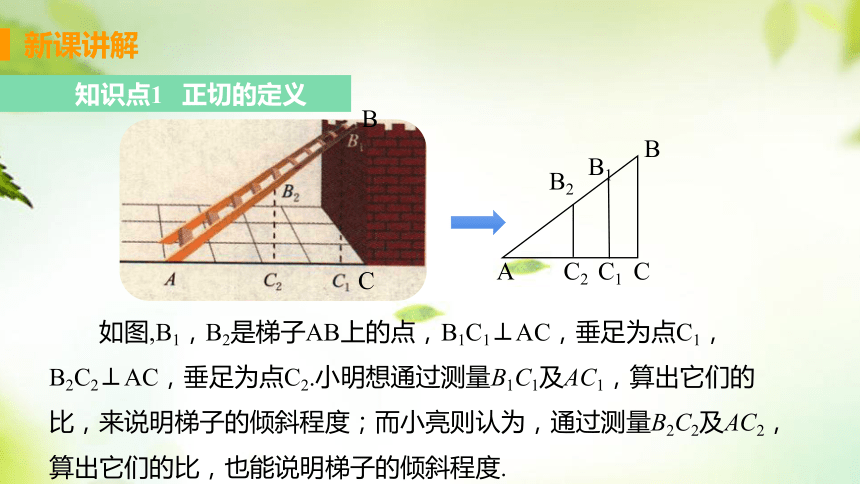
如图,B1,B2是梯子AB上的点,B1C1⊥AC,垂足为点C1,B2C2⊥AC,垂足为点C2.小明想通过测量B1C1及AC1,算出它们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子的倾斜程度.
A
B1
C2
C1
B2
B
C
C
B
新课讲解
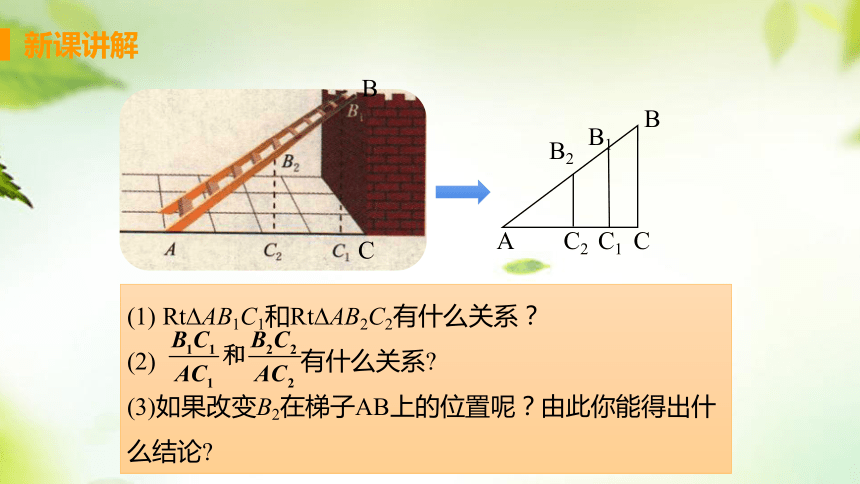
(1) Rt AB1C1和Rt AB2C2有什么关系?
(2) 有什么关系
(3)如果改变B2在梯子AB上的位置呢?由此你能得出什么结论
A
B1
C2
C1
B2
B
C
C
B
新课讲解
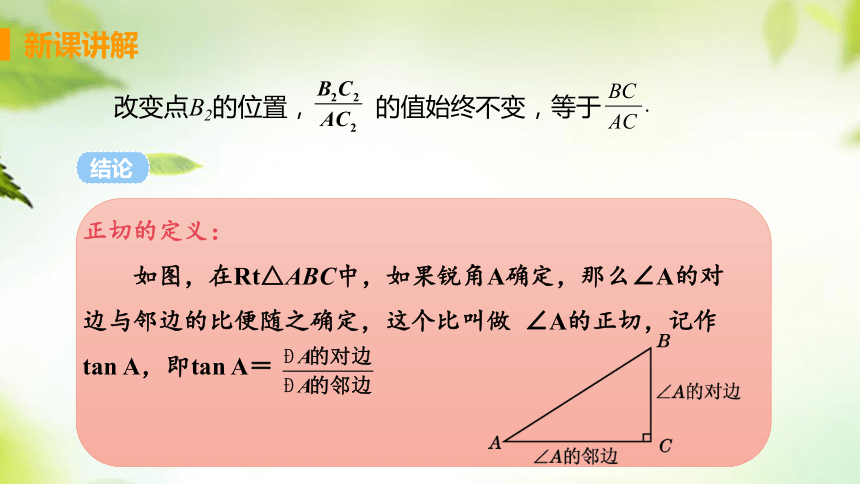
改变点B2的位置, 的值始终不变,等于
正切的定义:
如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做 ∠A的正切,记作tan A,即tan A=
结论
新课讲解
定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3) tanA没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序).
4)tanA不表示“tan”乘以“A ”.
5) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关
新课讲解
知识点2 正切的应用
如图,梯子AB的倾斜程度与tanA有怎样的关系
B
C
1.当梯子与地面所成的角为锐角A时,tanA=
tanA的值越大,梯子越陡.
因此可用梯子的倾斜角的正切值来描述梯子的倾斜程度.
2.当倾斜角确定时,其对边与邻边之比随之确定,这一比值只与
倾斜角的大小有关,而与物体的长度无关.
新课讲解
知识点3 坡度和坡角
1.坡面与水平面的夹角(α)叫坡角。
2.坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切。
3.坡度越大,坡面越陡。
如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:
100m
60m
┌
α
i
课堂小结
正切
正切的概念
正切与坡度(角)的关系
当堂小练
2、在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tan B的值是( )
A. B.3 C. D.
3、 一个直角三角形中,如果各边的长度都扩大为原来的2倍,那么它的两个锐角的正切值( )
A.都没有变化 B.都扩大为原来的2倍
C.都缩小为原来的一半 D.不能确定是否发生变化
D
A
拓展与延伸
如图,铁路路基横断面为一个四边形,其中AD∥BC.
若两斜坡的坡度均为i=2∶3,顶宽是3 m,路基高是
4 m,则路基的下底宽是( )
A.7 m B.9 m C.12 m D.15 m
D
如图,在Rt△ABC中,如果锐角A确定,那么∠A的 _
与 的比便随之确定,这个比叫做∠A的正切,记作tan A,即tan A= .
邻边
正切的定义
对边
注意:当锐角A变化时,tan A的值也随之变化.
1.(1)如图1,tan A= ,tan B= .
图1 图2
(2)(北师9下P4改编、人教9下P65改编)如图2,在Rt△ABC中,∠C=90°,BC=1,AC=2,则tan α等于( )
A B.2 C D
A
tan A的值越 ,梯子越陡(如图).
正切的性质
大
A B C D
2.(北师9下P2改编)如图,下面四个梯子最陡的是( )
B
(1)正切在日常生活中的应用很广泛,例如:建筑、工程技术等.正切经常用来描述山坡的坡度、堤坝的坡度.
(2)坡度的定义:如图,坡面的 与 的比称为坡度(或坡比,用字母i表示),i=tan α= .
水平宽度
坡度
铅直高度
.(新题速递)冬天哈尔滨的冰雪旅游是继夏天的淄博烧烤之后的新旅游热点,南方游客纷纷打卡哈尔滨冰雪大世界.如图,已知某滑雪坡道AB的坡度是1∶3,坡道的水平宽度是30米,则高BC为 米.
10
A.tan α的值越大,梯子越缓
B.tan α的值越小,梯子越陡
C.tan α的值越大,梯子越陡
D.梯子的陡缓程度与α的正切值无关
5.【例2】如图,梯子(长度不变)和地面所成的锐角为α.关于α的正切值与梯子的倾斜程度的关系,下列叙述正确的是
( )
C
A.12 m B.4 m
C.5 m D.6 m
6.【例3】某河堤横断面如图,堤高BC=6 m,迎水坡AB的坡比为1∶,则AB的长为( )
A
7.【例4】(北师9下P3改编)如图,方方和圆圆分别将两根木棒AB,CD斜靠在墙AE上,其中AB=10 cm,CD=6 cm,BE=6 cm,DE=2 cm.你能判断谁的木棒更陡吗?并说明理由.
解:圆圆的木棒CD更陡.理由如下:
在Rt△ABE中,AE==8(cm),
∴tan∠ABE=
在Rt△CDE中,CE==4 (cm),
∴tan∠CDE==2 <2 ,即tan∠CDE>tan∠ABE,
∴圆圆的木棒CD更陡.
8.(北师9下P3改编)如图是甲、乙两个自动扶梯, 自动扶梯比较陡(填“甲”或“乙”).
乙
A.36 m B.24 m C.12 m D.6 m
9.如图,一座公路桥离地面高度AC为6 m,引桥AB的水平宽度BC为24 m,为降低坡度,现决定将引桥坡面改为AD,使其坡度为1∶6,则BD的长是( )
C
请完成本课课后对应习题
布置作业
THANKS
北师大版九年级数学下册课件
第一章 直角三角形的边角关系
1 锐角三角函数
课时1 正切
1.理解正切的意义和与现实生活的联系.
2.能够用 表示直角三角形中两直角边的比,表示生活中
物体的倾斜程度、坡度(坡比)等.(重点)
3.能够根据直角三角形的边角关系,用正切进行简单的计
算.(难点)
学习目标
新课导入
生活中的梯子
梯子是我们日常生活中常见的物体.
新课导入
思考
实例1:如图①②,梯子AB和EF哪个更陡?你是怎样判断的?你有几种判断方法?
图①
图②
新课导入
思考
实例2:如图③④,梯子AB和EF哪个更陡?你是怎样判断的?
梯子的铅直高度与其水平距离的比相同时,梯子就一样陡.
比值大的梯子陡.
你能设法验证这个结论吗?
图③
图④
新课讲解
知识点1 正切的定义
如图,B1,B2是梯子AB上的点,B1C1⊥AC,垂足为点C1,B2C2⊥AC,垂足为点C2.小明想通过测量B1C1及AC1,算出它们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量B2C2及AC2,算出它们的比,也能说明梯子的倾斜程度.
A
B1
C2
C1
B2
B
C
C
B
新课讲解
(1) Rt AB1C1和Rt AB2C2有什么关系?
(2) 有什么关系
(3)如果改变B2在梯子AB上的位置呢?由此你能得出什么结论
A
B1
C2
C1
B2
B
C
C
B
新课讲解
改变点B2的位置, 的值始终不变,等于
正切的定义:
如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做 ∠A的正切,记作tan A,即tan A=
结论
新课讲解
定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的, ∠A是一个锐角.
2) tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”。但∠BAC的正切表示为:tan∠BAC,∠1的正切表示为:tan∠1.
3) tanA没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序).
4)tanA不表示“tan”乘以“A ”.
5) tanA的大小只与∠A的大小有关,而与直角三角形的边长无关
新课讲解
知识点2 正切的应用
如图,梯子AB的倾斜程度与tanA有怎样的关系
B
C
1.当梯子与地面所成的角为锐角A时,tanA=
tanA的值越大,梯子越陡.
因此可用梯子的倾斜角的正切值来描述梯子的倾斜程度.
2.当倾斜角确定时,其对边与邻边之比随之确定,这一比值只与
倾斜角的大小有关,而与物体的长度无关.
新课讲解
知识点3 坡度和坡角
1.坡面与水平面的夹角(α)叫坡角。
2.坡面的铅直高度与水平宽度的比称为坡度i(或坡比),即坡度等于坡角的正切。
3.坡度越大,坡面越陡。
如图,正切也经常用来描述山坡的坡度.例如,有一山坡在水平方向上每前进100m就升高60m,那么山坡的坡度i(即tanα)就是:
100m
60m
┌
α
i
课堂小结
正切
正切的概念
正切与坡度(角)的关系
当堂小练
2、在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tan B的值是( )
A. B.3 C. D.
3、 一个直角三角形中,如果各边的长度都扩大为原来的2倍,那么它的两个锐角的正切值( )
A.都没有变化 B.都扩大为原来的2倍
C.都缩小为原来的一半 D.不能确定是否发生变化
D
A
拓展与延伸
如图,铁路路基横断面为一个四边形,其中AD∥BC.
若两斜坡的坡度均为i=2∶3,顶宽是3 m,路基高是
4 m,则路基的下底宽是( )
A.7 m B.9 m C.12 m D.15 m
D
如图,在Rt△ABC中,如果锐角A确定,那么∠A的 _
与 的比便随之确定,这个比叫做∠A的正切,记作tan A,即tan A= .
邻边
正切的定义
对边
注意:当锐角A变化时,tan A的值也随之变化.
1.(1)如图1,tan A= ,tan B= .
图1 图2
(2)(北师9下P4改编、人教9下P65改编)如图2,在Rt△ABC中,∠C=90°,BC=1,AC=2,则tan α等于( )
A B.2 C D
A
tan A的值越 ,梯子越陡(如图).
正切的性质
大
A B C D
2.(北师9下P2改编)如图,下面四个梯子最陡的是( )
B
(1)正切在日常生活中的应用很广泛,例如:建筑、工程技术等.正切经常用来描述山坡的坡度、堤坝的坡度.
(2)坡度的定义:如图,坡面的 与 的比称为坡度(或坡比,用字母i表示),i=tan α= .
水平宽度
坡度
铅直高度
.(新题速递)冬天哈尔滨的冰雪旅游是继夏天的淄博烧烤之后的新旅游热点,南方游客纷纷打卡哈尔滨冰雪大世界.如图,已知某滑雪坡道AB的坡度是1∶3,坡道的水平宽度是30米,则高BC为 米.
10
A.tan α的值越大,梯子越缓
B.tan α的值越小,梯子越陡
C.tan α的值越大,梯子越陡
D.梯子的陡缓程度与α的正切值无关
5.【例2】如图,梯子(长度不变)和地面所成的锐角为α.关于α的正切值与梯子的倾斜程度的关系,下列叙述正确的是
( )
C
A.12 m B.4 m
C.5 m D.6 m
6.【例3】某河堤横断面如图,堤高BC=6 m,迎水坡AB的坡比为1∶,则AB的长为( )
A
7.【例4】(北师9下P3改编)如图,方方和圆圆分别将两根木棒AB,CD斜靠在墙AE上,其中AB=10 cm,CD=6 cm,BE=6 cm,DE=2 cm.你能判断谁的木棒更陡吗?并说明理由.
解:圆圆的木棒CD更陡.理由如下:
在Rt△ABE中,AE==8(cm),
∴tan∠ABE=
在Rt△CDE中,CE==4 (cm),
∴tan∠CDE==2 <2 ,即tan∠CDE>tan∠ABE,
∴圆圆的木棒CD更陡.
8.(北师9下P3改编)如图是甲、乙两个自动扶梯, 自动扶梯比较陡(填“甲”或“乙”).
乙
A.36 m B.24 m C.12 m D.6 m
9.如图,一座公路桥离地面高度AC为6 m,引桥AB的水平宽度BC为24 m,为降低坡度,现决定将引桥坡面改为AD,使其坡度为1∶6,则BD的长是( )
C
请完成本课课后对应习题
布置作业
THANKS
