2024-2025学年北师大版九年级数学下册 1.1 锐角三角函数(2) 正弦和余弦 课件 (共24张PPT)
文档属性
| 名称 | 2024-2025学年北师大版九年级数学下册 1.1 锐角三角函数(2) 正弦和余弦 课件 (共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 615.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 16:11:58 | ||
图片预览






文档简介
(共24张PPT)
北师大版九年级数学下册课件
第一章 直角三角形的边角关系
1 锐角三角函数
课时2 正弦和余弦
1.能利用相似的直角三角形,探索并认识锐角三角函数——正弦、余弦,理解锐角的正弦与余弦和梯子倾斜程度的关系.(重点)
2.能够用sinA,cosA表示直角三角形中直角边与斜边的比,能够用正弦、余弦进行简单的计算.(难点)
学习目标
新课讲解
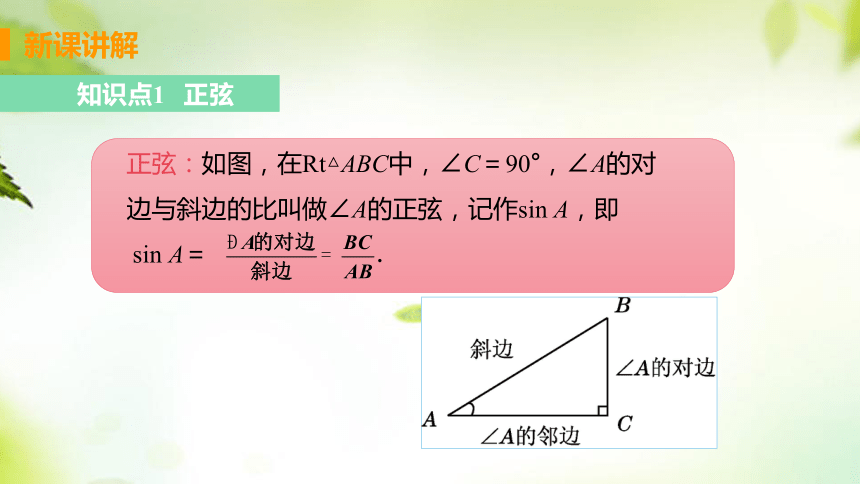
知识点1 正弦
正弦:如图,在Rt△ABC中,∠C=90°,∠A的对
边与斜边的比叫做∠A的正弦,记作sin A,即
sin A=
新课讲解
知识点2 余弦
余弦:如图,在Rt△ABC中,∠C=90°,∠A的邻
边与斜边的比叫做∠A的余弦,记作cos A,
即cos A=
新课讲解
定义中应该注意的几个问题:
1.sinA,cosA,tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA各是一个完整的符号,分别表示∠A的正弦、余弦和正切,记号中习惯省去“∠”;
3.sinA,cosA,tanA分别是一个比值.注意比的顺序,且在直角三角形中sinA,cosA,tanA均大于0,无单位.
4.sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
课堂小结
正弦和余弦
正弦的概念
余弦的概念
当堂小练
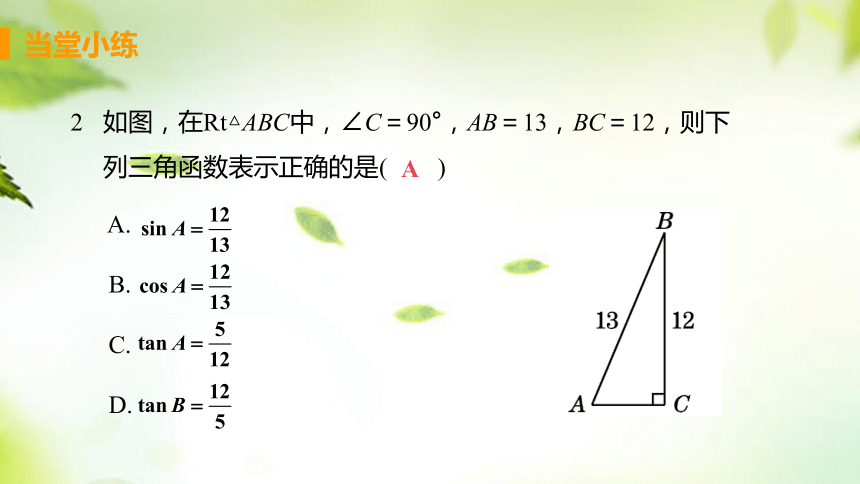
如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
A.
B.
C.
D.
A
当堂小练
已知在Rt△ABC中,∠C=90°,如果BC=2,∠A=α,则AC的长为( )
A.2sin α
B.2cos α
C.2tan α
D.
D
(2)如图,在Rt△ABC中,∠A的 与 的比叫做∠A的余弦,记作cos A,即cos A= .
斜边
正弦和余弦的定义
邻边
(1)如图,在Rt△ABC中,∠A的 与 的比叫做∠A的正弦,记作sin A,即sin A= .
斜边
对边
1.(1)(人教9下P63)如图,在Rt△ABC中,∠C=90°,则:
①sin A= ;②sin B= ;
③cos A= ;④cos B= ;
(2)在Rt△ABC中,∠C=90°,AB=,BC=,则sin A= ,cos A= .
三角函数的定义
(1)锐角A的正弦、余弦和正切都是∠A的三角函数.
(2)锐角三角函数的本质是两条线段长度的比,没有单位,其大小只与锐角的大小有关,与锐角所在直角三角形的大小无关.
2.(人教9下P65)把△ABC三边的长度都扩大为原来的2倍,则锐角A的正弦函数值( )
A.不变 B.扩大为原来的2倍
C.缩小为原来的 D.不能确定
A
求锐角的三角函数值
在直角三角形中,运用三角函数的定义求锐角三角函数值.
注意:求锐角三角函数值时,必须在直角三角形中进行,若无直角三角形,则要先构造直角三角形.
3.(2024深圳一模)正方形网格中,∠AOB如图放置,则tan∠AOB的值为 .
2
4.【例1】(人教9下P65)(2023攀枝花改编)如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sin A及cos B的值.
解:在Rt△ABC中,∠C=90°,AB=10,BC=6,
所以sin A=,cos B=
小结:先根据勾股定理求出所需的第三边长,然后利用定义求锐角三角函数值,未给出图形时要作出草图.
小结:由锐角三角函数的定义及勾股定理即可求出未知边长.
5.【例2】在Rt△ABC中,∠C=90°,cos B=,AB=15,则BC的长是( )
A.3 B.6 C.9 D.12
C
6.【例3】(2023益阳)如图,在平面直角坐标系xOy中,
A(0,1),B(4,1),C(5,6),则sin∠BAC= .
小结:根据锐角三角函数的定义,需先构造直角三角形.
7.【例4】(北师9下P6改编)如图,在△ABC中,AB=AC=6,BC=8,AD⊥BC于点D.
(1)求AD的长;
(2)求sin B,cos C的值.
解:(1)∵AB=AC,AD⊥BC,∴BD=CD=BC=8=4.
∴AD==2
(2)sin B=,cos C=
8.(北师9下P6改编、人教9下P65改编)在Rt△ABC中,∠C=90°,AC=2,AB=3,请按定义求出∠A的三个三角函数值.
解:在Rt△ABC中,由勾股定理得
BC=,
所以sin A=,cos A=,tan A=
9.在Rt△ABC中,∠C=90°,sin A=,AC=6 cm,则BC的长度为( )
A.6 cm B.7 cm C.8 cm D.9 cm
C
A B
C.2 D.2
10.如图,△ABC的顶点在正方形网格的格点上,则tan A的值为( )
A
请完成本节课后对应习题
布置作业
THANKS
北师大版九年级数学下册课件
第一章 直角三角形的边角关系
1 锐角三角函数
课时2 正弦和余弦
1.能利用相似的直角三角形,探索并认识锐角三角函数——正弦、余弦,理解锐角的正弦与余弦和梯子倾斜程度的关系.(重点)
2.能够用sinA,cosA表示直角三角形中直角边与斜边的比,能够用正弦、余弦进行简单的计算.(难点)
学习目标
新课讲解
知识点1 正弦
正弦:如图,在Rt△ABC中,∠C=90°,∠A的对
边与斜边的比叫做∠A的正弦,记作sin A,即
sin A=
新课讲解
知识点2 余弦
余弦:如图,在Rt△ABC中,∠C=90°,∠A的邻
边与斜边的比叫做∠A的余弦,记作cos A,
即cos A=
新课讲解
定义中应该注意的几个问题:
1.sinA,cosA,tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA各是一个完整的符号,分别表示∠A的正弦、余弦和正切,记号中习惯省去“∠”;
3.sinA,cosA,tanA分别是一个比值.注意比的顺序,且在直角三角形中sinA,cosA,tanA均大于0,无单位.
4.sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
课堂小结
正弦和余弦
正弦的概念
余弦的概念
当堂小练
如图,在Rt△ABC中,∠C=90°,AB=13,BC=12,则下列三角函数表示正确的是( )
A.
B.
C.
D.
A
当堂小练
已知在Rt△ABC中,∠C=90°,如果BC=2,∠A=α,则AC的长为( )
A.2sin α
B.2cos α
C.2tan α
D.
D
(2)如图,在Rt△ABC中,∠A的 与 的比叫做∠A的余弦,记作cos A,即cos A= .
斜边
正弦和余弦的定义
邻边
(1)如图,在Rt△ABC中,∠A的 与 的比叫做∠A的正弦,记作sin A,即sin A= .
斜边
对边
1.(1)(人教9下P63)如图,在Rt△ABC中,∠C=90°,则:
①sin A= ;②sin B= ;
③cos A= ;④cos B= ;
(2)在Rt△ABC中,∠C=90°,AB=,BC=,则sin A= ,cos A= .
三角函数的定义
(1)锐角A的正弦、余弦和正切都是∠A的三角函数.
(2)锐角三角函数的本质是两条线段长度的比,没有单位,其大小只与锐角的大小有关,与锐角所在直角三角形的大小无关.
2.(人教9下P65)把△ABC三边的长度都扩大为原来的2倍,则锐角A的正弦函数值( )
A.不变 B.扩大为原来的2倍
C.缩小为原来的 D.不能确定
A
求锐角的三角函数值
在直角三角形中,运用三角函数的定义求锐角三角函数值.
注意:求锐角三角函数值时,必须在直角三角形中进行,若无直角三角形,则要先构造直角三角形.
3.(2024深圳一模)正方形网格中,∠AOB如图放置,则tan∠AOB的值为 .
2
4.【例1】(人教9下P65)(2023攀枝花改编)如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sin A及cos B的值.
解:在Rt△ABC中,∠C=90°,AB=10,BC=6,
所以sin A=,cos B=
小结:先根据勾股定理求出所需的第三边长,然后利用定义求锐角三角函数值,未给出图形时要作出草图.
小结:由锐角三角函数的定义及勾股定理即可求出未知边长.
5.【例2】在Rt△ABC中,∠C=90°,cos B=,AB=15,则BC的长是( )
A.3 B.6 C.9 D.12
C
6.【例3】(2023益阳)如图,在平面直角坐标系xOy中,
A(0,1),B(4,1),C(5,6),则sin∠BAC= .
小结:根据锐角三角函数的定义,需先构造直角三角形.
7.【例4】(北师9下P6改编)如图,在△ABC中,AB=AC=6,BC=8,AD⊥BC于点D.
(1)求AD的长;
(2)求sin B,cos C的值.
解:(1)∵AB=AC,AD⊥BC,∴BD=CD=BC=8=4.
∴AD==2
(2)sin B=,cos C=
8.(北师9下P6改编、人教9下P65改编)在Rt△ABC中,∠C=90°,AC=2,AB=3,请按定义求出∠A的三个三角函数值.
解:在Rt△ABC中,由勾股定理得
BC=,
所以sin A=,cos A=,tan A=
9.在Rt△ABC中,∠C=90°,sin A=,AC=6 cm,则BC的长度为( )
A.6 cm B.7 cm C.8 cm D.9 cm
C
A B
C.2 D.2
10.如图,△ABC的顶点在正方形网格的格点上,则tan A的值为( )
A
请完成本节课后对应习题
布置作业
THANKS
