3.1.1 圆柱的认识(同步练习)(含答案)-2024-2025学年六年级数学下册(人教版)
文档属性
| 名称 | 3.1.1 圆柱的认识(同步练习)(含答案)-2024-2025学年六年级数学下册(人教版) |
|
|
| 格式 | docx | ||
| 文件大小 | 264.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 00:00:00 | ||
图片预览

文档简介
3.1 圆柱的认识(同步练习)
一、单选题
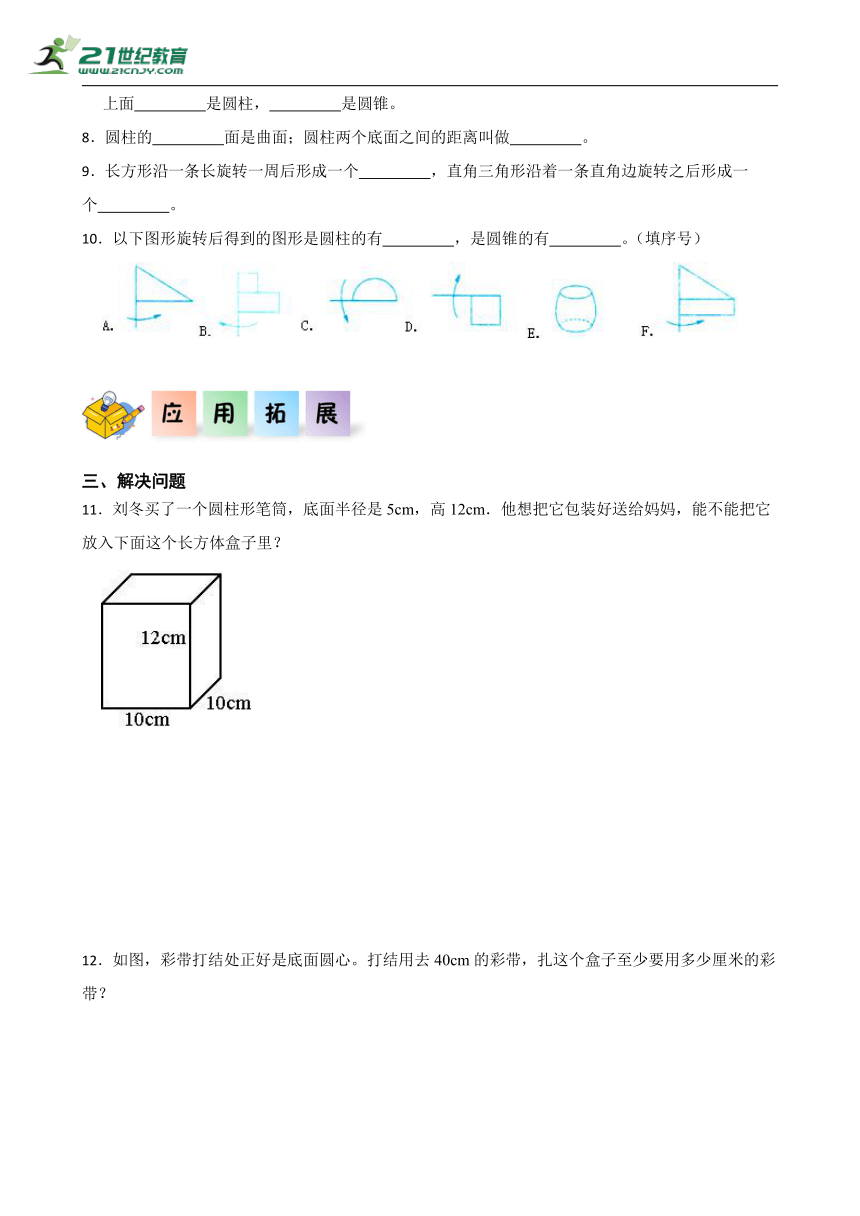
1.分别把下面的立体图形竖切,截面是长方形的是( )。
A. B. C.
2.下列各图中,h表示圆柱的高的是( )
A. B. C.
3.圆柱的体积公式推导过程,将圆柱切拼成一个近似的长方体后,( )。
A.表面积不变,体积不变 B.表面积变大,体积不变
C.表面积变大,体积变大 D.表面积变小,体积变小
4.图形( )是圆柱。
A. B. C.
5.以下说法中正确的是( )
A.只要上下两个底面大小相同就是圆柱。
B.将一个圆柱沿着底面直径切成两半,得到的截面可能是正方形。
C.圆锥的侧面是平面。
二、填空题
6.一个长方形的长是5cm,宽是3cm,以它的短边为轴旋转一周得到圆柱,圆柱的底面积是 cm2,表面积是 cm2。
7.
上面 是圆柱, 是圆锥。
8.圆柱的 面是曲面;圆柱两个底面之间的距离叫做 。
9.长方形沿一条长旋转一周后形成一个 ,直角三角形沿着一条直角边旋转之后形成一个 。
10.以下图形旋转后得到的图形是圆柱的有 ,是圆锥的有 。(填序号)
三、解决问题
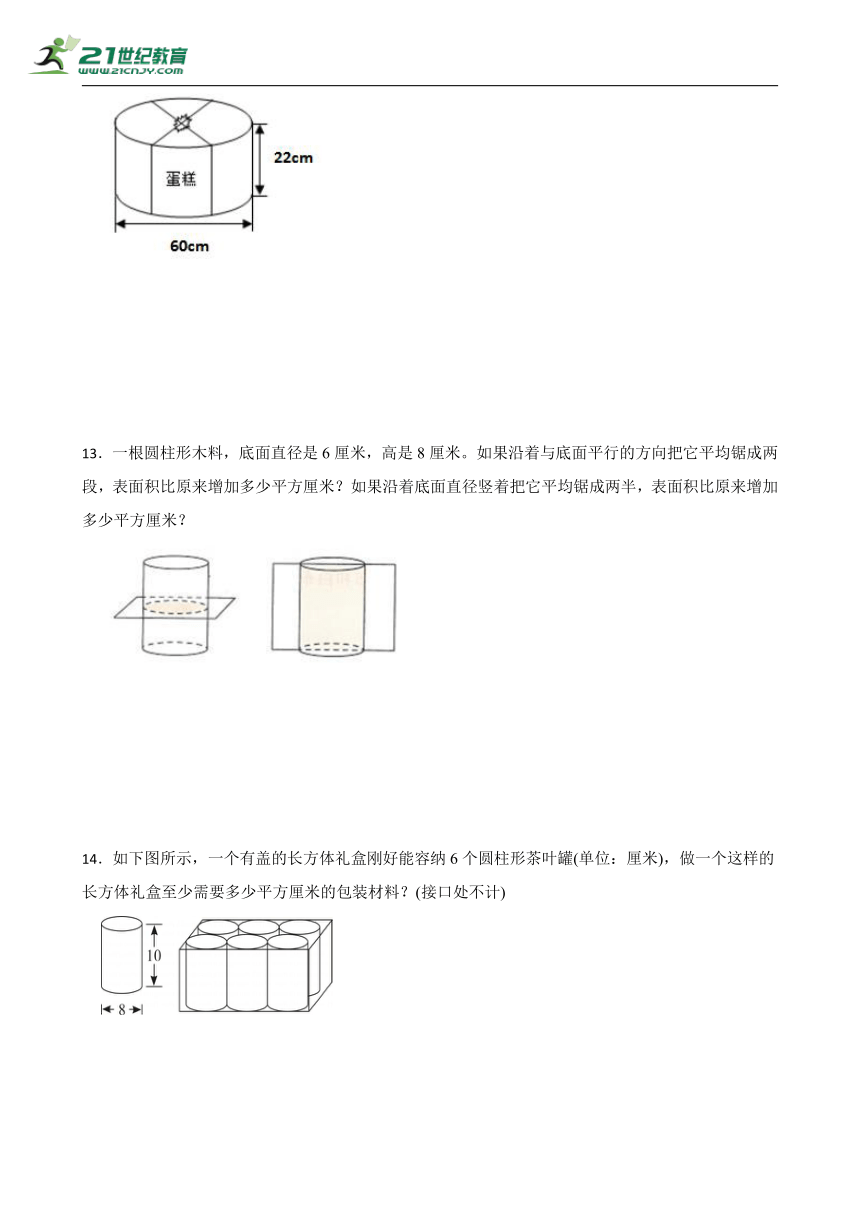
11.刘冬买了一个圆柱形笔筒,底面半径是5cm,高12cm.他想把它包装好送给妈妈,能不能把它放入下面这个长方体盒子里?
12.如图,彩带打结处正好是底面圆心。打结用去40cm的彩带,扎这个盒子至少要用多少厘米的彩带?
13.一根圆柱形木料,底面直径是6厘米,高是8厘米。如果沿着与底面平行的方向把它平均锯成两段,表面积比原来增加多少平方厘米?如果沿着底面直径竖着把它平均锯成两半,表面积比原来增加多少平方厘米?
14.如下图所示,一个有盖的长方体礼盒刚好能容纳6个圆柱形茶叶罐(单位:厘米),做一个这样的长方体礼盒至少需要多少平方厘米的包装材料?(接口处不计)
答案解析部分
1.B
解:A项:截面是梯形;
B项:截面是长方形;
C项:截面是三角形。
故答案为:B。
如图沿着圆柱体竖切,截面是长方形。
2.A
中的h是圆柱的高,所以答案选A;
故答案为:A。
一定要清楚圆柱的高是两个底面之间的距离,并且高垂直于两个底面,而且高可以画无数条。
3.B
将圆柱切拼成一个近似的长方体后,表面积变大,体积不变。
故答案为:B。
将圆柱切拼成一个近似的长方体,表面积增加了两个以底面半径和高为边长的长方形的面,所以表面积变大;圆柱的底面积等于长方体的底面积,圆柱的高等于长方体的高,圆柱的体积等于长方体的体积,所以体积不变。
4.B
解:第二个图形是圆柱。
故答案为:B。
圆柱整体粗细一样,两头是圆形,例如铅笔、水杯等。
5.B
解:选项A,上下两个底面大小相同,且互相平行才能是圆柱,即错误;
选项B,圆柱的底面直径和圆柱的高相等,则横截面是正方形,即正确;
选项C,圆柱的侧面是曲面,即错误。
故答案为:B。
圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。它有2个大小相同、相互平行的圆形底面和1个曲面侧面。其侧面展开是矩形。
圆锥的侧面是扇形,是一个曲面,本题据此进行解答。
6.78.5;188.4
解:底面积:3.14×52
=3.14×25
=78.5(平方厘米);
表面积:3.14×2×5+78.5×2
=31.4+157
=188.4(平方厘米);
故答案为:78.5;188.4。
以它的短边为轴旋转一周得到圆柱,圆柱的底面半径就等于长方形的长,圆柱的高就等于长方形的宽,再根据圆柱底面积=π×半径2,圆柱表面积=侧面积+底面积×2=圆柱底面周长×高+底面积×2,代入数值计算即可。
7.③、⑤;①
解:③、⑤是圆柱;①是圆锥。
故答案为:③、⑤;①。
像③、⑤一样直直的、上下一样粗细、能滚动的物体,在数学上叫做圆柱;像①一样由一个圆和一个曲面组成的立体图形是圆锥。
8.侧;高
解:圆柱的侧面是曲面;圆柱两个底面之间的距离叫做高。
故答案为:侧;高。
当底面周长和高相等时,圆柱的侧面展开图是一个正方形;当底面周长和高不相等时,圆柱的侧面展开图是一个长方形;当沿着侧面斜着剪开时,圆柱的侧面是一个平行四边形。
9.圆柱;圆锥
解:长方形沿一条长旋转一周后形成一个圆柱;直角三角形沿着一条直角边旋转之后形成圆锥。
故答案为:圆柱;圆锥。
圆锥的定义是:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥。
以矩形的一边所在直线为旋转轴,其余三边旋转360°形成的面所围成的旋转体,即AG矩形的内一条边为轴,旋转360°所得的几何体就是圆柱。
本题据此解答。
10.D;A
解:旋转后得到的图形是圆柱的有正方形,是圆锥的有三角形。
故答案为:D;A。
三角形旋转后得到的图形是圆锥,长方形或正方形旋转后得到的图形是圆柱。
11.解:可以
圆柱的底面直径:5×2=10(cm),圆柱的底面直径等于长方体的长、宽,圆柱的高等于长方体的高,可以把圆柱体放到长方体盒子里.
答:可以把它放入下面这个长方体盒子里.
根据题意可知,要求能不能把圆柱放入这个长方体盒子里,比较长方体的长、宽和圆柱的底面直径,圆柱的高和长方体的高的关系即可解答.
12.22×4+60×4+40=368(厘米)
答:扎这个盒子至少要用368厘米的彩带。
题图结合可知,扎这个盒子的彩带可分为3部分,一是与圆柱的高相等的有4段,二是与圆柱的底面直径相等的有4段,三是打结用去的彩带,求出三部分彩带长度后加起来即可。
13.左图:3.14×(6÷2)2×2=56.52(平方厘米)
答:如果沿着与底面平行的方向把它平均锯成两半,表面积比原来增加56.52平方厘米。
右图:6×8×2=96(平方厘米)
答:如果沿着底面直径竖着把它平均锯成两半,表面积比原来增加96平方厘米。
如果沿着与底面平行的方向把它平均锯成两段,表面积比原来增加了两个底面积,底面直径÷2=底面半径,π×底面半径的平方×2=增加的面积;
如果沿着底面直径竖着把它平均锯成两半,表面积比原来增加了两个长方形的面积,长方形的长是圆柱的底面直径,长方形的宽是圆柱的高,长×宽×2=增加的面积。
14.解:8×3=24(厘米),8×2=16(厘米)
(24×16+24×10+10×16)×2
=(384+240+160)×2
=784×2
=1568(平方厘米)
答: 做一个这样的长方体礼盒至少需要1568平方厘米的包装材料。
根据题意,长方体的长=直径×3,长方体的高=10厘米,长方宽=直径×2,再根据长方体的表面积=(长×宽+长×高+宽×高)×2;据此解答。
一、单选题
1.分别把下面的立体图形竖切,截面是长方形的是( )。
A. B. C.
2.下列各图中,h表示圆柱的高的是( )
A. B. C.
3.圆柱的体积公式推导过程,将圆柱切拼成一个近似的长方体后,( )。
A.表面积不变,体积不变 B.表面积变大,体积不变
C.表面积变大,体积变大 D.表面积变小,体积变小
4.图形( )是圆柱。
A. B. C.
5.以下说法中正确的是( )
A.只要上下两个底面大小相同就是圆柱。
B.将一个圆柱沿着底面直径切成两半,得到的截面可能是正方形。
C.圆锥的侧面是平面。
二、填空题
6.一个长方形的长是5cm,宽是3cm,以它的短边为轴旋转一周得到圆柱,圆柱的底面积是 cm2,表面积是 cm2。
7.
上面 是圆柱, 是圆锥。
8.圆柱的 面是曲面;圆柱两个底面之间的距离叫做 。
9.长方形沿一条长旋转一周后形成一个 ,直角三角形沿着一条直角边旋转之后形成一个 。
10.以下图形旋转后得到的图形是圆柱的有 ,是圆锥的有 。(填序号)
三、解决问题
11.刘冬买了一个圆柱形笔筒,底面半径是5cm,高12cm.他想把它包装好送给妈妈,能不能把它放入下面这个长方体盒子里?
12.如图,彩带打结处正好是底面圆心。打结用去40cm的彩带,扎这个盒子至少要用多少厘米的彩带?
13.一根圆柱形木料,底面直径是6厘米,高是8厘米。如果沿着与底面平行的方向把它平均锯成两段,表面积比原来增加多少平方厘米?如果沿着底面直径竖着把它平均锯成两半,表面积比原来增加多少平方厘米?
14.如下图所示,一个有盖的长方体礼盒刚好能容纳6个圆柱形茶叶罐(单位:厘米),做一个这样的长方体礼盒至少需要多少平方厘米的包装材料?(接口处不计)
答案解析部分
1.B
解:A项:截面是梯形;
B项:截面是长方形;
C项:截面是三角形。
故答案为:B。
如图沿着圆柱体竖切,截面是长方形。
2.A
中的h是圆柱的高,所以答案选A;
故答案为:A。
一定要清楚圆柱的高是两个底面之间的距离,并且高垂直于两个底面,而且高可以画无数条。
3.B
将圆柱切拼成一个近似的长方体后,表面积变大,体积不变。
故答案为:B。
将圆柱切拼成一个近似的长方体,表面积增加了两个以底面半径和高为边长的长方形的面,所以表面积变大;圆柱的底面积等于长方体的底面积,圆柱的高等于长方体的高,圆柱的体积等于长方体的体积,所以体积不变。
4.B
解:第二个图形是圆柱。
故答案为:B。
圆柱整体粗细一样,两头是圆形,例如铅笔、水杯等。
5.B
解:选项A,上下两个底面大小相同,且互相平行才能是圆柱,即错误;
选项B,圆柱的底面直径和圆柱的高相等,则横截面是正方形,即正确;
选项C,圆柱的侧面是曲面,即错误。
故答案为:B。
圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。它有2个大小相同、相互平行的圆形底面和1个曲面侧面。其侧面展开是矩形。
圆锥的侧面是扇形,是一个曲面,本题据此进行解答。
6.78.5;188.4
解:底面积:3.14×52
=3.14×25
=78.5(平方厘米);
表面积:3.14×2×5+78.5×2
=31.4+157
=188.4(平方厘米);
故答案为:78.5;188.4。
以它的短边为轴旋转一周得到圆柱,圆柱的底面半径就等于长方形的长,圆柱的高就等于长方形的宽,再根据圆柱底面积=π×半径2,圆柱表面积=侧面积+底面积×2=圆柱底面周长×高+底面积×2,代入数值计算即可。
7.③、⑤;①
解:③、⑤是圆柱;①是圆锥。
故答案为:③、⑤;①。
像③、⑤一样直直的、上下一样粗细、能滚动的物体,在数学上叫做圆柱;像①一样由一个圆和一个曲面组成的立体图形是圆锥。
8.侧;高
解:圆柱的侧面是曲面;圆柱两个底面之间的距离叫做高。
故答案为:侧;高。
当底面周长和高相等时,圆柱的侧面展开图是一个正方形;当底面周长和高不相等时,圆柱的侧面展开图是一个长方形;当沿着侧面斜着剪开时,圆柱的侧面是一个平行四边形。
9.圆柱;圆锥
解:长方形沿一条长旋转一周后形成一个圆柱;直角三角形沿着一条直角边旋转之后形成圆锥。
故答案为:圆柱;圆锥。
圆锥的定义是:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥。
以矩形的一边所在直线为旋转轴,其余三边旋转360°形成的面所围成的旋转体,即AG矩形的内一条边为轴,旋转360°所得的几何体就是圆柱。
本题据此解答。
10.D;A
解:旋转后得到的图形是圆柱的有正方形,是圆锥的有三角形。
故答案为:D;A。
三角形旋转后得到的图形是圆锥,长方形或正方形旋转后得到的图形是圆柱。
11.解:可以
圆柱的底面直径:5×2=10(cm),圆柱的底面直径等于长方体的长、宽,圆柱的高等于长方体的高,可以把圆柱体放到长方体盒子里.
答:可以把它放入下面这个长方体盒子里.
根据题意可知,要求能不能把圆柱放入这个长方体盒子里,比较长方体的长、宽和圆柱的底面直径,圆柱的高和长方体的高的关系即可解答.
12.22×4+60×4+40=368(厘米)
答:扎这个盒子至少要用368厘米的彩带。
题图结合可知,扎这个盒子的彩带可分为3部分,一是与圆柱的高相等的有4段,二是与圆柱的底面直径相等的有4段,三是打结用去的彩带,求出三部分彩带长度后加起来即可。
13.左图:3.14×(6÷2)2×2=56.52(平方厘米)
答:如果沿着与底面平行的方向把它平均锯成两半,表面积比原来增加56.52平方厘米。
右图:6×8×2=96(平方厘米)
答:如果沿着底面直径竖着把它平均锯成两半,表面积比原来增加96平方厘米。
如果沿着与底面平行的方向把它平均锯成两段,表面积比原来增加了两个底面积,底面直径÷2=底面半径,π×底面半径的平方×2=增加的面积;
如果沿着底面直径竖着把它平均锯成两半,表面积比原来增加了两个长方形的面积,长方形的长是圆柱的底面直径,长方形的宽是圆柱的高,长×宽×2=增加的面积。
14.解:8×3=24(厘米),8×2=16(厘米)
(24×16+24×10+10×16)×2
=(384+240+160)×2
=784×2
=1568(平方厘米)
答: 做一个这样的长方体礼盒至少需要1568平方厘米的包装材料。
根据题意,长方体的长=直径×3,长方体的高=10厘米,长方宽=直径×2,再根据长方体的表面积=(长×宽+长×高+宽×高)×2;据此解答。
