3.1.3 圆柱的体积(同步练习)(含答案)-2024-2025学年六年级数学下册(人教版)
文档属性
| 名称 | 3.1.3 圆柱的体积(同步练习)(含答案)-2024-2025学年六年级数学下册(人教版) |
|
|
| 格式 | docx | ||
| 文件大小 | 291.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 15:26:15 | ||
图片预览



文档简介
3.3 圆柱的体积(同步练习)
一、单选题
1.一个圆柱容器底面积是高20cm,原来水面高度是8cm,往容器内浸没物体后,水面高度均上升至10cm,下面说法错误的是( )。
A.正方体、圆锥、圆柱的体积相同
B.圆锥的体积是
C.圆锥的高度是圆柱的3倍
D.三个物体全部浸入一个容器,水不会溢出
2.如下图2,将长方形 ABCD 分别沿长和宽所在的直线旋转一周,得到圆柱(1)和圆柱 (2)。这两个圆柱相比较, ( )。
A.表面积和体积都相等 B.表面积相等,体积不相等
C.表面积不相等,体积相等 D.表面积和体积都不相等
3.小明买了一瓶水喝掉了一部分后还有剩余(如图所示),已知这个饮料瓶的内直径是6cm。根据如图中标出的数据,小明用算式“3.14×(6÷2)2×(18+7)”计算的是( )
A.喝掉的水的体积。
B.瓶子的容积。
C.剩余水的体积。
D.喝掉的水和剩余的水相差的体积。
4.如下图,三个杯子中的饮料相比较,( )。(单位:厘米)
A.甲最多 B.乙最多 C.丙最多 D.一样多
5. 一个圆柱形物体的底面积约是30cm2,高是 13cm,这个物体可能是( )。
A.一支铅笔 B.一个易拉罐
C.一个水桶 D.一台体重电子秤
二、填空题
6.如图,将圆锥形酒杯装满酒,再倒入空圆柱形容器中,至少要倒 次才能倒满圆柱形容器。(酒杯和容器的厚度忽略不计)
7.如图,一根长9分米的圆柱形木料,平均锯成3段,表面积增加了12.56平方分米,那么原来木料的体积是 立方分米。
8.圆柱的底面半径和高都扩大到原来的2倍,则它的底面积扩大到原来的 倍,体积扩大到原来的 倍。
9.从正面观察一个圆柱,看到的形状是一个边长是20厘米的正方形,这个圆柱的表面积是 平方厘米,体积是 立方厘米。
10.把棱长6cm的正方体木块削成一个最大的圆柱,圆柱的体积是 cm3。若再把这个圆柱削成一个最大的圆锥,这个圆锥的体积是 cm3。
三、解决问题
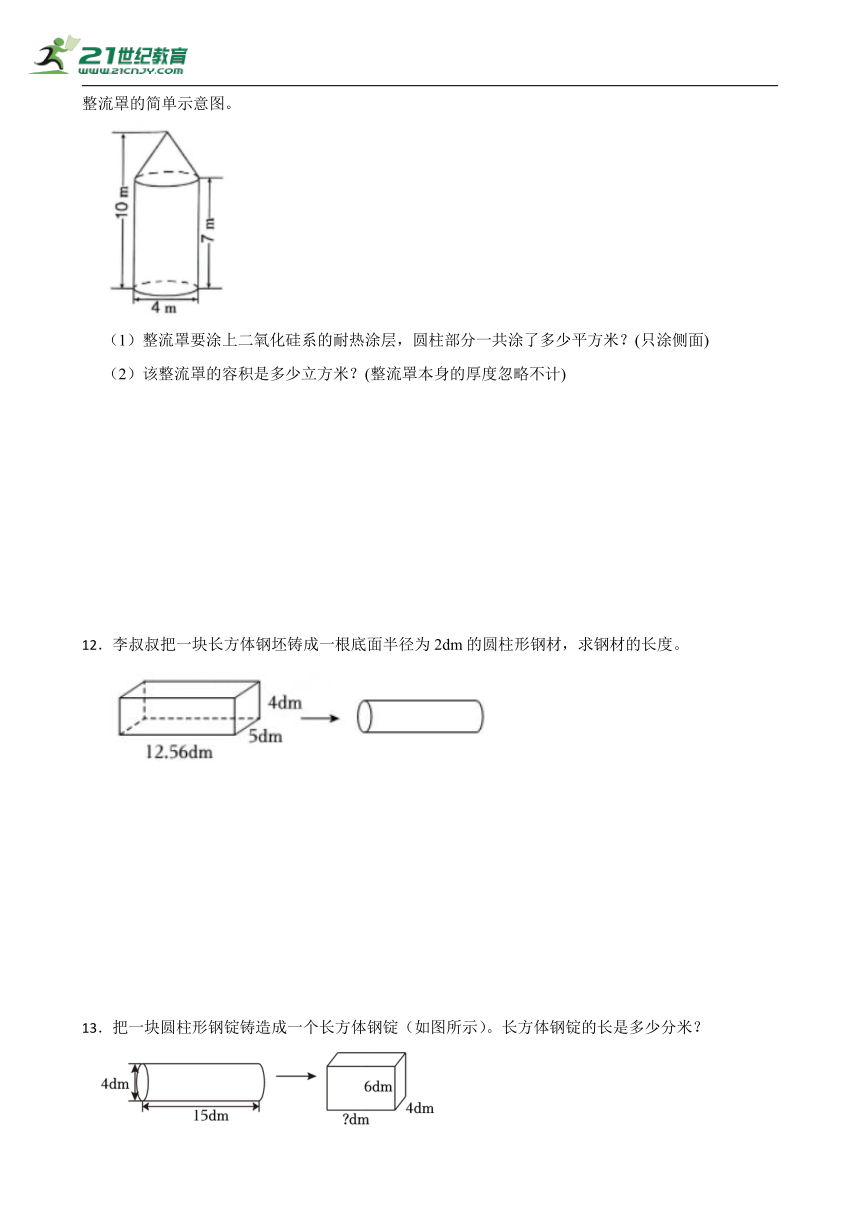
11.整流罩是运载火箭的重要组成部分,外形通常由近似的圆柱和圆锥组成。下边是某型号运载火箭整流罩的简单示意图。
(1)整流罩要涂上二氧化硅系的耐热涂层,圆柱部分一共涂了多少平方米?(只涂侧面)
(2)该整流罩的容积是多少立方米?(整流罩本身的厚度忽略不计)
12.李叔叔把一块长方体钢坯铸成一根底面半径为2dm的圆柱形钢材,求钢材的长度。
13.把一块圆柱形钢锭铸造成一个长方体钢锭(如图所示)。长方体钢锭的长是多少分米?
14.如下图,一个底面半径为6分米的无水圆柱体鱼缸,里面放着一块体积为12.56立方分米,底面直径为4分米的圆锥体假山石。如果水管以每分钟16立方分米的流量向里面注水,至少需要多少分钟才能将假山石完全淹没?(结果保留整数)
15.在一个底面半径是 20cm的圆柱形容器里盛有一些水,现放入一个底面直径是 20cm的金属圆锥,圆锥浸没在水中,水面上升了5cm 且未溢出。这个圆锥的高是多少厘米
答案解析部分
1.C
解:A:水面都是升高了2厘米,说明正方体、圆锥、圆柱的体积相同 ,原题说法正确;
B:240×(10-8)=480(立方厘米),圆锥的体积是,原题说法正确;
C:不知道圆柱圆锥的底面积,不能判断圆锥的高度是不是圆柱的3倍 ,原题说法错误;
D:2+2+2+8=14(厘米),14厘米<20厘米,三个物体全部浸入一个容器,水不会溢出 ,原题说法正确。
故答案为:C。
圆柱容器底面积×水面上升的高度=浸没物体的体积。
2.D
解:(1)表面积:
3.14×32×2+3.14×3×2×6
=3.14×18+3.14×36
=3.14×54
体积:3.14×32×6=3.14×54;
(2)表面积:
3.14×62×2+3.14×6×2×3
=3.14×72+3.14×36
=3.14×108
体积:3.14×62×3=3.14×108‘
所以两个圆柱的表面积和体积都不相等。
故答案为:D。’
以6厘米的边为轴旋转得到的圆柱的高是6厘米,底面半径是3厘米;以3厘米的边为轴旋转得到的圆柱底面半径是6厘米,高是3厘米。分别计算出表面积和体积再比较即可。
3.B
解:“(6÷2)”是饮料瓶的内半径,“(18+7)”是喝掉水加剩下水的高度和,所以“3.14×(6÷2)2×(18+7)”计算的是饮料瓶的容积。
故答案为:B。
右边高度为18cm的圆柱的体积为喝掉水的体积,左边高度为7cm的圆柱的体积为剩下水的体积,两个的体积之和就是圆柱的容积。
4.A
解:甲:π×(8÷2)2×4=64π;
乙:π×(6÷2)2×4=36π;
丙:π×(5÷2)2×4=25π;
64π>36π>25π,则甲最多。
故答案为:A。
饮料的体积=容器的底面积×高,其中,底面积=π×半径2,然后比较大小。
5.B
解:一个物体的底面积约是30平方厘米,高是13厘米的问题最有可能是一个易拉罐。
故答案为:B。
根据生活经验可知,一个物体的底面积约是30平方厘米,高是13厘米的问题最有可能是一个易拉罐。据此解答即可。
6.6
解:圆柱的容积:
π×(10÷2)2×12
=π×52×12
=π×25×12
=300π(立方厘米),
圆锥的容积:
π×(10-2)2×6÷3
=π×52×6÷3
=π×25×6÷3
=150π÷3
=50π(立方厘米),
300π÷50π=6(次);
故答案为:6。
圆锥的体积:V=πr2h÷3,据此求出圆锥形容器的容积,即水的体积,圆柱的体积:V=πr2h,据此求出圆柱形容器的容积,用圆柱形容器的容积除以圆锥形酒杯的容积,就是需要倒满的次数。
7.28.26
解:12.56÷4=3.14(平方分米)
3.14×9=28.26(立方分米)
故答案为:28.26。
增加的表面积÷4=圆柱的底面积,圆柱的底面积×高=圆柱的体积。
8.4;8
解:假设圆柱的底面半径和高都为1,则扩大后都为2,扩大后的底面积为:,扩大后的体积为:。
故答案为:4;8。
圆的面积=π×半径2;圆柱的体积=π×半径2×高。
9.1874;6280
解:表面积:3.14×(20÷2)2×2+3.14×20×20
=3.14×100×2+1256
=618+1256
=1874(平方厘米);
体积:3.14×(20÷2)2×20
=3.14×100×20
=6280(立方厘米);
故答案为:1874;6280。
由题意可知,这个圆柱的底面直径与高都是20厘米,根据圆柱表面积=底面积×2+侧面积,侧面积=底面周长×高,体积=底面积×高,代入数值计算即可。
10.169.56;56.52
解:圆柱的体积:3.14×(6÷2)2×6
=3.14×9×6
=28.26×6
=169.56(cm3);
圆锥的体积:169.56×=56.52(cm3);
故答案为:169.56;56.52。
削成的最大的圆柱的直径和高都等于正方体的棱长,根据圆柱体积=π×半径2×高,代入数值计算即可;削成的最大的圆锥与圆柱等底等高,因此,圆锥的体积是圆柱体积的,用圆柱的体积乘即可求出圆锥的体积。
11.(1)解:3.14×4×7
=12.56×7
=87.92(平方米)
答:圆柱部分一共涂了87.92平方米。
(2)解:3.14×()2×7+×3.14×()2×(10-7)
=87.92+12.56
=100.48(m3)
答:该整流罩的容积是100.48m3。
(1)圆柱部分一共涂的面积=侧面积=π×直径×高;
(2)该整流罩的容积=圆柱的容积+圆锥的容积;其中,圆柱的容积=π×半径2×高,圆锥的容积=π×半径2×高÷3。
12.解:12.56×5×4÷(3.14×22)
=251.2÷12.56
=20(dm)
答:钢材的长度是20dm。
熔铸前后钢材的体积不变,用长方体的体积除以圆柱的底面积即可求出钢材的长度。长方体体积=长×宽×高,圆柱的体积=底面积×高。
13.解:4÷2=2(分米)
2×2×3.14×15
=12.56×15
=188.4(立方分米)
188.4÷6÷4
=31.4÷4
=7.85(分米)
答:长方体钢锭的长是7.85分米。
本题属于等积变形,圆柱的体积=长方体的体积;π×底面半径的平方×高=圆柱的体积,圆柱的体积÷长方体的高÷长方体的宽=长方体的长。
14.解:4÷2=2(分米)
12.56×3÷(3.14×22)
=12.56×3÷12.56
=3(分米)
3.14×62×3-12.56
=339.12-12.56
=326.56(立方分米)
326.56÷16≈21(分钟)
答:至少需要21分钟才能将假山石完全淹没。
将假山石完全淹没至少需要的时间=将假山石完全淹没注入的水量÷平均每分钟的注水量,其中,将假山石完全淹没注入的水量=π×半径2×高-假山石的体积。
15.解:圆锥的体积:3.14×20×20×5=6280(立方厘米)
圆锥的底面半径:20÷2=10(厘米)
圆锥的底面积:3.14×10×10=314(平方厘米)
圆锥的高:6280×3÷314=60(厘米)
答:这个圆锥的高是60厘米。
圆柱的底面积×水面上升的高度=圆锥的体积,π×圆锥的底面半径的平方=圆锥的底面积,圆锥的体积×3÷圆锥的底面积=这个圆锥的高。
一、单选题
1.一个圆柱容器底面积是高20cm,原来水面高度是8cm,往容器内浸没物体后,水面高度均上升至10cm,下面说法错误的是( )。
A.正方体、圆锥、圆柱的体积相同
B.圆锥的体积是
C.圆锥的高度是圆柱的3倍
D.三个物体全部浸入一个容器,水不会溢出
2.如下图2,将长方形 ABCD 分别沿长和宽所在的直线旋转一周,得到圆柱(1)和圆柱 (2)。这两个圆柱相比较, ( )。
A.表面积和体积都相等 B.表面积相等,体积不相等
C.表面积不相等,体积相等 D.表面积和体积都不相等
3.小明买了一瓶水喝掉了一部分后还有剩余(如图所示),已知这个饮料瓶的内直径是6cm。根据如图中标出的数据,小明用算式“3.14×(6÷2)2×(18+7)”计算的是( )
A.喝掉的水的体积。
B.瓶子的容积。
C.剩余水的体积。
D.喝掉的水和剩余的水相差的体积。
4.如下图,三个杯子中的饮料相比较,( )。(单位:厘米)
A.甲最多 B.乙最多 C.丙最多 D.一样多
5. 一个圆柱形物体的底面积约是30cm2,高是 13cm,这个物体可能是( )。
A.一支铅笔 B.一个易拉罐
C.一个水桶 D.一台体重电子秤
二、填空题
6.如图,将圆锥形酒杯装满酒,再倒入空圆柱形容器中,至少要倒 次才能倒满圆柱形容器。(酒杯和容器的厚度忽略不计)
7.如图,一根长9分米的圆柱形木料,平均锯成3段,表面积增加了12.56平方分米,那么原来木料的体积是 立方分米。
8.圆柱的底面半径和高都扩大到原来的2倍,则它的底面积扩大到原来的 倍,体积扩大到原来的 倍。
9.从正面观察一个圆柱,看到的形状是一个边长是20厘米的正方形,这个圆柱的表面积是 平方厘米,体积是 立方厘米。
10.把棱长6cm的正方体木块削成一个最大的圆柱,圆柱的体积是 cm3。若再把这个圆柱削成一个最大的圆锥,这个圆锥的体积是 cm3。
三、解决问题
11.整流罩是运载火箭的重要组成部分,外形通常由近似的圆柱和圆锥组成。下边是某型号运载火箭整流罩的简单示意图。
(1)整流罩要涂上二氧化硅系的耐热涂层,圆柱部分一共涂了多少平方米?(只涂侧面)
(2)该整流罩的容积是多少立方米?(整流罩本身的厚度忽略不计)
12.李叔叔把一块长方体钢坯铸成一根底面半径为2dm的圆柱形钢材,求钢材的长度。
13.把一块圆柱形钢锭铸造成一个长方体钢锭(如图所示)。长方体钢锭的长是多少分米?
14.如下图,一个底面半径为6分米的无水圆柱体鱼缸,里面放着一块体积为12.56立方分米,底面直径为4分米的圆锥体假山石。如果水管以每分钟16立方分米的流量向里面注水,至少需要多少分钟才能将假山石完全淹没?(结果保留整数)
15.在一个底面半径是 20cm的圆柱形容器里盛有一些水,现放入一个底面直径是 20cm的金属圆锥,圆锥浸没在水中,水面上升了5cm 且未溢出。这个圆锥的高是多少厘米
答案解析部分
1.C
解:A:水面都是升高了2厘米,说明正方体、圆锥、圆柱的体积相同 ,原题说法正确;
B:240×(10-8)=480(立方厘米),圆锥的体积是,原题说法正确;
C:不知道圆柱圆锥的底面积,不能判断圆锥的高度是不是圆柱的3倍 ,原题说法错误;
D:2+2+2+8=14(厘米),14厘米<20厘米,三个物体全部浸入一个容器,水不会溢出 ,原题说法正确。
故答案为:C。
圆柱容器底面积×水面上升的高度=浸没物体的体积。
2.D
解:(1)表面积:
3.14×32×2+3.14×3×2×6
=3.14×18+3.14×36
=3.14×54
体积:3.14×32×6=3.14×54;
(2)表面积:
3.14×62×2+3.14×6×2×3
=3.14×72+3.14×36
=3.14×108
体积:3.14×62×3=3.14×108‘
所以两个圆柱的表面积和体积都不相等。
故答案为:D。’
以6厘米的边为轴旋转得到的圆柱的高是6厘米,底面半径是3厘米;以3厘米的边为轴旋转得到的圆柱底面半径是6厘米,高是3厘米。分别计算出表面积和体积再比较即可。
3.B
解:“(6÷2)”是饮料瓶的内半径,“(18+7)”是喝掉水加剩下水的高度和,所以“3.14×(6÷2)2×(18+7)”计算的是饮料瓶的容积。
故答案为:B。
右边高度为18cm的圆柱的体积为喝掉水的体积,左边高度为7cm的圆柱的体积为剩下水的体积,两个的体积之和就是圆柱的容积。
4.A
解:甲:π×(8÷2)2×4=64π;
乙:π×(6÷2)2×4=36π;
丙:π×(5÷2)2×4=25π;
64π>36π>25π,则甲最多。
故答案为:A。
饮料的体积=容器的底面积×高,其中,底面积=π×半径2,然后比较大小。
5.B
解:一个物体的底面积约是30平方厘米,高是13厘米的问题最有可能是一个易拉罐。
故答案为:B。
根据生活经验可知,一个物体的底面积约是30平方厘米,高是13厘米的问题最有可能是一个易拉罐。据此解答即可。
6.6
解:圆柱的容积:
π×(10÷2)2×12
=π×52×12
=π×25×12
=300π(立方厘米),
圆锥的容积:
π×(10-2)2×6÷3
=π×52×6÷3
=π×25×6÷3
=150π÷3
=50π(立方厘米),
300π÷50π=6(次);
故答案为:6。
圆锥的体积:V=πr2h÷3,据此求出圆锥形容器的容积,即水的体积,圆柱的体积:V=πr2h,据此求出圆柱形容器的容积,用圆柱形容器的容积除以圆锥形酒杯的容积,就是需要倒满的次数。
7.28.26
解:12.56÷4=3.14(平方分米)
3.14×9=28.26(立方分米)
故答案为:28.26。
增加的表面积÷4=圆柱的底面积,圆柱的底面积×高=圆柱的体积。
8.4;8
解:假设圆柱的底面半径和高都为1,则扩大后都为2,扩大后的底面积为:,扩大后的体积为:。
故答案为:4;8。
圆的面积=π×半径2;圆柱的体积=π×半径2×高。
9.1874;6280
解:表面积:3.14×(20÷2)2×2+3.14×20×20
=3.14×100×2+1256
=618+1256
=1874(平方厘米);
体积:3.14×(20÷2)2×20
=3.14×100×20
=6280(立方厘米);
故答案为:1874;6280。
由题意可知,这个圆柱的底面直径与高都是20厘米,根据圆柱表面积=底面积×2+侧面积,侧面积=底面周长×高,体积=底面积×高,代入数值计算即可。
10.169.56;56.52
解:圆柱的体积:3.14×(6÷2)2×6
=3.14×9×6
=28.26×6
=169.56(cm3);
圆锥的体积:169.56×=56.52(cm3);
故答案为:169.56;56.52。
削成的最大的圆柱的直径和高都等于正方体的棱长,根据圆柱体积=π×半径2×高,代入数值计算即可;削成的最大的圆锥与圆柱等底等高,因此,圆锥的体积是圆柱体积的,用圆柱的体积乘即可求出圆锥的体积。
11.(1)解:3.14×4×7
=12.56×7
=87.92(平方米)
答:圆柱部分一共涂了87.92平方米。
(2)解:3.14×()2×7+×3.14×()2×(10-7)
=87.92+12.56
=100.48(m3)
答:该整流罩的容积是100.48m3。
(1)圆柱部分一共涂的面积=侧面积=π×直径×高;
(2)该整流罩的容积=圆柱的容积+圆锥的容积;其中,圆柱的容积=π×半径2×高,圆锥的容积=π×半径2×高÷3。
12.解:12.56×5×4÷(3.14×22)
=251.2÷12.56
=20(dm)
答:钢材的长度是20dm。
熔铸前后钢材的体积不变,用长方体的体积除以圆柱的底面积即可求出钢材的长度。长方体体积=长×宽×高,圆柱的体积=底面积×高。
13.解:4÷2=2(分米)
2×2×3.14×15
=12.56×15
=188.4(立方分米)
188.4÷6÷4
=31.4÷4
=7.85(分米)
答:长方体钢锭的长是7.85分米。
本题属于等积变形,圆柱的体积=长方体的体积;π×底面半径的平方×高=圆柱的体积,圆柱的体积÷长方体的高÷长方体的宽=长方体的长。
14.解:4÷2=2(分米)
12.56×3÷(3.14×22)
=12.56×3÷12.56
=3(分米)
3.14×62×3-12.56
=339.12-12.56
=326.56(立方分米)
326.56÷16≈21(分钟)
答:至少需要21分钟才能将假山石完全淹没。
将假山石完全淹没至少需要的时间=将假山石完全淹没注入的水量÷平均每分钟的注水量,其中,将假山石完全淹没注入的水量=π×半径2×高-假山石的体积。
15.解:圆锥的体积:3.14×20×20×5=6280(立方厘米)
圆锥的底面半径:20÷2=10(厘米)
圆锥的底面积:3.14×10×10=314(平方厘米)
圆锥的高:6280×3÷314=60(厘米)
答:这个圆锥的高是60厘米。
圆柱的底面积×水面上升的高度=圆锥的体积,π×圆锥的底面半径的平方=圆锥的底面积,圆锥的体积×3÷圆锥的底面积=这个圆锥的高。
