3.2.1 圆锥的认识(同步练习)-2024-2025学年六年级数学下册(人教版)(含答案)
文档属性
| 名称 | 3.2.1 圆锥的认识(同步练习)-2024-2025学年六年级数学下册(人教版)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 356.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 15:25:53 | ||
图片预览


文档简介
3.2.1 圆锥的认识(同步练习)
一、单选题
1.下面四种测量圆锥高的方法中,你认为( )正确。
A. B.
C. D.
2.在下图中,以直线为轴旋转一周,可以得到圆锥的是( )。
A. B. C. D.
3.如下图是等底等高的圆锥和圆柱,从不同方向会看到不同的形状,从右边看到的图形是( )
A. B. C. D.
4.小军用下图的方法测量一个圆锥的高,量出长度是6厘米,圆锥实际的高( )。
A.小于6厘米 B.大于6厘米 C.等于6厘米 D.不能确定
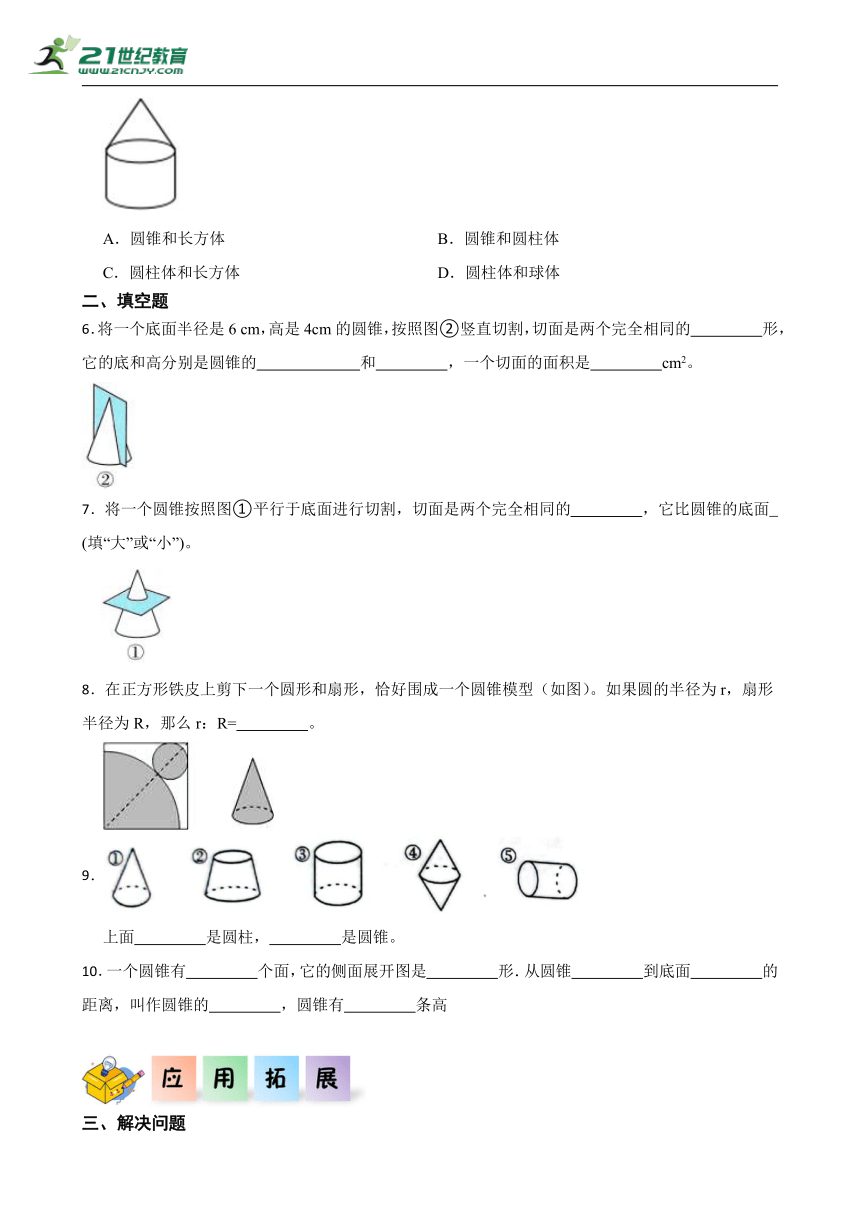
5.下面的图形是由什么组合而成( )。
A.圆锥和长方体 B.圆锥和圆柱体
C.圆柱体和长方体 D.圆柱体和球体
二、填空题
6.将一个底面半径是6 cm,高是4cm的圆锥,按照图②竖直切割,切面是两个完全相同的 形,它的底和高分别是圆锥的 和 ,一个切面的面积是 cm2。
7.将一个圆锥按照图①平行于底面进行切割,切面是两个完全相同的 ,它比圆锥的底面 (填“大”或“小”)。
8.在正方形铁皮上剪下一个圆形和扇形,恰好围成一个圆锥模型(如图)。如果圆的半径为r,扇形半径为R,那么r:R= 。
9.
上面 是圆柱, 是圆锥。
10.一个圆锥有 个面,它的侧面展开图是 形.从圆锥 到底面 的距离,叫作圆锥的 ,圆锥有 条高
三、解决问题
11.如图,一个底面周长为28.26 cm、高为10 cm的圆锥,过顶点沿底面直径纵向切成两半,这个圆锥的表面积增加了多少?
12.如图,把一个半径为8cm、圆心角是270°的扇形卷成一个圆锥,这个圆锥的底面积是多少平方厘米?
13.一个圆锥的底面周长是15.7厘米,高是3厘米.从圆锥的顶点沿着高将它切成两半后,表面积之和比原圆锥的表面积增加了多少平方厘米?
14.有一个圆锥见下图,AB和BC长均为10cm,底面积周长为10π厘米,有一只小虫准备从A点出发,沿着锥面爬到线段BC上,那么,它爬行的最短距离是多少厘米?
15.你知道怎样求圆锥的侧面积吗?
答案解析部分
1.C
解:A、B两个图形测量的不是圆锥的顶点到底面圆心的距离,方法不正确;
C图形测量的是圆锥的顶点到底面圆心的距离,方法是正确的。
D图形不能从直尺的顶端开始测量,要从0刻度开始测量,方法不正确。
故答案为:C。
从圆锥的顶点到底面圆心的距离是圆锥的高;据此解答。
2.C
解:直角三角形沿着其中一条直角边旋转一周,得到一个圆锥。
故答案为:C。
直角三角形的有两条直角边,依据圆锥的特点,直角三角形沿着其中一条直角边旋转一周,得到一个圆锥。
3.D
解:从右边看到的图形是:。
故答案为:D。
根据题意,立体图形从右边看:圆柱在前,圆柱遮挡圆锥,圆柱的侧面是长方形。
4.A
解:圆锥实际的高小于6厘米。
故答案为:A。
从圆锥的顶点到底面圆心的距离,叫做圆锥的高,如图测量方法,圆锥实际的高小于6厘米。
5.B
解: 是由圆锥和圆柱组合而成的。
故答案为:B。
圆锥的特征:侧面展开是一个扇形,只有下底为圆,从侧面水平看是一个等腰三角形。
圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。它有2个大小相同、相互平行的圆形底面和1个曲面侧面。其侧面展开是矩形。
本题据此进行解答。
6.三角;底面直径;高;24
解:按照图②竖直切割,切面是两个完全相同的三角形,它的底和高分别是圆锥的底面直径和高,
6×2×4÷2=24(厘米)。
故答案为:三角;底面直径;高;24。
一个切面的面积=圆锥的底面直径×圆锥的高÷2。
7.圆;小
解:切面是两个完全相同的圆,它比圆锥的底面小。
故答案为:圆;小。
平行于底面切割圆锥,越向下切面的面积越大。
8.1:4
解:2πr=2πR×
r=R
r:R=1:4
故答案为:1:4。
圆的周长=扇形的弧长,就此解答即可。
9.③、⑤;①
解:③、⑤是圆柱;①是圆锥。
故答案为:③、⑤;①。
像③、⑤一样直直的、上下一样粗细、能滚动的物体,在数学上叫做圆柱;像①一样由一个圆和一个曲面组成的立体图形是圆锥。
10.2;扇;顶点;圆心;高;1
解:一个圆锥有2个面,它的侧面展开图是扇形.从圆锥顶点到底面圆心的距离,叫作圆锥的高,圆锥有1条高。
故答案为:2;扇;顶点;圆心;高;1。
圆锥的的两个面为底面和侧面。圆锥体积=π×半径的平方×高÷3。
11.解:底面直径:28.26÷3.14=9(厘米)
增加的表面积:9×10÷2 ×2 =90( 平方厘米 )
答:这个圆锥的表面积增加了90平方厘米。
将圆锥过顶点沿底面直径纵向切成两半后,表面积比原来的圆锥的表面积增加了2个以圆锥的底面直径为底,以圆锥的高为高的三角形的面积。底面周长÷π=底面直径,底面直径×圆锥的高÷2=1个三角形的面积,1个三角形的面积×2=这个圆锥增加的表面积。
12.解:3.14×2×8×÷3.14÷2
=50.24×÷3.14÷2
=37.68÷3.14÷2
=6(cm)
3.14×6×6=113.04(cm2)
答:这个圆锥的底面积是113.04平方厘米。
π×2×底面半径=圆的周长,圆的周长×=圆锥的底面周长,圆锥的底面周长÷π÷2=圆锥的底面半径,π×底面半径的平方=圆锥的底面积。
13.解:圆锥的底面直径为:15.7÷3.14=5(厘米)
则切割后表面积增加了:5×3÷2×2=15(平方厘米)
答:表面积之和比原来圆锥表面积增加15平方厘米。
切成两半后,表面积增加了2个三角形面积;
底面周长÷π=底面直径,底面直径就是三角形的底;
三角形的底×三角形的高÷2=一个三角形面积,一个三角形面积×2=增加的面积。
14.解:小虫从A点出发,沿AB爬行到BC上,所以小虫爬行的最短距离为10cm.
小虫直接沿着AB爬行,这样爬到BC上的距离就是最短的距离,也就是10cm.
15.解:如图中圆锥的底面半径是r,图中线段AB的长设为l(AB这条线段也叫做圆锥的母线).将圆锥展开后会得到一个扇形,这个扇形的半径就是l,那么这个扇形的圆心角是多少度呢?
我们可以这样来计算扇形圆心角的度数: ,那么扇形的面积应为: ,这也就是求圆锥侧面积的公式.
圆锥的侧面积展开后是一个扇形,要想计算扇形的面积,就要确定扇形的圆心角度数和半径的长度,根据图中数据计算即可.
一、单选题
1.下面四种测量圆锥高的方法中,你认为( )正确。
A. B.
C. D.
2.在下图中,以直线为轴旋转一周,可以得到圆锥的是( )。
A. B. C. D.
3.如下图是等底等高的圆锥和圆柱,从不同方向会看到不同的形状,从右边看到的图形是( )
A. B. C. D.
4.小军用下图的方法测量一个圆锥的高,量出长度是6厘米,圆锥实际的高( )。
A.小于6厘米 B.大于6厘米 C.等于6厘米 D.不能确定
5.下面的图形是由什么组合而成( )。
A.圆锥和长方体 B.圆锥和圆柱体
C.圆柱体和长方体 D.圆柱体和球体
二、填空题
6.将一个底面半径是6 cm,高是4cm的圆锥,按照图②竖直切割,切面是两个完全相同的 形,它的底和高分别是圆锥的 和 ,一个切面的面积是 cm2。
7.将一个圆锥按照图①平行于底面进行切割,切面是两个完全相同的 ,它比圆锥的底面 (填“大”或“小”)。
8.在正方形铁皮上剪下一个圆形和扇形,恰好围成一个圆锥模型(如图)。如果圆的半径为r,扇形半径为R,那么r:R= 。
9.
上面 是圆柱, 是圆锥。
10.一个圆锥有 个面,它的侧面展开图是 形.从圆锥 到底面 的距离,叫作圆锥的 ,圆锥有 条高
三、解决问题
11.如图,一个底面周长为28.26 cm、高为10 cm的圆锥,过顶点沿底面直径纵向切成两半,这个圆锥的表面积增加了多少?
12.如图,把一个半径为8cm、圆心角是270°的扇形卷成一个圆锥,这个圆锥的底面积是多少平方厘米?
13.一个圆锥的底面周长是15.7厘米,高是3厘米.从圆锥的顶点沿着高将它切成两半后,表面积之和比原圆锥的表面积增加了多少平方厘米?
14.有一个圆锥见下图,AB和BC长均为10cm,底面积周长为10π厘米,有一只小虫准备从A点出发,沿着锥面爬到线段BC上,那么,它爬行的最短距离是多少厘米?
15.你知道怎样求圆锥的侧面积吗?
答案解析部分
1.C
解:A、B两个图形测量的不是圆锥的顶点到底面圆心的距离,方法不正确;
C图形测量的是圆锥的顶点到底面圆心的距离,方法是正确的。
D图形不能从直尺的顶端开始测量,要从0刻度开始测量,方法不正确。
故答案为:C。
从圆锥的顶点到底面圆心的距离是圆锥的高;据此解答。
2.C
解:直角三角形沿着其中一条直角边旋转一周,得到一个圆锥。
故答案为:C。
直角三角形的有两条直角边,依据圆锥的特点,直角三角形沿着其中一条直角边旋转一周,得到一个圆锥。
3.D
解:从右边看到的图形是:。
故答案为:D。
根据题意,立体图形从右边看:圆柱在前,圆柱遮挡圆锥,圆柱的侧面是长方形。
4.A
解:圆锥实际的高小于6厘米。
故答案为:A。
从圆锥的顶点到底面圆心的距离,叫做圆锥的高,如图测量方法,圆锥实际的高小于6厘米。
5.B
解: 是由圆锥和圆柱组合而成的。
故答案为:B。
圆锥的特征:侧面展开是一个扇形,只有下底为圆,从侧面水平看是一个等腰三角形。
圆柱是由以矩形的一条边所在直线为旋转轴,其余三边绕该旋转轴旋转一周而形成的几何体。它有2个大小相同、相互平行的圆形底面和1个曲面侧面。其侧面展开是矩形。
本题据此进行解答。
6.三角;底面直径;高;24
解:按照图②竖直切割,切面是两个完全相同的三角形,它的底和高分别是圆锥的底面直径和高,
6×2×4÷2=24(厘米)。
故答案为:三角;底面直径;高;24。
一个切面的面积=圆锥的底面直径×圆锥的高÷2。
7.圆;小
解:切面是两个完全相同的圆,它比圆锥的底面小。
故答案为:圆;小。
平行于底面切割圆锥,越向下切面的面积越大。
8.1:4
解:2πr=2πR×
r=R
r:R=1:4
故答案为:1:4。
圆的周长=扇形的弧长,就此解答即可。
9.③、⑤;①
解:③、⑤是圆柱;①是圆锥。
故答案为:③、⑤;①。
像③、⑤一样直直的、上下一样粗细、能滚动的物体,在数学上叫做圆柱;像①一样由一个圆和一个曲面组成的立体图形是圆锥。
10.2;扇;顶点;圆心;高;1
解:一个圆锥有2个面,它的侧面展开图是扇形.从圆锥顶点到底面圆心的距离,叫作圆锥的高,圆锥有1条高。
故答案为:2;扇;顶点;圆心;高;1。
圆锥的的两个面为底面和侧面。圆锥体积=π×半径的平方×高÷3。
11.解:底面直径:28.26÷3.14=9(厘米)
增加的表面积:9×10÷2 ×2 =90( 平方厘米 )
答:这个圆锥的表面积增加了90平方厘米。
将圆锥过顶点沿底面直径纵向切成两半后,表面积比原来的圆锥的表面积增加了2个以圆锥的底面直径为底,以圆锥的高为高的三角形的面积。底面周长÷π=底面直径,底面直径×圆锥的高÷2=1个三角形的面积,1个三角形的面积×2=这个圆锥增加的表面积。
12.解:3.14×2×8×÷3.14÷2
=50.24×÷3.14÷2
=37.68÷3.14÷2
=6(cm)
3.14×6×6=113.04(cm2)
答:这个圆锥的底面积是113.04平方厘米。
π×2×底面半径=圆的周长,圆的周长×=圆锥的底面周长,圆锥的底面周长÷π÷2=圆锥的底面半径,π×底面半径的平方=圆锥的底面积。
13.解:圆锥的底面直径为:15.7÷3.14=5(厘米)
则切割后表面积增加了:5×3÷2×2=15(平方厘米)
答:表面积之和比原来圆锥表面积增加15平方厘米。
切成两半后,表面积增加了2个三角形面积;
底面周长÷π=底面直径,底面直径就是三角形的底;
三角形的底×三角形的高÷2=一个三角形面积,一个三角形面积×2=增加的面积。
14.解:小虫从A点出发,沿AB爬行到BC上,所以小虫爬行的最短距离为10cm.
小虫直接沿着AB爬行,这样爬到BC上的距离就是最短的距离,也就是10cm.
15.解:如图中圆锥的底面半径是r,图中线段AB的长设为l(AB这条线段也叫做圆锥的母线).将圆锥展开后会得到一个扇形,这个扇形的半径就是l,那么这个扇形的圆心角是多少度呢?
我们可以这样来计算扇形圆心角的度数: ,那么扇形的面积应为: ,这也就是求圆锥侧面积的公式.
圆锥的侧面积展开后是一个扇形,要想计算扇形的面积,就要确定扇形的圆心角度数和半径的长度,根据图中数据计算即可.
