华师大版(2024)数学七下6.1二元一次方程组和它的解 课件(共26张PPT)
文档属性
| 名称 | 华师大版(2024)数学七下6.1二元一次方程组和它的解 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-24 12:54:48 | ||
图片预览








文档简介
(共26张PPT)
(华师大版)七年级
下
6.1二元一次方程组和它的解
一次方程组
第6章
“六”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.理解二元一次方程、二元一次方程组和它的解的定义.
2.会检验一个数对是不是二元一次方程(组)的解.
3.能针对具体问题列出二元一次方程组.
新知导入
问题1:什么叫一元一次方程?
只含有一个未知数、左右两边都是整式,并且含未知数的项的次数都是1的方程叫做一元一次方程.
能使方程左、右两边的值相等的未知数的值,叫做方程的解.
将这个数分别代入原方程的左边和右边计算代数式的值,
如果左边右边,那么这个数就是这个方程的解;
如果左边右边,那么这个数就不是这个方程的解。
问题2:什么叫方程的解?
问题3:怎样检验一个数是不是这个方程的解?
暑假里,某地组织了“我们的小世界杯”足球邀请赛,
比赛规定:胜一场得3分,平一场得1分,负一场得0分,
勇士队在第一轮比赛中赛了9场,负了2场,共得17分。
那么这个队胜了几场?平了几场呢?
你会解决这个问题吗?
新知讲解
问题1:
思考:
新知讲解
问题1中告诉了我们哪些等量关系 问题1中有两个未知数,如果分别设为x、y,又会怎样呢
等量关系:①胜的场数+平的场数+负的场数=比赛总场数;
②胜场得分+平场得分=比赛总得分.
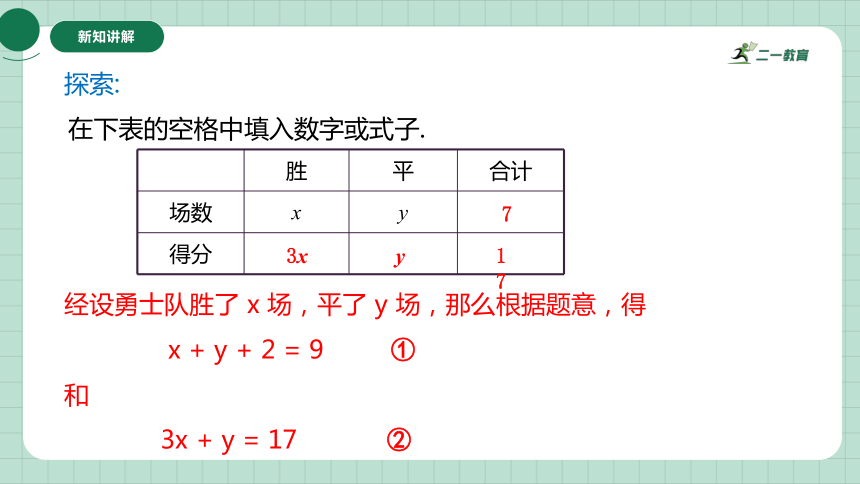
探索:
新知讲解
在下表的空格中填入数字或式子.
胜 平 合计
场数 x y
得分
7
3x
y
17
经设勇士队胜了 x 场,平了 y 场,那么根据题意,得
x + y + 2 = 9 ①
和
3x + y = 17 ②
新知讲解
观察这两个方程有什么共同特点?
x + y = 9-2 ①
3x + y = 17 ②
①每个方程都有两个未知数;
②未知数项的次数都是1;
③含有未知数的式子都是整式.
新知讲解
概括:
x + y = 9-2 ①
3x + y = 17 ②
像这样,有两个未知数,并且含有未知数的项的次数都是1的方程,叫做二元一次方程.
二元一次方程必须满足的特点:
1. 是整式方程;
2. 只含有两个未知数,且未知数的系数不为 0;
3. “一次”是指含未知数的项的次数是 1, 而不是未知数的次数.
这个问题中,两个未知量(比赛场数)要满足两个等量关系.相应地,两个未知数x、y必须同时满足①②两个方程.因此,把这两个方程合在一起,并写成
新知讲解
像这样,两个二元一次方程合在一起,就组成了一个二元一次方程组.
新知讲解
二元一次方程组的特点:
①方程组有两个一次方程;
②方程组中共有2个不同的未知数;(方程组各方程中同一字母必须代表同一个量)
③用大括号把两个方程括起来.
新知讲解
用尝试检验、列算式或者通过列一元一次方程都可以求得勇士队胜了5场,平了2场,即x=5,y=2.
这里的x=5与y=2既满足方程①,即5+2=7;
又满足方程②,即3×5+2=17,
我们就说x=5与y=2是二元一次方程组的解,
并记作
新知讲解
一般地,使二元一次方程组中两个方程的左、右两边的值都相等的一对未知数的值,叫做二元一次方程组的解.
2.必须同时满足两个方程.
1.二元一次方程组的解是一对数,而不是两个数,必须用“ ”的形式;
注意
某校现有校舍20000m2,计划拆除部分旧校舍,改建新校舍,使校
舍总面积增加30%.若新建校舍的面积为被拆除的旧校舍面积的4倍,则应拆除多少旧校舍,建造多少新校舍
新知讲解
问题2:
若设应拆除x m2 旧校舍,建造y m2 新校舍,请你根据题意列出方程组.
新知讲解
试一试:
设应拆除 x m2 旧校舍,建造 y m2 新校舍.
y – x = 20 000×30%,
y = 4x.
【知识技能类作业】必做题:
课堂练习
1.有下列等式:① 2x-3y=4;② 5xy=8;③ y2-2x=0;④ -x=2.其中,是二元一次方程的有( )
A. 1个 B. 2个 C. 3个 D. 4个
A
【知识技能类作业】必做题:
课堂练习
2.解为的方程组可以是( )
A. B.
C. D.
C
3.某市举办中学生足球赛,按比赛规则,每场比赛都要分出胜负,胜1场得3分,负1场扣1分,菁英中学队在8场比赛中得到12分,若设该队胜的场数为,负的场数为 ,则可列方程组为( )
A. B.
C. D.
【知识技能类作业】必做题:
课堂练习
C
【知识技能类作业】选做题:
课堂练习
4.若是二元一次方程组的解,则 ___.
9
5.已知方程组的解为由于不小心滴上了两滴墨水,刚好遮住了两个数●和★,求●和★的值.
【知识技能类作业】选做题:
课堂练习
解:由题意,把x=5代入2x-y=12,
得2×5-y=12,解得y=-2.
∴ 2x+y=2×5-2=8.
∴ ●是8,★是-2
【综合拓展类作业】
课堂练习
6. 某工厂三个车间共有180人,第二个车间的人数比第一个车间人数的3倍多1,第三个车间的人数比第一个车间人数的少1,问:三个车间各有多少人
(1) 用一元一次方程解题;
解:(1) 设第一个车间有x人,则第二个车间有(3x+1)人,第三个车间有人.
根据题意,得x+(3x+1)+=180,解得x=40.经检验,符合题意.
∴ 3x+1=121,x-1=19.
∴ 第一个车间有40人,第二个车间有121人,第三个车间有19人。
【综合拓展类作业】
课堂练习
(2) 设两个未知数,并且根据条件,列出含有两个未知数的方程组(不必求解).
解:(2) 答案不唯一,如设第一个车间有x人,第二个车间有y人,则第三个车间有人.
根据题意,得
课堂总结
1.二元一次方程:
有两个未知数,并且含有未知数的项的次数都是1的方程,叫做二元一次方程.
2.二元一次方程组:
两个二元一次方程合在一起,就组成了一个二元一次方程组.
3.二元一次方程组的解:
一般地,使二元一次方程组中两个方程的左、右两边的值都相等的一对未知数的值,叫做二元一次方程组的解.
板书设计
1.二元一次方程:
2.二元一次方程组:
3.二元一次方程组的解:
课题:6.1二元一次方程组和它的解
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(华师大版)七年级
下
6.1二元一次方程组和它的解
一次方程组
第6章
“六”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
板书设计
06
目录
07
内容总览
教学目标
1.理解二元一次方程、二元一次方程组和它的解的定义.
2.会检验一个数对是不是二元一次方程(组)的解.
3.能针对具体问题列出二元一次方程组.
新知导入
问题1:什么叫一元一次方程?
只含有一个未知数、左右两边都是整式,并且含未知数的项的次数都是1的方程叫做一元一次方程.
能使方程左、右两边的值相等的未知数的值,叫做方程的解.
将这个数分别代入原方程的左边和右边计算代数式的值,
如果左边右边,那么这个数就是这个方程的解;
如果左边右边,那么这个数就不是这个方程的解。
问题2:什么叫方程的解?
问题3:怎样检验一个数是不是这个方程的解?
暑假里,某地组织了“我们的小世界杯”足球邀请赛,
比赛规定:胜一场得3分,平一场得1分,负一场得0分,
勇士队在第一轮比赛中赛了9场,负了2场,共得17分。
那么这个队胜了几场?平了几场呢?
你会解决这个问题吗?
新知讲解
问题1:
思考:
新知讲解
问题1中告诉了我们哪些等量关系 问题1中有两个未知数,如果分别设为x、y,又会怎样呢
等量关系:①胜的场数+平的场数+负的场数=比赛总场数;
②胜场得分+平场得分=比赛总得分.
探索:
新知讲解
在下表的空格中填入数字或式子.
胜 平 合计
场数 x y
得分
7
3x
y
17
经设勇士队胜了 x 场,平了 y 场,那么根据题意,得
x + y + 2 = 9 ①
和
3x + y = 17 ②
新知讲解
观察这两个方程有什么共同特点?
x + y = 9-2 ①
3x + y = 17 ②
①每个方程都有两个未知数;
②未知数项的次数都是1;
③含有未知数的式子都是整式.
新知讲解
概括:
x + y = 9-2 ①
3x + y = 17 ②
像这样,有两个未知数,并且含有未知数的项的次数都是1的方程,叫做二元一次方程.
二元一次方程必须满足的特点:
1. 是整式方程;
2. 只含有两个未知数,且未知数的系数不为 0;
3. “一次”是指含未知数的项的次数是 1, 而不是未知数的次数.
这个问题中,两个未知量(比赛场数)要满足两个等量关系.相应地,两个未知数x、y必须同时满足①②两个方程.因此,把这两个方程合在一起,并写成
新知讲解
像这样,两个二元一次方程合在一起,就组成了一个二元一次方程组.
新知讲解
二元一次方程组的特点:
①方程组有两个一次方程;
②方程组中共有2个不同的未知数;(方程组各方程中同一字母必须代表同一个量)
③用大括号把两个方程括起来.
新知讲解
用尝试检验、列算式或者通过列一元一次方程都可以求得勇士队胜了5场,平了2场,即x=5,y=2.
这里的x=5与y=2既满足方程①,即5+2=7;
又满足方程②,即3×5+2=17,
我们就说x=5与y=2是二元一次方程组的解,
并记作
新知讲解
一般地,使二元一次方程组中两个方程的左、右两边的值都相等的一对未知数的值,叫做二元一次方程组的解.
2.必须同时满足两个方程.
1.二元一次方程组的解是一对数,而不是两个数,必须用“ ”的形式;
注意
某校现有校舍20000m2,计划拆除部分旧校舍,改建新校舍,使校
舍总面积增加30%.若新建校舍的面积为被拆除的旧校舍面积的4倍,则应拆除多少旧校舍,建造多少新校舍
新知讲解
问题2:
若设应拆除x m2 旧校舍,建造y m2 新校舍,请你根据题意列出方程组.
新知讲解
试一试:
设应拆除 x m2 旧校舍,建造 y m2 新校舍.
y – x = 20 000×30%,
y = 4x.
【知识技能类作业】必做题:
课堂练习
1.有下列等式:① 2x-3y=4;② 5xy=8;③ y2-2x=0;④ -x=2.其中,是二元一次方程的有( )
A. 1个 B. 2个 C. 3个 D. 4个
A
【知识技能类作业】必做题:
课堂练习
2.解为的方程组可以是( )
A. B.
C. D.
C
3.某市举办中学生足球赛,按比赛规则,每场比赛都要分出胜负,胜1场得3分,负1场扣1分,菁英中学队在8场比赛中得到12分,若设该队胜的场数为,负的场数为 ,则可列方程组为( )
A. B.
C. D.
【知识技能类作业】必做题:
课堂练习
C
【知识技能类作业】选做题:
课堂练习
4.若是二元一次方程组的解,则 ___.
9
5.已知方程组的解为由于不小心滴上了两滴墨水,刚好遮住了两个数●和★,求●和★的值.
【知识技能类作业】选做题:
课堂练习
解:由题意,把x=5代入2x-y=12,
得2×5-y=12,解得y=-2.
∴ 2x+y=2×5-2=8.
∴ ●是8,★是-2
【综合拓展类作业】
课堂练习
6. 某工厂三个车间共有180人,第二个车间的人数比第一个车间人数的3倍多1,第三个车间的人数比第一个车间人数的少1,问:三个车间各有多少人
(1) 用一元一次方程解题;
解:(1) 设第一个车间有x人,则第二个车间有(3x+1)人,第三个车间有人.
根据题意,得x+(3x+1)+=180,解得x=40.经检验,符合题意.
∴ 3x+1=121,x-1=19.
∴ 第一个车间有40人,第二个车间有121人,第三个车间有19人。
【综合拓展类作业】
课堂练习
(2) 设两个未知数,并且根据条件,列出含有两个未知数的方程组(不必求解).
解:(2) 答案不唯一,如设第一个车间有x人,第二个车间有y人,则第三个车间有人.
根据题意,得
课堂总结
1.二元一次方程:
有两个未知数,并且含有未知数的项的次数都是1的方程,叫做二元一次方程.
2.二元一次方程组:
两个二元一次方程合在一起,就组成了一个二元一次方程组.
3.二元一次方程组的解:
一般地,使二元一次方程组中两个方程的左、右两边的值都相等的一对未知数的值,叫做二元一次方程组的解.
板书设计
1.二元一次方程:
2.二元一次方程组:
3.二元一次方程组的解:
课题:6.1二元一次方程组和它的解
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
