北京市第三十五中学2024~2025学年初三下学期开学考数学试卷(无答案)
文档属性
| 名称 | 北京市第三十五中学2024~2025学年初三下学期开学考数学试卷(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 514.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-23 16:06:43 | ||
图片预览


文档简介
24-25第二学期 初三数学2月质量检测
一、单项选择题(下列各小题均有四个选项,其中只有一个选项符合题意. 共16分,每小题2分)
1.下列图形中,是轴对称图形但不是中心对称图形的是( ).
A. B. C. D.
2.在2025年春节档期,电影市场的热度持续高涨.电影《哪吒之魔童闹海》上映前三日,总票房便达到15.81亿元,这部电影在上映前三日平均每天的票房为( ).
A.元 B. 元 C. 元 D.元
3.实数在数轴上的对应点的位置如图所示,则正确的结论是( ).
A. B. C. D.
4.正六边形的每个内角度数为( ).
A.60° B.120° C. 135° D.150°
5.用配方法解一元二次方程,下列变形正确的是( ).
A. B. C. D.
6.如图,AB是⊙O的直径,C,D是⊙O上的两点.若∠CAB=65°,
则∠ADC的度数为( ).
A.65° B. 35° C.32.5° D.25°
7.把不等式组中两个不等式的解集在数轴上表示出来,正确的是( ).
A. B. C. D.
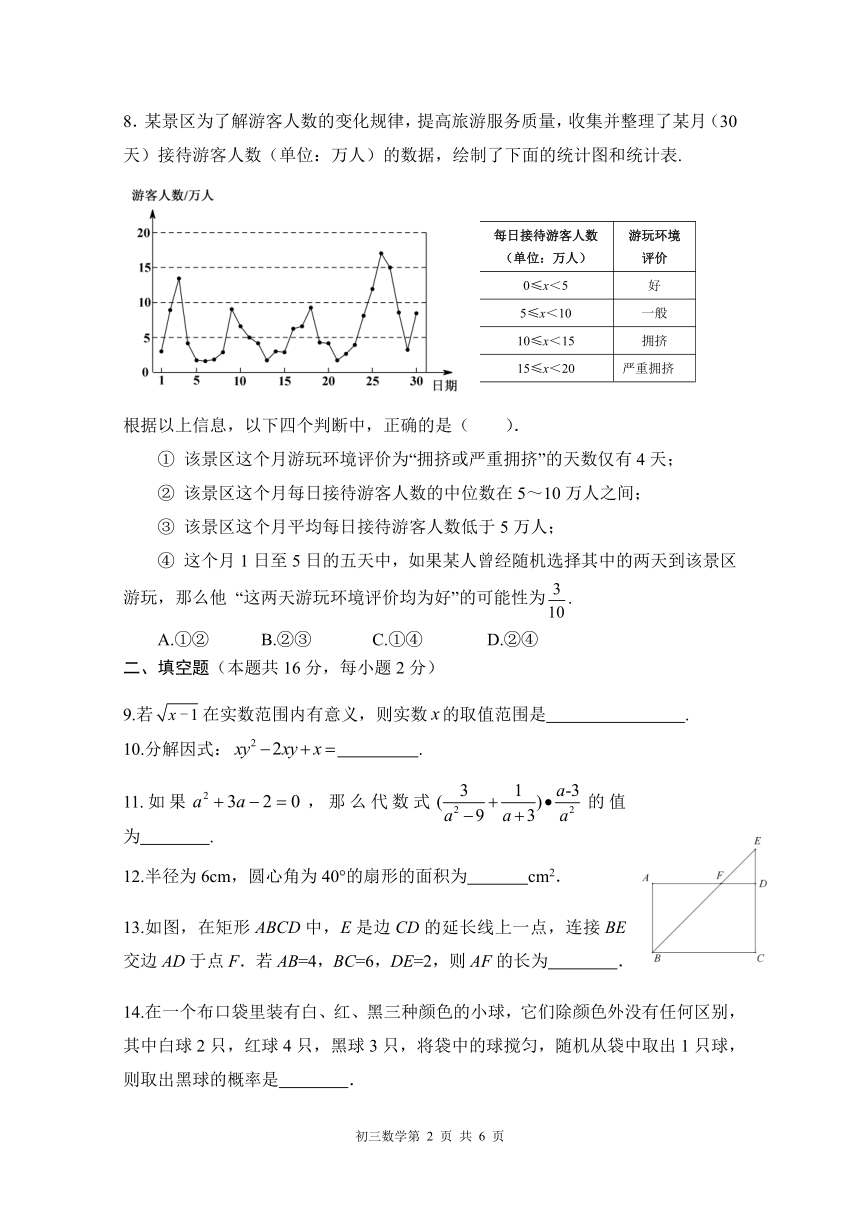
8.某景区为了解游客人数的变化规律,提高旅游服务质量,收集并整理了某月(30天)接待游客人数(单位:万人)的数据,绘制了下面的统计图和统计表.
根据以上信息,以下四个判断中,正确的是( ).
① 该景区这个月游玩环境评价为“拥挤或严重拥挤”的天数仅有4天;
② 该景区这个月每日接待游客人数的中位数在5~10万人之间;
③ 该景区这个月平均每日接待游客人数低于5万人;
④ 这个月1日至5日的五天中,如果某人曾经随机选择其中的两天到该景区游玩,那么他 “这两天游玩环境评价均为好”的可能性为.
A.①② B.②③ C.①④ D.②④
二、填空题(本题共16分,每小题2分)
9.若在实数范围内有意义,则实数的取值范围是 .
10.分解因式: .
11.如果,那么代数式的值为 .
12.半径为6cm,圆心角为40°的扇形的面积为 cm2.
13.如图,在矩形ABCD中,E是边CD的延长线上一点,连接BE交边AD于点F.若AB=4,BC=6,DE=2,则AF的长为 .
14.在一个布口袋里装有白、红、黑三种颜色的小球,它们除颜色外没有任何区别,其中白球2只,红球4只,黑球3只,将袋中的球搅匀,随机从袋中取出1只球,则取出黑球的概率是 .
15.《九章算术》中记载:“今有大器五、小器一容三斛;大器一、小器五容二斛.问大小器各容几何?”其大意是:今有大容器5个,小容器1个,总容量为3斛;大容器1个,小容器5个,总容量为2斛.问大容器、小容器的容量各是多少?设大容器容量为x斛,小容器容量为y斛,根据题意,可列方程组为 .(斛:古量器名,容量单位)
16. 某快递公司的快递件分为甲类件和乙类件,快递员送甲类件每件收入1元,送乙类件每件收入2元. 累计工作1小时,只送甲类件,最多可送30件,只送乙类件,最多可送10件;累计工作2小时,只送甲类件,最多可送55件,只送乙类件,最多可送20件;……,经整理形成统计表如下:
累计工作时长最多件数 (时)种类 (件) 1 2 3 4 5 6 7 8
甲类件 30 55 80 100 115 125 135 145
乙类件 10 20 30 40 50 60 70 80
(1)如果快递员一天工作8小时,且只送某一类件,那么他一天的最大收入为 元;
(2)如果快递员一天累计送x小时甲类件,y小时乙类件,且x+y=8,x,y均为正整数,那么他一天的最大收入为 元.
三、解答题(本题共68分,第17、18、19每题各5分;第20、21、22、24、25、26、27题,每题各6分;第23题4分;第28题7分)
17. 计算: .
18. 解不等式组:
19. 如图,在△ABC中,∠CAB=∠CBA,AD⊥BC于点D,BE⊥AC于点E.
求证:AD=BE.
20.关于x的一元二次方程有两个不相等的实数根.
(1)求n的取值范围;
(2)若n为取值范围内的最小整数,求此方程的根.
21.如图,在△ABC中,,D为AB边上一点,连接CD,E为CD中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.
(1)求证:四边形DBCF是平行四边形;
(2)若,,,求CD的长.
22. 下面是某同学设计的“作圆的内接正方形”的尺规作图的过程.
已知:如图1,⊙O.
求作:正方形ABCD,使正方形ABCD内接于⊙O.
作法:如图2,
① 过点O作直线AC,交⊙O于点A和C;
② 作线段AC的垂直平分线MN,交⊙O于点B和D;
③ 顺次连接AB,BC,CD和DA;
则正方形ABCD就是所求作的图形.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明: ∵ AC是⊙O的直径,
∴ ∠ABC =∠ADC = °,
又∵点B在线段AC的垂直平分线上,
∴ AB = BC,
∴ ∠BAC = ∠BCA = °.
同理 ∠DAC = 45°.
∴ ∠BAD = ∠BAC +∠DAC = 45° + 45° = 90°.
∴ ∠DAB = ∠ABC = ∠ADC = 90°,
∴ 四边形ABCD是矩形( )(填依据),
又∵ AB = BC,
∴ 四边形ABCD是正方形.
23. 进位制是人们为了记数和运算方便而约定的记数系统.约定逢三进一就是三进制,用数字0,1,2记数,三进制数可以转换为十进制数.例如,三进制数1212记为,由,可得是十进制数50.
(1)将转换为十进制数,结果是_______;
(2)对于一个用三进制表示的正整数,有下列两个结论:
①如果这个数的末位数字能被2整除,那么这个数就能被2整除;
②如果这个数的所有数位上的数字之和能被2整除,那么这个数就能被2整除.
从中选出正确结论,并以四位的三进制数为例,说明该结论正确的道理.
24.在平面直角坐标系xOy中,直线经过点A(1,m),B(,).
(1)求b和m的值;
(2)将点B向右平移到y轴上,得到点C,设点B关于原点的对称点为D,记线段BC与AD组成的图形为G.
① 直接写出点C,D的坐标;
② 若双曲线与图形G恰有一个公共点,结合函数图象,求k的取值范围.
25.如图,在Rt△OAB中,∠OAB=90°,∠ABO=30°,C为OB边的中点,⊙O经过点C,BD与⊙O相切于点D.
(1)求证:AB与⊙O相切;
(2)若AB=2,求AD的长.
26.如图所示,有一直角梯形的苗圃,它的两邻边借用了成135的墙角(墙足够长),另外两边由总长为30 m的篱笆围成.
(1)苗圃的面积y(单位:m2)是BC的长x(单位:m)的函数,求该函数的表达式,并写出自变量x的取值范围;
(2)判断苗圃的面积能否达到160 m2 ,并说明理由.
27.在平面直角坐标系xOy中,点A(1+a,y1),B(b,y2)是抛物线上不重合的两点.
(1)当a=1,时,求b的值;
(2)若对于,都有,求a的取值范围.
28.已知△ABE,将△ABE绕点A逆时针旋转a (0°(1)①依题意补全图1;
②若FC垂直BE,直接写出a的值;
(2)如图2,过B作AC的平行线BD,与FE的延长线交于点D,FE交AC于点G,取FD的中点M和BC的中点N,写出线段MN与FG的数量关系,并证明.
每日接待游客人数 (单位:万人) 游玩环境评价
0≤x<5 好
5≤x<10 一般
10≤x<15 拥挤
15≤x<20 严重拥挤
图1
图2
图2
图1
初三数学第 1 页 共 2 页
初三数学第 1 页 共 2 页
一、单项选择题(下列各小题均有四个选项,其中只有一个选项符合题意. 共16分,每小题2分)
1.下列图形中,是轴对称图形但不是中心对称图形的是( ).
A. B. C. D.
2.在2025年春节档期,电影市场的热度持续高涨.电影《哪吒之魔童闹海》上映前三日,总票房便达到15.81亿元,这部电影在上映前三日平均每天的票房为( ).
A.元 B. 元 C. 元 D.元
3.实数在数轴上的对应点的位置如图所示,则正确的结论是( ).
A. B. C. D.
4.正六边形的每个内角度数为( ).
A.60° B.120° C. 135° D.150°
5.用配方法解一元二次方程,下列变形正确的是( ).
A. B. C. D.
6.如图,AB是⊙O的直径,C,D是⊙O上的两点.若∠CAB=65°,
则∠ADC的度数为( ).
A.65° B. 35° C.32.5° D.25°
7.把不等式组中两个不等式的解集在数轴上表示出来,正确的是( ).
A. B. C. D.
8.某景区为了解游客人数的变化规律,提高旅游服务质量,收集并整理了某月(30天)接待游客人数(单位:万人)的数据,绘制了下面的统计图和统计表.
根据以上信息,以下四个判断中,正确的是( ).
① 该景区这个月游玩环境评价为“拥挤或严重拥挤”的天数仅有4天;
② 该景区这个月每日接待游客人数的中位数在5~10万人之间;
③ 该景区这个月平均每日接待游客人数低于5万人;
④ 这个月1日至5日的五天中,如果某人曾经随机选择其中的两天到该景区游玩,那么他 “这两天游玩环境评价均为好”的可能性为.
A.①② B.②③ C.①④ D.②④
二、填空题(本题共16分,每小题2分)
9.若在实数范围内有意义,则实数的取值范围是 .
10.分解因式: .
11.如果,那么代数式的值为 .
12.半径为6cm,圆心角为40°的扇形的面积为 cm2.
13.如图,在矩形ABCD中,E是边CD的延长线上一点,连接BE交边AD于点F.若AB=4,BC=6,DE=2,则AF的长为 .
14.在一个布口袋里装有白、红、黑三种颜色的小球,它们除颜色外没有任何区别,其中白球2只,红球4只,黑球3只,将袋中的球搅匀,随机从袋中取出1只球,则取出黑球的概率是 .
15.《九章算术》中记载:“今有大器五、小器一容三斛;大器一、小器五容二斛.问大小器各容几何?”其大意是:今有大容器5个,小容器1个,总容量为3斛;大容器1个,小容器5个,总容量为2斛.问大容器、小容器的容量各是多少?设大容器容量为x斛,小容器容量为y斛,根据题意,可列方程组为 .(斛:古量器名,容量单位)
16. 某快递公司的快递件分为甲类件和乙类件,快递员送甲类件每件收入1元,送乙类件每件收入2元. 累计工作1小时,只送甲类件,最多可送30件,只送乙类件,最多可送10件;累计工作2小时,只送甲类件,最多可送55件,只送乙类件,最多可送20件;……,经整理形成统计表如下:
累计工作时长最多件数 (时)种类 (件) 1 2 3 4 5 6 7 8
甲类件 30 55 80 100 115 125 135 145
乙类件 10 20 30 40 50 60 70 80
(1)如果快递员一天工作8小时,且只送某一类件,那么他一天的最大收入为 元;
(2)如果快递员一天累计送x小时甲类件,y小时乙类件,且x+y=8,x,y均为正整数,那么他一天的最大收入为 元.
三、解答题(本题共68分,第17、18、19每题各5分;第20、21、22、24、25、26、27题,每题各6分;第23题4分;第28题7分)
17. 计算: .
18. 解不等式组:
19. 如图,在△ABC中,∠CAB=∠CBA,AD⊥BC于点D,BE⊥AC于点E.
求证:AD=BE.
20.关于x的一元二次方程有两个不相等的实数根.
(1)求n的取值范围;
(2)若n为取值范围内的最小整数,求此方程的根.
21.如图,在△ABC中,,D为AB边上一点,连接CD,E为CD中点,连接BE并延长至点F,使得EF=EB,连接DF交AC于点G,连接CF.
(1)求证:四边形DBCF是平行四边形;
(2)若,,,求CD的长.
22. 下面是某同学设计的“作圆的内接正方形”的尺规作图的过程.
已知:如图1,⊙O.
求作:正方形ABCD,使正方形ABCD内接于⊙O.
作法:如图2,
① 过点O作直线AC,交⊙O于点A和C;
② 作线段AC的垂直平分线MN,交⊙O于点B和D;
③ 顺次连接AB,BC,CD和DA;
则正方形ABCD就是所求作的图形.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明: ∵ AC是⊙O的直径,
∴ ∠ABC =∠ADC = °,
又∵点B在线段AC的垂直平分线上,
∴ AB = BC,
∴ ∠BAC = ∠BCA = °.
同理 ∠DAC = 45°.
∴ ∠BAD = ∠BAC +∠DAC = 45° + 45° = 90°.
∴ ∠DAB = ∠ABC = ∠ADC = 90°,
∴ 四边形ABCD是矩形( )(填依据),
又∵ AB = BC,
∴ 四边形ABCD是正方形.
23. 进位制是人们为了记数和运算方便而约定的记数系统.约定逢三进一就是三进制,用数字0,1,2记数,三进制数可以转换为十进制数.例如,三进制数1212记为,由,可得是十进制数50.
(1)将转换为十进制数,结果是_______;
(2)对于一个用三进制表示的正整数,有下列两个结论:
①如果这个数的末位数字能被2整除,那么这个数就能被2整除;
②如果这个数的所有数位上的数字之和能被2整除,那么这个数就能被2整除.
从中选出正确结论,并以四位的三进制数为例,说明该结论正确的道理.
24.在平面直角坐标系xOy中,直线经过点A(1,m),B(,).
(1)求b和m的值;
(2)将点B向右平移到y轴上,得到点C,设点B关于原点的对称点为D,记线段BC与AD组成的图形为G.
① 直接写出点C,D的坐标;
② 若双曲线与图形G恰有一个公共点,结合函数图象,求k的取值范围.
25.如图,在Rt△OAB中,∠OAB=90°,∠ABO=30°,C为OB边的中点,⊙O经过点C,BD与⊙O相切于点D.
(1)求证:AB与⊙O相切;
(2)若AB=2,求AD的长.
26.如图所示,有一直角梯形的苗圃,它的两邻边借用了成135的墙角(墙足够长),另外两边由总长为30 m的篱笆围成.
(1)苗圃的面积y(单位:m2)是BC的长x(单位:m)的函数,求该函数的表达式,并写出自变量x的取值范围;
(2)判断苗圃的面积能否达到160 m2 ,并说明理由.
27.在平面直角坐标系xOy中,点A(1+a,y1),B(b,y2)是抛物线上不重合的两点.
(1)当a=1,时,求b的值;
(2)若对于,都有,求a的取值范围.
28.已知△ABE,将△ABE绕点A逆时针旋转a (0°
②若FC垂直BE,直接写出a的值;
(2)如图2,过B作AC的平行线BD,与FE的延长线交于点D,FE交AC于点G,取FD的中点M和BC的中点N,写出线段MN与FG的数量关系,并证明.
每日接待游客人数 (单位:万人) 游玩环境评价
0≤x<5 好
5≤x<10 一般
10≤x<15 拥挤
15≤x<20 严重拥挤
图1
图2
图2
图1
初三数学第 1 页 共 2 页
初三数学第 1 页 共 2 页
同课章节目录
