数学:1.6《三角函数模型的简单应用》课件(2)(新人教a版必修4)
文档属性
| 名称 | 数学:1.6《三角函数模型的简单应用》课件(2)(新人教a版必修4) |  | |
| 格式 | rar | ||
| 文件大小 | 61.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-03 18:36:00 | ||
图片预览




文档简介
课件18张PPT。1.6 三角函数模型的简单应用 第二课时 问题提出 2.三角函数的应用十分广泛, 对于与角有关的实际问题,我们可以建立一个三角函数,通过研究其图象和性质或进行定量分析,就能解决相应问题.这是一种数学思想,需要结合具体问题的研究才能领会和掌握.三角函数性质
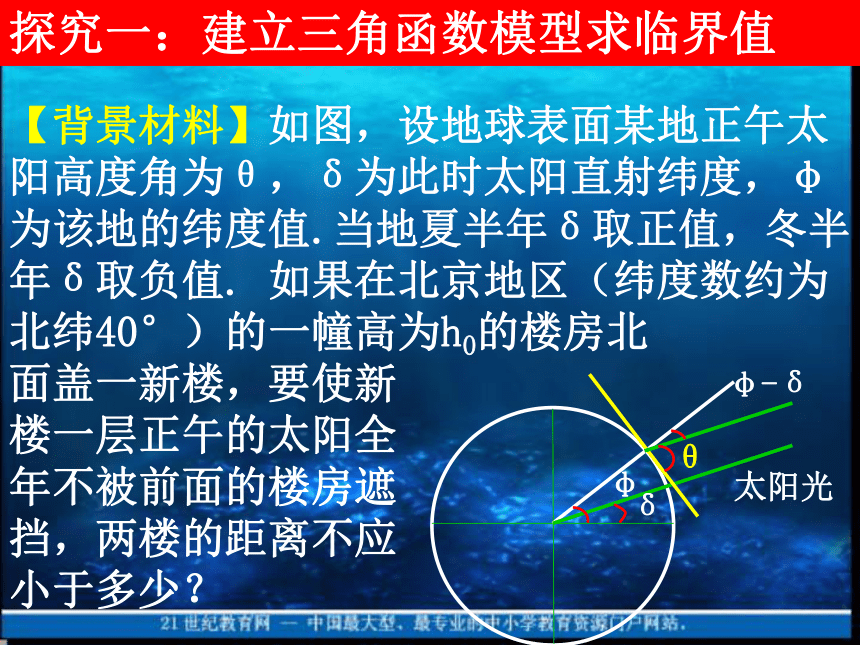
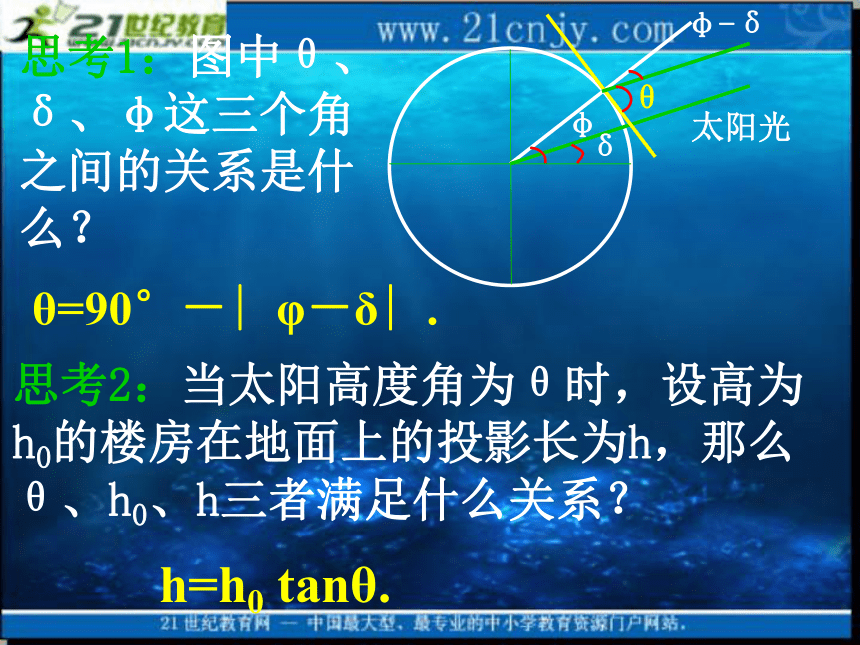
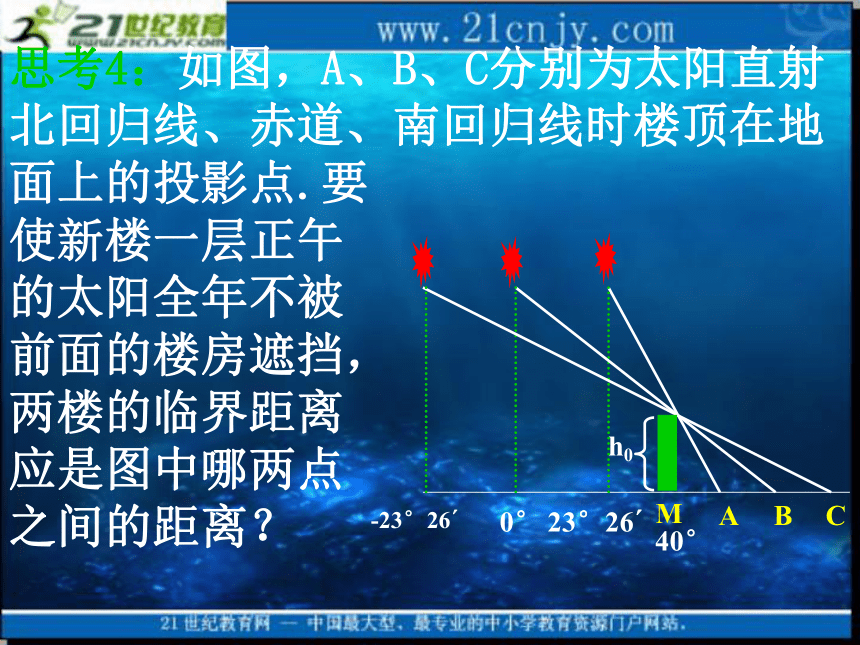
的简单应用探究一:建立三角函数模型求临界值 思考1:图中θ、δ、φ这三个角之间的关系是什么? θ=90°-∣φ-δ∣.思考2:当太阳高度角为θ时,设高为h0的楼房在地面上的投影长为h,那么θ、h0、h三者满足什么关系? h=h0 tanθ. 思考3:根据地理知识,北京地区一年中,正午太阳直射什么纬度位置时,物体的影子最短或影子最长?太阳直射北回归线时物体的影子最短,直射南回归线时物体的影子最长.思考4:如图,A、B、C分别为太阳直射北回归线、赤道、南回归线时楼顶在地面上的投影点.要
使新楼一层正午
的太阳全年不被
前面的楼房遮挡,
两楼的临界距离
应是图中哪两点
之间的距离?思考5:右图中∠C的度数是多少?MC的长度如何计算?思考6:综上分析,要使新楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离不应小于多少?探究二:建立三角函数模型解决最值问题 思考1:修建水渠的成本可以用哪个几何量来反映?思考2:设想将AD+DC+CB表示成某个变量的函数,那么自变量如何选取?思考3:取∠BCE=x为自变量,设y=AD+DC+CB,那么如何建立y与x的函数关系?思考5:注意到S、h为常数,要使y的值最小,只需研究哪个三角函数的最小值?思考6:对于函数
你有什么办法求出当x为何值时,k取最小值? P(-sinx,cosx)A(0,2)思考7:如何对原问题作出相应回答? 修建时使梯形的腰与底边的夹角为60°,才能使修建成本最低. 理论迁移 例1 某市的纬度是北纬21°34′,小王想在某住宅小区买房,该小区的楼高7层,每层3米,楼与楼之间相距15米,要使所买楼房在一年四季正午的太阳不被前面的楼房遮挡,最低应该选择第几层的房?三楼 例2 如图,甲船在点A处测得乙船在北偏东60°的B处,并以每小时10海里的速度向正北方向行使,若甲船沿北偏东θ角方向直线航行,并与乙船在C处相遇,求甲船的航速.小结作业 2.在解决实际问题时,要学会具体问题
具体分析,充分运用数形结合的思想,
灵活的运用三角函数的图象和性质进行
解答. 作业:
P65习题1.6A组:1,2,3.
的简单应用探究一:建立三角函数模型求临界值 思考1:图中θ、δ、φ这三个角之间的关系是什么? θ=90°-∣φ-δ∣.思考2:当太阳高度角为θ时,设高为h0的楼房在地面上的投影长为h,那么θ、h0、h三者满足什么关系? h=h0 tanθ. 思考3:根据地理知识,北京地区一年中,正午太阳直射什么纬度位置时,物体的影子最短或影子最长?太阳直射北回归线时物体的影子最短,直射南回归线时物体的影子最长.思考4:如图,A、B、C分别为太阳直射北回归线、赤道、南回归线时楼顶在地面上的投影点.要
使新楼一层正午
的太阳全年不被
前面的楼房遮挡,
两楼的临界距离
应是图中哪两点
之间的距离?思考5:右图中∠C的度数是多少?MC的长度如何计算?思考6:综上分析,要使新楼一层正午的太阳全年不被前面的楼房遮挡,两楼的距离不应小于多少?探究二:建立三角函数模型解决最值问题 思考1:修建水渠的成本可以用哪个几何量来反映?思考2:设想将AD+DC+CB表示成某个变量的函数,那么自变量如何选取?思考3:取∠BCE=x为自变量,设y=AD+DC+CB,那么如何建立y与x的函数关系?思考5:注意到S、h为常数,要使y的值最小,只需研究哪个三角函数的最小值?思考6:对于函数
你有什么办法求出当x为何值时,k取最小值? P(-sinx,cosx)A(0,2)思考7:如何对原问题作出相应回答? 修建时使梯形的腰与底边的夹角为60°,才能使修建成本最低. 理论迁移 例1 某市的纬度是北纬21°34′,小王想在某住宅小区买房,该小区的楼高7层,每层3米,楼与楼之间相距15米,要使所买楼房在一年四季正午的太阳不被前面的楼房遮挡,最低应该选择第几层的房?三楼 例2 如图,甲船在点A处测得乙船在北偏东60°的B处,并以每小时10海里的速度向正北方向行使,若甲船沿北偏东θ角方向直线航行,并与乙船在C处相遇,求甲船的航速.小结作业 2.在解决实际问题时,要学会具体问题
具体分析,充分运用数形结合的思想,
灵活的运用三角函数的图象和性质进行
解答. 作业:
P65习题1.6A组:1,2,3.
