1.2.1 平方差公式 课件(共23张PPT)
文档属性
| 名称 | 1.2.1 平方差公式 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 368.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-24 13:07:13 | ||
图片预览








文档简介
(共23张PPT)
平方差公式
七年级下册 第一章 1.2.1
学习目标
1.理解平方差公式的几何意义,能用数学语言表述( + )( )= 2 2。
2.能熟练运用平方差公式进行整式乘法运算;
3.会利用平方差公式解决简单的实际问题。
复习回顾
多项式乘多项式的法则是什么?
法则:
多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn (a,b,m,n都是单项式)
新知探究
多项式x+y与xy相乘,其积为多少?
说一说
解:(x+y)(xy)=x2xy+xyy2
=x2y2.
平方差公式: (x+y)(xy)=x2y2
新知探究
几何背景
已知大正方形的边长为a,小正方形的边长为b,求阴影部分的面积。
解:大正方形的面积为a2,
小正方形的面积为b2,
故阴影部分的面积为a2b2。
新知探究
几何背景
将剩余部分沿虚线剪开后,拼成一个如下图所示的长方形,求该长方形的面积。
解:该长方形的长为a+b,
该长方形的宽为ab ,
故长方形的面积为(a+b)(ab)=a2b2 。
新知探究
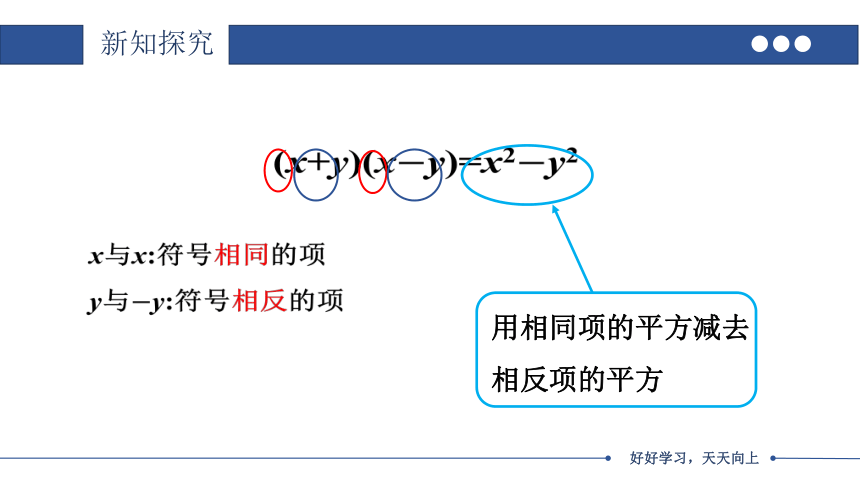
(x+y)(xy)=x2y2
x与x:符号相同的项
y与y:符号相反的项
用相同项的平方减去相反项的平方
例题探究
例1 计算:(1) (2x+1)(2x-1); (2) (x+2y)(x-2y).
解:(1) 原式= 4x2-2x+2x-1
= 4x2-1.
(2) 原式=x2-2xy+2xy-4y2
= x2-4y2.
多项式乘多项式:
例题探究
例1 计算:(1) (2x+1)(2x-1); (2) (x+2y)(x-2y).
解:(1) 原式= (2x)2-12
= 4x2-1.
(2) 原式=x2-(2y)2
= x2-4y2.
平方差公式:
与不用平方差公式计算相比,哪种方法更简便?
例2 运用平方差公式计算: .
例题探究
解:将平方差公式中的x用-2x代替,y用y代替,可得
=
=.
例3 运用平方差公式计算:(4a+b)(-b+4a).
例题探究
解:由平方差公式得
(4a+b)(-b+4a)=(4a+b)(4a-b)
=(4a)2-b2
=16a2-b2.
将括号内的式子转化为平方差公式的形式.
例题探究
一般步骤:
1.利用加法交换律调整括号内项的位置,使之与公式左边相对应(已对应的无需调整)
2.找准哪个单项式或多项式分别代表公式中的“x”和“y”
3.套用公式计算,注意将底数带上括号
例4 计算:1002×998.
例题探究
运用平方差公式可以简化一些运算.
解:1002×998 = (1000+2)(1000-2)
= 10002-22
= 1000000-4
= 999996
1.计算:(1) (3x+y)(3xy);(2) (m-n)(m+n);
(3) (1+5x)(15x);(4) (4a-b)(4a-b).
课堂练习
解:(1) 原式 = (3x)2-y2
= 9x2-y2.
(2) 原式 = (m)2-n2
= m 2-n2.
1.计算:(1) (3x+y)(3xy);(2) (m-n)(m+n);
(3) (1+5x)(15x);(4) (4a-b)(4a-b).
课堂练习
解:(3) 原式 = (1)2-(5x)2
=1-25x2.
(4) 原式 = (4a)(-b+4a)
=()2-(4a)2
=b2-16a2.
2.计算:(1) 202×198;(2) 49.8×50.2 .
课堂练习
解:(1) 原式= (200+2)(200-2)
=200222
=400004
=39996
(2) 原式= (500.2)(50+0.2)
=5020.22
=25000.04
=2499.96
3.下列各式能用平方差公式计算的是 ( )
A.(3a+b)(a-b)
B.(3a+b)(-3a-b)
C.(-3a-b)(-3a+b)
D.(-3a+b)(3a-b)
课堂练习
C
4.下列运用平方差公式计算错误的是 ( )
A.(a+5b)(a-5b)=a2-25b2
B.(x+1)(x-1)=x2-1
C.(2x+1)(2x-1)=2x2-1
D.(-a+2b)(-a-2b)=a2-4b2
课堂练习
C
5.从前,古希腊一位庄园主把一块边长为a米(a>6)的正方形土地租给某租户.第二年,他对该租户说:“我把这块地的一边增加6米,与其相邻的另一边减少6米,变成长方形土地继续租给你,租金不变,你也没有吃亏,你看如何 ”如果这样,你觉得该租户的租地面积 ( )
A.没有变化 B.变大了 C.变小了 D.无法确定
课堂练习
C
6.若(x+y+1)(x+y-1)=8,则x+y的值为 ( )
A.3
B.±3
C.-3
D.±5
课堂练习
B
课堂小结
一般步骤:
1.利用加法交换律调整括号内项的位置,使之与公式左边相对应(已对应的无需调整)
2.找准哪个单项式或多项式分别代表公式中的“x”和“y”
3.套用公式计算,注意将底数带上括号
平方差公式: (x+y)(xy)=x2y2
课后作业
课堂作业:P22 T1
平方差公式
七年级下册 第一章 1.2.1
学习目标
1.理解平方差公式的几何意义,能用数学语言表述( + )( )= 2 2。
2.能熟练运用平方差公式进行整式乘法运算;
3.会利用平方差公式解决简单的实际问题。
复习回顾
多项式乘多项式的法则是什么?
法则:
多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加.
(a+b)(m+n)=am+an+bm+bn (a,b,m,n都是单项式)
新知探究
多项式x+y与xy相乘,其积为多少?
说一说
解:(x+y)(xy)=x2xy+xyy2
=x2y2.
平方差公式: (x+y)(xy)=x2y2
新知探究
几何背景
已知大正方形的边长为a,小正方形的边长为b,求阴影部分的面积。
解:大正方形的面积为a2,
小正方形的面积为b2,
故阴影部分的面积为a2b2。
新知探究
几何背景
将剩余部分沿虚线剪开后,拼成一个如下图所示的长方形,求该长方形的面积。
解:该长方形的长为a+b,
该长方形的宽为ab ,
故长方形的面积为(a+b)(ab)=a2b2 。
新知探究
(x+y)(xy)=x2y2
x与x:符号相同的项
y与y:符号相反的项
用相同项的平方减去相反项的平方
例题探究
例1 计算:(1) (2x+1)(2x-1); (2) (x+2y)(x-2y).
解:(1) 原式= 4x2-2x+2x-1
= 4x2-1.
(2) 原式=x2-2xy+2xy-4y2
= x2-4y2.
多项式乘多项式:
例题探究
例1 计算:(1) (2x+1)(2x-1); (2) (x+2y)(x-2y).
解:(1) 原式= (2x)2-12
= 4x2-1.
(2) 原式=x2-(2y)2
= x2-4y2.
平方差公式:
与不用平方差公式计算相比,哪种方法更简便?
例2 运用平方差公式计算: .
例题探究
解:将平方差公式中的x用-2x代替,y用y代替,可得
=
=.
例3 运用平方差公式计算:(4a+b)(-b+4a).
例题探究
解:由平方差公式得
(4a+b)(-b+4a)=(4a+b)(4a-b)
=(4a)2-b2
=16a2-b2.
将括号内的式子转化为平方差公式的形式.
例题探究
一般步骤:
1.利用加法交换律调整括号内项的位置,使之与公式左边相对应(已对应的无需调整)
2.找准哪个单项式或多项式分别代表公式中的“x”和“y”
3.套用公式计算,注意将底数带上括号
例4 计算:1002×998.
例题探究
运用平方差公式可以简化一些运算.
解:1002×998 = (1000+2)(1000-2)
= 10002-22
= 1000000-4
= 999996
1.计算:(1) (3x+y)(3xy);(2) (m-n)(m+n);
(3) (1+5x)(15x);(4) (4a-b)(4a-b).
课堂练习
解:(1) 原式 = (3x)2-y2
= 9x2-y2.
(2) 原式 = (m)2-n2
= m 2-n2.
1.计算:(1) (3x+y)(3xy);(2) (m-n)(m+n);
(3) (1+5x)(15x);(4) (4a-b)(4a-b).
课堂练习
解:(3) 原式 = (1)2-(5x)2
=1-25x2.
(4) 原式 = (4a)(-b+4a)
=()2-(4a)2
=b2-16a2.
2.计算:(1) 202×198;(2) 49.8×50.2 .
课堂练习
解:(1) 原式= (200+2)(200-2)
=200222
=400004
=39996
(2) 原式= (500.2)(50+0.2)
=5020.22
=25000.04
=2499.96
3.下列各式能用平方差公式计算的是 ( )
A.(3a+b)(a-b)
B.(3a+b)(-3a-b)
C.(-3a-b)(-3a+b)
D.(-3a+b)(3a-b)
课堂练习
C
4.下列运用平方差公式计算错误的是 ( )
A.(a+5b)(a-5b)=a2-25b2
B.(x+1)(x-1)=x2-1
C.(2x+1)(2x-1)=2x2-1
D.(-a+2b)(-a-2b)=a2-4b2
课堂练习
C
5.从前,古希腊一位庄园主把一块边长为a米(a>6)的正方形土地租给某租户.第二年,他对该租户说:“我把这块地的一边增加6米,与其相邻的另一边减少6米,变成长方形土地继续租给你,租金不变,你也没有吃亏,你看如何 ”如果这样,你觉得该租户的租地面积 ( )
A.没有变化 B.变大了 C.变小了 D.无法确定
课堂练习
C
6.若(x+y+1)(x+y-1)=8,则x+y的值为 ( )
A.3
B.±3
C.-3
D.±5
课堂练习
B
课堂小结
一般步骤:
1.利用加法交换律调整括号内项的位置,使之与公式左边相对应(已对应的无需调整)
2.找准哪个单项式或多项式分别代表公式中的“x”和“y”
3.套用公式计算,注意将底数带上括号
平方差公式: (x+y)(xy)=x2y2
课后作业
课堂作业:P22 T1
同课章节目录
