算法的概念
图片预览





文档简介
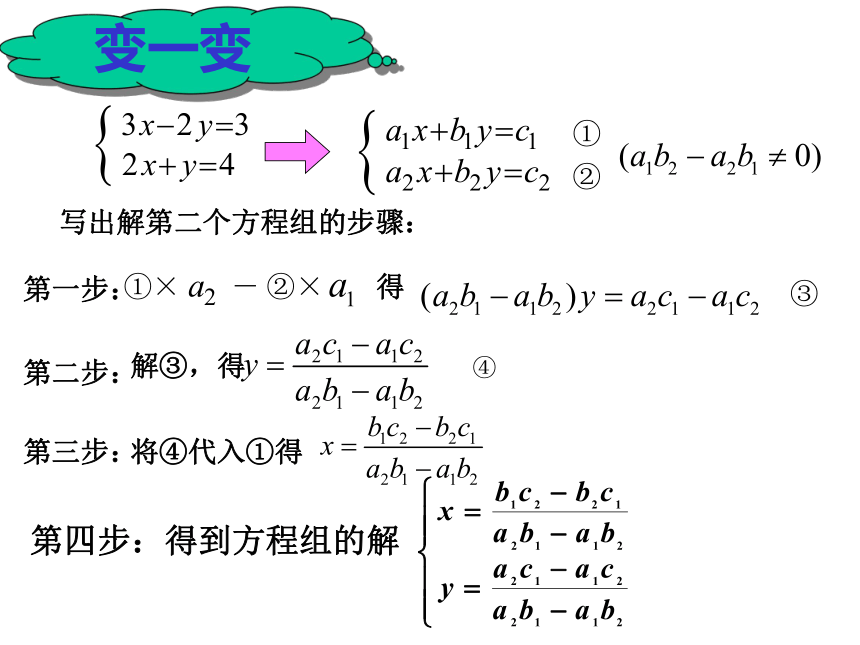
课件17张PPT。算法的概念算筹算盘计算器计算机第一步:第二步:第三步:(消元)①+②×2,得 ③解③得将 代入①,得 写一写 得到方程组的解第四步:写出解第二个方程组的步骤:第一步:第二步:第三步:③解③,得 ④将④代入①得变一变第四步:得到方程组的解 这 两个解方程组算法的适用范围有何不同?第一步:第二步:第三步:③解③,得 ④将④带入①得①②解③得③---------------------------------------------------第四步:得到方程组解第四步:得到方程组的解定义:在数学中,算法通常是指按照一定规则
解决某一类问题的明确和有限的步骤。算法(algorithm)一词出现于12世纪,指的是用阿拉伯数字进行算术运算的过程。现在,算法通常可以编成计算机程序,让计算机执行并解决问题。的解有人对歌德巴赫猜想“任何大于4的偶数都能写成两个质数之和”设计了如下操作步骤:第一步:检验6=3+3第二步:检验8=3+5。。。利用计算机无穷地进行下去!请问,利用这种程序能够证明猜想的正确性吗?第三步:检验10=5+5这是一种算法吗?
第四步,用5除35,得到余数0.因为余数为0,
所以5能整除35.因此,35不是质数.
例1、 (1)设计一个算法,判断7是否为质数.(2)的算法如下:
第一步,用2除35,得到余数1.因为余数不为0,
所以2不能整除35.第二步,用3除35,得到余数2.因为余数不为0,
所以3不能整除35.第三步,用4除35,得到余数3.因为余数不为0,
所以4不能整除35.(2)设计一个算法,判断35是否为质数例1、(3)设计一个算法,判断37是否为质数。。。第1步,用2除37,得到余数1.因为余数不为0,
所以2不能整除37.
第2步,用3除37,得到余数2.因为余数不为0,
所以3不能整除37.第3步,用4除37,得到余数3.因为余数不为0,
所以4不能整除37.第35步,用36除37,得到余数1.因为余数不为0,所以36不能整除37.因此,37不是质数.变式:设计一个算法,判断n(n>2)是否为质数.解:算法如下:
第1步,给定大于2的整数n.第2步,令i=2.第3步,用i除n,得到余数r.第4步,判断“r=0”是否成立。若是,则n不是质数,结束算法;否则,将i的值增加1,仍用i表示。第5步,判断“i>(n-1)”是否成立。若是,则n是质数,结束算法;否则,返回第三步。三、练习1、写出求1+2+3+4+5+6的一个算法解:算法 1:第一步:计算1+2 得到 3;第二步:将第一步中的运算结果 3 与 3 相加得到 6;第三步:第直步中的运算结果 6 与 4 相加得到 10;第四步:将第三步中的运算结果 10 与 5 相加得到 15;第五步:将第四步中的运算结果 15 与 6 相加得到 21。算法2:第一步:取n=6;第三步:输出结果。算法3:第一步:将原式变形为(1+6)+(2+5)+(3+4)=3×7;第二步:计算 3×7;第三步:输出运算结果。第二步:计算 ;2、任意给定的一个正实数,设计一个算法求以这个数为半径的圆的面积。算法步骤:第一步:输入任意一个正实数 r;第二步:计算以r为半径的圆的面积:第三步:输出圆的面积 S。算法步骤:第一步:依次以2 ~(n – 1)为除数除 n ,检查余数是否为0;若是,则是 n 的因数;若不是,则不是 n 的因数;第二步:在 n 的因数中加入 1 和 n;第三步:输出n的所有因数。3、任意给定一个大于 1 的正整数 n ,设计一个算法求出 n 的所有因数。第一步:输入一个大于1的n;
第二步:令i=1;
第三步:用i除n,得到余数为r,判断r是否为0, 若是,则输出i,并执行第四步;否则不输出,直接执行第四步;
第四步:令i = i +1
第五步:判断i是否大于n,若是则结束算法;否则执行第三步;
3、任意给定一个大于 1 的正整数 n ,设计一个算法求出 n 的所有因数。知识结构算法的自然语言表达 算法的特征 算法的概念算法课堂小结作业2、求1×3 × 5 × 7 × 9 × 11的值,写出其算法。1、写出解不等式 的一个算法。写出求1+2+3+ +100的和的算法3、4、(选做)网上查阅“从算筹到电脑——计算工具的演变”。
解决某一类问题的明确和有限的步骤。算法(algorithm)一词出现于12世纪,指的是用阿拉伯数字进行算术运算的过程。现在,算法通常可以编成计算机程序,让计算机执行并解决问题。的解有人对歌德巴赫猜想“任何大于4的偶数都能写成两个质数之和”设计了如下操作步骤:第一步:检验6=3+3第二步:检验8=3+5。。。利用计算机无穷地进行下去!请问,利用这种程序能够证明猜想的正确性吗?第三步:检验10=5+5这是一种算法吗?
第四步,用5除35,得到余数0.因为余数为0,
所以5能整除35.因此,35不是质数.
例1、 (1)设计一个算法,判断7是否为质数.(2)的算法如下:
第一步,用2除35,得到余数1.因为余数不为0,
所以2不能整除35.第二步,用3除35,得到余数2.因为余数不为0,
所以3不能整除35.第三步,用4除35,得到余数3.因为余数不为0,
所以4不能整除35.(2)设计一个算法,判断35是否为质数例1、(3)设计一个算法,判断37是否为质数。。。第1步,用2除37,得到余数1.因为余数不为0,
所以2不能整除37.
第2步,用3除37,得到余数2.因为余数不为0,
所以3不能整除37.第3步,用4除37,得到余数3.因为余数不为0,
所以4不能整除37.第35步,用36除37,得到余数1.因为余数不为0,所以36不能整除37.因此,37不是质数.变式:设计一个算法,判断n(n>2)是否为质数.解:算法如下:
第1步,给定大于2的整数n.第2步,令i=2.第3步,用i除n,得到余数r.第4步,判断“r=0”是否成立。若是,则n不是质数,结束算法;否则,将i的值增加1,仍用i表示。第5步,判断“i>(n-1)”是否成立。若是,则n是质数,结束算法;否则,返回第三步。三、练习1、写出求1+2+3+4+5+6的一个算法解:算法 1:第一步:计算1+2 得到 3;第二步:将第一步中的运算结果 3 与 3 相加得到 6;第三步:第直步中的运算结果 6 与 4 相加得到 10;第四步:将第三步中的运算结果 10 与 5 相加得到 15;第五步:将第四步中的运算结果 15 与 6 相加得到 21。算法2:第一步:取n=6;第三步:输出结果。算法3:第一步:将原式变形为(1+6)+(2+5)+(3+4)=3×7;第二步:计算 3×7;第三步:输出运算结果。第二步:计算 ;2、任意给定的一个正实数,设计一个算法求以这个数为半径的圆的面积。算法步骤:第一步:输入任意一个正实数 r;第二步:计算以r为半径的圆的面积:第三步:输出圆的面积 S。算法步骤:第一步:依次以2 ~(n – 1)为除数除 n ,检查余数是否为0;若是,则是 n 的因数;若不是,则不是 n 的因数;第二步:在 n 的因数中加入 1 和 n;第三步:输出n的所有因数。3、任意给定一个大于 1 的正整数 n ,设计一个算法求出 n 的所有因数。第一步:输入一个大于1的n;
第二步:令i=1;
第三步:用i除n,得到余数为r,判断r是否为0, 若是,则输出i,并执行第四步;否则不输出,直接执行第四步;
第四步:令i = i +1
第五步:判断i是否大于n,若是则结束算法;否则执行第三步;
3、任意给定一个大于 1 的正整数 n ,设计一个算法求出 n 的所有因数。知识结构算法的自然语言表达 算法的特征 算法的概念算法课堂小结作业2、求1×3 × 5 × 7 × 9 × 11的值,写出其算法。1、写出解不等式 的一个算法。写出求1+2+3+ +100的和的算法3、4、(选做)网上查阅“从算筹到电脑——计算工具的演变”。
