第十八章平行四边形18.2..2《菱形》第一课时:菱形的性质 教学设计
文档属性
| 名称 | 第十八章平行四边形18.2..2《菱形》第一课时:菱形的性质 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 248.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-24 00:00:00 | ||
图片预览

文档简介
第十八章平行四边形
18.2..2《菱形》
第一课时:菱形的性质 教学设计
一、教学目标
知识目标
1.助力学生理解菱形的定义,牢固掌握其特殊性质。
2.引导学生理解菱形面积公式,使其能依据实际情况,恰当选择方法计算菱形面积。
3.借助观察、实验、猜想、验证、推理交流等数学活动,全方位提升学生的合情推理、动手操作能力,以及应用数学的意识与能力。
4.运用菱形知识解决具体问题,着重培养学生的逻辑推理与演绎能力。
核心素养目标
1.在应用菱形性质的过程中,培养学生独立思考的良好习惯。
2.让学生在数学学习活动中收获成功体验,通过对菱形性质的探索学习,感悟其内在美与应用美。
二、教学重点、难点
重点
让学生精准掌握菱形的定义与性质。
引导学生学会菱形面积的求法。
难点
培养学生灵活运用菱形性质解决各类问题的能力。
三、教学过程
(一)“旧知搭桥,引入菱形”—— 复习启新
前面我们学行四边形和矩形,知道了矩形是由平行四边形角的变化得到,如果平行四边形有一个角是直角时,就成为了矩形.
如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢?
有一组邻边相等的平行四边形叫做菱形.
设计意图:通过复习旧知,搭建知识桥梁,让学生在已有知识基础上自然地引出菱形概念,体会知识的关联性与拓展性,降低新知识的接受难度,同时培养学生类比、迁移的数学思维。
(二)“巧手剪出菱形秘”—— 折一折、剪一剪
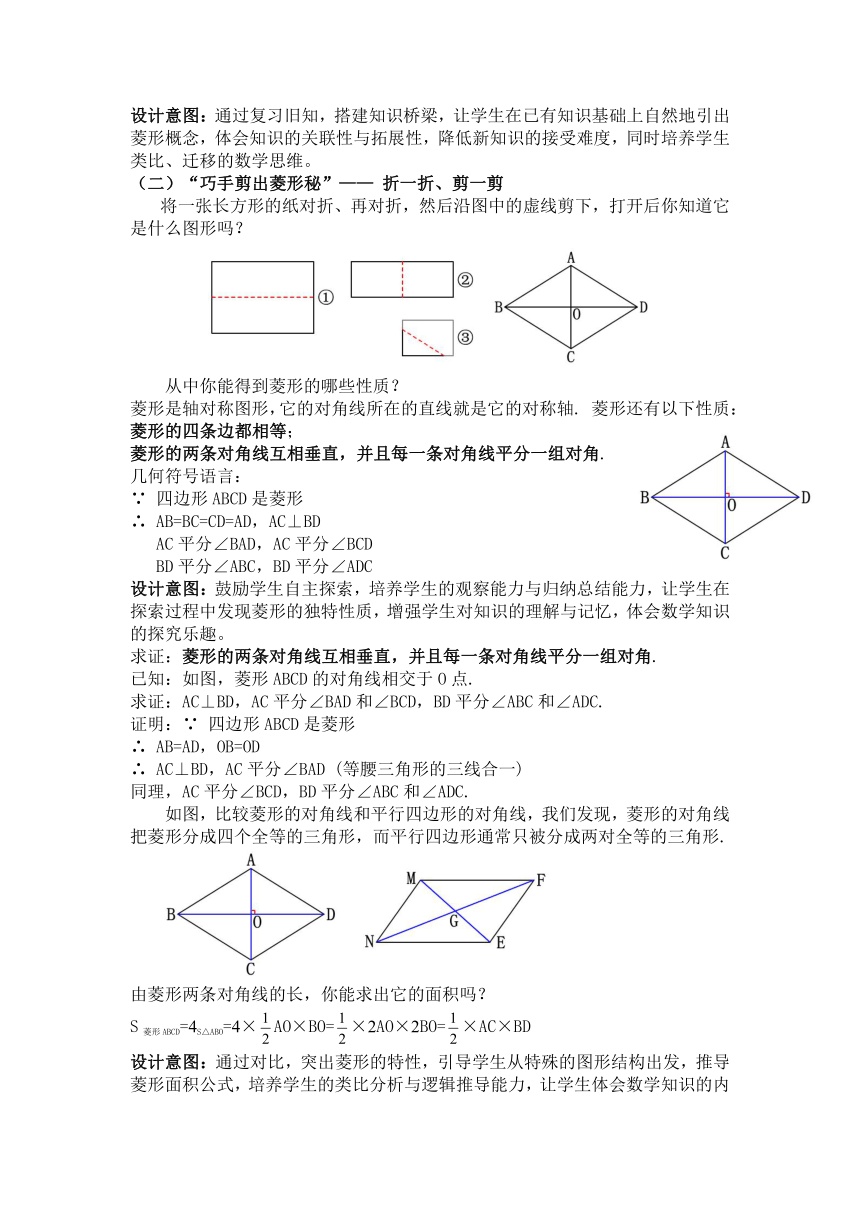
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开后你知道它是什么图形吗?
从中你能得到菱形的哪些性质?
菱形是轴对称图形,它的对角线所在的直线就是它的对称轴. 菱形还有以下性质:
菱形的四条边都相等;
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
几何符号语言:
∵ 四边形ABCD是菱形
∴ AB=BC=CD=AD,AC⊥BD
AC平分∠BAD,AC平分∠BCD
BD平分∠ABC,BD平分∠ADC
设计意图:鼓励学生自主探索,培养学生的观察能力与归纳总结能力,让学生在探索过程中发现菱形的独特性质,增强学生对知识的理解与记忆,体会数学知识的探究乐趣。
求证:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
已知:如图,菱形ABCD的对角线相交于O点.
求证:AC⊥BD,AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.
证明:∵ 四边形ABCD是菱形
∴ AB=AD,OB=OD
∴ AC⊥BD,AC平分∠BAD (等腰三角形的三线合一)
同理,AC平分∠BCD,BD平分∠ABC和∠ADC.
如图,比较菱形的对角线和平行四边形的对角线,我们发现,菱形的对角线把菱形分成四个全等的三角形,而平行四边形通常只被分成两对全等的三角形.
由菱形两条对角线的长,你能求出它的面积吗?
S菱形ABCD=4S△ABO=4×AO×BO=×2AO×2BO=×AC×BD
设计意图:通过对比,突出菱形的特性,引导学生从特殊的图形结构出发,推导菱形面积公式,培养学生的类比分析与逻辑推导能力,让学生体会数学知识的内在联系与转化思想。
(三)“生活中的菱形奥秘”—— 例题讲解
例3 如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
解:∵ 花坛ABCD的形状是菱形
∴ AC⊥BD,∠ABO=∠ABC=×60°=30°
在Rt△OAB中,AO=AB=×20=10
BO===
∴ 花坛的两条小路长AC=2AO=20(m)、BD=2BO=≈34.64(m)
花坛的面积S菱形ABCD=AC·BD=≈346.4(m2)
设计意图:引入实际生活案例,让学生运用所学菱形知识解决实际问题,感受数学知识在生活中的广泛应用,增强学生的数学应用意识与解决实际问题的能力,体会数学的实用价值。
(四)“智慧大闯关”—— 练习巩固
练习
1.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4.求AC和BD的长.
解:∵ 四边形ABCD是菱形
∴ AC⊥BD,BD=2OB,AC=2AO=8
在Rt△AOB中,OB===3
∴ BD=6
2.已知菱形的两对角线的长分别是6和8,求菱形的周长和面积.
解:∵ 四边形ABCD是菱形,且AC=8,BD=6
∴ AC⊥BD,AO=AC=4,BO=BD=3
在Rt△AOB中,AB===5
∴ C菱形ABCD=4×5=20
S菱形ABCD=×6×8=24
设计意图:通过多样化的练习题,巩固学生对菱形性质与面积公式的掌握程度,强化学生的解题技巧与运算能力,及时反馈学生的学习情况,便于教师进行针对性指导,同时以 “闯关” 形式增加练习的趣味性与挑战性,激发学生的学习积极性。
(五)“知识行囊大整理”—— 课堂小结
引导学生回顾本节课所学,分享收获。
鼓励学生提出尚未解决的问题。
设计意图:帮助学生梳理本节课的知识体系,强化重点内容,加深学生对知识的整体把握。同时,通过学生分享与提问,促进学生之间的交流与互动,培养学生的反思总结能力与问题意识,让学生学会自主学习。
四、教学总结
在本次《菱形的性质》教学旅程中,我们一同从平行四边形的旧知出发,踏上探索菱形这片新知识领域的征程。同学们积极参与动手操作,用自己的双手剪出了菱形的奥秘;在热烈的讨论与严谨的证明中,我们揭开了菱形神秘的面纱,发现了它独特的性质与美丽的面积公式。在解决生活中菱形花坛问题时,同学们更是展现出了将知识学以致用的能力。每一次思考、每一次回答问题,都是你们成长的足迹。希望同学们能将这份对数学的探索热情延续下去,在未来的数学学习中,继续发现更多的精彩与奥秘,用数学的眼光去观察世界,用数学的思维去解决问题,在数学的海洋里畅游得更远、更稳。
五、教学反思
成功之处:
教学方法上,充分利用动手操作活动,如折纸剪纸,极大地激发了学生的学习兴趣与主动性,让学生在实践中直观感受数学知识的形成过程,符合学生的认知规律,多数学生能积极参与并有所收获。
注重知识的关联性与逻辑性,通过复习平行四边形和矩形知识引入菱形,在探索菱形性质过程中不断对比与平行四边形的异同,帮助学生构建完整的知识体系,加深对知识的理解与记忆。
引入生活实例进行例题讲解,让学生切实体会到数学知识的实用性,增强了学生的数学应用意识,提高了学生解决实际问题的能力,课堂上学生对这类问题表现出较高的关注度与参与度。
不足之处:
在探索菱形性质环节,虽然大部分学生能积极参与,但仍有少数学生参与度不高,可能是操作活动的引导不够细致,未能充分考虑到不同层次学生的需求,导致部分学生在操作过程中遇到困难,影响了后续的思考与探索。
在证明菱形性质时,部分学生对证明思路的理解存在困难,反映出在逻辑推理教学方面,可能讲解速度过快,未能充分关注学生的思维节奏,需要进一步优化教学方法,给予学生更多思考与消化的时间。
改进措施:
在今后的教学中,针对操作活动,提前做好更充分的准备,如提供更详细的操作指南或进行示范,在活动过程中加强对学生的巡视与个别指导,确保每个学生都能顺利参与操作,从活动中有所收获。
在逻辑推理教学方面,放慢教学节奏,采用更多启发式提问,引导学生逐步理清证明思路,鼓励学生自主表达证明过程,及时纠正学生的错误,加强对学生逻辑思维能力的培养。同时,增加一些针对性的证明练习,让学生在实践中不断提高逻辑推理能力。
六、展示评价
评价维度 评价要点 评价等级(A. 优秀 B. 良好 C. 合格 D. 待提高)
学生参与度 是否积极参与课堂讨论、回答问题,主动参与探究活动
知识掌握 能否准确理解平行四边形对角线互相平分的性质,熟练运用性质进行证明和计算
思维能力 在观察、猜想、证明过程中,思维的敏捷性、逻辑性和创新性表现如何
合作交流 小组合作中,与小组成员沟通是否顺畅,能否积极贡献自己的想法,倾听他人意见
18.2..2《菱形》
第一课时:菱形的性质 教学设计
一、教学目标
知识目标
1.助力学生理解菱形的定义,牢固掌握其特殊性质。
2.引导学生理解菱形面积公式,使其能依据实际情况,恰当选择方法计算菱形面积。
3.借助观察、实验、猜想、验证、推理交流等数学活动,全方位提升学生的合情推理、动手操作能力,以及应用数学的意识与能力。
4.运用菱形知识解决具体问题,着重培养学生的逻辑推理与演绎能力。
核心素养目标
1.在应用菱形性质的过程中,培养学生独立思考的良好习惯。
2.让学生在数学学习活动中收获成功体验,通过对菱形性质的探索学习,感悟其内在美与应用美。
二、教学重点、难点
重点
让学生精准掌握菱形的定义与性质。
引导学生学会菱形面积的求法。
难点
培养学生灵活运用菱形性质解决各类问题的能力。
三、教学过程
(一)“旧知搭桥,引入菱形”—— 复习启新
前面我们学行四边形和矩形,知道了矩形是由平行四边形角的变化得到,如果平行四边形有一个角是直角时,就成为了矩形.
如果从边的角度,将平行四边形特殊化,内角大小保持不变仅改变边的长度让它有一组邻边相等,这个特殊的平行四边形叫什么呢?
有一组邻边相等的平行四边形叫做菱形.
设计意图:通过复习旧知,搭建知识桥梁,让学生在已有知识基础上自然地引出菱形概念,体会知识的关联性与拓展性,降低新知识的接受难度,同时培养学生类比、迁移的数学思维。
(二)“巧手剪出菱形秘”—— 折一折、剪一剪
将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开后你知道它是什么图形吗?
从中你能得到菱形的哪些性质?
菱形是轴对称图形,它的对角线所在的直线就是它的对称轴. 菱形还有以下性质:
菱形的四条边都相等;
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
几何符号语言:
∵ 四边形ABCD是菱形
∴ AB=BC=CD=AD,AC⊥BD
AC平分∠BAD,AC平分∠BCD
BD平分∠ABC,BD平分∠ADC
设计意图:鼓励学生自主探索,培养学生的观察能力与归纳总结能力,让学生在探索过程中发现菱形的独特性质,增强学生对知识的理解与记忆,体会数学知识的探究乐趣。
求证:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
已知:如图,菱形ABCD的对角线相交于O点.
求证:AC⊥BD,AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.
证明:∵ 四边形ABCD是菱形
∴ AB=AD,OB=OD
∴ AC⊥BD,AC平分∠BAD (等腰三角形的三线合一)
同理,AC平分∠BCD,BD平分∠ABC和∠ADC.
如图,比较菱形的对角线和平行四边形的对角线,我们发现,菱形的对角线把菱形分成四个全等的三角形,而平行四边形通常只被分成两对全等的三角形.
由菱形两条对角线的长,你能求出它的面积吗?
S菱形ABCD=4S△ABO=4×AO×BO=×2AO×2BO=×AC×BD
设计意图:通过对比,突出菱形的特性,引导学生从特殊的图形结构出发,推导菱形面积公式,培养学生的类比分析与逻辑推导能力,让学生体会数学知识的内在联系与转化思想。
(三)“生活中的菱形奥秘”—— 例题讲解
例3 如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长(结果保留小数点后两位)和花坛的面积(结果保留小数点后一位).
解:∵ 花坛ABCD的形状是菱形
∴ AC⊥BD,∠ABO=∠ABC=×60°=30°
在Rt△OAB中,AO=AB=×20=10
BO===
∴ 花坛的两条小路长AC=2AO=20(m)、BD=2BO=≈34.64(m)
花坛的面积S菱形ABCD=AC·BD=≈346.4(m2)
设计意图:引入实际生活案例,让学生运用所学菱形知识解决实际问题,感受数学知识在生活中的广泛应用,增强学生的数学应用意识与解决实际问题的能力,体会数学的实用价值。
(四)“智慧大闯关”—— 练习巩固
练习
1.四边形ABCD是菱形,对角线AC,BD相交于点O,且AB=5,AO=4.求AC和BD的长.
解:∵ 四边形ABCD是菱形
∴ AC⊥BD,BD=2OB,AC=2AO=8
在Rt△AOB中,OB===3
∴ BD=6
2.已知菱形的两对角线的长分别是6和8,求菱形的周长和面积.
解:∵ 四边形ABCD是菱形,且AC=8,BD=6
∴ AC⊥BD,AO=AC=4,BO=BD=3
在Rt△AOB中,AB===5
∴ C菱形ABCD=4×5=20
S菱形ABCD=×6×8=24
设计意图:通过多样化的练习题,巩固学生对菱形性质与面积公式的掌握程度,强化学生的解题技巧与运算能力,及时反馈学生的学习情况,便于教师进行针对性指导,同时以 “闯关” 形式增加练习的趣味性与挑战性,激发学生的学习积极性。
(五)“知识行囊大整理”—— 课堂小结
引导学生回顾本节课所学,分享收获。
鼓励学生提出尚未解决的问题。
设计意图:帮助学生梳理本节课的知识体系,强化重点内容,加深学生对知识的整体把握。同时,通过学生分享与提问,促进学生之间的交流与互动,培养学生的反思总结能力与问题意识,让学生学会自主学习。
四、教学总结
在本次《菱形的性质》教学旅程中,我们一同从平行四边形的旧知出发,踏上探索菱形这片新知识领域的征程。同学们积极参与动手操作,用自己的双手剪出了菱形的奥秘;在热烈的讨论与严谨的证明中,我们揭开了菱形神秘的面纱,发现了它独特的性质与美丽的面积公式。在解决生活中菱形花坛问题时,同学们更是展现出了将知识学以致用的能力。每一次思考、每一次回答问题,都是你们成长的足迹。希望同学们能将这份对数学的探索热情延续下去,在未来的数学学习中,继续发现更多的精彩与奥秘,用数学的眼光去观察世界,用数学的思维去解决问题,在数学的海洋里畅游得更远、更稳。
五、教学反思
成功之处:
教学方法上,充分利用动手操作活动,如折纸剪纸,极大地激发了学生的学习兴趣与主动性,让学生在实践中直观感受数学知识的形成过程,符合学生的认知规律,多数学生能积极参与并有所收获。
注重知识的关联性与逻辑性,通过复习平行四边形和矩形知识引入菱形,在探索菱形性质过程中不断对比与平行四边形的异同,帮助学生构建完整的知识体系,加深对知识的理解与记忆。
引入生活实例进行例题讲解,让学生切实体会到数学知识的实用性,增强了学生的数学应用意识,提高了学生解决实际问题的能力,课堂上学生对这类问题表现出较高的关注度与参与度。
不足之处:
在探索菱形性质环节,虽然大部分学生能积极参与,但仍有少数学生参与度不高,可能是操作活动的引导不够细致,未能充分考虑到不同层次学生的需求,导致部分学生在操作过程中遇到困难,影响了后续的思考与探索。
在证明菱形性质时,部分学生对证明思路的理解存在困难,反映出在逻辑推理教学方面,可能讲解速度过快,未能充分关注学生的思维节奏,需要进一步优化教学方法,给予学生更多思考与消化的时间。
改进措施:
在今后的教学中,针对操作活动,提前做好更充分的准备,如提供更详细的操作指南或进行示范,在活动过程中加强对学生的巡视与个别指导,确保每个学生都能顺利参与操作,从活动中有所收获。
在逻辑推理教学方面,放慢教学节奏,采用更多启发式提问,引导学生逐步理清证明思路,鼓励学生自主表达证明过程,及时纠正学生的错误,加强对学生逻辑思维能力的培养。同时,增加一些针对性的证明练习,让学生在实践中不断提高逻辑推理能力。
六、展示评价
评价维度 评价要点 评价等级(A. 优秀 B. 良好 C. 合格 D. 待提高)
学生参与度 是否积极参与课堂讨论、回答问题,主动参与探究活动
知识掌握 能否准确理解平行四边形对角线互相平分的性质,熟练运用性质进行证明和计算
思维能力 在观察、猜想、证明过程中,思维的敏捷性、逻辑性和创新性表现如何
合作交流 小组合作中,与小组成员沟通是否顺畅,能否积极贡献自己的想法,倾听他人意见
