湘教版九年级上期第四章锐角三角函数试题(无答案)
文档属性
| 名称 | 湘教版九年级上期第四章锐角三角函数试题(无答案) |  | |
| 格式 | rar | ||
| 文件大小 | 38.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-05 20:25:00 | ||
图片预览

文档简介
湘教版九年级上期第四章锐角三角函数试题
学校 班级 姓名 学号
一、 填空(3′×12)
1. 在Rt△ABC中,∠C=90°,a=2,b=3,则sinB= ,tanB= .
2. 在△ABC中,∠C=90°,若cosA=,则tanB=______.
3. △ABC中,若sinA=,tanB=,则∠C=_______.
4. 一等腰三角形的两边长分别为4cm和6cm,则其底角的余弦值为________.
5. 在△ABC中,若BC=,AB=,AC=3,则cosA=________.
6. 在△ABC中,AB=2,AC=,∠B=30°,则∠A=______.
7. 在Rt△ABC中,∠C=90°,面积为24cm2,b=6cm, 则sinA= .
8. 某人沿着坡度i=1:的山坡走了50米,则他离地面 米高。
9. 在△ABC中,∠C=90°,cosA=,AB=8cm ,则△ABC的面积为______。
10. 计算2sin30°+2cos60°+3tan45°=_______.
11. 已知锐角α,且sin28°=cosα,则α=________.
12.一圆柱形玻璃杯高8cm,将一根筷子插入其中,杯外最长4厘米,最短2厘米,那么这只玻璃杯的内径是________厘米.
二、 选择题(3′×12)
13. 在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值 ( )
A 也扩大3倍 B 缩小为原来的 C 都不变 D 有的扩大,有的缩小
14. 以直角坐标系的原点O为圆心,以1为半径作圆。若点P是该圆上第一象限内的一点,且OP与x轴正方向组成的角为α,则点P的坐标为 ( )
A (cosα,1) B (1,sinα) C (sinα,cosα) D (cosα,sinα)
15. 如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连结BD,若cos∠BDC=,则BC的长是 ( )
A、4cm B、6cm C、8cm D、10cm
16. 若tan(a+10°)=,则锐角a的度数是 ( )
A、20° B、30° C、35° D、50°
17. 小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30 角,且此时测得1米杆的影长为2米,则电线杆的高度为 ( )
A.9米 B.28米 C.米 D.米
18. 在Rt△ABC中,∠C=90°,当已知∠A和a时,求c,
应选择的关系式是( )
A.c= B.c= C.c=a·tanA D.c=a·cotA
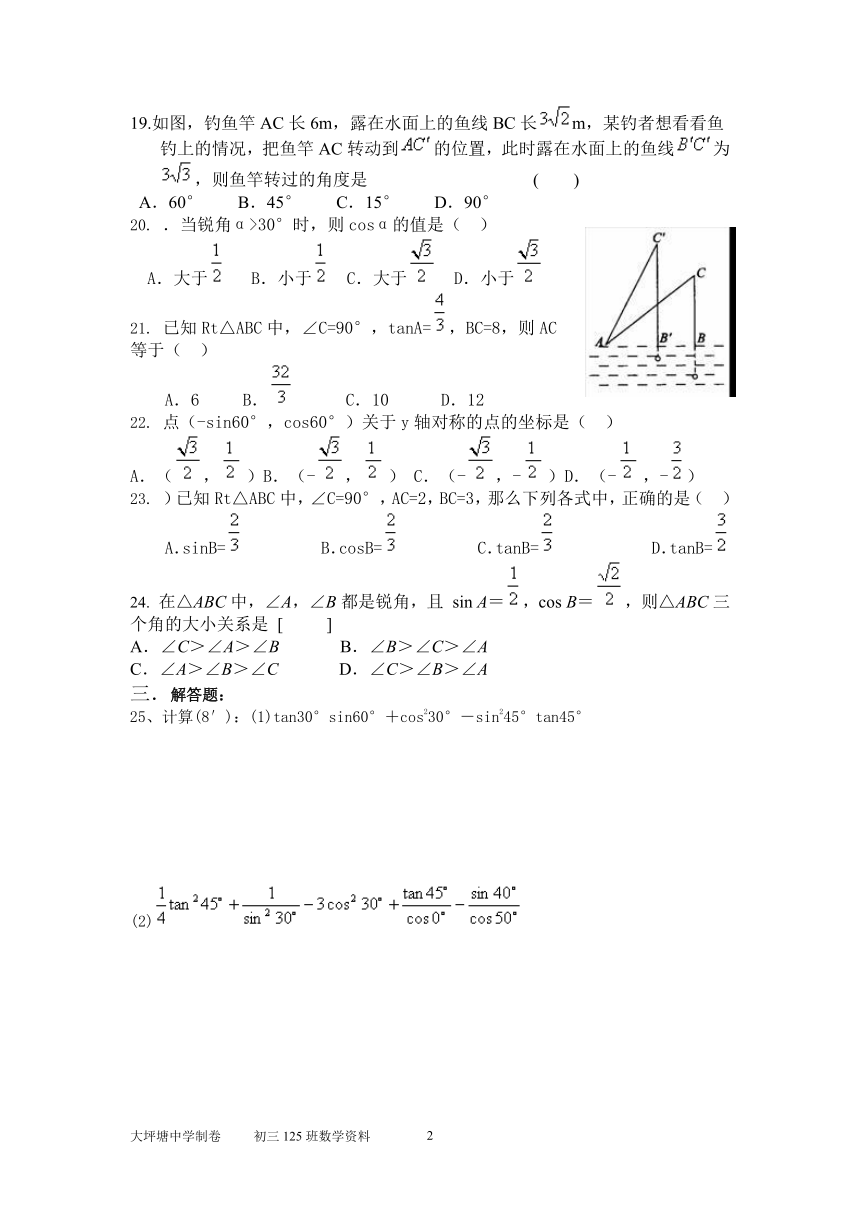
19.如图,钓鱼竿AC长6m,露在水面上的鱼线BC长m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到的位置,此时露在水面上的鱼线为,则鱼竿转过的角度是 ( )
A.60° B.45° C.15° D.90°
20. .当锐角α>30°时,则cosα的值是( )
A.大于 B.小于 C.大于 D.小于
21. 已知Rt△ABC中,∠C=90°,tanA=,BC=8,则AC等于( )
A.6 B. C.10 D.12
22. 点(-sin60°,cos60°)关于y轴对称的点的坐标是( )
A.(,)B.(-,) C.(-,-)D.(-,-)
23. )已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中,正确的是( )
A.sinB= B.cosB= C.tanB= D.tanB=
24. 在△ABC中,∠A,∠B都是锐角,且 sin A=,cos B=,则△ABC三个角的大小关系是 [ ]
A.∠C>∠A>∠B B.∠B>∠C>∠A
C.∠A>∠B>∠C D.∠C>∠B>∠A
三.解答题:
25、计算(8′):(1)tan30°sin60°+cos230°-sin245°tan45°
(2)
26.(8′)△ABC中,∠C=90°已知:c= 8,∠A=60°,求∠B、a、b.
27.(8′)如图,直升飞机在跨河大桥AB的上方点P处,此时飞机离地面的高度PO=450 m,且A,B,O三点在一条直线上,测得∠=30°,∠=45°,求大桥AB的长(结果精确到0.01 m).
28.(8′) 如图所示,在△ABC中,∠C=30°,∠BAC=105°,AD⊥BC,垂足为D,AC=20cm,求BC的长。
29.(8′) 如图,某同学用一个有60°角的直角三角板估测学校旗杆AB的高度,他将60°角的直角边水平放在1.5米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为5m,求旗杆AB的高度约为多少米(精确到1m,取1.732)
30.(8′)城市规划期间,欲拆除一电线杆AB,已知距电线杆AB水平距离14m的D处有一大坝,背水坡CD的坡度i=2:1,坝高CF为2m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道.试问:在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域.)(≈1.732,≈1.414)
PAGE
1
大坪塘中学制卷 初三125班数学资料
学校 班级 姓名 学号
一、 填空(3′×12)
1. 在Rt△ABC中,∠C=90°,a=2,b=3,则sinB= ,tanB= .
2. 在△ABC中,∠C=90°,若cosA=,则tanB=______.
3. △ABC中,若sinA=,tanB=,则∠C=_______.
4. 一等腰三角形的两边长分别为4cm和6cm,则其底角的余弦值为________.
5. 在△ABC中,若BC=,AB=,AC=3,则cosA=________.
6. 在△ABC中,AB=2,AC=,∠B=30°,则∠A=______.
7. 在Rt△ABC中,∠C=90°,面积为24cm2,b=6cm, 则sinA= .
8. 某人沿着坡度i=1:的山坡走了50米,则他离地面 米高。
9. 在△ABC中,∠C=90°,cosA=,AB=8cm ,则△ABC的面积为______。
10. 计算2sin30°+2cos60°+3tan45°=_______.
11. 已知锐角α,且sin28°=cosα,则α=________.
12.一圆柱形玻璃杯高8cm,将一根筷子插入其中,杯外最长4厘米,最短2厘米,那么这只玻璃杯的内径是________厘米.
二、 选择题(3′×12)
13. 在直角三角形中,各边的长度都扩大3倍,则锐角A的三角函数值 ( )
A 也扩大3倍 B 缩小为原来的 C 都不变 D 有的扩大,有的缩小
14. 以直角坐标系的原点O为圆心,以1为半径作圆。若点P是该圆上第一象限内的一点,且OP与x轴正方向组成的角为α,则点P的坐标为 ( )
A (cosα,1) B (1,sinα) C (sinα,cosα) D (cosα,sinα)
15. 如图,在△ABC中,∠C=90°,AC=8cm,AB的垂直平分线MN交AC于D,连结BD,若cos∠BDC=,则BC的长是 ( )
A、4cm B、6cm C、8cm D、10cm
16. 若tan(a+10°)=,则锐角a的度数是 ( )
A、20° B、30° C、35° D、50°
17. 小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30 角,且此时测得1米杆的影长为2米,则电线杆的高度为 ( )
A.9米 B.28米 C.米 D.米
18. 在Rt△ABC中,∠C=90°,当已知∠A和a时,求c,
应选择的关系式是( )
A.c= B.c= C.c=a·tanA D.c=a·cotA
19.如图,钓鱼竿AC长6m,露在水面上的鱼线BC长m,某钓者想看看鱼钓上的情况,把鱼竿AC转动到的位置,此时露在水面上的鱼线为,则鱼竿转过的角度是 ( )
A.60° B.45° C.15° D.90°
20. .当锐角α>30°时,则cosα的值是( )
A.大于 B.小于 C.大于 D.小于
21. 已知Rt△ABC中,∠C=90°,tanA=,BC=8,则AC等于( )
A.6 B. C.10 D.12
22. 点(-sin60°,cos60°)关于y轴对称的点的坐标是( )
A.(,)B.(-,) C.(-,-)D.(-,-)
23. )已知Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式中,正确的是( )
A.sinB= B.cosB= C.tanB= D.tanB=
24. 在△ABC中,∠A,∠B都是锐角,且 sin A=,cos B=,则△ABC三个角的大小关系是 [ ]
A.∠C>∠A>∠B B.∠B>∠C>∠A
C.∠A>∠B>∠C D.∠C>∠B>∠A
三.解答题:
25、计算(8′):(1)tan30°sin60°+cos230°-sin245°tan45°
(2)
26.(8′)△ABC中,∠C=90°已知:c= 8,∠A=60°,求∠B、a、b.
27.(8′)如图,直升飞机在跨河大桥AB的上方点P处,此时飞机离地面的高度PO=450 m,且A,B,O三点在一条直线上,测得∠=30°,∠=45°,求大桥AB的长(结果精确到0.01 m).
28.(8′) 如图所示,在△ABC中,∠C=30°,∠BAC=105°,AD⊥BC,垂足为D,AC=20cm,求BC的长。
29.(8′) 如图,某同学用一个有60°角的直角三角板估测学校旗杆AB的高度,他将60°角的直角边水平放在1.5米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为5m,求旗杆AB的高度约为多少米(精确到1m,取1.732)
30.(8′)城市规划期间,欲拆除一电线杆AB,已知距电线杆AB水平距离14m的D处有一大坝,背水坡CD的坡度i=2:1,坝高CF为2m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2m的人行道.试问:在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域.)(≈1.732,≈1.414)
PAGE
1
大坪塘中学制卷 初三125班数学资料
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
