第5课时 圆柱的体积课件(共25张PPT)北师大版六年级下册数学
文档属性
| 名称 | 第5课时 圆柱的体积课件(共25张PPT)北师大版六年级下册数学 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-24 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
圆柱的体积(1)
北师版·六年级下册
经历“类比猜想验证说明”来探索圆柱体积计算方法的过程,渗透转化的思想方法。
借助观察、演示、操作,建立空间观念,概括的思维能力。
感受数学与生活的联系,感悟数学知识的内在联系,激发学习兴趣。
重难点:推导圆柱体积计算公式的过程。
创新点:把课堂还给学生,动态生成。
a
b
h
a
a
a
S
S
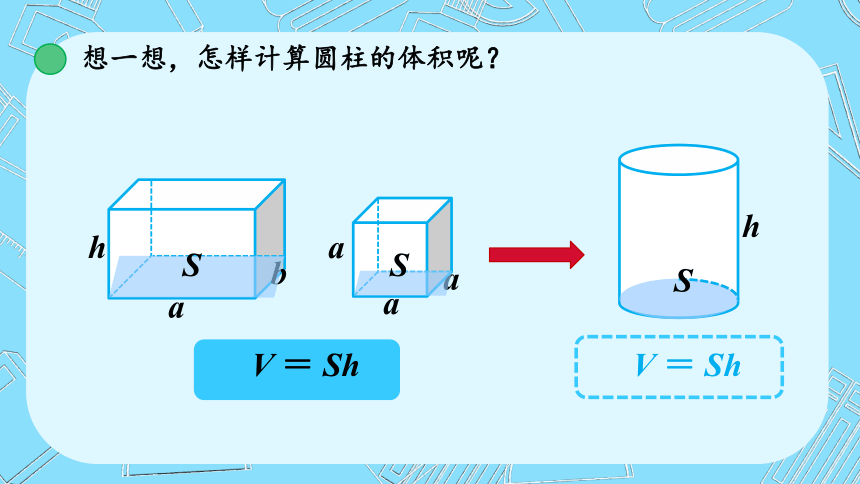
V = Sh
V = Sh
想一想,怎样计算圆柱的体积呢?
S
h
a
b
h
a
a
a
S
S
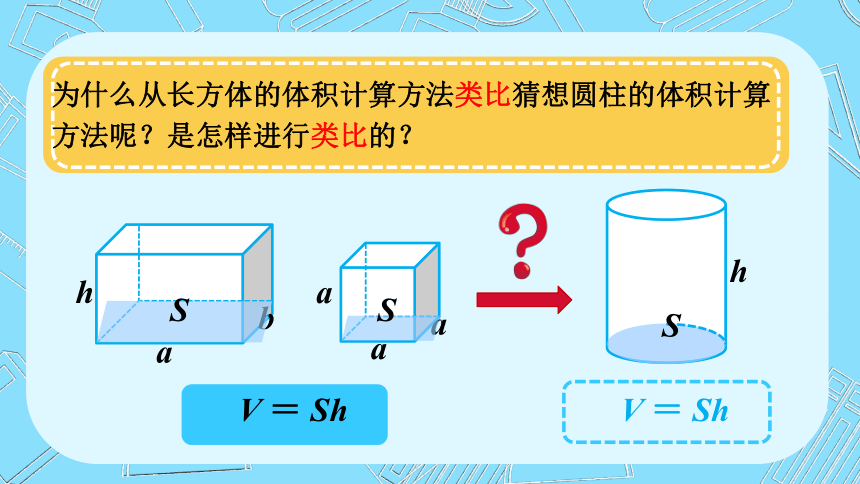
V = Sh
V = Sh
S
h
为什么从长方体的体积计算方法类比猜想圆柱的体积计算方法呢?是怎样进行类比的?
通过叠硬币,我们发现硬币的( )是固定的,每增加一枚硬币,( )就增加一些,( )也随之增大,由此可见,圆柱的体积=( )×( )。
底面积
高
体积
底面积
高
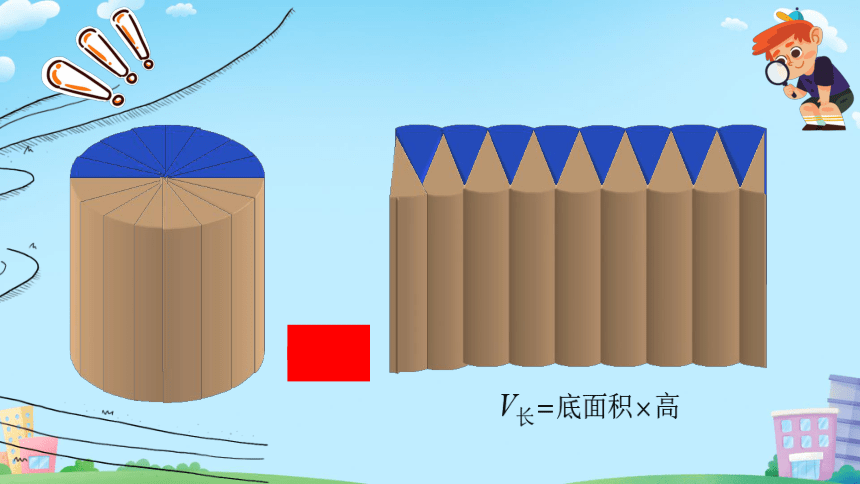
把圆柱底面等分切开后拼成一个近似的长方体
用学具来做一做,把圆柱转化为近似的长方体。
圆柱的体积
尝试验证你的猜想,并与同伴交流。
底面积
高
圆柱底面积
长方体底面积
长方体的高=h
圆柱的高
=
×
长=πr
宽=r
讨论:
V =π(d÷2)2h
V = πr2h
V =π(C÷π÷2)2h
(1)已知圆的半径r和高h,怎样求圆柱的体积?
(2)已知圆的直径d和高h,怎样求圆柱的体积?
(3)已知圆的周长C和高h,怎样求圆柱的体积?
圆柱的体积
底面积
高
=
×
V = Sh
V =π(d÷2)2h
V = πr2h
V =π(C÷π÷2)2h
圆柱的侧面积 = 底面周长 × 高
S侧 = Ch
S侧 = 2πrh
S侧 = πdh
38π㎝
10㎝
16㎝
5㎝
甲圆柱与乙圆柱谁的体积大?
它们的什么条件是相同的?
圆柱的体积大小与什么有关?
想一想
高相等时底面积越大的体积越大。
想一想
当底面积相等时,高越长的体积越大。
将一个圆柱截成不相等的两段,哪个圆柱体积大?
尝试解决下面的问题,并与同伴交流。
笑笑了解到一根柱子的底面半径为0.4m,高为5m。你能算出它的体积吗?
V = πr2h
V = πr2h =3.14×0.42×5
=3.14×0.16×5
=3.14×0.8
=2.512(m3)
答:需要2.512m3木材。
r=0.4m
尝试解决下面的问题,并与同伴交流。
从水杯里面量,水杯的底面直径是6 cm,高是16 cm,这个水杯能装多少毫升水?
V = π(d÷2)2h
V=πr2h=3.14×32×16
=3.14×9×16
=452.16(cm3)
=452.16(毫升)
答:这个杯子能装452.16毫升水。
水杯能装水的体积就是水杯的容积。
r=d÷2=6÷2=3(cm)
1.分别计算下列各图形的体积,再说说这几个图形体积计算
方法之间的联系。
4×3×8
=96(cm3)
6×6×6
=216(cm3)
3.14×2.52×8
=157(cm3)
V = Sh
【选自教材P9 练一练 第1题】
r=d÷2=5÷2=2.5(cm)
2.计算下面各圆柱的体积。
60×4
=240(cm3)
3.14×12×5
=15.7(cm3)
3.14×32×10
=282.6(dm3)
V = Sh
V = πr2h
V = π(d÷2)2h
【选自教材P9 练一练 第2题】
r=1cm
r=d÷2=6÷2=3(cm)
3.这个杯子能否装下3000mL的牛奶?
V=3.14×72×20
=3077.2(cm3)
=3077.2(mL)
3077.2mL>3000mL
答:这个杯子能装下3000mL的牛奶。
V = πr2h
r=d÷2=14÷2=7(cm)
谢 谢
圆柱的体积(1)
北师版·六年级下册
经历“类比猜想验证说明”来探索圆柱体积计算方法的过程,渗透转化的思想方法。
借助观察、演示、操作,建立空间观念,概括的思维能力。
感受数学与生活的联系,感悟数学知识的内在联系,激发学习兴趣。
重难点:推导圆柱体积计算公式的过程。
创新点:把课堂还给学生,动态生成。
a
b
h
a
a
a
S
S
V = Sh
V = Sh
想一想,怎样计算圆柱的体积呢?
S
h
a
b
h
a
a
a
S
S
V = Sh
V = Sh
S
h
为什么从长方体的体积计算方法类比猜想圆柱的体积计算方法呢?是怎样进行类比的?
通过叠硬币,我们发现硬币的( )是固定的,每增加一枚硬币,( )就增加一些,( )也随之增大,由此可见,圆柱的体积=( )×( )。
底面积
高
体积
底面积
高
把圆柱底面等分切开后拼成一个近似的长方体
用学具来做一做,把圆柱转化为近似的长方体。
圆柱的体积
尝试验证你的猜想,并与同伴交流。
底面积
高
圆柱底面积
长方体底面积
长方体的高=h
圆柱的高
=
×
长=πr
宽=r
讨论:
V =π(d÷2)2h
V = πr2h
V =π(C÷π÷2)2h
(1)已知圆的半径r和高h,怎样求圆柱的体积?
(2)已知圆的直径d和高h,怎样求圆柱的体积?
(3)已知圆的周长C和高h,怎样求圆柱的体积?
圆柱的体积
底面积
高
=
×
V = Sh
V =π(d÷2)2h
V = πr2h
V =π(C÷π÷2)2h
圆柱的侧面积 = 底面周长 × 高
S侧 = Ch
S侧 = 2πrh
S侧 = πdh
38π㎝
10㎝
16㎝
5㎝
甲圆柱与乙圆柱谁的体积大?
它们的什么条件是相同的?
圆柱的体积大小与什么有关?
想一想
高相等时底面积越大的体积越大。
想一想
当底面积相等时,高越长的体积越大。
将一个圆柱截成不相等的两段,哪个圆柱体积大?
尝试解决下面的问题,并与同伴交流。
笑笑了解到一根柱子的底面半径为0.4m,高为5m。你能算出它的体积吗?
V = πr2h
V = πr2h =3.14×0.42×5
=3.14×0.16×5
=3.14×0.8
=2.512(m3)
答:需要2.512m3木材。
r=0.4m
尝试解决下面的问题,并与同伴交流。
从水杯里面量,水杯的底面直径是6 cm,高是16 cm,这个水杯能装多少毫升水?
V = π(d÷2)2h
V=πr2h=3.14×32×16
=3.14×9×16
=452.16(cm3)
=452.16(毫升)
答:这个杯子能装452.16毫升水。
水杯能装水的体积就是水杯的容积。
r=d÷2=6÷2=3(cm)
1.分别计算下列各图形的体积,再说说这几个图形体积计算
方法之间的联系。
4×3×8
=96(cm3)
6×6×6
=216(cm3)
3.14×2.52×8
=157(cm3)
V = Sh
【选自教材P9 练一练 第1题】
r=d÷2=5÷2=2.5(cm)
2.计算下面各圆柱的体积。
60×4
=240(cm3)
3.14×12×5
=15.7(cm3)
3.14×32×10
=282.6(dm3)
V = Sh
V = πr2h
V = π(d÷2)2h
【选自教材P9 练一练 第2题】
r=1cm
r=d÷2=6÷2=3(cm)
3.这个杯子能否装下3000mL的牛奶?
V=3.14×72×20
=3077.2(cm3)
=3077.2(mL)
3077.2mL>3000mL
答:这个杯子能装下3000mL的牛奶。
V = πr2h
r=d÷2=14÷2=7(cm)
谢 谢
