2025年中考数学一轮复习 专题十六 图形的相似与位似 习题课件(84张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 专题十六 图形的相似与位似 习题课件(84张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 17.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-24 15:55:17 | ||
图片预览










文档简介
(共84张PPT)
专题十六 图形的相似与位似
中考数学一轮复习备考合集
考情分析
命题点 命题形式 命题热度 命题特点
相似三角形 1.比例的性质 ☆ 本专题主要以选择题、填空题和解答题的形式出现,重点考查学生利用相关定理和性质进行证明的能力,近年来更加注重利用相似解决实际问题的开放探究,体现了数形结合的核心素养
2.平行线分线段成比例 ☆ 3.相似三角形的性质 ☆☆☆ 4.相似三角形的有关证明与计算 ☆☆☆ 5.相似三角形的实际应用 ☆☆ 位似 6.位似 ☆☆
讲解一:
比例线段
知识复习
一、比例线段的相关概念及性质
1.线段的比:在同一长度单位下,量得的两条线段长度的比叫做这两条线段的比.
【注意】两条线段的比,与所选的长度单位无关,但所选的长度单位必须一致,其值是一个没有单位的正数.
知识复习
一、比例线段的相关概念及性质
知识复习
一、比例线段的相关概念及性质
3.比例的相关性质:
知识复习
一、比例线段的相关概念及性质
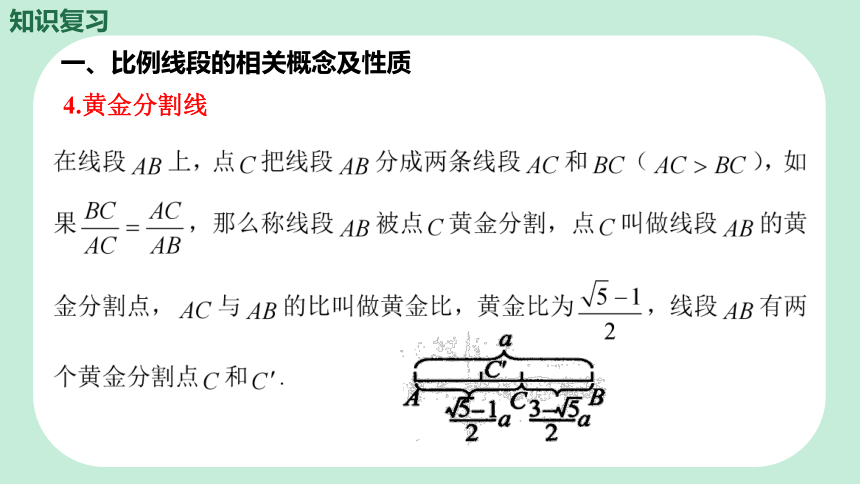
4.黄金分割线
知识复习
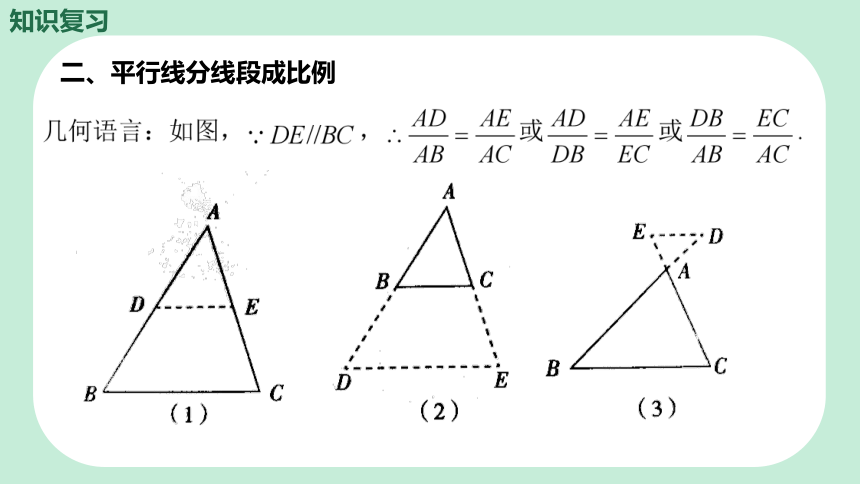
二、平行线分线段成比例
知识复习
二、平行线分线段成比例
知识复习
二、平行线分线段成比例
知识复习
二、平行线分线段成比例
命题形式1 比例的性质
A
命题形式1 比例的性质
1
命题形式1 比例的性质
2
命题形式2 平行线分线段成比例
B
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
D
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
C
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
A
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
讲解二:
三角形相似的判定与性质
知识复习
一、相似图形
相似图形:我们把形状相同的图形叫做相似图形.
【注意】
(1)两个图形是否相似与图形的大小、位置无关.
(2)两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
(3)全等图形是特殊的相似图形,也就是说全等图形一定是相似图形,但相似图形不一定是全等图形.
知识复习
二、相似多边形
1.相似多边形:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
【注意】两个多边形相似,必须同时具备三个条件:(1)边数相同;(2)角分别相等;(3)边成比例.
2.相似比:相似多边形对应边的比叫做相似比.
知识复习
二、相似多边形
3.相似多边形的性质:相似多边形的对应角相等,对应边成比例.
【注意】
(1)相似多边形的对应角相等,但相等的两个角未必是对应角,要结合图形去观察它们之间的对应关系.
(2)相似多边形的定义可用来判断两个多边是否相似.
(3)相似多边形的性质常用来求相似多边形未知边的长度或未知角的度数.
知识复习
三、相似三角形的判定
1.利用平行线判定两个三角形相似的定理
定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
知识复习
三、相似三角形的判定
2.利用两边和夹角判定两个三角形相似的定理
定理:两边成比例且夹角相等的两个三角形相似.
【注意】应用该定理判定两个三角形相似时,相等的角必须是成比例的两边的夹角.
知识复习
三、相似三角形的判定
3.应用三边判定两个三角形相似的定理:三边成比例的两个三角形相似.
【注意】利用三边成比例判定两个三角形相似时,一定要注意边与边之间的对应关系,主要根据最长边与最长边对应,最短边与最短边对应的思路找对应边.
知识复习
三、相似三角形的判定
4.利用两角判定两个三角形相似的定理:两角分别相等的两个三角形相似.
【注意】利用此定理证明两个三角形相似的关键是找相等的角.如公共角、对顶角、同角(等角)的余角(补角)、同弧所对的圆周角等都是相等的角,解题时要注意挖掘题目中的隐含条件.
知识复习
三、相似三角形的判定
5.直角三角形相似的判定方法
①一个锐角相等的两个直角三角形相似;
②两组直角边成比例的两个直角三角形相似;
③斜边和一条直角边成比例的两个直角三角形相似.
知识复习
四、相似三角形的性质
1.根据三角形相似的定义可知,相似三角形的对应角相等,对应边成比例.
知识复习
四、相似三角形的性质
知识复习
四、相似三角形的性质
知识复习
四、相似三角形的性质
知识复习
四、相似三角形的性质
知识复习
四、相似三角形的性质
【注意】
在应用相似三角形对应线段的性质解题时,要注意并不是相似三角形中任意高的比、中线的比、角平分线的比都等于相似比,而是相似三角形中对应高的比、对应中线的比、对应角平分线的比等于相似比.
3.相似三角形周长的比等于相似比.
4.相似三角形面积的比等于相似比的平方.
知识复习
四、相似三角形的性质
5.应用
知识复习
五、相似三角形的判定思路
知识复习
六、相似三角形的常见模型
知识复习
六、相似三角形的常见模型
知识复习
六、相似三角形的常见模型
知识复习
六、相似三角形的常见模型
命题形式3 相似三角形的性质
D
命题形式3 相似三角形的性质
D
命题形式3 相似三角形的性质
B
命题形式3 相似三角形的性质
1 : 2
命题形式3 相似三角形的性质
9 : 4
命题形式4 相似三角形的有关证明与计算
A
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
C
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
96
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
命题形式5 相似三角形的实际应用
D
命题形式5 相似三角形的实际应用
命题形式5 相似三角形的实际应用
命题形式5 相似三角形的实际应用
80
命题形式5 相似三角形的实际应用
命题形式5 相似三角形的实际应用
20
命题形式5 相似三角形的实际应用
命题形式5 相似三角形的实际应用
讲解三:
位似
知识复习
定义:两个图形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行(或在同一直线上),像这样的两个图形叫做位似图形,这个点叫做位似中心.
性质:(1)位似图形上的任意一对对应点到位似中心的距离的比等于相似比;
(2)位似图形对应点的连线或延长线相交于一点;
(3)位似图形对应边平行(或在同一条直线上);
(4)位似图形对应角相等;
(5)在平面直角坐标系中,如果原点为位似中心,相似比为k,那么位似图形对应点的坐标比等于±k
知识复习
作图步骤:确定位似中心;确定原图形中各顶点关于位似中心的对应点;描出新图形
基本图形:
命题形式6 位似
D
命题形式6 位似
命题形式6 位似
A
命题形式6 位似
命题形式6 位似
1 : 3
命题形式6 位似
命题形式6 位似
命题形式6 位似
我们下节课再见
See you in the next video
专题十六 图形的相似与位似
中考数学一轮复习备考合集
考情分析
命题点 命题形式 命题热度 命题特点
相似三角形 1.比例的性质 ☆ 本专题主要以选择题、填空题和解答题的形式出现,重点考查学生利用相关定理和性质进行证明的能力,近年来更加注重利用相似解决实际问题的开放探究,体现了数形结合的核心素养
2.平行线分线段成比例 ☆ 3.相似三角形的性质 ☆☆☆ 4.相似三角形的有关证明与计算 ☆☆☆ 5.相似三角形的实际应用 ☆☆ 位似 6.位似 ☆☆
讲解一:
比例线段
知识复习
一、比例线段的相关概念及性质
1.线段的比:在同一长度单位下,量得的两条线段长度的比叫做这两条线段的比.
【注意】两条线段的比,与所选的长度单位无关,但所选的长度单位必须一致,其值是一个没有单位的正数.
知识复习
一、比例线段的相关概念及性质
知识复习
一、比例线段的相关概念及性质
3.比例的相关性质:
知识复习
一、比例线段的相关概念及性质
4.黄金分割线
知识复习
二、平行线分线段成比例
知识复习
二、平行线分线段成比例
知识复习
二、平行线分线段成比例
知识复习
二、平行线分线段成比例
命题形式1 比例的性质
A
命题形式1 比例的性质
1
命题形式1 比例的性质
2
命题形式2 平行线分线段成比例
B
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
D
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
C
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
A
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
命题形式2 平行线分线段成比例
讲解二:
三角形相似的判定与性质
知识复习
一、相似图形
相似图形:我们把形状相同的图形叫做相似图形.
【注意】
(1)两个图形是否相似与图形的大小、位置无关.
(2)两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.
(3)全等图形是特殊的相似图形,也就是说全等图形一定是相似图形,但相似图形不一定是全等图形.
知识复习
二、相似多边形
1.相似多边形:两个边数相同的多边形,如果它们的角分别相等,边成比例,那么这两个多边形叫做相似多边形.
【注意】两个多边形相似,必须同时具备三个条件:(1)边数相同;(2)角分别相等;(3)边成比例.
2.相似比:相似多边形对应边的比叫做相似比.
知识复习
二、相似多边形
3.相似多边形的性质:相似多边形的对应角相等,对应边成比例.
【注意】
(1)相似多边形的对应角相等,但相等的两个角未必是对应角,要结合图形去观察它们之间的对应关系.
(2)相似多边形的定义可用来判断两个多边是否相似.
(3)相似多边形的性质常用来求相似多边形未知边的长度或未知角的度数.
知识复习
三、相似三角形的判定
1.利用平行线判定两个三角形相似的定理
定理:平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
知识复习
三、相似三角形的判定
2.利用两边和夹角判定两个三角形相似的定理
定理:两边成比例且夹角相等的两个三角形相似.
【注意】应用该定理判定两个三角形相似时,相等的角必须是成比例的两边的夹角.
知识复习
三、相似三角形的判定
3.应用三边判定两个三角形相似的定理:三边成比例的两个三角形相似.
【注意】利用三边成比例判定两个三角形相似时,一定要注意边与边之间的对应关系,主要根据最长边与最长边对应,最短边与最短边对应的思路找对应边.
知识复习
三、相似三角形的判定
4.利用两角判定两个三角形相似的定理:两角分别相等的两个三角形相似.
【注意】利用此定理证明两个三角形相似的关键是找相等的角.如公共角、对顶角、同角(等角)的余角(补角)、同弧所对的圆周角等都是相等的角,解题时要注意挖掘题目中的隐含条件.
知识复习
三、相似三角形的判定
5.直角三角形相似的判定方法
①一个锐角相等的两个直角三角形相似;
②两组直角边成比例的两个直角三角形相似;
③斜边和一条直角边成比例的两个直角三角形相似.
知识复习
四、相似三角形的性质
1.根据三角形相似的定义可知,相似三角形的对应角相等,对应边成比例.
知识复习
四、相似三角形的性质
知识复习
四、相似三角形的性质
知识复习
四、相似三角形的性质
知识复习
四、相似三角形的性质
知识复习
四、相似三角形的性质
【注意】
在应用相似三角形对应线段的性质解题时,要注意并不是相似三角形中任意高的比、中线的比、角平分线的比都等于相似比,而是相似三角形中对应高的比、对应中线的比、对应角平分线的比等于相似比.
3.相似三角形周长的比等于相似比.
4.相似三角形面积的比等于相似比的平方.
知识复习
四、相似三角形的性质
5.应用
知识复习
五、相似三角形的判定思路
知识复习
六、相似三角形的常见模型
知识复习
六、相似三角形的常见模型
知识复习
六、相似三角形的常见模型
知识复习
六、相似三角形的常见模型
命题形式3 相似三角形的性质
D
命题形式3 相似三角形的性质
D
命题形式3 相似三角形的性质
B
命题形式3 相似三角形的性质
1 : 2
命题形式3 相似三角形的性质
9 : 4
命题形式4 相似三角形的有关证明与计算
A
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
C
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
96
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
命题形式4 相似三角形的有关证明与计算
命题形式5 相似三角形的实际应用
D
命题形式5 相似三角形的实际应用
命题形式5 相似三角形的实际应用
命题形式5 相似三角形的实际应用
80
命题形式5 相似三角形的实际应用
命题形式5 相似三角形的实际应用
20
命题形式5 相似三角形的实际应用
命题形式5 相似三角形的实际应用
讲解三:
位似
知识复习
定义:两个图形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行(或在同一直线上),像这样的两个图形叫做位似图形,这个点叫做位似中心.
性质:(1)位似图形上的任意一对对应点到位似中心的距离的比等于相似比;
(2)位似图形对应点的连线或延长线相交于一点;
(3)位似图形对应边平行(或在同一条直线上);
(4)位似图形对应角相等;
(5)在平面直角坐标系中,如果原点为位似中心,相似比为k,那么位似图形对应点的坐标比等于±k
知识复习
作图步骤:确定位似中心;确定原图形中各顶点关于位似中心的对应点;描出新图形
基本图形:
命题形式6 位似
D
命题形式6 位似
命题形式6 位似
A
命题形式6 位似
命题形式6 位似
1 : 3
命题形式6 位似
命题形式6 位似
命题形式6 位似
我们下节课再见
See you in the next video
同课章节目录
