2008-2009学年度第二学期期末教学质量检测九年级数学试卷
文档属性
| 名称 | 2008-2009学年度第二学期期末教学质量检测九年级数学试卷 |  | |
| 格式 | rar | ||
| 文件大小 | 102.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-04 10:14:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
九年级数学模拟试卷
作者:迁安旭阳学校 王书新
本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.
本试卷满分为120分,考试时间为120分钟.
卷Ⅰ(选择题,共20分)
一、选择题(本大题共12个小题;每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.的相反数是(原创)( )
A. B. C.2 D.
2.北京2008奥运的国家体育场“鸟巢” 建筑面积达25.8万平方米, 用科学记数法表示应为( 摘自2008河北省中考模拟试卷)
A. B. C. D.
3.函数的自变量的取值范围在数轴上可表示为(原创) ( )
4.下列运算中,结果正确的是(原创) ( )
A. B.
C. D.
5.已知点A(,1)在双曲线上,则m的值为(原创) ( )
A.-5 B.-3 C.1 D.2
6.家家乐奥运福娃专卖店今年3月份售出福娃3600个,5月份售出4900个,设每月平均增长率为x,下面所列方程正确的是(根据2008河北省中考试题改编) ( )
A.3600x2=4900 B.3600(1+x)2=4900
C.3600(1+x%)2=4900 D.3600(1+ x)+3600(1+x)2=4900
7.甲、乙、丙三个同学排成一排拍照,则甲排在中间的概率是( 原创) ( )
A. B. C. D.
8.已知,⊙O的半径为4cm,点P是⊙O内一点,OP=2cm.以P为圆心作一个圆与⊙O相切,则这个圆的半径为( 学习点津与能力测评P206改编 ) ( )
A.2cm B.2cm或6cm C.6cm D.以上答案均不对
9.已知代数式的值为9,则的值为 ( ) ( 原创)
A.7 B.9 C.12 D.18
10.如图,直线l是一条河,P、Q两地相距8千米,P、Q两地到l的距离分别为2千米、5千米,欲在l上的某点M处修建一个水泵站,向P、Q两地供水,以下四种铺设方案(图中实线表示铺设的管道)铺设的管道最短的是(根据2008河北中考题改编) ( )
九年级数学模拟试卷
卷II(非选择题,共100分)
注意事项:1.答卷II前,将密封线左侧的项目填写清楚.
2.答卷II时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.
二、填空题(本大题共6个小题;每小题3分,共18分.把答案写在题中横线上)
13.单项式的系数是 .(原创)
14. 化简的结果是 .(原创)
15.如图,在中,分别是的中点,若,则 cm.(原创)
16.已知x、y满足方程组则x-y的值为 .(原创)
17.如图,AO为入射光线,OB为反射光线.已知A(-2, 3),由光的反射原理:入射角等于反射角,得到OB所在直线的解析式为 .(摘自2008河北省模拟试卷)
18.如图,在中,,于,若,,则= .(原创)
三、解答题(本大题共8个小题;共78分.解答应写出文字说明、证明过程或演算步骤)
19.(本小题满分8分)(原创)
已知,求的值.
20.(本小题满分8分)(根据2007江西省中考试题改编)
某校为研究学生的课余爱好情况,采取抽样的方法,从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制了如下的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了 名学生,计算四个方面爱好人数的极差;
(2)补全频数分布折线图;
(3)若该校共1500名学生,估计全校爱好运动的学生有多少 名;
(4)在全校同学中随机选出一名学生参加演讲比赛,选出的恰好是爱好阅读的学生的概率是 .
21.(本小题满分10分)((根据2008河北省中考试卷改编)
已知:如图△ABC内接于⊙O,于H,过A点的切线与OC的延长线交于点D,°,.请求出:
(1)线段AC的长;
(2)劣弧AC的长(结果保留);
(3)线段AD的长.
22.(本小题满分10分)((根据2008河北省中考试卷改编))
阅读理解
对于任意正实数,,,
,只有当时,等号成立.
结论:在(均为正实数)中,若为定值,则,只有当时,有最小值.
根据上述内容,回答下列问题:
若,只有当 时,有最小值 .
思考验证
如图,为半圆的直径,为半圆上任意一点,(与点不重合).过点作,垂足为,,.
试根据图形验证,并指出等号成立时的条件.
探索应用
已知x>0,求代数式的最小值,并说明等号成立的条件.
23.(本小题满分10分)(模仿2007河北省中考试卷)
如图,已知抛物线经过点A、B、C,顶点为点D,与x轴的另一交点为E.
(1)求抛物线的解析式及顶点坐标;
(2)求四边形ABDE的面积;
(3)求抛物线顶点D关于x轴对称的点D'的坐标,并判断四边形ADE D'是何特殊四边形.(不要求说明理由)
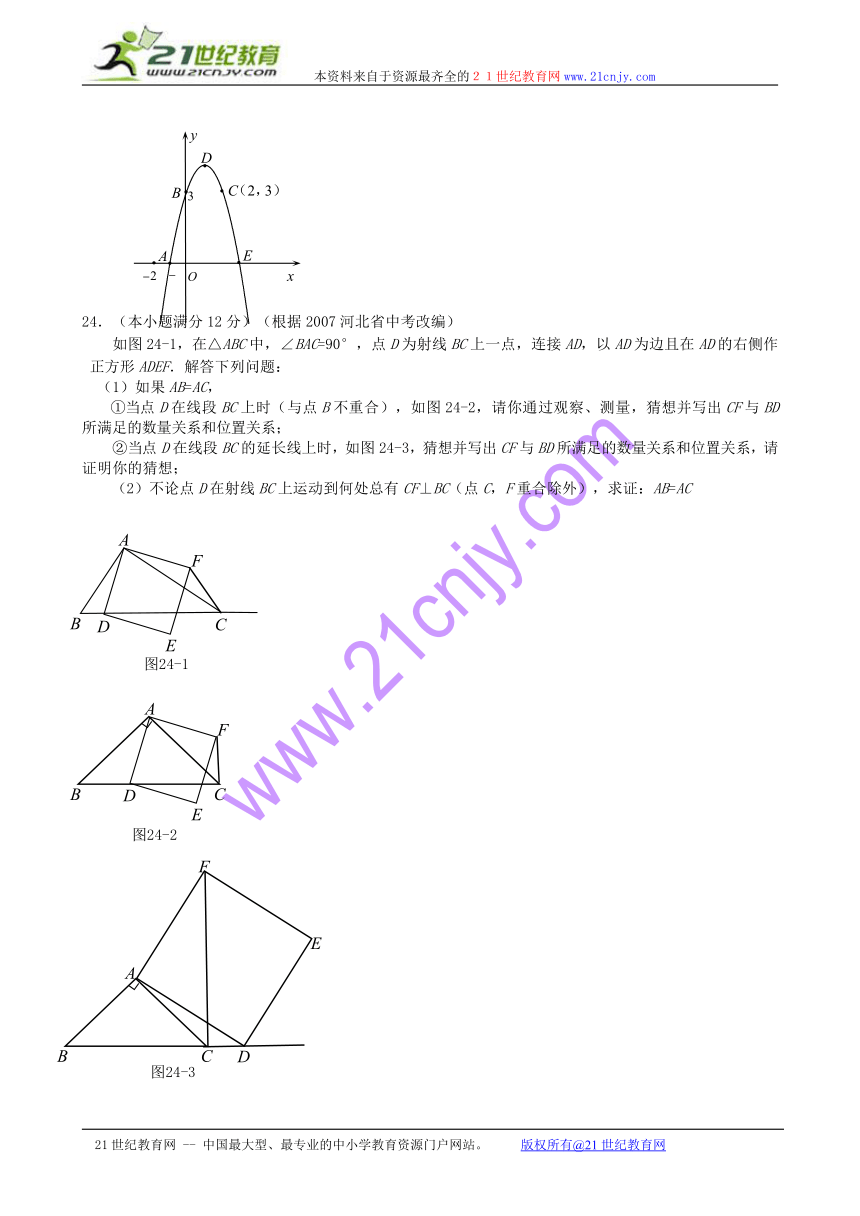
24.(本小题满分12分)(根据2007河北省中考改编)
如图24-1,在△ABC中,∠BAC=90°,点D为射线BC上一点,连接AD,以AD为边且在AD的右侧作正方形ADEF.解答下列问题:
(1)如果AB=AC,
①当点D在线段BC上时(与点B不重合),如图24-2,请你通过观察、测量,猜想并写出CF与BD所满足的数量关系和位置关系;
②当点D在线段BC的延长线上时,如图24-3,猜想并写出CF与BD所满足的数量关系和位置关系,请证明你的猜想;
(2)不论点D在射线BC上运动到何处总有CF⊥BC(点C,F重合除外),求证:AB=AC
25.本小题满分12分(根据2007河北省中考改编)
某工程机械厂根据市场需求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:
型号 A B
成本(万元/台) 200 240
售价(万元/台) 250 300
设生产A型挖掘机x台
(1)求该厂对这两型挖掘机有哪几种生产方案?
(2))设该厂出售挖掘机获得利润W万元,求该厂如何生产能获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂应该如何生产可以获得最大利润?(注:利润=售价-成本)
26.(本小题满分12分)(摘自2008河北省中考模拟试卷)
如图,Rt△ABC中,∠B=90°,∠CAB=30°.它的顶点A的坐标为(10,0),顶点B的坐标为(5,),AB=10,点P从点A出发,沿折线A→B→C以2个单位/秒的速度运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
(1)求∠BAO的度数及运动2秒时△OPQ的面积;
(2)当点P在AB上运动,求t为何值时,?
(3)当点P在AB上运动时,求△OPQ的面积S(平方单位)与时间t(秒)之间的函数关系式(不要求写出函数的自变量取值范围)及面积S取最大值时点P的坐标;
(4)点P沿AB边运动时,∠OPQ的大小随着时间t的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间t的增大而减小.当点P沿这两边运动时,使∠OPQ=90°的点P有几个?请通过画图、测量等方法得出结果,并说明理由.
九年级数学模拟试卷答案
一、选择题(每小题2分,共24分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案 C C B D A C B A A B
二、填空题(每小题3分,共18分)
13. 14.3 15.4 16.1 17. 18.
三、解答题(本大题共8个小题;共78分)
19.解:原式=……………………………………………………4分
=…………………………………………………………………5分
当x=时,原式=4.……………………………………………………8分
(注:本题若直接代入求值,结果正确也相应给分)
20.解:(1)100……………………………………………………………………1分
因为爱好阅读学生为100×30%=30名,爱好其它学生为10名,由图可知爱好运动和娱乐学生分别为40和20名,所以四个方面爱好人数的极差为40-10=30名;………………………………………………………………………………………3分
()图略……………………………………………………………………………5分
(3)600……………………………………………………………………………6分
(4)……………………………………………………………………………8分
21.解:(1)连结OA,
……………………………………………………………1分
,OH =5 ∴AC=2AH=2·OH·= ……………………4分
(2)OA=OC=AC
∴劣弧AC的长=
∴劣弧AC的长是…………………………………………………………7分
(3) ∵AD是切线 ∴ ……………………………………………8分
∵ ∴AD=·OA=10
∴线段AD的长是10…………………………………………………………………10分
22.阅读理解:1(写不扣分),2…………………………………………4分
思考验证:AB是直径,……………………………………………5分
又
~ …………………………………………………………6分
CD=
若点D与O不重合,连接OC,在中,OC>CD>
若点D与O重合,OC=CD=
综上所述,≥即,当CD等于半径时,等号成立……7分
探索应用:=
x>0≥即≥6
有最小值6,此时有最小值12
只有当时,即时,等号成立……………………………………………10分
23.(1)设抛物线的解析式为……………………………1分
抛物线经过点A、B、C
抛物线的解析式为,…………………………………………3分
顶点D(1,4)………………………………………………………………………5分
(2)E(3,0)………………………………………………………………………6分
==9…………8分
(3)D'(1,-4)
四边形ADE D'是菱形………………………………………………………………10分
24.(1)①CF=BD,CF⊥BD………………………………………………………2分
②CF=BD,CF⊥BD…………………………………………………………………4分
证明:∵ABCD为正方形∴∠DAF=∠BAC=90°∴∠BAD=∠CAF
∵AD=AF,AB=AC∴△ABD≌△ACF,……………………………………………7分
∴CF=BD,∠ACF=∠B=45°
∴∠BCF=90°即CF⊥BD…………………………………………………………8分
(2)将(1)的证明过程逆过来 …………………………………………………12分
25.解 :(1)设生产A型挖掘机x台,则B型挖掘机可生产(100-x)台,………1分
由题意知 ,…………………………………3分
解得37.5≤x≤40…………………………………………………………………4分
∵x取非负整数,∴x为38,39,40∴有三种生产方案:A型38台,B型62台;A型39台,B型61台;A型40台,B型60台.………………………………………………………5分
(2)设获得利润W万元,由题意知W=50x+60(100-x)=6000-10 x………………7分
∴当x=38时,W最大=5620万元,即生产A型38台,B型62台获得利润最大.………9分
(3)由题意知W=(50+m)x+60(100-x)=6000+( m -10) x……………………10分
∴当0当m=10时,m -10=0,三种生产方案获得利润相等;
当m>10时,则x=40时,W最大,即生产A型40台,B型60台.……………12分
26.解:(1)∠BAO =60°;运动2秒时,OQ=2+4=6,AP=4,点P的横坐标是10-=8,
所以此时△OPQ的面积=;……………………………………… 4分
(2)2.5秒
(3)点P在AB上运动时,OQ=2+2t,AP=2t,点P的横坐标是10-=10-t,
∴=.……………………………………………6分
∴当时,面积S最大.…………………………………………7分
这时点P的横坐标是10-t=;
点P的纵坐标是=.
即P(,); …………………………………………………………9分
(4)当点沿这两边运动时,使∠OPQ=90°的点P有2个.…………………11分
当点P与点A重合时,∠OPQ<90°,当点P运动到与点B重合时,画图(或测量) 知,∠OPQ>90°.所以当点P在AB边上运动时,使∠OPQ=90°的点P有1个.同理当点P运动到与点C重合时, ∠OPQ<90°,所以当点P在BC边上运动时,使∠OPQ=90°的点P也有1个.当点沿这两边运动时,使∠OPQ=90°的点P有2个.………………………………………………………………………………12分
1
0
A
x
1
0
B
x
1
0
C
x
1
0
D
x
P
M
M
M
M
Q
l
l
l
l
P
Q
P
Q
P
Q
P
Q
A
B
C
D
(第12题)
l
B
y
A
(第17题)
O
A
C
B
D
(第18题)
C
A
E
D
B
(第15题)
x
运动
娱乐
阅读
其它
项目
10
20
30
40
50
人数
O
图20-1
其它
运动
30%
娱乐
20%
阅读
图20-2
O
A
D
B
C
H
A
O
D
B
C
x
y
O
3
-
-2
A
B
D
E
C(2,3)
B
F
E
D
C
A
图24-2
B
F
E
D
C
A
图24-1
B
F
D
C
A
图24-3
E
O
A
C
B
P
Q
D
x
y
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
九年级数学模拟试卷
作者:迁安旭阳学校 王书新
本试卷分卷Ⅰ和卷Ⅱ两部分;卷Ⅰ为选择题,卷Ⅱ为非选择题.
本试卷满分为120分,考试时间为120分钟.
卷Ⅰ(选择题,共20分)
一、选择题(本大题共12个小题;每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.的相反数是(原创)( )
A. B. C.2 D.
2.北京2008奥运的国家体育场“鸟巢” 建筑面积达25.8万平方米, 用科学记数法表示应为( 摘自2008河北省中考模拟试卷)
A. B. C. D.
3.函数的自变量的取值范围在数轴上可表示为(原创) ( )
4.下列运算中,结果正确的是(原创) ( )
A. B.
C. D.
5.已知点A(,1)在双曲线上,则m的值为(原创) ( )
A.-5 B.-3 C.1 D.2
6.家家乐奥运福娃专卖店今年3月份售出福娃3600个,5月份售出4900个,设每月平均增长率为x,下面所列方程正确的是(根据2008河北省中考试题改编) ( )
A.3600x2=4900 B.3600(1+x)2=4900
C.3600(1+x%)2=4900 D.3600(1+ x)+3600(1+x)2=4900
7.甲、乙、丙三个同学排成一排拍照,则甲排在中间的概率是( 原创) ( )
A. B. C. D.
8.已知,⊙O的半径为4cm,点P是⊙O内一点,OP=2cm.以P为圆心作一个圆与⊙O相切,则这个圆的半径为( 学习点津与能力测评P206改编 ) ( )
A.2cm B.2cm或6cm C.6cm D.以上答案均不对
9.已知代数式的值为9,则的值为 ( ) ( 原创)
A.7 B.9 C.12 D.18
10.如图,直线l是一条河,P、Q两地相距8千米,P、Q两地到l的距离分别为2千米、5千米,欲在l上的某点M处修建一个水泵站,向P、Q两地供水,以下四种铺设方案(图中实线表示铺设的管道)铺设的管道最短的是(根据2008河北中考题改编) ( )
九年级数学模拟试卷
卷II(非选择题,共100分)
注意事项:1.答卷II前,将密封线左侧的项目填写清楚.
2.答卷II时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.
二、填空题(本大题共6个小题;每小题3分,共18分.把答案写在题中横线上)
13.单项式的系数是 .(原创)
14. 化简的结果是 .(原创)
15.如图,在中,分别是的中点,若,则 cm.(原创)
16.已知x、y满足方程组则x-y的值为 .(原创)
17.如图,AO为入射光线,OB为反射光线.已知A(-2, 3),由光的反射原理:入射角等于反射角,得到OB所在直线的解析式为 .(摘自2008河北省模拟试卷)
18.如图,在中,,于,若,,则= .(原创)
三、解答题(本大题共8个小题;共78分.解答应写出文字说明、证明过程或演算步骤)
19.(本小题满分8分)(原创)
已知,求的值.
20.(本小题满分8分)(根据2007江西省中考试题改编)
某校为研究学生的课余爱好情况,采取抽样的方法,从阅读、运动、娱乐、其它等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制了如下的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了 名学生,计算四个方面爱好人数的极差;
(2)补全频数分布折线图;
(3)若该校共1500名学生,估计全校爱好运动的学生有多少 名;
(4)在全校同学中随机选出一名学生参加演讲比赛,选出的恰好是爱好阅读的学生的概率是 .
21.(本小题满分10分)((根据2008河北省中考试卷改编)
已知:如图△ABC内接于⊙O,于H,过A点的切线与OC的延长线交于点D,°,.请求出:
(1)线段AC的长;
(2)劣弧AC的长(结果保留);
(3)线段AD的长.
22.(本小题满分10分)((根据2008河北省中考试卷改编))
阅读理解
对于任意正实数,,,
,只有当时,等号成立.
结论:在(均为正实数)中,若为定值,则,只有当时,有最小值.
根据上述内容,回答下列问题:
若,只有当 时,有最小值 .
思考验证
如图,为半圆的直径,为半圆上任意一点,(与点不重合).过点作,垂足为,,.
试根据图形验证,并指出等号成立时的条件.
探索应用
已知x>0,求代数式的最小值,并说明等号成立的条件.
23.(本小题满分10分)(模仿2007河北省中考试卷)
如图,已知抛物线经过点A、B、C,顶点为点D,与x轴的另一交点为E.
(1)求抛物线的解析式及顶点坐标;
(2)求四边形ABDE的面积;
(3)求抛物线顶点D关于x轴对称的点D'的坐标,并判断四边形ADE D'是何特殊四边形.(不要求说明理由)
24.(本小题满分12分)(根据2007河北省中考改编)
如图24-1,在△ABC中,∠BAC=90°,点D为射线BC上一点,连接AD,以AD为边且在AD的右侧作正方形ADEF.解答下列问题:
(1)如果AB=AC,
①当点D在线段BC上时(与点B不重合),如图24-2,请你通过观察、测量,猜想并写出CF与BD所满足的数量关系和位置关系;
②当点D在线段BC的延长线上时,如图24-3,猜想并写出CF与BD所满足的数量关系和位置关系,请证明你的猜想;
(2)不论点D在射线BC上运动到何处总有CF⊥BC(点C,F重合除外),求证:AB=AC
25.本小题满分12分(根据2007河北省中考改编)
某工程机械厂根据市场需求,计划生产A、B两种型号的大型挖掘机共100台,该厂所筹生产资金不少于22400万元,但不超过22500万元,且所筹资金全部用于生产此两型挖掘机,所生产的此两型挖掘机可全部售出,此两型挖掘机的生产成本和售价如下表:
型号 A B
成本(万元/台) 200 240
售价(万元/台) 250 300
设生产A型挖掘机x台
(1)求该厂对这两型挖掘机有哪几种生产方案?
(2))设该厂出售挖掘机获得利润W万元,求该厂如何生产能获得最大利润?
(3)根据市场调查,每台B型挖掘机的售价不会改变,每台A型挖掘机的售价将会提高m万元(m>0),该厂应该如何生产可以获得最大利润?(注:利润=售价-成本)
26.(本小题满分12分)(摘自2008河北省中考模拟试卷)
如图,Rt△ABC中,∠B=90°,∠CAB=30°.它的顶点A的坐标为(10,0),顶点B的坐标为(5,),AB=10,点P从点A出发,沿折线A→B→C以2个单位/秒的速度运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
(1)求∠BAO的度数及运动2秒时△OPQ的面积;
(2)当点P在AB上运动,求t为何值时,?
(3)当点P在AB上运动时,求△OPQ的面积S(平方单位)与时间t(秒)之间的函数关系式(不要求写出函数的自变量取值范围)及面积S取最大值时点P的坐标;
(4)点P沿AB边运动时,∠OPQ的大小随着时间t的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间t的增大而减小.当点P沿这两边运动时,使∠OPQ=90°的点P有几个?请通过画图、测量等方法得出结果,并说明理由.
九年级数学模拟试卷答案
一、选择题(每小题2分,共24分)
题 号 1 2 3 4 5 6 7 8 9 10
答 案 C C B D A C B A A B
二、填空题(每小题3分,共18分)
13. 14.3 15.4 16.1 17. 18.
三、解答题(本大题共8个小题;共78分)
19.解:原式=……………………………………………………4分
=…………………………………………………………………5分
当x=时,原式=4.……………………………………………………8分
(注:本题若直接代入求值,结果正确也相应给分)
20.解:(1)100……………………………………………………………………1分
因为爱好阅读学生为100×30%=30名,爱好其它学生为10名,由图可知爱好运动和娱乐学生分别为40和20名,所以四个方面爱好人数的极差为40-10=30名;………………………………………………………………………………………3分
()图略……………………………………………………………………………5分
(3)600……………………………………………………………………………6分
(4)……………………………………………………………………………8分
21.解:(1)连结OA,
……………………………………………………………1分
,OH =5 ∴AC=2AH=2·OH·= ……………………4分
(2)OA=OC=AC
∴劣弧AC的长=
∴劣弧AC的长是…………………………………………………………7分
(3) ∵AD是切线 ∴ ……………………………………………8分
∵ ∴AD=·OA=10
∴线段AD的长是10…………………………………………………………………10分
22.阅读理解:1(写不扣分),2…………………………………………4分
思考验证:AB是直径,……………………………………………5分
又
~ …………………………………………………………6分
CD=
若点D与O不重合,连接OC,在中,OC>CD>
若点D与O重合,OC=CD=
综上所述,≥即,当CD等于半径时,等号成立……7分
探索应用:=
x>0≥即≥6
有最小值6,此时有最小值12
只有当时,即时,等号成立……………………………………………10分
23.(1)设抛物线的解析式为……………………………1分
抛物线经过点A、B、C
抛物线的解析式为,…………………………………………3分
顶点D(1,4)………………………………………………………………………5分
(2)E(3,0)………………………………………………………………………6分
==9…………8分
(3)D'(1,-4)
四边形ADE D'是菱形………………………………………………………………10分
24.(1)①CF=BD,CF⊥BD………………………………………………………2分
②CF=BD,CF⊥BD…………………………………………………………………4分
证明:∵ABCD为正方形∴∠DAF=∠BAC=90°∴∠BAD=∠CAF
∵AD=AF,AB=AC∴△ABD≌△ACF,……………………………………………7分
∴CF=BD,∠ACF=∠B=45°
∴∠BCF=90°即CF⊥BD…………………………………………………………8分
(2)将(1)的证明过程逆过来 …………………………………………………12分
25.解 :(1)设生产A型挖掘机x台,则B型挖掘机可生产(100-x)台,………1分
由题意知 ,…………………………………3分
解得37.5≤x≤40…………………………………………………………………4分
∵x取非负整数,∴x为38,39,40∴有三种生产方案:A型38台,B型62台;A型39台,B型61台;A型40台,B型60台.………………………………………………………5分
(2)设获得利润W万元,由题意知W=50x+60(100-x)=6000-10 x………………7分
∴当x=38时,W最大=5620万元,即生产A型38台,B型62台获得利润最大.………9分
(3)由题意知W=(50+m)x+60(100-x)=6000+( m -10) x……………………10分
∴当0
当m>10时,则x=40时,W最大,即生产A型40台,B型60台.……………12分
26.解:(1)∠BAO =60°;运动2秒时,OQ=2+4=6,AP=4,点P的横坐标是10-=8,
所以此时△OPQ的面积=;……………………………………… 4分
(2)2.5秒
(3)点P在AB上运动时,OQ=2+2t,AP=2t,点P的横坐标是10-=10-t,
∴=.……………………………………………6分
∴当时,面积S最大.…………………………………………7分
这时点P的横坐标是10-t=;
点P的纵坐标是=.
即P(,); …………………………………………………………9分
(4)当点沿这两边运动时,使∠OPQ=90°的点P有2个.…………………11分
当点P与点A重合时,∠OPQ<90°,当点P运动到与点B重合时,画图(或测量) 知,∠OPQ>90°.所以当点P在AB边上运动时,使∠OPQ=90°的点P有1个.同理当点P运动到与点C重合时, ∠OPQ<90°,所以当点P在BC边上运动时,使∠OPQ=90°的点P也有1个.当点沿这两边运动时,使∠OPQ=90°的点P有2个.………………………………………………………………………………12分
1
0
A
x
1
0
B
x
1
0
C
x
1
0
D
x
P
M
M
M
M
Q
l
l
l
l
P
Q
P
Q
P
Q
P
Q
A
B
C
D
(第12题)
l
B
y
A
(第17题)
O
A
C
B
D
(第18题)
C
A
E
D
B
(第15题)
x
运动
娱乐
阅读
其它
项目
10
20
30
40
50
人数
O
图20-1
其它
运动
30%
娱乐
20%
阅读
图20-2
O
A
D
B
C
H
A
O
D
B
C
x
y
O
3
-
-2
A
B
D
E
C(2,3)
B
F
E
D
C
A
图24-2
B
F
E
D
C
A
图24-1
B
F
D
C
A
图24-3
E
O
A
C
B
P
Q
D
x
y
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
