2024-2025学年山东省济南市高新区五年级(上)期末数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年山东省济南市高新区五年级(上)期末数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 240.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-24 19:22:04 | ||
图片预览




文档简介
2024-2025学年山东省济南市高新区五年级(上)期末数学试卷
一、填一填。(每空1分,共21分)
1.(2分)3.46×0.54的积是 位小数,积保留一位小数是 。
2.(3分)6÷11的商用循环小数表示是 ,精确到百分位是 ,小数点后第2025位上的数字是 。
3.(1分)已知205.8÷□(□是一位数)的商接近30,但比30小,那么□里应该填 。
4.(2分)过十字路口要看红绿灯,红绿灯中也藏着数学问题。某十字路口红绿灯的时间设置为:红灯90秒,黄灯3秒,绿灯25秒。当你随意经过路口时,遇到的交通信号灯有
种可能,遇到 灯可能性最大。
5.(2分)毛泽东的诗词总是给人以力量和希望。在《卜算子 咏梅》中有一句“已是悬崖百丈冰,犹有花枝俏”。“一丈”等于我们现在的3.33……米,用简便方法可以记为 米,那么“百丈”约等于 米。【保留整数】
6.(1分)一个油桶能装油5.5千克,装70千克油至少需要这样的油桶 个.
7.(2分)小通在学习中发现,如图的这个梯形可以分割成等底等高的一个平行四边形和一个三角形。已知图中的三角形面积是15cm2,平行四边形的高是6cm。那么,梯形的下底长 cm,梯形的面积是 cm2。
8.(2分)根据1.56×2.4=3.744,不计算填出结果。
1.56×0.24= 0.156×24=
9.(1分)为积极响应国家节能环保政策,研发了一款纯电动汽车,该款电动汽车行驶100km耗电量为12千瓦时,平均1千瓦时电可以行驶 km。(得数保留两位小数)。
10.(1分)用黑、白两种颜色的圆摆图形。像这样继续摆下去,摆第7幅图需要 个。
11.(1分)街道上有大小两种混凝土圆球(如图),这些圆球是为了防止车辆停泊而设置的.每一个球都被牢固的固定在地面的某一点.相邻两个球的固定间距是1.7米,在相邻两个大球之间放置13个小球.相邻两个大球固定点之间的距离是 米.
12.(3分)请根据下面的信息,在圆盘中的方框里填写适当的数。
a.圆盘上标有三个连续的自然数。
b.指针旋转后,不可能停留在比6大的数。
c.指针旋转后,可能停留在5。
d.指针旋转后,可能停留在与5相差2的数。
二、选择正确答案的序号填在括号里。(每题1分,共12分)
13.(1分)a和b都是大于零的数,a×0.9=b,那么( )
A.a>b B.a=b C.a<b D.无法确定
14.(1分)如果□×〇=4.8,则(□×2)×(〇÷2)=( )
A.2.4 B.4.8 C.9.6 D.19.2
15.(1分)“神舟十三号”航天员乘组在空间站组合体工作生活了183天,刷新了中国航天员单次飞行任务太空驻留时间的记录,比“神舟十二号”航天员乘组在空间站组合体工作生活时长的2倍还多3天。如果用“x”表示“神舟十二号”航天员乘组在空间站组合体工作生活的天数,那么解决“神舟十二号”航天员乘组在空间站组合体工作生活的天数”这个问题,下面所列方程中不正确的是( )
A.2x+3=183 B.183﹣2x=3 C.2x=183+3 D.2x=183﹣3
16.(1分)A÷B=12……5,则10A÷10B的余数是( )
A.5 B.50 C.100 D.500
17.(1分)一个三角形的底扩大到原来的2倍,高不变,它的面积( )
A.扩大到原来的2倍 B.不变
C.扩大到原来的4倍 D.无法确定
18.(1分)明天胜利小学将举办爱心义卖活动,同学们都很期待吧?
“明天降水的可能性为20%”,表示明天( )
A.一定下雨 B.下雨的可能性较小
C.不可能下雨 D.下雨的可能性很大
19.(1分)甲数是a,比乙数少15,表示两数和的式子是( )
A.2a+15 B.2a﹣15 C.a+15 D.a﹣15
20.(1分)甲乙两筐苹果,甲筐32千克,乙筐x千克.从甲筐拿4千克放入乙筐,两筐苹果就一样重.下列方程正确的是( )
A.32﹣x=4 B.x+4=32 C.x﹣8=32 D.x+4=32﹣4
21.(1分)如图是一道小数乘法的竖式,在竖式计算过程中,把第一次乘得的积记作“甲”,把第二次乘得的积记作“乙”。能反映甲、乙关系的是( )
A. B. C. D.
22.(1分)上午7时我军监控到一架它国不明无人侦察机在东经161°,北纬37°,我侦察员用数对表示其位置是(161,37),到了上午8时,该架无人侦察机的位置是(178,16),此时它的位置处于( )
A.东经16°,北纬178° B.东纬178°,北经16°
C.东经178°,北纬16° D.东纬16°,北经178°
23.(1分)在如图所示的梯形中,甲的面积( )乙的面积。
A.大于 B.等于 C.小于 D.无法确定
24.(1分)我国古代数学家刘徽利用出入相补原理来计算平面图形的面积。出入相补原理就是把一个图形分割、移补,而面积保持不变。把下图中的三角形先沿虚线剪开,再将两部分重新拼成一个新图形(两部分不重叠),不可能拼成的图形是( )
A.长方形 B.平行四边形
C.等腰梯形 D.直角梯形
三、计算题(共33分)
25.(4分)直接写得数。
0.3×0.8= 3.6÷0.3= 0.8÷4= 6x+x=
7.2÷6= 0.2×0.45= 1.25×0.8×0= 0.2×1.5÷1.5=
26.(8分)列竖式计算。
12.7×5.8= 51.3÷0.27=
27.5×0.046≈(得数保留两位小数) 8.27÷1.1=(商用循环小数表示)
27.(9分)脱式计算,能简便的用简便方法计算。
7.2÷(0.8+1.2) 5.1×7.3+2.7×5.1 12.5×8.8×0.3
28.(9分)解方程。
2x﹣7.5=8.5 12(x+5)=156 5.2x﹣2.5x=8.91
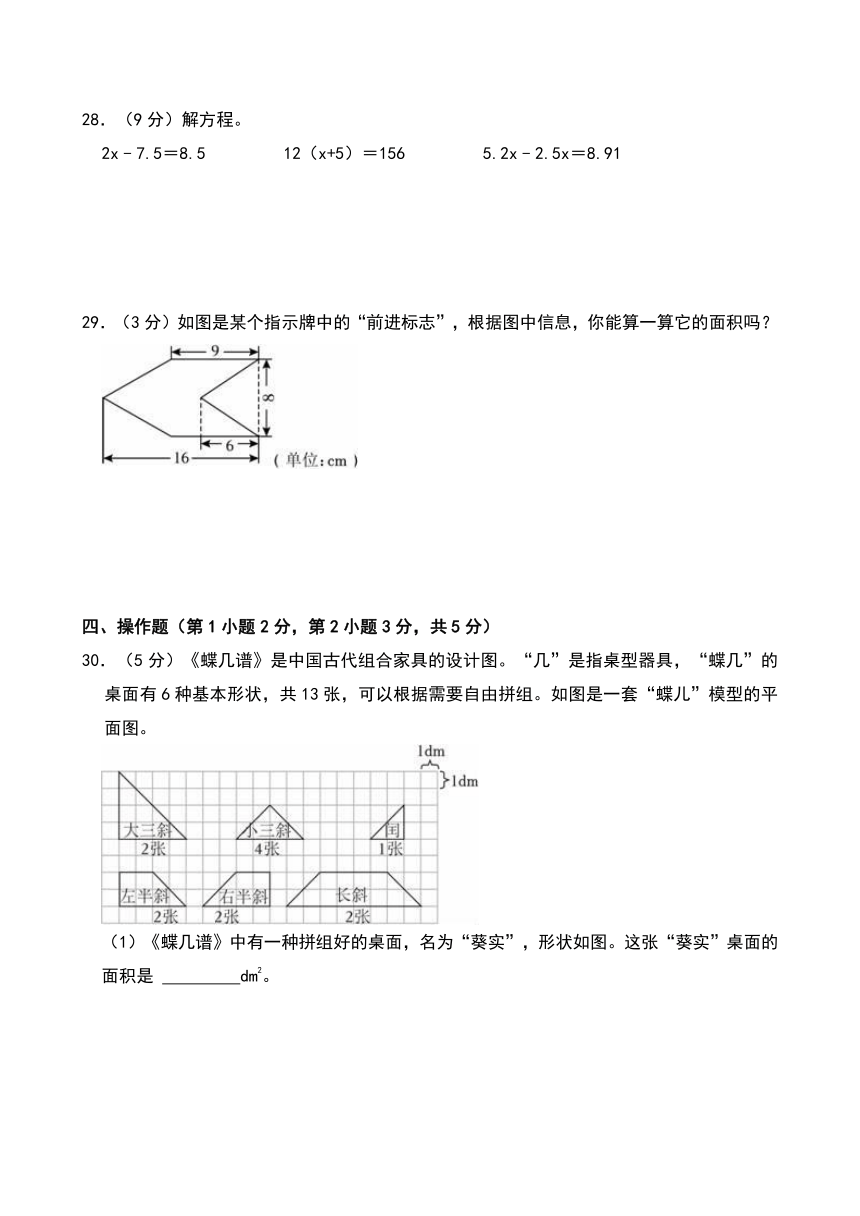
29.(3分)如图是某个指示牌中的“前进标志”,根据图中信息,你能算一算它的面积吗?
四、操作题(第1小题2分,第2小题3分,共5分)
30.(5分)《蝶几谱》是中国古代组合家具的设计图。“几”是指桌型器具,“蝶几”的桌面有6种基本形状,共13张,可以根据需要自由拼组。如图是一套“蝶儿”模型的平面图。
(1)《蝶几谱》中有一种拼组好的桌面,名为“葵实”,形状如图。这张“葵实”桌面的面积是 dm2。
(2)“葵实”可以由哪几种基本形状的桌面拼组成,把你的拼组方案画在图中。(注意每种基本形状桌面的张数。)
五.解决问题(1-6小题每题4分,第7小题5分,共29分)
31.(4分)一个普通番茄约重0.36千克,“太空种子”结出的番茄重约是它的2.8倍.“太空种子”结出的番茄约重多少千克?
32.(4分)孙老师要用80元买一些文具作为年级运动会的奖品。他先用45.6元买了8本相册,剩下的钱准备用来买2.5元一支的笔,可以买多少支?
33.(4分)小明和丽丽在超市购物,结完账的时间是16:42,从他们所在的位置步行到停车场需要10分钟。(停车计费单上显示13:00进入超市停车场)
路边临时停车收费标准
时段 收费标准
半小时内 免费
2小时以内 10元/车 次
超过2小时的部分(不足半小时按半小时计算) 6.5元/车 半小时
(1)如果他们现在去停车场,离开时需要支付多少停车费?
(2)你支持公共停车场设置阶段递增收费标准吗?请说明理由。
34.(4分)位于大明湖畔的超然楼,被誉为“江北第一楼”。每天都会有大量游客在此游玩,据调查,“十一”当天有3361名游客登上超然楼,比工作日平均一天的3倍还多25名,工作日平均一天的游客有多少名?(列方程解答)
35.(4分)甲、乙两队学生从相距17km的两地出发,相向而行。如果甲队学生每小时走4.5km,乙队学生每小时走4km,两队学生多长时间后相遇?
(1)用自己喜欢的方式画一个示意图,表示数量关系。
(2)列式解答。
36.(4分)大约在两千年前,我国数学名著《九章算术》中的“方田章”就论述了平面图形面积的算法。书中说:“圭田术曰,半广以乘正从。”其中“圭田”就是指三角形田地,“广”和“从”是指三角形的底和高,已知三角形的面积是35.2平方米,底是4.4米,它的高是多少米?
37.(5分)小明叔叔是一名热爱自然与科学的探险者。他在一次登山时,看到这样的风景:“山顶白雪皑皑,山脚春暖花开”。为此他查阅了相关资料得知:
(1)如果用t表示海平面温度,h表示山的海拔高度,请你帮小明叔叔设计一个计算山顶温度的式子(用字母表示) ℃。
(2)小明叔叔决定去攀登泰山(高度大约1500m)验证一下!如果海平面温度是20°C,那么小明叔叔登到山山顶时的温度大约是多少摄氏度?
(3)他计划攀登一座未知高度的山峰,并希望通过测量海平面温度和山顶温度来估算山峰的高度。假设你是小明叔叔,写一写你的方案和计算过程。(温度可自行设计)
参考答案
一、填一填。(每空1分,共21分)
1.解:3.46×0.54=1.8684
3.12是四位小数,保留一位小数越是1.9。
故答案为:四,1.9。
2.解:6÷11=0.5454……≈0.55
2025÷2=1012......1
所以,小数点后第2025位上的数字是5。
故答案为:0.5454……,0.55,5。
3.解:205.8÷30≈7
答:□里应该填7。
故答案为:7。
4.解:90>25>3
当你随意经过路口时,遇到的交通信号灯有3种可能,遇到红灯可能性最大。
故答案为:3;红。
5.解:3.333……=3.
100丈=333.333……米≈333米
答:“一丈”等于我们现在的3.33……米,用简便方法可以记为3.米,那么“百丈”约等于333米。
故答案为:3.;333。
6.解:70÷5.5≈13(个);
答:装70千克油至少需要这样的油桶13个.
故答案为:13.
7.解:第一问:
上底:15×2÷6
=30÷6
=5(cm)
下底:5×2=10(cm)
面积:15×2+15=45(cm2)
答:梯形的下底长10cm,梯形的面积是45cm2。
故答案为:10;45。
8.解:1.56×2.4=3.744
所以1.56×0.24=0.3744
0.156×24=3.744
故答案为:0.3744;3.744。
9.解:100÷12≈8.33(km)
答:平均1千瓦时电可以行驶8.33km。
故答案为:8.33。
10.解:第7幅图有:
2×(7+1)
=2×8
=16(个)
答:摆第7幅图需要16个。
故答案为:16。
11.解:1.7×(13+1)
=1.7×14
=23.8(米)
答:相邻两个大球固定点之间的距离是23.8米.
故答案为:23.8.
12.解:如图所示:
。
二、选择正确答案的序号填在括号里。(每题1分,共12分)
13.解:设a=1
a×0.9=1×0.9=0.9
即b=0.9
1>0.9
a>b
故选:A。
14.解:如果□×〇=4.8,则(□×2)×(〇÷2)=4.8。
故选:B。
15.解:如果用“x”表示“神舟十二号”航天员乘组在空间站组合体工作生活的天数,那么解决“神舟十二号”航天员乘组在空间站组合体工作生活的天数”这个问题,可以列方程为:2x+3=183、183﹣2x=3或2x=183﹣3,方程2x=183+3是错误的。
故选:C。
16.解:因为5×10=50,所以,A÷B=12……5,则10A÷10B的余数是50。
故选:B。
17.解:由分析得:一个三角形的底扩大到原来的2倍,高不变,它的面积扩大到原来的2倍。
故选:A。
18.解:“明天降水的可能性为20%”,表示明天下雨的可能性较小。
故选:B。
19.解:a+15+a=2a+15
故选:A。
20.解:设乙筐x千克,
32﹣4=x+4,
故选:D.
21.解:分析可知,甲表示0.5与第一个因数的积,乙表示2与第一个因数的积。
2÷0.5=4
所以,乙是甲的4倍,能反映甲、乙关系的是。
故选:D。
22.解:根据题干分析可得,该架无人侦察机的位置是(178,16),此时它的位置处于东经178°、北纬16°。
故选:C。
23.解:由图可知,两个阴影三角形分别加上顶部的空白三角形后组成两个新的三角形,由于这两个新三角形是等底等高的,面积相等,所以两个阴影三角形的面积是相等的。
答:甲的面积等于乙的面积。
故选:B。
24.解:如图:
把上面的部分绕左下的点逆时针旋转90°与原来的图形拼成平行四边形;
把上面的部分绕右下的点顺时针旋转90°与原来的图形拼成长方形;
把上面的部分翻面后,与下面的图形拼成等腰梯形。
答:不能拼成直角梯形。
故选:D。
三、计算题(共33分)
25.解:0.3×0.8=0.24 3.6÷0.3=12 0.8÷4=0.2 6x+x=7x
7.2÷6=1.2 0.2×0.45=0.09 1.25×0.8×0=0 0.2×1.5÷1.5=0.2
26.解:12.7×5.8=73.66
51.3÷0.27=190
27.5×0.046≈1.27
8.27÷1.1=7.5
27.解:7.2÷(0.8+1.2)
=7.2÷2
=3.6
5.1×7.3+2.7×5.1
=5.1×(7.3+2.7)
=5.1×10
=51
12.5×8.8×0.3
=(12.5×8)×(1.1×0.3)
=100×0.33
=33
28.解:2x﹣7.5=8.5
2x﹣7.5+7.5=8.5+7.5
2x=16
x=8
12(x+5)=156
12(x+5)÷12=156÷12
x+5=13
x=8
5.2x﹣2.5x=8.91
2.7x=8.91
x=3.3
29.解:8×(16﹣9)÷2+9×8﹣8×6÷2
=56÷2+72﹣24
=76(平方厘米)
答:指示牌中的“前进标志”的面积是76平方厘米。
四、操作题(第1小题2分,第2小题3分,共5分)
30.解:(1)(2+6)×2÷2×2
=8×2÷2×2
=16÷2×2
=16(平方分米)
答:这张“葵实”桌面的面积是16平方分米。
(2)这个葵实”可以由“左半斜”一张,“右半斜”一张,“闰”2张拼组成的。
作图如下:
故答案为:16。
五.解决问题(1-6小题每题4分,第7小题5分,共29分)
31.解:0.36×2.8=1.008(千克)
答:“太空种子”结出的番茄约重1.008千克.
32.解:(80﹣45.6)÷2.5
=34.4÷2.5
≈13(支)
答:可以买13支。
33.解:(1)16时42分+10分=16时52分
16时52分﹣13时=3时52分
3时52分﹣2时=1时52分
1时52分按2小时计算,
10+6.5×2
=10+13
=23(元)
答:离开时需要支付23元停车费。
(2)支持公共停车场设置阶段递增收费标准,因为这样可以鼓励大家短时停车,减少长时间停车,缓解停车压力。
34.解:设工作日平均一天的游客有x名。
3x+25=3361
3x=3336
x=1112
答:工作日平均一天的游客有1112名。
35.解:(1)如下图所示:
数量关系:甲队行驶的路程+乙队行驶的路程=17km
(2)设两队学生x小时间后相遇,则:
(4.5+4)x=17
8.5x=17
8.5x÷8.5=17÷8.5
x=2
答:两队学生2小时后相遇。
36.解:35.2×2÷4.4
=70.8÷4.4
=16(米)
答:它的高是16米。
37.解:(1)根据分析可知,计算山顶温度的式子是:t﹣×0.6;
(2)t﹣×0.6
=20﹣×0.6
=20﹣9
=11(°C)
答:小明叔叔登到泰山山顶时的温度大约是11摄氏度。
(3)根据题分析可知,用t表示海平面温度,用v表示山顶温度,那么计算山峰高度的式子就是:(t﹣v)÷0.6×100。
假设海平面温度是22℃,山顶温度是10°C,那么
(t﹣v)÷0.6×100
=(22﹣10)÷0.6×100
=12÷0.6×100
=20×100
=2000(m)
答:山峰的高度是2000米。
故答案为:(1)t﹣×0.6。
一、填一填。(每空1分,共21分)
1.(2分)3.46×0.54的积是 位小数,积保留一位小数是 。
2.(3分)6÷11的商用循环小数表示是 ,精确到百分位是 ,小数点后第2025位上的数字是 。
3.(1分)已知205.8÷□(□是一位数)的商接近30,但比30小,那么□里应该填 。
4.(2分)过十字路口要看红绿灯,红绿灯中也藏着数学问题。某十字路口红绿灯的时间设置为:红灯90秒,黄灯3秒,绿灯25秒。当你随意经过路口时,遇到的交通信号灯有
种可能,遇到 灯可能性最大。
5.(2分)毛泽东的诗词总是给人以力量和希望。在《卜算子 咏梅》中有一句“已是悬崖百丈冰,犹有花枝俏”。“一丈”等于我们现在的3.33……米,用简便方法可以记为 米,那么“百丈”约等于 米。【保留整数】
6.(1分)一个油桶能装油5.5千克,装70千克油至少需要这样的油桶 个.
7.(2分)小通在学习中发现,如图的这个梯形可以分割成等底等高的一个平行四边形和一个三角形。已知图中的三角形面积是15cm2,平行四边形的高是6cm。那么,梯形的下底长 cm,梯形的面积是 cm2。
8.(2分)根据1.56×2.4=3.744,不计算填出结果。
1.56×0.24= 0.156×24=
9.(1分)为积极响应国家节能环保政策,研发了一款纯电动汽车,该款电动汽车行驶100km耗电量为12千瓦时,平均1千瓦时电可以行驶 km。(得数保留两位小数)。
10.(1分)用黑、白两种颜色的圆摆图形。像这样继续摆下去,摆第7幅图需要 个。
11.(1分)街道上有大小两种混凝土圆球(如图),这些圆球是为了防止车辆停泊而设置的.每一个球都被牢固的固定在地面的某一点.相邻两个球的固定间距是1.7米,在相邻两个大球之间放置13个小球.相邻两个大球固定点之间的距离是 米.
12.(3分)请根据下面的信息,在圆盘中的方框里填写适当的数。
a.圆盘上标有三个连续的自然数。
b.指针旋转后,不可能停留在比6大的数。
c.指针旋转后,可能停留在5。
d.指针旋转后,可能停留在与5相差2的数。
二、选择正确答案的序号填在括号里。(每题1分,共12分)
13.(1分)a和b都是大于零的数,a×0.9=b,那么( )
A.a>b B.a=b C.a<b D.无法确定
14.(1分)如果□×〇=4.8,则(□×2)×(〇÷2)=( )
A.2.4 B.4.8 C.9.6 D.19.2
15.(1分)“神舟十三号”航天员乘组在空间站组合体工作生活了183天,刷新了中国航天员单次飞行任务太空驻留时间的记录,比“神舟十二号”航天员乘组在空间站组合体工作生活时长的2倍还多3天。如果用“x”表示“神舟十二号”航天员乘组在空间站组合体工作生活的天数,那么解决“神舟十二号”航天员乘组在空间站组合体工作生活的天数”这个问题,下面所列方程中不正确的是( )
A.2x+3=183 B.183﹣2x=3 C.2x=183+3 D.2x=183﹣3
16.(1分)A÷B=12……5,则10A÷10B的余数是( )
A.5 B.50 C.100 D.500
17.(1分)一个三角形的底扩大到原来的2倍,高不变,它的面积( )
A.扩大到原来的2倍 B.不变
C.扩大到原来的4倍 D.无法确定
18.(1分)明天胜利小学将举办爱心义卖活动,同学们都很期待吧?
“明天降水的可能性为20%”,表示明天( )
A.一定下雨 B.下雨的可能性较小
C.不可能下雨 D.下雨的可能性很大
19.(1分)甲数是a,比乙数少15,表示两数和的式子是( )
A.2a+15 B.2a﹣15 C.a+15 D.a﹣15
20.(1分)甲乙两筐苹果,甲筐32千克,乙筐x千克.从甲筐拿4千克放入乙筐,两筐苹果就一样重.下列方程正确的是( )
A.32﹣x=4 B.x+4=32 C.x﹣8=32 D.x+4=32﹣4
21.(1分)如图是一道小数乘法的竖式,在竖式计算过程中,把第一次乘得的积记作“甲”,把第二次乘得的积记作“乙”。能反映甲、乙关系的是( )
A. B. C. D.
22.(1分)上午7时我军监控到一架它国不明无人侦察机在东经161°,北纬37°,我侦察员用数对表示其位置是(161,37),到了上午8时,该架无人侦察机的位置是(178,16),此时它的位置处于( )
A.东经16°,北纬178° B.东纬178°,北经16°
C.东经178°,北纬16° D.东纬16°,北经178°
23.(1分)在如图所示的梯形中,甲的面积( )乙的面积。
A.大于 B.等于 C.小于 D.无法确定
24.(1分)我国古代数学家刘徽利用出入相补原理来计算平面图形的面积。出入相补原理就是把一个图形分割、移补,而面积保持不变。把下图中的三角形先沿虚线剪开,再将两部分重新拼成一个新图形(两部分不重叠),不可能拼成的图形是( )
A.长方形 B.平行四边形
C.等腰梯形 D.直角梯形
三、计算题(共33分)
25.(4分)直接写得数。
0.3×0.8= 3.6÷0.3= 0.8÷4= 6x+x=
7.2÷6= 0.2×0.45= 1.25×0.8×0= 0.2×1.5÷1.5=
26.(8分)列竖式计算。
12.7×5.8= 51.3÷0.27=
27.5×0.046≈(得数保留两位小数) 8.27÷1.1=(商用循环小数表示)
27.(9分)脱式计算,能简便的用简便方法计算。
7.2÷(0.8+1.2) 5.1×7.3+2.7×5.1 12.5×8.8×0.3
28.(9分)解方程。
2x﹣7.5=8.5 12(x+5)=156 5.2x﹣2.5x=8.91
29.(3分)如图是某个指示牌中的“前进标志”,根据图中信息,你能算一算它的面积吗?
四、操作题(第1小题2分,第2小题3分,共5分)
30.(5分)《蝶几谱》是中国古代组合家具的设计图。“几”是指桌型器具,“蝶几”的桌面有6种基本形状,共13张,可以根据需要自由拼组。如图是一套“蝶儿”模型的平面图。
(1)《蝶几谱》中有一种拼组好的桌面,名为“葵实”,形状如图。这张“葵实”桌面的面积是 dm2。
(2)“葵实”可以由哪几种基本形状的桌面拼组成,把你的拼组方案画在图中。(注意每种基本形状桌面的张数。)
五.解决问题(1-6小题每题4分,第7小题5分,共29分)
31.(4分)一个普通番茄约重0.36千克,“太空种子”结出的番茄重约是它的2.8倍.“太空种子”结出的番茄约重多少千克?
32.(4分)孙老师要用80元买一些文具作为年级运动会的奖品。他先用45.6元买了8本相册,剩下的钱准备用来买2.5元一支的笔,可以买多少支?
33.(4分)小明和丽丽在超市购物,结完账的时间是16:42,从他们所在的位置步行到停车场需要10分钟。(停车计费单上显示13:00进入超市停车场)
路边临时停车收费标准
时段 收费标准
半小时内 免费
2小时以内 10元/车 次
超过2小时的部分(不足半小时按半小时计算) 6.5元/车 半小时
(1)如果他们现在去停车场,离开时需要支付多少停车费?
(2)你支持公共停车场设置阶段递增收费标准吗?请说明理由。
34.(4分)位于大明湖畔的超然楼,被誉为“江北第一楼”。每天都会有大量游客在此游玩,据调查,“十一”当天有3361名游客登上超然楼,比工作日平均一天的3倍还多25名,工作日平均一天的游客有多少名?(列方程解答)
35.(4分)甲、乙两队学生从相距17km的两地出发,相向而行。如果甲队学生每小时走4.5km,乙队学生每小时走4km,两队学生多长时间后相遇?
(1)用自己喜欢的方式画一个示意图,表示数量关系。
(2)列式解答。
36.(4分)大约在两千年前,我国数学名著《九章算术》中的“方田章”就论述了平面图形面积的算法。书中说:“圭田术曰,半广以乘正从。”其中“圭田”就是指三角形田地,“广”和“从”是指三角形的底和高,已知三角形的面积是35.2平方米,底是4.4米,它的高是多少米?
37.(5分)小明叔叔是一名热爱自然与科学的探险者。他在一次登山时,看到这样的风景:“山顶白雪皑皑,山脚春暖花开”。为此他查阅了相关资料得知:
(1)如果用t表示海平面温度,h表示山的海拔高度,请你帮小明叔叔设计一个计算山顶温度的式子(用字母表示) ℃。
(2)小明叔叔决定去攀登泰山(高度大约1500m)验证一下!如果海平面温度是20°C,那么小明叔叔登到山山顶时的温度大约是多少摄氏度?
(3)他计划攀登一座未知高度的山峰,并希望通过测量海平面温度和山顶温度来估算山峰的高度。假设你是小明叔叔,写一写你的方案和计算过程。(温度可自行设计)
参考答案
一、填一填。(每空1分,共21分)
1.解:3.46×0.54=1.8684
3.12是四位小数,保留一位小数越是1.9。
故答案为:四,1.9。
2.解:6÷11=0.5454……≈0.55
2025÷2=1012......1
所以,小数点后第2025位上的数字是5。
故答案为:0.5454……,0.55,5。
3.解:205.8÷30≈7
答:□里应该填7。
故答案为:7。
4.解:90>25>3
当你随意经过路口时,遇到的交通信号灯有3种可能,遇到红灯可能性最大。
故答案为:3;红。
5.解:3.333……=3.
100丈=333.333……米≈333米
答:“一丈”等于我们现在的3.33……米,用简便方法可以记为3.米,那么“百丈”约等于333米。
故答案为:3.;333。
6.解:70÷5.5≈13(个);
答:装70千克油至少需要这样的油桶13个.
故答案为:13.
7.解:第一问:
上底:15×2÷6
=30÷6
=5(cm)
下底:5×2=10(cm)
面积:15×2+15=45(cm2)
答:梯形的下底长10cm,梯形的面积是45cm2。
故答案为:10;45。
8.解:1.56×2.4=3.744
所以1.56×0.24=0.3744
0.156×24=3.744
故答案为:0.3744;3.744。
9.解:100÷12≈8.33(km)
答:平均1千瓦时电可以行驶8.33km。
故答案为:8.33。
10.解:第7幅图有:
2×(7+1)
=2×8
=16(个)
答:摆第7幅图需要16个。
故答案为:16。
11.解:1.7×(13+1)
=1.7×14
=23.8(米)
答:相邻两个大球固定点之间的距离是23.8米.
故答案为:23.8.
12.解:如图所示:
。
二、选择正确答案的序号填在括号里。(每题1分,共12分)
13.解:设a=1
a×0.9=1×0.9=0.9
即b=0.9
1>0.9
a>b
故选:A。
14.解:如果□×〇=4.8,则(□×2)×(〇÷2)=4.8。
故选:B。
15.解:如果用“x”表示“神舟十二号”航天员乘组在空间站组合体工作生活的天数,那么解决“神舟十二号”航天员乘组在空间站组合体工作生活的天数”这个问题,可以列方程为:2x+3=183、183﹣2x=3或2x=183﹣3,方程2x=183+3是错误的。
故选:C。
16.解:因为5×10=50,所以,A÷B=12……5,则10A÷10B的余数是50。
故选:B。
17.解:由分析得:一个三角形的底扩大到原来的2倍,高不变,它的面积扩大到原来的2倍。
故选:A。
18.解:“明天降水的可能性为20%”,表示明天下雨的可能性较小。
故选:B。
19.解:a+15+a=2a+15
故选:A。
20.解:设乙筐x千克,
32﹣4=x+4,
故选:D.
21.解:分析可知,甲表示0.5与第一个因数的积,乙表示2与第一个因数的积。
2÷0.5=4
所以,乙是甲的4倍,能反映甲、乙关系的是。
故选:D。
22.解:根据题干分析可得,该架无人侦察机的位置是(178,16),此时它的位置处于东经178°、北纬16°。
故选:C。
23.解:由图可知,两个阴影三角形分别加上顶部的空白三角形后组成两个新的三角形,由于这两个新三角形是等底等高的,面积相等,所以两个阴影三角形的面积是相等的。
答:甲的面积等于乙的面积。
故选:B。
24.解:如图:
把上面的部分绕左下的点逆时针旋转90°与原来的图形拼成平行四边形;
把上面的部分绕右下的点顺时针旋转90°与原来的图形拼成长方形;
把上面的部分翻面后,与下面的图形拼成等腰梯形。
答:不能拼成直角梯形。
故选:D。
三、计算题(共33分)
25.解:0.3×0.8=0.24 3.6÷0.3=12 0.8÷4=0.2 6x+x=7x
7.2÷6=1.2 0.2×0.45=0.09 1.25×0.8×0=0 0.2×1.5÷1.5=0.2
26.解:12.7×5.8=73.66
51.3÷0.27=190
27.5×0.046≈1.27
8.27÷1.1=7.5
27.解:7.2÷(0.8+1.2)
=7.2÷2
=3.6
5.1×7.3+2.7×5.1
=5.1×(7.3+2.7)
=5.1×10
=51
12.5×8.8×0.3
=(12.5×8)×(1.1×0.3)
=100×0.33
=33
28.解:2x﹣7.5=8.5
2x﹣7.5+7.5=8.5+7.5
2x=16
x=8
12(x+5)=156
12(x+5)÷12=156÷12
x+5=13
x=8
5.2x﹣2.5x=8.91
2.7x=8.91
x=3.3
29.解:8×(16﹣9)÷2+9×8﹣8×6÷2
=56÷2+72﹣24
=76(平方厘米)
答:指示牌中的“前进标志”的面积是76平方厘米。
四、操作题(第1小题2分,第2小题3分,共5分)
30.解:(1)(2+6)×2÷2×2
=8×2÷2×2
=16÷2×2
=16(平方分米)
答:这张“葵实”桌面的面积是16平方分米。
(2)这个葵实”可以由“左半斜”一张,“右半斜”一张,“闰”2张拼组成的。
作图如下:
故答案为:16。
五.解决问题(1-6小题每题4分,第7小题5分,共29分)
31.解:0.36×2.8=1.008(千克)
答:“太空种子”结出的番茄约重1.008千克.
32.解:(80﹣45.6)÷2.5
=34.4÷2.5
≈13(支)
答:可以买13支。
33.解:(1)16时42分+10分=16时52分
16时52分﹣13时=3时52分
3时52分﹣2时=1时52分
1时52分按2小时计算,
10+6.5×2
=10+13
=23(元)
答:离开时需要支付23元停车费。
(2)支持公共停车场设置阶段递增收费标准,因为这样可以鼓励大家短时停车,减少长时间停车,缓解停车压力。
34.解:设工作日平均一天的游客有x名。
3x+25=3361
3x=3336
x=1112
答:工作日平均一天的游客有1112名。
35.解:(1)如下图所示:
数量关系:甲队行驶的路程+乙队行驶的路程=17km
(2)设两队学生x小时间后相遇,则:
(4.5+4)x=17
8.5x=17
8.5x÷8.5=17÷8.5
x=2
答:两队学生2小时后相遇。
36.解:35.2×2÷4.4
=70.8÷4.4
=16(米)
答:它的高是16米。
37.解:(1)根据分析可知,计算山顶温度的式子是:t﹣×0.6;
(2)t﹣×0.6
=20﹣×0.6
=20﹣9
=11(°C)
答:小明叔叔登到泰山山顶时的温度大约是11摄氏度。
(3)根据题分析可知,用t表示海平面温度,用v表示山顶温度,那么计算山峰高度的式子就是:(t﹣v)÷0.6×100。
假设海平面温度是22℃,山顶温度是10°C,那么
(t﹣v)÷0.6×100
=(22﹣10)÷0.6×100
=12÷0.6×100
=20×100
=2000(m)
答:山峰的高度是2000米。
故答案为:(1)t﹣×0.6。
同课章节目录
