北京市昌平一中2024-2025学年初三下开学考数学试卷(PDF版,无答案)
文档属性
| 名称 | 北京市昌平一中2024-2025学年初三下开学考数学试卷(PDF版,无答案) |
|
|
| 格式 | |||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-24 21:12:19 | ||
图片预览




文档简介
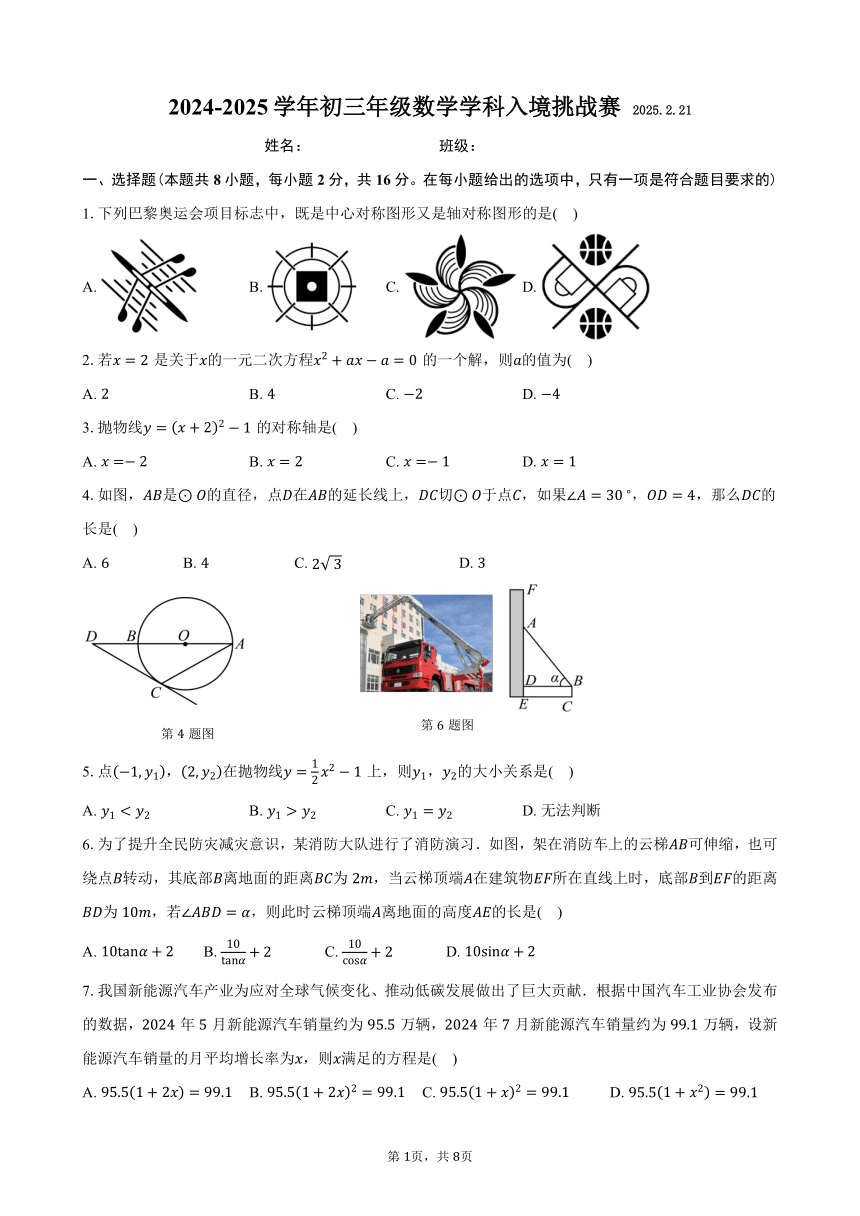
2024-2025 学年初三年级数学学科入境挑战赛 2025.2.21
姓名: 班级:
一、选择题(本题共 8 小题,每小题 2 分,共 16 分。在每小题给出的选项中,只有一项是符合题目要求的)
1.下列巴黎奥运会项目标志中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.若 = 2 是关于 的一元二次方程 2 + = 0 的一个解,则 的值为( )
A. 2 B. 4 C. 2 D. 4
3.抛物线 = + 2 2 1 的对称轴是( )
A. = 2 B. = 2 C. = 1 D. = 1
4.如图, 是⊙ 的直径,点 在 的延长线上, 切⊙ 于点 ,如果∠ = 30 , = 4,那么 的
长是( )
A. 6 B. 4 C. 2 3 D. 3
第 6 题图
第 4 题图
5.点 1, 1 , 2, 2 在抛物线 =
1 22 1 上,则 1, 2的大小关系是( )
A. 1 < 2 B. 1 > 2 C. 1 = 2 D.无法判断
6.为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图,架在消防车上的云梯 可伸缩,也可
绕点 转动,其底部 离地面的距离 为 2 ,当云梯顶端 在建筑物 所在直线上时,底部 到 的距离
为 10 ,若∠ = ,则此时云梯顶端 离地面的高度 的长是( )
A. 10tan + 2 B. 10tan + 2 C.
10
cos + 2 D. 10sin + 2
7.我国新能源汽车产业为应对全球气候变化、推动低碳发展做出了巨大贡献.根据中国汽车工业协会发布
的数据,2024 年 5 月新能源汽车销量约为 95.5 万辆,2024 年 7 月新能源汽车销量约为 99.1 万辆,设新
能源汽车销量的月平均增长率为 ,则 满足的方程是( )
A. 95.5 1 + 2 = 99.1 B. 95.5 1 + 2 2 = 99.1 C. 95.5 1 + 2 = 99.1 D. 95.5 1 + 2 = 99.1
第 1页,共 8页
8.如图,已知⊙ 及⊙ 外一定点 ,嘉嘉进行了如下操作后,得出了四个结论:
①点 是 的中点;②直线 , 都是⊙ 的切线;③点 到点 、点 的距离相等;
④连接 , , , 1, ,则 △ = 8 四边形 .对上述结论描述正确的是( )
A.只有①正确 B. 只有②正确 C.①②③正确 D.①②③④都正确
二、填空题(本题共 8 小题,每小题 2 分,共 16 分)
9.若 3在实数范围内有意义,则实数 的取值范围为 .
10.分解因式: 2 4 = ______.
11.已知二次函数满足条件:①有最大值;②它的图象经过点 1,0 ,写出一个满足上述所有条件的二次函
数的解析式 .
12.如图, 、 是 边 、 上的两点,且 // , : = 1: 3,那么 : = .
第 12 题图 第 13 题图 第 14 题图
13.图 1 为一个装有液体的圆底烧瓶(厚度忽略不计),侧面示意图如图 2,其液体水平宽度 为 16 ,竖
直高度 为 4 ,则⊙ 的半径为 .
14.如图, 是⊙ 的直径, , 是⊙ 的切线,切点分别为 , .若 = 2,∠ = 60 ,则 的
长是 .
15.小明看到公园地面上有一个心形封闭图形 ,为了研究图形 的面积,设计了一项试验:在图形 外部
绘制一个半径为 1 米的圆,如图所示,向这个圆内随机投掷石子.假设石子落在圆内的每一点都是等可能
的(不考虑边界),记录的试验数据如下:
掷石子的总次数 50100200500…
石子落在图形 内的次数 1543 80 201…
石子落在阴影部分的次数 3557 120299…
第 2页,共 8页
随着投掷次数的不断增多,石子落在图形 内的频率逐渐稳定在 0.4 左右,因此估计石子落在图形 内的概
率为 ;由此估计图形 的面积为 平方米.
16.如图,在平面直角坐标系 中,已知点 ,0 , , 0 ,其中 + = 2,抛物线 = 2 + +
> 0 经过点 和 ,以下四个结论:① > 0;②3 + > 0;③关于 的一
元二次方程 2 + + 2 = 0 无实根;④点 1, 1 , 2, 2 在抛物线上且在对
称轴的同侧,当 1 2 = 2 ≥ 3 ≥
3
时,总有 1 2 时,则 4 .其中所有正确
结论的序号是 .
三、解答题(本题共 12 小题,共 68 分.第 17-22 题各 5分;第 23-26 题各 6 分;
第 27-28 题各 7分.)
17.计算: 245 + cos30 tan60 + ( 2025)0.
+5
18 < 3 .解不等式组: 2 .
3 4 > 2( + 1)
19.关于 的一元二次方程 2 + 3 + 2 = 0.
(1)求证:该方程总有两个实数根;
(2)若该方程的实数根均为非负数,求 的取值范围.
第 3页,共 8页
20.如图,菱形 的对角线 和 交于点 ,分别过点 、 作 // . // . 和 交于点 .
(1)求证:四边形 是矩形;
(2)连接 ,当∠ = 60 . = 2 3时,求 tan∠ 的值.
21.我国古代著作《管子 地员篇》中介绍了一种用数学运算获得“宫商角徽羽”五音的方法.研究发现,当
琴弦的长度比满足一定关系时,就可以弹奏出不同的乐音.例如,三根弦按长度从长到短排列分别奏出乐音
“ , , ”,需满足相邻弦长的倒数差相等.若最长弦为 15 个单位长,最短弦为 10 个单位长,求中
间弦的长度.
22.在平面直角坐标系 中,函数 = + ( ≠ 0)的图象经过点 ( 2, 2)和 (1,4).
(1)求该函数的解析式;
(2)当 > 2 1时,对于 的每一个值,函数 = 2 + 的值小于函数 = + ( ≠ 0)的值,直接写出 的取
值范围.
第 4页,共 8页
23.如图,在 中, = .求作:射线 ,使得 / / .
小靖同学的作法如下:
①以点 为圆心, 长为半径画圆,延长 交⊙ 于点 ;
②作∠ 的角平分线交⊙ 于点 ;
③作射线 .所以射线 即为所求.
请你依据小靖同学设计的尺规作图过程,完成下列问题:
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹)
(2)完成下面的证明
证明:连接 ,∵ = ,∴点 在⊙ 上.
∵ 是⊙ 的直径,∴ ∠ =______(______)(填推理依据)
∵ 平分∠ ,∴ ∠ = ∠ .∴ = ,
∴ ∠ = ∠ (______)(填推理依据).
∴ = ,∴ ⊥ . (______)(填推理依据).∴ // .
24.如图,⊙ 的直径 垂直弦 于点 , 是圆上一点, 是 的中点,连结 交 于点 ,连结 .
(1)求证: = .
(2)若 = 6, = 4,求 的长.
第 5页,共 8页
25.某兴趣小组通过实验研究发现:当音量 (单位: )满足 40 ≤ ≤ 70 时,听觉舒适度 与音量 之间满
足二次函数关系.当音量为 45 时,听觉舒适度为 6;当音量为 55 时,听觉舒适度达到最大值 10.
(1)求该二次函数的解析式,并在图 1 的平面直角坐标系中画出该二次函数的图象;
(2)在家听音乐时,小明听到的音量 与所坐位置到音箱的距离 (单位: )的关系如图 2 所示.若她希望听
觉舒适度不小于 9,根据此实验研究结果,请写出小明所坐位置到音箱的距离 的取值范围______(结果保
留小数点后一位).
26.在平面直角坐标系 中,二次函数 = 2 + + > 0 的图象经过点 2, .
(1)求此二次函数图象的对称轴;
(2)若二次函数 = 2 + + > 0 的图象上存在两点 1, 1 , 2, 2 ,其中 1 < 1 < , +
2 < 2 < + 4,且 1 = 2,求 的取值范围.
第 6页,共 8页
27.在 中,∠ = ∠ = 0 < < 45 , ⊥ 于点 , 是线段 上的动点(不与点 , ,
重合),将线段 绕点 顺时针旋转 2 得到线段 .
(1)如图 1,如果点 在线段 上,求证: ⊥ ;
(2)如图 2,如果 在线段 上,在射线 上存在点 满足 = ,连接 , , ,求证: ⊥ .
第 7页,共 8页
28.在平面直角坐标系 中,⊙ 的半径为 2,对于点 , 和⊙ 的弦 ,给出如下定义:若弦 上存
在点 ,使得点 绕点 逆时针旋转 60 后与点 重合,则称点 是点 关于弦 的“等边旋转点”.
(1)如图,点 2,0 ,直线 = 1 与⊙ 交于点 , .
①点 的坐标为______,点 ______(填“是”或“不是”)点 关于弦 的“等边旋转点”;
②若点 关于弦 的“等边旋转点”为点 ,则 的最小值为______,当 与⊙ 相切时,点 的坐标为
______;
(2)已知点 , 0 , 1,0 ,若对于线段 上的每一点 ,都存在⊙ 的长为 2 3的弦 ,使得点 是点
关于弦 的“等边旋转点”,直接写出 的取值范围.
第 8页,共 8页
姓名: 班级:
一、选择题(本题共 8 小题,每小题 2 分,共 16 分。在每小题给出的选项中,只有一项是符合题目要求的)
1.下列巴黎奥运会项目标志中,既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
2.若 = 2 是关于 的一元二次方程 2 + = 0 的一个解,则 的值为( )
A. 2 B. 4 C. 2 D. 4
3.抛物线 = + 2 2 1 的对称轴是( )
A. = 2 B. = 2 C. = 1 D. = 1
4.如图, 是⊙ 的直径,点 在 的延长线上, 切⊙ 于点 ,如果∠ = 30 , = 4,那么 的
长是( )
A. 6 B. 4 C. 2 3 D. 3
第 6 题图
第 4 题图
5.点 1, 1 , 2, 2 在抛物线 =
1 22 1 上,则 1, 2的大小关系是( )
A. 1 < 2 B. 1 > 2 C. 1 = 2 D.无法判断
6.为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图,架在消防车上的云梯 可伸缩,也可
绕点 转动,其底部 离地面的距离 为 2 ,当云梯顶端 在建筑物 所在直线上时,底部 到 的距离
为 10 ,若∠ = ,则此时云梯顶端 离地面的高度 的长是( )
A. 10tan + 2 B. 10tan + 2 C.
10
cos + 2 D. 10sin + 2
7.我国新能源汽车产业为应对全球气候变化、推动低碳发展做出了巨大贡献.根据中国汽车工业协会发布
的数据,2024 年 5 月新能源汽车销量约为 95.5 万辆,2024 年 7 月新能源汽车销量约为 99.1 万辆,设新
能源汽车销量的月平均增长率为 ,则 满足的方程是( )
A. 95.5 1 + 2 = 99.1 B. 95.5 1 + 2 2 = 99.1 C. 95.5 1 + 2 = 99.1 D. 95.5 1 + 2 = 99.1
第 1页,共 8页
8.如图,已知⊙ 及⊙ 外一定点 ,嘉嘉进行了如下操作后,得出了四个结论:
①点 是 的中点;②直线 , 都是⊙ 的切线;③点 到点 、点 的距离相等;
④连接 , , , 1, ,则 △ = 8 四边形 .对上述结论描述正确的是( )
A.只有①正确 B. 只有②正确 C.①②③正确 D.①②③④都正确
二、填空题(本题共 8 小题,每小题 2 分,共 16 分)
9.若 3在实数范围内有意义,则实数 的取值范围为 .
10.分解因式: 2 4 = ______.
11.已知二次函数满足条件:①有最大值;②它的图象经过点 1,0 ,写出一个满足上述所有条件的二次函
数的解析式 .
12.如图, 、 是 边 、 上的两点,且 // , : = 1: 3,那么 : = .
第 12 题图 第 13 题图 第 14 题图
13.图 1 为一个装有液体的圆底烧瓶(厚度忽略不计),侧面示意图如图 2,其液体水平宽度 为 16 ,竖
直高度 为 4 ,则⊙ 的半径为 .
14.如图, 是⊙ 的直径, , 是⊙ 的切线,切点分别为 , .若 = 2,∠ = 60 ,则 的
长是 .
15.小明看到公园地面上有一个心形封闭图形 ,为了研究图形 的面积,设计了一项试验:在图形 外部
绘制一个半径为 1 米的圆,如图所示,向这个圆内随机投掷石子.假设石子落在圆内的每一点都是等可能
的(不考虑边界),记录的试验数据如下:
掷石子的总次数 50100200500…
石子落在图形 内的次数 1543 80 201…
石子落在阴影部分的次数 3557 120299…
第 2页,共 8页
随着投掷次数的不断增多,石子落在图形 内的频率逐渐稳定在 0.4 左右,因此估计石子落在图形 内的概
率为 ;由此估计图形 的面积为 平方米.
16.如图,在平面直角坐标系 中,已知点 ,0 , , 0 ,其中 + = 2,抛物线 = 2 + +
> 0 经过点 和 ,以下四个结论:① > 0;②3 + > 0;③关于 的一
元二次方程 2 + + 2 = 0 无实根;④点 1, 1 , 2, 2 在抛物线上且在对
称轴的同侧,当 1 2 = 2 ≥ 3 ≥
3
时,总有 1 2 时,则 4 .其中所有正确
结论的序号是 .
三、解答题(本题共 12 小题,共 68 分.第 17-22 题各 5分;第 23-26 题各 6 分;
第 27-28 题各 7分.)
17.计算: 245 + cos30 tan60 + ( 2025)0.
+5
18 < 3 .解不等式组: 2 .
3 4 > 2( + 1)
19.关于 的一元二次方程 2 + 3 + 2 = 0.
(1)求证:该方程总有两个实数根;
(2)若该方程的实数根均为非负数,求 的取值范围.
第 3页,共 8页
20.如图,菱形 的对角线 和 交于点 ,分别过点 、 作 // . // . 和 交于点 .
(1)求证:四边形 是矩形;
(2)连接 ,当∠ = 60 . = 2 3时,求 tan∠ 的值.
21.我国古代著作《管子 地员篇》中介绍了一种用数学运算获得“宫商角徽羽”五音的方法.研究发现,当
琴弦的长度比满足一定关系时,就可以弹奏出不同的乐音.例如,三根弦按长度从长到短排列分别奏出乐音
“ , , ”,需满足相邻弦长的倒数差相等.若最长弦为 15 个单位长,最短弦为 10 个单位长,求中
间弦的长度.
22.在平面直角坐标系 中,函数 = + ( ≠ 0)的图象经过点 ( 2, 2)和 (1,4).
(1)求该函数的解析式;
(2)当 > 2 1时,对于 的每一个值,函数 = 2 + 的值小于函数 = + ( ≠ 0)的值,直接写出 的取
值范围.
第 4页,共 8页
23.如图,在 中, = .求作:射线 ,使得 / / .
小靖同学的作法如下:
①以点 为圆心, 长为半径画圆,延长 交⊙ 于点 ;
②作∠ 的角平分线交⊙ 于点 ;
③作射线 .所以射线 即为所求.
请你依据小靖同学设计的尺规作图过程,完成下列问题:
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹)
(2)完成下面的证明
证明:连接 ,∵ = ,∴点 在⊙ 上.
∵ 是⊙ 的直径,∴ ∠ =______(______)(填推理依据)
∵ 平分∠ ,∴ ∠ = ∠ .∴ = ,
∴ ∠ = ∠ (______)(填推理依据).
∴ = ,∴ ⊥ . (______)(填推理依据).∴ // .
24.如图,⊙ 的直径 垂直弦 于点 , 是圆上一点, 是 的中点,连结 交 于点 ,连结 .
(1)求证: = .
(2)若 = 6, = 4,求 的长.
第 5页,共 8页
25.某兴趣小组通过实验研究发现:当音量 (单位: )满足 40 ≤ ≤ 70 时,听觉舒适度 与音量 之间满
足二次函数关系.当音量为 45 时,听觉舒适度为 6;当音量为 55 时,听觉舒适度达到最大值 10.
(1)求该二次函数的解析式,并在图 1 的平面直角坐标系中画出该二次函数的图象;
(2)在家听音乐时,小明听到的音量 与所坐位置到音箱的距离 (单位: )的关系如图 2 所示.若她希望听
觉舒适度不小于 9,根据此实验研究结果,请写出小明所坐位置到音箱的距离 的取值范围______(结果保
留小数点后一位).
26.在平面直角坐标系 中,二次函数 = 2 + + > 0 的图象经过点 2, .
(1)求此二次函数图象的对称轴;
(2)若二次函数 = 2 + + > 0 的图象上存在两点 1, 1 , 2, 2 ,其中 1 < 1 < , +
2 < 2 < + 4,且 1 = 2,求 的取值范围.
第 6页,共 8页
27.在 中,∠ = ∠ = 0 < < 45 , ⊥ 于点 , 是线段 上的动点(不与点 , ,
重合),将线段 绕点 顺时针旋转 2 得到线段 .
(1)如图 1,如果点 在线段 上,求证: ⊥ ;
(2)如图 2,如果 在线段 上,在射线 上存在点 满足 = ,连接 , , ,求证: ⊥ .
第 7页,共 8页
28.在平面直角坐标系 中,⊙ 的半径为 2,对于点 , 和⊙ 的弦 ,给出如下定义:若弦 上存
在点 ,使得点 绕点 逆时针旋转 60 后与点 重合,则称点 是点 关于弦 的“等边旋转点”.
(1)如图,点 2,0 ,直线 = 1 与⊙ 交于点 , .
①点 的坐标为______,点 ______(填“是”或“不是”)点 关于弦 的“等边旋转点”;
②若点 关于弦 的“等边旋转点”为点 ,则 的最小值为______,当 与⊙ 相切时,点 的坐标为
______;
(2)已知点 , 0 , 1,0 ,若对于线段 上的每一点 ,都存在⊙ 的长为 2 3的弦 ,使得点 是点
关于弦 的“等边旋转点”,直接写出 的取值范围.
第 8页,共 8页
同课章节目录
