2025年福建厦门中考数学九年级下学期综合训练(二)(含答案)
文档属性
| 名称 | 2025年福建厦门中考数学九年级下学期综合训练(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 868.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-25 08:13:58 | ||
图片预览




文档简介
2025年中考九年级下学期春季综合训练(二)
基础综合题目+几何综合+二次函数综合+动点+反比例基础
(建议练习时间:120分钟 满分150分)
综合难度系数:☆☆☆☆
一、选择题:(每题4分,共48分)
1.☆下列各式中是分式方程的是
A. B.
C. D.
(解题要点:分式方程定义)
2.☆下列不是正方体表面展开图的是( )
(解题要点:展开图立体几何逆向思维)
3.☆下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形 B.对角线相等的平行四边形是矩形
C.对角线互相垂直平分的四边形是菱形 D.对角线相等且垂直的四边形是正方形
(解题要点:举出反例)
4.☆如图,=,与互补,则下列结论中错误的是( )
= =
= =
(解题要点:平行和相似的关系)
5.☆下列说法正确的是( )
五名学生在某次测体温时得到:36.2,36.3,36.3,36.5,36.5,这组数据的众数是36.5.
方差越大,数据的波动越大,方差越小,数据的波动越小.
确定性事件一定发生.
为了解一批灯泡的寿命,应采用全面调查方式.
6.☆如图,△ABC是锐角三角形,AD、AE、AF分别是△ABC的中线、角平分线、高线,则下列点一定在AE上的是( )
重心 内心 外心 垂心
(解题要点:各种“心”的定义)
7.☆☆如图,点是双曲线=(x>0)上的一点,=与=的图像关于y轴对称,过点A作AB//X轴交=的图像于点B,点C是x轴上一点,连接AC、BC,则△ABC的面积为( )
16 8 4 2
(解题要点:反比例还是K的几何意义)
8.☆若用科学记数法表示为1.8×10﹣12,则n的值是( )
10 11 12 13
☆☆如图,以扇形ACB上一点O为圆心作圆,使圆经过A、B、C三点,已知⊙O的半径是4,连接OB,∠OCB=60,若将扇形ABC剪下,围成一个圆锥,则此圆锥的底面积是( )
(解题要点:扇形面积的计算原始逻辑和圆锥的关系)
10.☆☆如图,在平行四边形ABCD中,AB=2.ABC=60,按以下步骤作图:①以B为圆心,AB长为半径画弧,交BC于点E;②分别以A、E为圆心,大于AE长为半径画弧,两弧交于点M; ③连接BM交AD于点F,过点A作AH⊥BF于点H,则BF的长是( )
4 3 2
11.☆☆如图,直线y=-2x+4与两坐标轴分别交于A、B两点,点C是直线AB上一点,且横坐标为-1,过点C的直线交x轴于点D,则三角形ADC的面积为( )
45 42 43 44
12.☆☆☆在平面直角坐标系中,图①是抛物线y=x(-1≤x≤4)的图象,现将图①绕原点O旋转180得到图②,若直线y=-x+m与图①、②有三个交点,则m的取值范围是()
-5≤m≤-1或1≤m≤5 -4≤m≤-1或1≤m≤4
-5≤m≤-2或2≤m≤5 -2≤m≤-4或2≤m≤4
(解题要点:二次函数画图的数形结合)
二、填空题(每题4分,共16分)
13.☆:_______
14.☆若一组数据5、6、x、9、10的平均数是8,则这组数据的中位数是_________
15.☆☆如图,在⊙O中,弦AB=2,于点,且OC=1,经过点C的直线交⊙O于点E、F且=60,OH⊥EF于点H,则EF弦的长是___________
(解题要点:垂径定理辅助线构造)
☆☆☆如图,在梯形ABCD中,BC//AD,=60,ADC=90,ACB=45,AB=4,点P是AC上一动点(不与A、C重合),连接DP,当AP+BC最小时,S=
(解题要点:胡不归模型)
解答题
☆☆☆(本题满分8分)
如图,在中,,延长到点D,,点E是的中点,交于点F,则的面积为 .
(解题要点:直角三角形的辅助线构造)
18.☆☆☆☆(本题满分8分)
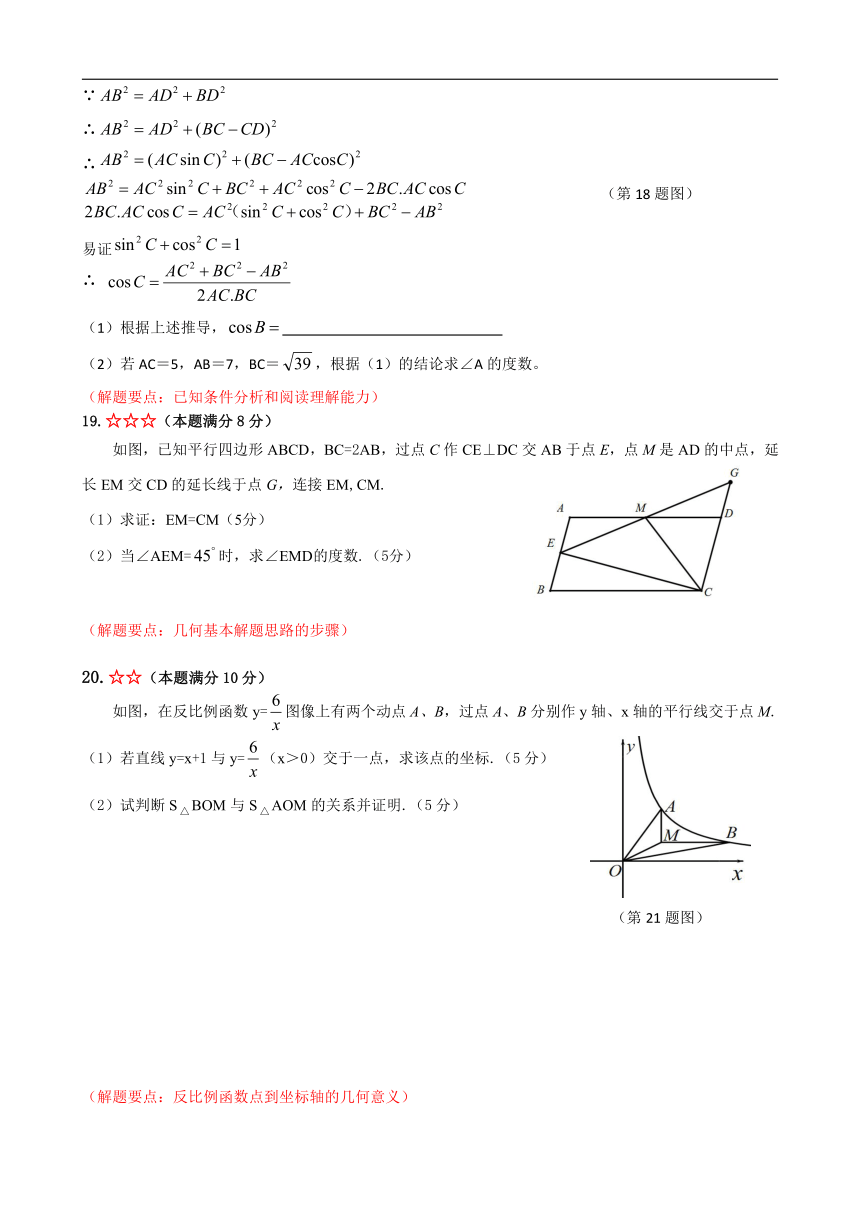
学习三角函数后,爱探究的小吴在锐角△ABC中作如下图推导:
解:过A作AD⊥BC于D,
∴ ,
∴ ,
∵
∴
∴
易证
∴
根据上述推导,
若AC=5,AB=7,BC=,根据(1)的结论求∠A的度数。
(解题要点:已知条件分析和阅读理解能力)
19.☆☆☆(本题满分8分)
如图,已知平行四边形ABCD,BC=2AB,过点C作CE⊥DC交AB于点E,点M是AD的中点,延长EM交CD的延长线于点G,连接EM,CM.
求证:EM=CM(5分)
当∠AEM=时,求∠EMD的度数.(5分)
(解题要点:几何基本解题思路的步骤)
20.☆☆(本题满分10分)
如图,在反比例函数y=图像上有两个动点A、B,过点A、B分别作y轴、x轴的平行线交于点M.
(1)若直线y=x+1与y=(x>0)交于一点,求该点的坐标.(5分)
(2)试判断SBOM与SAOM的关系并证明.(5分)
(解题要点:反比例函数点到坐标轴的几何意义)
21.☆☆☆(本题满分10分)
在脱贫攻坚中,某县对城西学府家园某栋楼的100平方米和120平方米的两种规格套房进行装修。经预算,共需资金350万元。已知装修两套100平方米和三套120平方米的套房共用资金61万元,装修三套100平方米和五套120平方米的套房共用资金98万元.
(1)若已知该栋楼120平方米的套房不多于10套,则100平方米的套房至少有多少套?(5分)
(2)有一位爱心人士愿意捐款与政府一道对该栋楼的两种套房装修20套,若爱心捐款投入装修不多于150万元,政府投入装修不低于85万元,其中爱心捐款用于100平方米和120平方米的每套装修分别为7万元和8万元,试计算有多少种装修方案?写出计算过程.(5分)
(解题要点:根据已知条件构建等式关系和不等式关系)
22.☆☆某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
(解题要点:寻找相似关系,发现相同比例构建等式关系)
23.☆☆☆☆(本题满分10分)
如图:抛物线y=ax2+bx+c(a≠0)与x轴交于点A,B两点,OB:OA=1:3,与y轴交于点C,OA=OC=3,点G为抛物线的顶点.
(1)求这条抛物线的函数表达式;(4分)
(2)求△ADC的周长(4分)
(3)点P是抛物线上的一个动点,过点P作PE⊥X轴于点E,在抛物线上是否存在点P,使得△PAE与△OBC相似?若存在,求出点E的坐标,若不存在,请说明理由.(4分)
(解题要点:构建相似三角形,分多种情况讨论)
24.☆☆☆☆(本题满分10分)(解题要点:构建全等三角形)
(1)知识积累:如图①,∠ACB=∠AOB=,CA交OA于点A,CB交OB于点B,OC平分∠AOB,求证:AC=BC;(4分)
(2)知识迁移:如图②,∠AOB=120,∠ACB=60,CA交OA于点A,CB交OB于点B,OC平分∠AOB,判断线段OA、OB、OC三者之间的关系并证明;(4分)
(3)知识探索:如图③,∠AOB=2α,∠ACB=180-2α,CA交OA于点A,CB交OB于点B,AC=BC.
探索线段OA、OB、OC与α的关系并证明.当OA=(4分)
25.☆☆☆☆☆(12分)如图,抛物线与直线y=mx+n交于B(0,4),C(3,1)两点.直线与x轴交于点A,P为直线AB上方的抛物线上一点,连接PB,PO.
(1)求抛物线的解析式;
(2)如图1,连接PC,OC,△OPC和△OPB面积之比为1:2,求点P的坐标;
(3)如图2,PB交抛物线对称轴于M,PO交AB于N,连接MN,PA,当MNPA时,直接写出点P的坐标.
(解题要点:利用辅助线转换比例关系)
答案
1 2 3 4 5 6 7 8 9 10 11 12
C D D B B B C B D C A B
13.±√5 14.9 15.√15 16.2√3
17.答案:
解:∵,,
∴,
∵点E是的中点,
∴,
取的中点,连接,则:,
∴,
∴,
∴,
∴,
∴;
故答案为:.
答案
据上述推导,(4分)
AC=5,AB=7,BC=,根据(1)的结论求∠A的度数。
由推导易得(6分)
∵ AC=5,AB=7,BC=
∴(8分)
答案
.证明:(1)如图
∵四边形ABCD是平行四边形,点M是线段AD中点
∴AM=DM,AB∥CD
延长EM与CD的延长线交于点G (1分)
∴AB∥CG,∴∠1=∠AEM
∵∠5=∠6
∴△AEM≌△DGM(AAS)(3分)
∴EM=GM
又∵EC⊥CD
∴△EGC是直角三角形
∴EM=CM
∴∠4=∠8
∴EM=CM (5分)
(2)由(1)可知△AEM≌△DGM,△EGC是直角三角形,且点M是斜边中点
∴∠1=∠AEM=∠3 (6分)
在平行四边形ABCD中
∵BC=2AB
∴CD=MD
∴∠2=∠3
在△MGC中,∠EMC=∠1+∠3
∴∠EMD=3∠AEM(8分)
当∠AEM=45时,∠EMD=3∠AEM=3×45=135(10分)
答案
(1)由题可知,直线y=x+1与y=(x>0)交于一点
∴x+1=(1分)
解得x=2,x=-3(舍去)(3分)
∴当x=2时,y=x+1=2+1=3
∴该点坐标为(2,3)(5分)
(2)根据题意可知:AM∥y轴,BM∥x轴,A、B两动点在y=(x>0)的图像上
设点M坐标为(a,b)(6分)
∴点A坐标为(a,),点B坐标为()(7分)
∴SAOM=(8分)
∴SBOM=(9分)
∴SAOM=SBOM(10分)
答案
解:(1)设装修一套100平方米的套房用资金万元,装修一套120平方米的套房用资金万元,由题意得:
2x+3y=61
3x+5y=98 (2分)
解得 x=11
y=13 (3分)
设100平方米的套房至少有套,由题意得
11+1310≥350
解得≥20
答:100平方米的套房至少有20套。(6分)
(2)设装修100平方米的套房共套,则装修120平方米的套房共套,由题意得
7b+8(20﹣b)≤150
(11-7)b+(13-8)(20 - b)≥85 (9分)
解得10≤b≤15
∴共有6种装修方案。(12分)
22.答案:
(1)作图见试题解析;(2)1.5m/s.
(1)如图,
(2)设小明原来的速度为xm/s,
则CE=2xm,AM=AF﹣MF=(4x﹣1.2)m,
EG=2×1.5x=3xm,
BM=AB﹣AM=12﹣(4x﹣1.2)=13.2﹣4x,
∵点C,E,G在一条直线上,CG∥AB,
∴△OCE∽△OAM,△OEG∽△OMB,
∴,,
∴,
即,
解得x=1.5,经检验x=1.5为方程的解,
∴小明原来的速度为1.5m/s.
23.答案
(本题满分10分)
解:(1)由题可得:OA=OC=3
∴点A的坐标为(-3,0),点C的坐标为(0,-3)
∵OB:OA=1:3
∴点B的坐标为(1,0) (2分)
设抛物线解析式为:
把A、B、C三点坐标代入得:
解得:a=1,b=2,c=-3
∴抛物线解析式为: (4分)
(2)∵OA=OC=3
∴AC=
由
∴点D坐标为(-1,-4) (6分)
∴AD=
CD=
∴三角形ADC周长= (8分)
存在,理由如下: (9分)
设点P坐标为
如图:当△AEP∽△BOC时:
∴
解得:
如图:当△AEP∽△COB时:
∴
解得:
综上可得P的坐标为或或 (12分)
答案
解:
(1)如图①,过点C作CE⊥OB于点E,过点C作CF⊥OA的延长线于点F.
∴∠CFA=∠CEB=90 (1分)
∵OC平分∠AOB,∴CF=CE
在四边形AOBC中,∠AOB=∠ACB=90,∴∠CAO+∠CBO=180 (2分)
又∵∠CAO+∠CAF=180,∴∠CAF=∠CBO
∴△CAF≌△CBE(AAS)
∴AC=BC (4分)
(2).如图②,过点C作CG⊥OB的延长线于点G,过点C作CH⊥OA的于点H.
∴∠CHA=∠CGB=90
∵OC平分∠AOB,∴CH=CG (5分)
在四边形AOBC中,∵∠AOB=120,∠ACB=60
∴∠AOB+∠ACB=180,∴∠CAO+∠CBO=180
又∵∠CBG+∠CBO=180,∴∠CBG=∠CAH
∴△CAH≌△CBG(AAS)
∴AH=BG
又∵OC平分∠AOB,CG⊥OB的延长线于点G,CH⊥OA的于点H.
∴△HCO≌△GCO(AAS)(6分)
∴HO=GO
∴HO=OB+BG
∴AO+BO=2GO
在RtOGC中,∠COG=60
∴∠OCG=30,∴OC=2GO,∴AO+BO=OC.(8分)
(3)如图③,过点C作CN⊥OA的延长线于点N,过点C作CM⊥OA的于点M.
∴∠CNA=∠CMB=90
在四边形AOBC中,∵∠AOB=2α,∠ACB=180-2α
∴∠AOB+∠ACB=180,
∴∠CAO+∠CBO=180
又∵∠CAN+∠CAO=180,
∴∠CBO=∠CAN
∵CA=CB
∴△CAN≌△CBM(AAS)(10分)
∴MB=AN,CN=CM
∴OC平分∠AOB
∴∠COM=∠COA=α
易得:△CON≌△COM
∴OM=ON
∴AO+OB=2OM
在三角形OCM中,COSα .2OC=.2OC=2OM
∴OA+OB=2OC·COSα
∴COSα=
当OA=
COSα=
25.答案:
(1)抛物线的解析式为:;(2)点P的坐标为:(,);(3)点P的坐标为:(,)
【分析】(1)直接将B(0,4),C(3,1)代入,解方程组即可;
(2)待定系数法求BC的解析式为,OC解析式为,设P(,),由△OPC和△OPB面积之比为1:2,可得关于m的方程,求解即可得点P的坐标;
(3)过点P作PD⊥y轴于点D,交抛物线对称轴于点E,过点N作NF⊥y轴于点F,设点P(,),根据相似三角形性质可得方程求解即可.
【详解】(1)B(0,4),C(3,1)代入,
得:,
解得:,
∴抛物线的解析式为:;
(2)B(0,4),C(3,1)代入,
得:,
解得:,
可得m=-1,n=4,
∴直线BC的解析式为:,
同理可求直线OC解析式为:,
∵P为直线AB上方的抛物线上一点,
设P(,),则,
过点P作PD⊥y轴于D,作PF⊥x轴于F,交OC于G,过C作CE⊥x轴于E,
∴G(,),E(3,0),
∴PD=m,PG=(),OE=3,
S△OBP=OB PD=2m,
S△OPC=OE PG,
∵△OPC和△OPB面积之比为1:2,
∴,
整理得:,
解得:(舍去),
,
∴点P的坐标为:(,);
(3)∵,
∴抛物线对称轴为直线,
如图2,过点P作PD⊥y轴于点D,交抛物线对称轴于点E,过点N作NF⊥y轴于点F,
设点P(,),则DP=, DE=1,PE,
同理可得直线OP解析式为:,
联立方程组,
解得:,
∴FN=,
∵MN∥PA,
∴,
∵ME∥y轴,
∴,
∵FN∥x轴,
∴,
∴,即:DE OA=FN DP,
∴,
解得:(舍去),
,
∴点P的坐标为:(,).
基础综合题目+几何综合+二次函数综合+动点+反比例基础
(建议练习时间:120分钟 满分150分)
综合难度系数:☆☆☆☆
一、选择题:(每题4分,共48分)
1.☆下列各式中是分式方程的是
A. B.
C. D.
(解题要点:分式方程定义)
2.☆下列不是正方体表面展开图的是( )
(解题要点:展开图立体几何逆向思维)
3.☆下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形 B.对角线相等的平行四边形是矩形
C.对角线互相垂直平分的四边形是菱形 D.对角线相等且垂直的四边形是正方形
(解题要点:举出反例)
4.☆如图,=,与互补,则下列结论中错误的是( )
= =
= =
(解题要点:平行和相似的关系)
5.☆下列说法正确的是( )
五名学生在某次测体温时得到:36.2,36.3,36.3,36.5,36.5,这组数据的众数是36.5.
方差越大,数据的波动越大,方差越小,数据的波动越小.
确定性事件一定发生.
为了解一批灯泡的寿命,应采用全面调查方式.
6.☆如图,△ABC是锐角三角形,AD、AE、AF分别是△ABC的中线、角平分线、高线,则下列点一定在AE上的是( )
重心 内心 外心 垂心
(解题要点:各种“心”的定义)
7.☆☆如图,点是双曲线=(x>0)上的一点,=与=的图像关于y轴对称,过点A作AB//X轴交=的图像于点B,点C是x轴上一点,连接AC、BC,则△ABC的面积为( )
16 8 4 2
(解题要点:反比例还是K的几何意义)
8.☆若用科学记数法表示为1.8×10﹣12,则n的值是( )
10 11 12 13
☆☆如图,以扇形ACB上一点O为圆心作圆,使圆经过A、B、C三点,已知⊙O的半径是4,连接OB,∠OCB=60,若将扇形ABC剪下,围成一个圆锥,则此圆锥的底面积是( )
(解题要点:扇形面积的计算原始逻辑和圆锥的关系)
10.☆☆如图,在平行四边形ABCD中,AB=2.ABC=60,按以下步骤作图:①以B为圆心,AB长为半径画弧,交BC于点E;②分别以A、E为圆心,大于AE长为半径画弧,两弧交于点M; ③连接BM交AD于点F,过点A作AH⊥BF于点H,则BF的长是( )
4 3 2
11.☆☆如图,直线y=-2x+4与两坐标轴分别交于A、B两点,点C是直线AB上一点,且横坐标为-1,过点C的直线交x轴于点D,则三角形ADC的面积为( )
45 42 43 44
12.☆☆☆在平面直角坐标系中,图①是抛物线y=x(-1≤x≤4)的图象,现将图①绕原点O旋转180得到图②,若直线y=-x+m与图①、②有三个交点,则m的取值范围是()
-5≤m≤-1或1≤m≤5 -4≤m≤-1或1≤m≤4
-5≤m≤-2或2≤m≤5 -2≤m≤-4或2≤m≤4
(解题要点:二次函数画图的数形结合)
二、填空题(每题4分,共16分)
13.☆:_______
14.☆若一组数据5、6、x、9、10的平均数是8,则这组数据的中位数是_________
15.☆☆如图,在⊙O中,弦AB=2,于点,且OC=1,经过点C的直线交⊙O于点E、F且=60,OH⊥EF于点H,则EF弦的长是___________
(解题要点:垂径定理辅助线构造)
☆☆☆如图,在梯形ABCD中,BC//AD,=60,ADC=90,ACB=45,AB=4,点P是AC上一动点(不与A、C重合),连接DP,当AP+BC最小时,S=
(解题要点:胡不归模型)
解答题
☆☆☆(本题满分8分)
如图,在中,,延长到点D,,点E是的中点,交于点F,则的面积为 .
(解题要点:直角三角形的辅助线构造)
18.☆☆☆☆(本题满分8分)
学习三角函数后,爱探究的小吴在锐角△ABC中作如下图推导:
解:过A作AD⊥BC于D,
∴ ,
∴ ,
∵
∴
∴
易证
∴
根据上述推导,
若AC=5,AB=7,BC=,根据(1)的结论求∠A的度数。
(解题要点:已知条件分析和阅读理解能力)
19.☆☆☆(本题满分8分)
如图,已知平行四边形ABCD,BC=2AB,过点C作CE⊥DC交AB于点E,点M是AD的中点,延长EM交CD的延长线于点G,连接EM,CM.
求证:EM=CM(5分)
当∠AEM=时,求∠EMD的度数.(5分)
(解题要点:几何基本解题思路的步骤)
20.☆☆(本题满分10分)
如图,在反比例函数y=图像上有两个动点A、B,过点A、B分别作y轴、x轴的平行线交于点M.
(1)若直线y=x+1与y=(x>0)交于一点,求该点的坐标.(5分)
(2)试判断SBOM与SAOM的关系并证明.(5分)
(解题要点:反比例函数点到坐标轴的几何意义)
21.☆☆☆(本题满分10分)
在脱贫攻坚中,某县对城西学府家园某栋楼的100平方米和120平方米的两种规格套房进行装修。经预算,共需资金350万元。已知装修两套100平方米和三套120平方米的套房共用资金61万元,装修三套100平方米和五套120平方米的套房共用资金98万元.
(1)若已知该栋楼120平方米的套房不多于10套,则100平方米的套房至少有多少套?(5分)
(2)有一位爱心人士愿意捐款与政府一道对该栋楼的两种套房装修20套,若爱心捐款投入装修不多于150万元,政府投入装修不低于85万元,其中爱心捐款用于100平方米和120平方米的每套装修分别为7万元和8万元,试计算有多少种装修方案?写出计算过程.(5分)
(解题要点:根据已知条件构建等式关系和不等式关系)
22.☆☆某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
(解题要点:寻找相似关系,发现相同比例构建等式关系)
23.☆☆☆☆(本题满分10分)
如图:抛物线y=ax2+bx+c(a≠0)与x轴交于点A,B两点,OB:OA=1:3,与y轴交于点C,OA=OC=3,点G为抛物线的顶点.
(1)求这条抛物线的函数表达式;(4分)
(2)求△ADC的周长(4分)
(3)点P是抛物线上的一个动点,过点P作PE⊥X轴于点E,在抛物线上是否存在点P,使得△PAE与△OBC相似?若存在,求出点E的坐标,若不存在,请说明理由.(4分)
(解题要点:构建相似三角形,分多种情况讨论)
24.☆☆☆☆(本题满分10分)(解题要点:构建全等三角形)
(1)知识积累:如图①,∠ACB=∠AOB=,CA交OA于点A,CB交OB于点B,OC平分∠AOB,求证:AC=BC;(4分)
(2)知识迁移:如图②,∠AOB=120,∠ACB=60,CA交OA于点A,CB交OB于点B,OC平分∠AOB,判断线段OA、OB、OC三者之间的关系并证明;(4分)
(3)知识探索:如图③,∠AOB=2α,∠ACB=180-2α,CA交OA于点A,CB交OB于点B,AC=BC.
探索线段OA、OB、OC与α的关系并证明.当OA=(4分)
25.☆☆☆☆☆(12分)如图,抛物线与直线y=mx+n交于B(0,4),C(3,1)两点.直线与x轴交于点A,P为直线AB上方的抛物线上一点,连接PB,PO.
(1)求抛物线的解析式;
(2)如图1,连接PC,OC,△OPC和△OPB面积之比为1:2,求点P的坐标;
(3)如图2,PB交抛物线对称轴于M,PO交AB于N,连接MN,PA,当MNPA时,直接写出点P的坐标.
(解题要点:利用辅助线转换比例关系)
答案
1 2 3 4 5 6 7 8 9 10 11 12
C D D B B B C B D C A B
13.±√5 14.9 15.√15 16.2√3
17.答案:
解:∵,,
∴,
∵点E是的中点,
∴,
取的中点,连接,则:,
∴,
∴,
∴,
∴,
∴;
故答案为:.
答案
据上述推导,(4分)
AC=5,AB=7,BC=,根据(1)的结论求∠A的度数。
由推导易得(6分)
∵ AC=5,AB=7,BC=
∴(8分)
答案
.证明:(1)如图
∵四边形ABCD是平行四边形,点M是线段AD中点
∴AM=DM,AB∥CD
延长EM与CD的延长线交于点G (1分)
∴AB∥CG,∴∠1=∠AEM
∵∠5=∠6
∴△AEM≌△DGM(AAS)(3分)
∴EM=GM
又∵EC⊥CD
∴△EGC是直角三角形
∴EM=CM
∴∠4=∠8
∴EM=CM (5分)
(2)由(1)可知△AEM≌△DGM,△EGC是直角三角形,且点M是斜边中点
∴∠1=∠AEM=∠3 (6分)
在平行四边形ABCD中
∵BC=2AB
∴CD=MD
∴∠2=∠3
在△MGC中,∠EMC=∠1+∠3
∴∠EMD=3∠AEM(8分)
当∠AEM=45时,∠EMD=3∠AEM=3×45=135(10分)
答案
(1)由题可知,直线y=x+1与y=(x>0)交于一点
∴x+1=(1分)
解得x=2,x=-3(舍去)(3分)
∴当x=2时,y=x+1=2+1=3
∴该点坐标为(2,3)(5分)
(2)根据题意可知:AM∥y轴,BM∥x轴,A、B两动点在y=(x>0)的图像上
设点M坐标为(a,b)(6分)
∴点A坐标为(a,),点B坐标为()(7分)
∴SAOM=(8分)
∴SBOM=(9分)
∴SAOM=SBOM(10分)
答案
解:(1)设装修一套100平方米的套房用资金万元,装修一套120平方米的套房用资金万元,由题意得:
2x+3y=61
3x+5y=98 (2分)
解得 x=11
y=13 (3分)
设100平方米的套房至少有套,由题意得
11+1310≥350
解得≥20
答:100平方米的套房至少有20套。(6分)
(2)设装修100平方米的套房共套,则装修120平方米的套房共套,由题意得
7b+8(20﹣b)≤150
(11-7)b+(13-8)(20 - b)≥85 (9分)
解得10≤b≤15
∴共有6种装修方案。(12分)
22.答案:
(1)作图见试题解析;(2)1.5m/s.
(1)如图,
(2)设小明原来的速度为xm/s,
则CE=2xm,AM=AF﹣MF=(4x﹣1.2)m,
EG=2×1.5x=3xm,
BM=AB﹣AM=12﹣(4x﹣1.2)=13.2﹣4x,
∵点C,E,G在一条直线上,CG∥AB,
∴△OCE∽△OAM,△OEG∽△OMB,
∴,,
∴,
即,
解得x=1.5,经检验x=1.5为方程的解,
∴小明原来的速度为1.5m/s.
23.答案
(本题满分10分)
解:(1)由题可得:OA=OC=3
∴点A的坐标为(-3,0),点C的坐标为(0,-3)
∵OB:OA=1:3
∴点B的坐标为(1,0) (2分)
设抛物线解析式为:
把A、B、C三点坐标代入得:
解得:a=1,b=2,c=-3
∴抛物线解析式为: (4分)
(2)∵OA=OC=3
∴AC=
由
∴点D坐标为(-1,-4) (6分)
∴AD=
CD=
∴三角形ADC周长= (8分)
存在,理由如下: (9分)
设点P坐标为
如图:当△AEP∽△BOC时:
∴
解得:
如图:当△AEP∽△COB时:
∴
解得:
综上可得P的坐标为或或 (12分)
答案
解:
(1)如图①,过点C作CE⊥OB于点E,过点C作CF⊥OA的延长线于点F.
∴∠CFA=∠CEB=90 (1分)
∵OC平分∠AOB,∴CF=CE
在四边形AOBC中,∠AOB=∠ACB=90,∴∠CAO+∠CBO=180 (2分)
又∵∠CAO+∠CAF=180,∴∠CAF=∠CBO
∴△CAF≌△CBE(AAS)
∴AC=BC (4分)
(2).如图②,过点C作CG⊥OB的延长线于点G,过点C作CH⊥OA的于点H.
∴∠CHA=∠CGB=90
∵OC平分∠AOB,∴CH=CG (5分)
在四边形AOBC中,∵∠AOB=120,∠ACB=60
∴∠AOB+∠ACB=180,∴∠CAO+∠CBO=180
又∵∠CBG+∠CBO=180,∴∠CBG=∠CAH
∴△CAH≌△CBG(AAS)
∴AH=BG
又∵OC平分∠AOB,CG⊥OB的延长线于点G,CH⊥OA的于点H.
∴△HCO≌△GCO(AAS)(6分)
∴HO=GO
∴HO=OB+BG
∴AO+BO=2GO
在RtOGC中,∠COG=60
∴∠OCG=30,∴OC=2GO,∴AO+BO=OC.(8分)
(3)如图③,过点C作CN⊥OA的延长线于点N,过点C作CM⊥OA的于点M.
∴∠CNA=∠CMB=90
在四边形AOBC中,∵∠AOB=2α,∠ACB=180-2α
∴∠AOB+∠ACB=180,
∴∠CAO+∠CBO=180
又∵∠CAN+∠CAO=180,
∴∠CBO=∠CAN
∵CA=CB
∴△CAN≌△CBM(AAS)(10分)
∴MB=AN,CN=CM
∴OC平分∠AOB
∴∠COM=∠COA=α
易得:△CON≌△COM
∴OM=ON
∴AO+OB=2OM
在三角形OCM中,COSα .2OC=.2OC=2OM
∴OA+OB=2OC·COSα
∴COSα=
当OA=
COSα=
25.答案:
(1)抛物线的解析式为:;(2)点P的坐标为:(,);(3)点P的坐标为:(,)
【分析】(1)直接将B(0,4),C(3,1)代入,解方程组即可;
(2)待定系数法求BC的解析式为,OC解析式为,设P(,),由△OPC和△OPB面积之比为1:2,可得关于m的方程,求解即可得点P的坐标;
(3)过点P作PD⊥y轴于点D,交抛物线对称轴于点E,过点N作NF⊥y轴于点F,设点P(,),根据相似三角形性质可得方程求解即可.
【详解】(1)B(0,4),C(3,1)代入,
得:,
解得:,
∴抛物线的解析式为:;
(2)B(0,4),C(3,1)代入,
得:,
解得:,
可得m=-1,n=4,
∴直线BC的解析式为:,
同理可求直线OC解析式为:,
∵P为直线AB上方的抛物线上一点,
设P(,),则,
过点P作PD⊥y轴于D,作PF⊥x轴于F,交OC于G,过C作CE⊥x轴于E,
∴G(,),E(3,0),
∴PD=m,PG=(),OE=3,
S△OBP=OB PD=2m,
S△OPC=OE PG,
∵△OPC和△OPB面积之比为1:2,
∴,
整理得:,
解得:(舍去),
,
∴点P的坐标为:(,);
(3)∵,
∴抛物线对称轴为直线,
如图2,过点P作PD⊥y轴于点D,交抛物线对称轴于点E,过点N作NF⊥y轴于点F,
设点P(,),则DP=, DE=1,PE,
同理可得直线OP解析式为:,
联立方程组,
解得:,
∴FN=,
∵MN∥PA,
∴,
∵ME∥y轴,
∴,
∵FN∥x轴,
∴,
∴,即:DE OA=FN DP,
∴,
解得:(舍去),
,
∴点P的坐标为:(,).
同课章节目录
