沪教版七年级数学下册试题 18.2腰三角形的判定(含答案)
文档属性
| 名称 | 沪教版七年级数学下册试题 18.2腰三角形的判定(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-02-25 13:16:34 | ||
图片预览

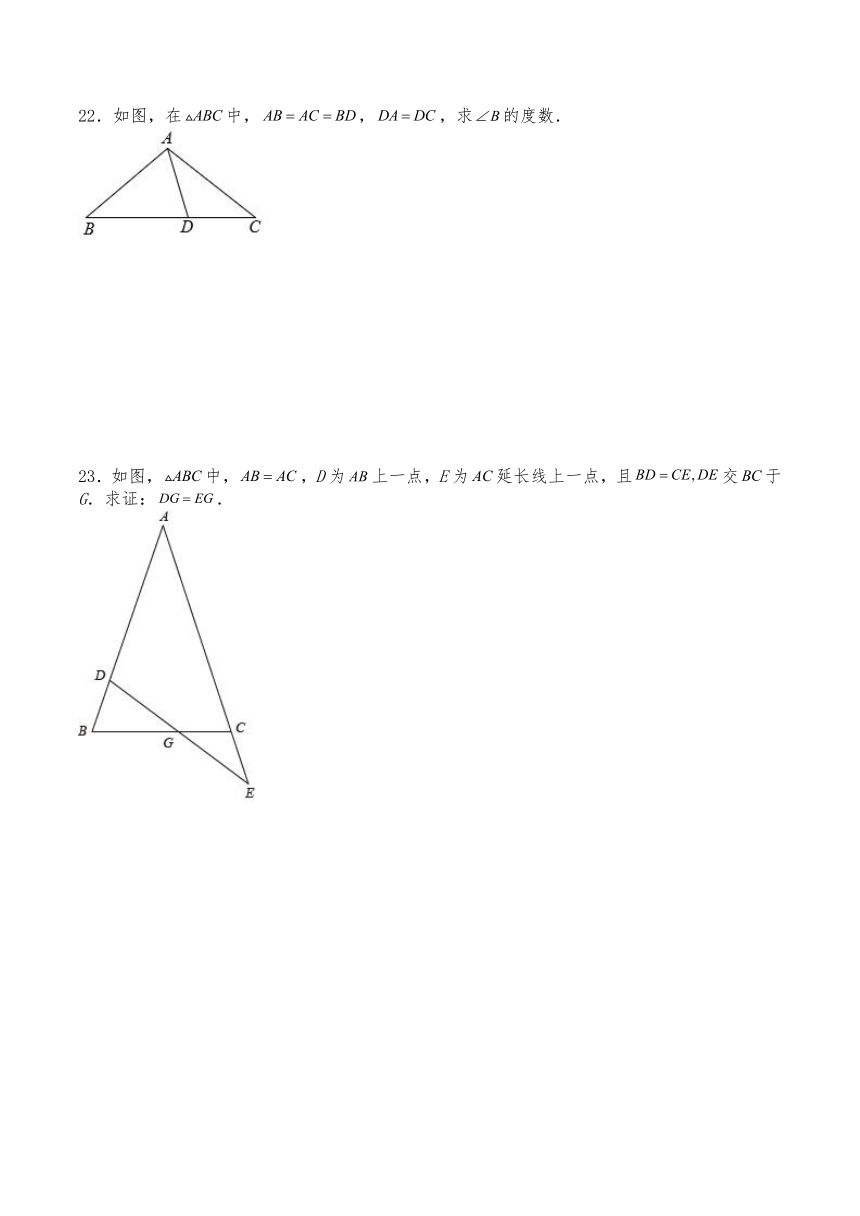
文档简介
18.2等腰三角形的判定
一、单选题
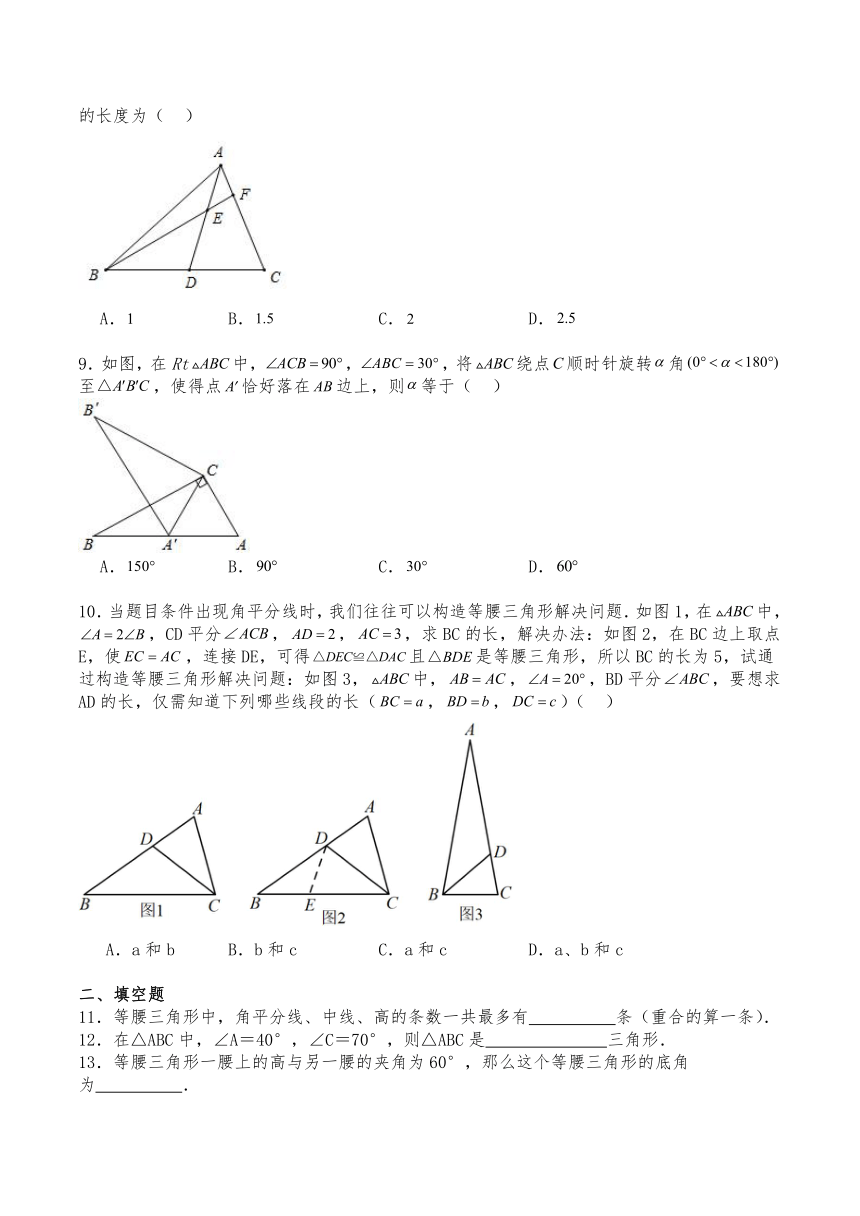
1.等腰三角形的一边等于3,一边等于6,则它的周长为( )
A.12 B.12或15 C.15或18 D.15
2.如图,中,,D是中点,下列结论中不正确的是( )
A. B. C.平分 D.
3.如图,中,,,则等于( )
A. B. C. D.
4.等腰三角形的一个角比另一个角2倍少20度,等腰三角形顶角的度数是( )
A.或或 B.或
C.或 D.或
5.下列能判定△ABC为等腰三角形的是( )
A.∠A=30°,∠B=60° B.∠A=50°,∠B=80°
C.∠A=2∠B=80° D.AB=3,BC=6,周长为13
6.已知是的两边,且,则的形状是( )
A.等腰三角形 B.等边三角形 C.锐角三角形 D.不确定
7.在等腰△ABC中,AB=AC,其周长为16cm,则AB边的取值范围是( )
A.1cm<AB<4cm B.3cm<AB<6cm
C.4cm<AB<8cm D.5cm<AB<10cm
8.如图,是的中线,是上一点,交于,若,则的长度为( )
A. B. C. D.
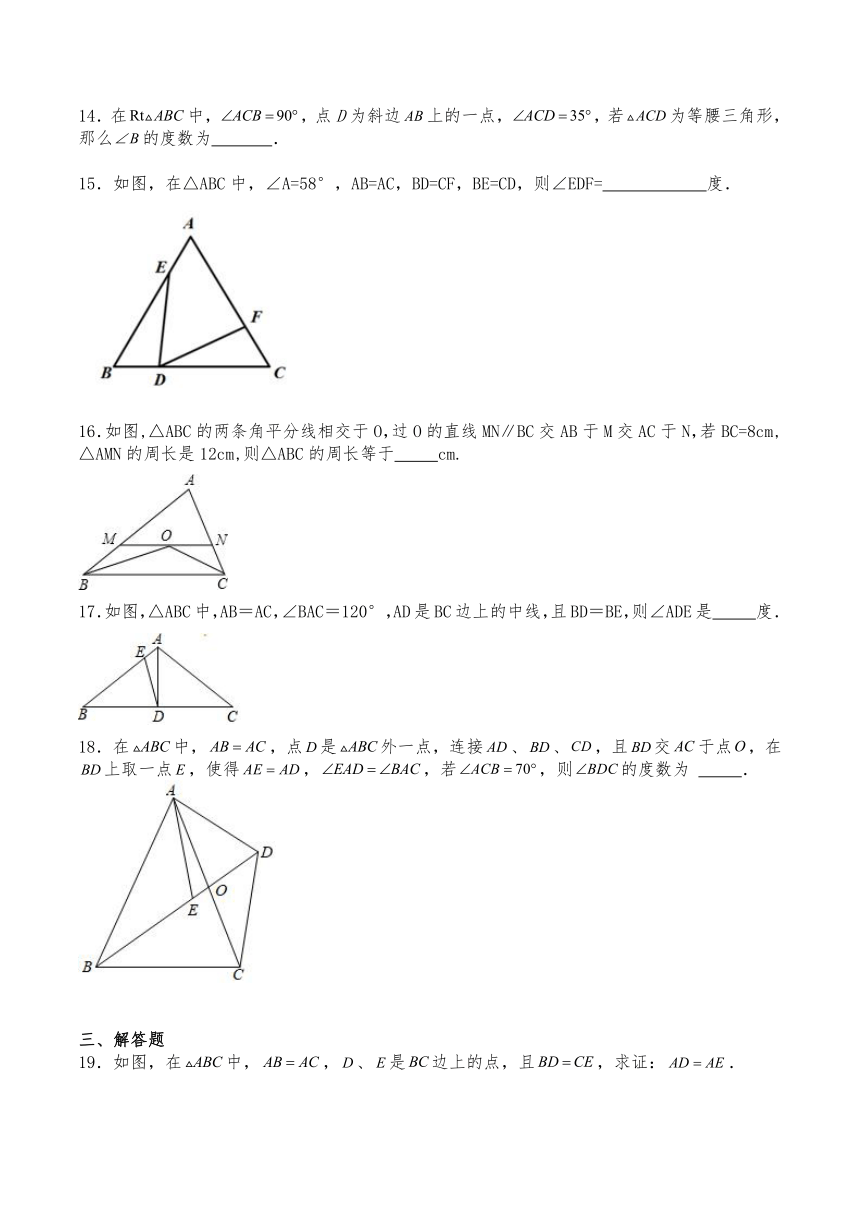
9.如图,在Rt中,,,将绕点顺时针旋转角至,使得点恰好落在边上,则等于( )
A. B. C. D.
10.当题目条件出现角平分线时,我们往往可以构造等腰三角形解决问题.如图1,在中,,CD平分,,,求BC的长,解决办法:如图2,在BC边上取点E,使,连接DE,可得且是等腰三角形,所以BC的长为5,试通过构造等腰三角形解决问题:如图3,中,,,BD平分,要想求AD的长,仅需知道下列哪些线段的长(,,)( )
A.a和b B.b和c C.a和c D.a、b和c
二、填空题
11.等腰三角形中,角平分线、中线、高的条数一共最多有 条(重合的算一条).
12.在△ABC中,∠A=40°,∠C=70°,则△ABC是 三角形.
13.等腰三角形一腰上的高与另一腰的夹角为60°,那么这个等腰三角形的底角为 .
14.在中,,点D为斜边上的一点,,若为等腰三角形,那么的度数为 .
15.如图,在△ABC中,∠A=58°,AB=AC,BD=CF,BE=CD,则∠EDF= 度.
16.如图,△ABC的两条角平分线相交于O,过O的直线MN∥BC交AB于M交AC于N,若BC=8cm,△AMN的周长是12cm,则△ABC的周长等于 cm.
17.如图,△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,且BD=BE,则∠ADE是 度.
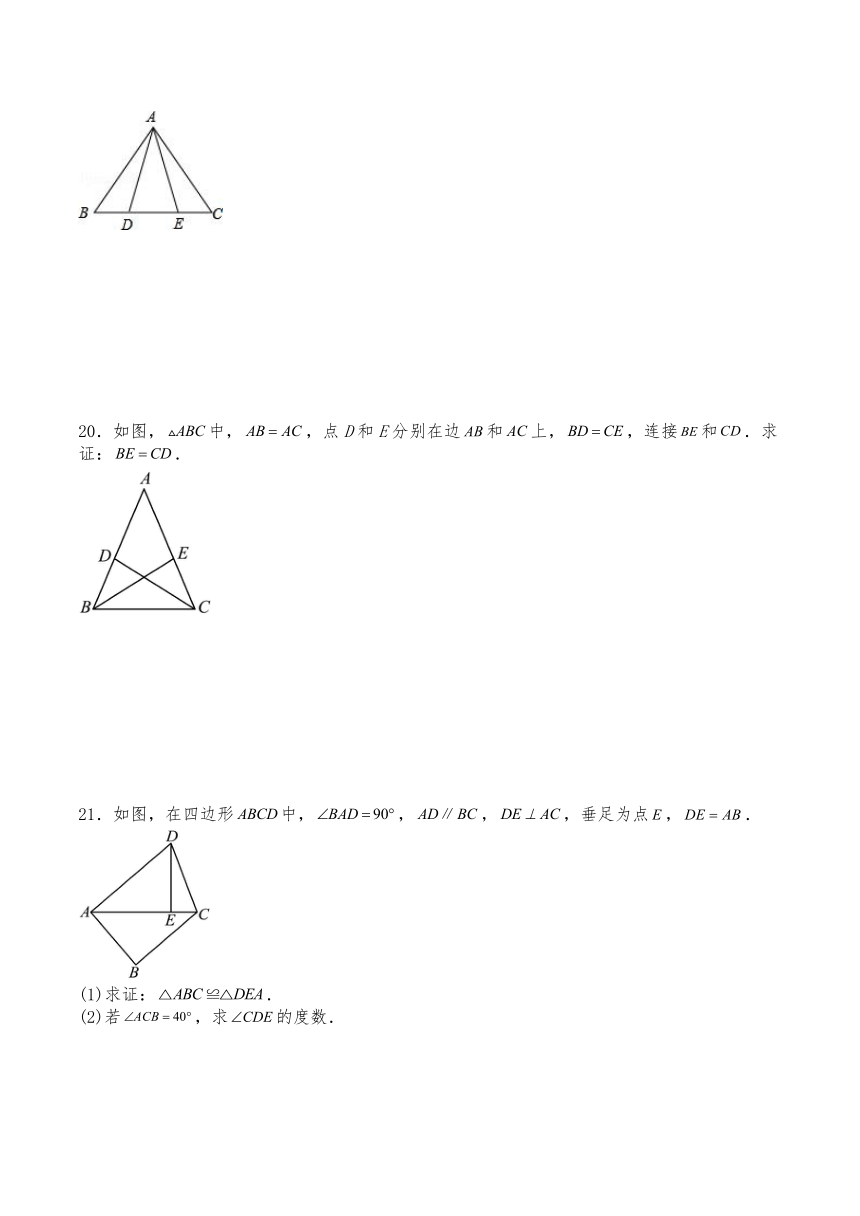
18.在中,,点是外一点,连接、、,且交于点,在上取一点,使得,,若,则的度数为 .
三、解答题
19.如图,在中,,、是边上的点,且,求证:.
20.如图,中,,点D和E分别在边和上,,连接和.求证:.
21.如图,在四边形中,,,,垂足为点,.
(1)求证:.
(2)若,求的度数.
22.如图,在中,,,求的度数.
23.如图,中,,D为上一点,E为延长线上一点,且交于G.求证:.
24.如图,在中,,点、、分别在、、边上,且,.
(1)求证:为等腰三角形;
(2)当时,求的度数.
25.如图,在中,AD平分,过点B作AD的垂线,垂足为点D,,交AB于点E,.
(1)求证:是等腰三角形;
(2)求证:.
26.如图,点在线段上,点在线段上,,,,,分别是,的中点.
(1)求证AE=CD
(2)连接MN,判断△MBN的形状,并证明
27.在中,,,将一块足够大的直角三角尺PMN(,)按如图所示放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角,斜边PN交AC于点D.
(1)当时,______度.
(2)在点P滑动的过程中,当AP的长度为多少时,与全等?说明理由.
(3)在点P滑动的过程中,的形状可以是等腰三角形吗?若不可以,请说明理由;若可以,请求出的大小.
28.如图,在中,,,,,三点共线,点在上,,,分别交于,两点.
(1)求证:;
(2)若.
①求证:;
②探究,与的数量关系,并证明.
答案
一、单选题
1.D
【分析】分别从若腰长为3,底边长为6,若腰长为6,底边长为3,去分析求解即可求得答案,注意三角形的三边关系.
【解析】解:①若腰长为3,底边长为6,
∵3+3=6,
∴不能组成三角形,舍去;
②若腰长为6,底边长为3,
则它的周长是:6+6+3=15.
∴它的周长是15,
故选:D.
2.D
【分析】利用三线合一的性质对每一个选项进行验证从而求解.
【解析】解:∵△ABC中,AB=AC,D是BC中点,
∴∠B=∠C,(故A正确)
AD⊥BC,(故B正确)
∠BAD=∠CAD(故C正确)
无法得到AB=2BD,(故D不正确).
故选:D.
3.A
【分析】利用AD=AC,求出∠ADC=∠C=,利用AD=AB,即可求得∠B=∠BAD.
【解析】∵AD=AC,
∴∠ADC=∠C,
∵,
∴∠ADC=∠C=,
∵AD=AB,
∴∠B=∠BAD,
故选:A.
4.A
【分析】设另一个角是x,表示出一个角是2x-20°,然后分①x是顶角,2x-20°是底角,②x是底角,2x-20°是顶角,③x与2x-20°都是底角根据三角形的内角和等于180°与等腰三角形两底角相等列出方程求解即可.
【解析】设另一个角是x,表示出一个角是2x﹣20°,
①x是顶角,2x﹣20°是底角时,x+2(2x﹣20°)=180°,
解得x=44°,
所以,顶角是44°;
②x是底角,2x﹣20°是顶角时,2x+(2x﹣20°)=180°,
解得x=50°,
所以,顶角是2×50°﹣20°=80°;
③x与2x﹣20°都是底角时,x=2x﹣20°,
解得x=20°,
所以,顶角是180°﹣20°×2=140°;
综上所述,这个等腰三角形的顶角度数是44°或80°或140°.
故选:A.
5.B
【分析】判断三角形中是否有相等的角,以及根据定义,是否有相等的边即可判断.
【解析】A、∠C=180° 30° 60°=90°,没有相等的角,则不是等腰三角形,A选项错误;
B、∠C=180° 50° 80°=50°,有相等的角,则是等腰三角形,B选项正确;
C、∵∠A=2∠B=80°,
∴∠B=40°,
∴∠C=60°,没有相等的角,则不是等腰三角形,C选项错误;
D、∵AB=3,BC=6,周长为13,
∴AC=13 6 3=4,没有相等的边,则不是等腰三角形,D选项错误;
故答案选:B.
6.A
【分析】把变形得到可得三角形形状.
【解析】解:因为:,所以:,
所以:,所以三角形ABC是等腰三角形,
故选A.
7.C
【分析】设AB=AC=x,则BC=16-2x,根据三角形的三边关系即可求出AB的取值范围.
【解析】在等腰△ABC中,AB=AC,其周长为16cm,
设设AB=AC=cm,则BC=16-2x,
依题意得,
解得4cm<AB<8cm,
选C.
8.B
【分析】延长AD到G使得,连接BG,证明,根据全等三角形的性质可得到,AC=BD,等量代换得到BE=BG,再由等腰三角形的性质得到,推出EF=AF,即可解决问题;
【解析】如图,延长AD到G使得,连接BG,
∵AD是△ABC的中线,
∴CD=BD,
在△ACD与△GBD中,
,
∴,
∴,AC=BD,
∵BE=AC,
∴BE=BG,
∴,
∵,
∴,
∴EF=AF,
∴,
即,
∴;
故选:B.
9.D
【分析】由旋转的性质可得CA=CA',∠ACA'=α,由等腰三角形的性质可得∠A=∠CA'A=60°,由三角形内角和定理可求α的值.
【解析】解:,,
,
将绕点顺时针旋转角至△,
,,
,
,
,
故选:.
10.A
【分析】在边上取点,使,连接,得到,在边上取点,使,连接,得到,即可推出结论.
【解析】解:要想求的长,仅需知道和的长,理由是:
如图4,中,,,
,
∵BD平分,
,,
在边上取点,使,连接,
在和中,
,
,
,
,
在边上取点,使,连接,
则,
,,
,
,
,
,
.
故选:A.
二、填空题
11.7
【分析】根据等腰三角形底边上三线合一的性质进行分析即可.
【解析】解:等腰三角形的角平分线,中线、高彼此重合的只计一条,即底边上的高、中线、角平分线只计一条,因此总条数最多有7条,故答案为7
12.等腰
【分析】根据三角形的内角和定理求出∠B,即可判断.
【解析】解:∵在△ABC中,∠A=40°,∠C=70°,
∴∠B=180°-∠A-∠C=70°
∴∠B=∠C
∴△ABC为等腰三角形
故答案为:等腰.
13.或
【分析】首先根据题意画出图形,然后分别从锐角三角形与钝角三角形分析求解即可求得答案.
【解析】解:根据题意得:AB=AC,BD⊥AC,
如图(1),∠ABD=60°,
则∠A=30°,
∴∠ABC=∠C=75°;
如图(2),∠ABD=60°,
∴∠BAD=30°,
∴∠ABC=∠C=∠BAD=15°.
故这个等腰三角形的底角是:75°或15°.
故答案为:或.
14.55°或
【分析】根据直角三角形的两个锐角互余可得∠A+∠B=90°,然后根据等腰三角形腰的情况分类讨论,分别画出对应的图形,根据等边对等角和三角形的内角和定理即可分别求出结论.
【解析】解:∵在中,,
∴∠A+∠B=90°
当DA=DC时,如下图所示
∴∠A=∠ACD=35°
∴∠B=90°-∠A=55°;
当CA=CD时,如下图所示
∴∠A=∠CDA=(180°-∠ACD)=
∴∠B=90°-∠A=;
当AC=AD时,
∴∠ADC=∠ACD=35°
∴∠A=180°-∠ADC-∠ACD=110°,不符合实际,舍去;
综上:的度数为55°或
故答案为:55°或.
15.61°
【分析】先由等腰三角形的性质求得∠B的大小,再证明△EBD≌△DFC,得到∠DEB=∠FDC;又由三角形内角和为∠BED+∠B+∠EDB=180°,即∠FDC+∠B+∠EDB=180°,可得∠FDC+∠EDB=180°-∠B由因为∠BDC是平角可得:∠EDF=180°-(∠FDC+∠EDB),即可完成作答.
【解析】解:∵等腰三角形ABC
∴
在△EBD和△DFC中
∴△EBD≌△DFC(AAS)
∴∠DEB=∠FDC
又∵在△EBD中,∠BED+∠B+∠EDB=180
∴∠FDC+∠EDB=180°-∠B=119°
又∵∠EDF+(∠FDC+∠EDB)=180°
∴∠EDF=180°-(∠FDC+∠EDB)= 180°-119°=61°
故答案为61°.
16.20
【分析】由已知条件根据平行线的性质、角平分线的性质及等角对等边可得MO=MB,NO=NC.从而根据△AMN的周长求出AB+AC,问题得解.
【解析】解:∵BO平分∠ABC,
∴∠ABO=∠OBC.
又∵MN∥BC,
∴∠MOB=∠OBC.
∴∠ABO=∠MOB,
∴MO=MB.
同理可得:NO=NC.
∴△AMN的周长为:AM+MN+AN=AM+MO+ON+AN=AM+MB+NC+AN=AB+AC=12cm,
∴△ABC的周长为:AB+AC+BC=12+8=20cm.
故答案为20.
17.15
【分析】根据等腰三角形的性质得到∠B=∠C=30°,∠ADB=90°,根据三角形内角和定理计算.
【解析】∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AB=AC,AD是BC边上的中线,
∴∠ADB=90°,
∵BD=BE,
∴∠BDE=75°,
∴∠ADE=15°,
故答案为15.
18.
【分析】根据证明,再利用全等三角形的性质,然后由三角形的外角性质,,可说明,再利用等腰三角形的性质可求出,最后利用三角形的内角和解答即可.
【解析】解:∵,
∴,
即,
在和中,
,
∴,
∴,
∵是和的外角,
∴,,
∴,
∴,
∵,,
∴,
∴,
∴.
故答案为:.
三、解答题
19.证明:∵,
∴,
在和中,
,
∴,
∴.
20.证明:,
∴,
在和中,
,
∴,
∴.
21.(1)证明:∵, ,
∴,,
∵,
∴∠AED=∠ABC=90°
∵,
∴;
(2)解:∵,
∴,,
∴∠ADC=∠ACD,
∴,
∵,
∴∠ADE+∠DAC=90°,
∴,
∴.
22.解:设,∵,∴,∵,∴,∴,∵,∴,在中,,,∴,解得,∴.
23.过点D作,交于F,
,
在与中
.
.
24.解:(1)∵,
∴,
在和中,
,
∴(),
∴,
∴为等腰三角形;
(2)∵,
∴,
∵是的外角,
∴,
∴,
∴,
在中,
∴,
∴.
25.(1)证明:如图,∵AD平分∠BAC,
∴∠1=∠2,
∵,CD∥AB,
∴.
∵,,
∴,
∴,
∴是等腰三角形;
(2)证明:由(1)得
∴,
∵,,,
∴,
∴,
∴.
26.(1)证明:(1)在和中,
,
∴.
∴AE=CD;
(2)是等腰直角三角形,理由如下:
连接MN,如图所示:
∵在(1)中已得,,
∴,,AE=DC,
∵M、N分别是AE、CD的中点,
∴,,
∴DN=AM,
又∵,,
∴,
∴BN=BM,,
∵,
∴,
∴是等腰直角三角形.
27.(1)解:当PNBC时,∠α=∠NPM=30°,
又∵∠ACB=120°,
∴∠ACP=120°﹣30°=90°,
故答案为:90;
(2)解:当AP=4时,△ADP≌△BPC,
理由为:∵∠ACB=120°,CA=CB,
∴∠A=∠B=30°,
又∵∠APC是△BPC的一个外角,
∴∠APC=∠B+∠α=30°+∠α,
∵∠APC=∠DPC+∠APD=30°+∠APD,
∴∠α=∠APD,
又∵AP=BC=4,
∴△ADP≌△BPC;
(3)解:的形状可以是等腰三角形.
由题意得,,
①当时,是等腰三角形,
∴,即,
∴.
②当时,是等腰三角形,
∴,
即,
∴.
③当时,是等腰三角形,
∴,
∴,
即,
∴,
此时点P与点B重合,点D和点A重合.
综上所述,当或90°或0°时,是等腰三角形.
28.(1)证明:,,
,
,
,
,
在与中,
,
;
(2)①证明:由(1)知,为等腰直角三角形,
,
,
,即,
,,
,
,
由(1)知,,
,
,
,
;
②,证明如下:
在上,取,连接,过点作交于点,
在与中,
,
,,,
,,三点共线,
,
,
为等腰直角三角形,即有,
,
,
,
,
,
,
,
,
,
在与中,
,
,
.
一、单选题
1.等腰三角形的一边等于3,一边等于6,则它的周长为( )
A.12 B.12或15 C.15或18 D.15
2.如图,中,,D是中点,下列结论中不正确的是( )
A. B. C.平分 D.
3.如图,中,,,则等于( )
A. B. C. D.
4.等腰三角形的一个角比另一个角2倍少20度,等腰三角形顶角的度数是( )
A.或或 B.或
C.或 D.或
5.下列能判定△ABC为等腰三角形的是( )
A.∠A=30°,∠B=60° B.∠A=50°,∠B=80°
C.∠A=2∠B=80° D.AB=3,BC=6,周长为13
6.已知是的两边,且,则的形状是( )
A.等腰三角形 B.等边三角形 C.锐角三角形 D.不确定
7.在等腰△ABC中,AB=AC,其周长为16cm,则AB边的取值范围是( )
A.1cm<AB<4cm B.3cm<AB<6cm
C.4cm<AB<8cm D.5cm<AB<10cm
8.如图,是的中线,是上一点,交于,若,则的长度为( )
A. B. C. D.
9.如图,在Rt中,,,将绕点顺时针旋转角至,使得点恰好落在边上,则等于( )
A. B. C. D.
10.当题目条件出现角平分线时,我们往往可以构造等腰三角形解决问题.如图1,在中,,CD平分,,,求BC的长,解决办法:如图2,在BC边上取点E,使,连接DE,可得且是等腰三角形,所以BC的长为5,试通过构造等腰三角形解决问题:如图3,中,,,BD平分,要想求AD的长,仅需知道下列哪些线段的长(,,)( )
A.a和b B.b和c C.a和c D.a、b和c
二、填空题
11.等腰三角形中,角平分线、中线、高的条数一共最多有 条(重合的算一条).
12.在△ABC中,∠A=40°,∠C=70°,则△ABC是 三角形.
13.等腰三角形一腰上的高与另一腰的夹角为60°,那么这个等腰三角形的底角为 .
14.在中,,点D为斜边上的一点,,若为等腰三角形,那么的度数为 .
15.如图,在△ABC中,∠A=58°,AB=AC,BD=CF,BE=CD,则∠EDF= 度.
16.如图,△ABC的两条角平分线相交于O,过O的直线MN∥BC交AB于M交AC于N,若BC=8cm,△AMN的周长是12cm,则△ABC的周长等于 cm.
17.如图,△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,且BD=BE,则∠ADE是 度.
18.在中,,点是外一点,连接、、,且交于点,在上取一点,使得,,若,则的度数为 .
三、解答题
19.如图,在中,,、是边上的点,且,求证:.
20.如图,中,,点D和E分别在边和上,,连接和.求证:.
21.如图,在四边形中,,,,垂足为点,.
(1)求证:.
(2)若,求的度数.
22.如图,在中,,,求的度数.
23.如图,中,,D为上一点,E为延长线上一点,且交于G.求证:.
24.如图,在中,,点、、分别在、、边上,且,.
(1)求证:为等腰三角形;
(2)当时,求的度数.
25.如图,在中,AD平分,过点B作AD的垂线,垂足为点D,,交AB于点E,.
(1)求证:是等腰三角形;
(2)求证:.
26.如图,点在线段上,点在线段上,,,,,分别是,的中点.
(1)求证AE=CD
(2)连接MN,判断△MBN的形状,并证明
27.在中,,,将一块足够大的直角三角尺PMN(,)按如图所示放置,顶点P在线段AB上滑动,三角尺的直角边PM始终经过点C,并且与CB的夹角,斜边PN交AC于点D.
(1)当时,______度.
(2)在点P滑动的过程中,当AP的长度为多少时,与全等?说明理由.
(3)在点P滑动的过程中,的形状可以是等腰三角形吗?若不可以,请说明理由;若可以,请求出的大小.
28.如图,在中,,,,,三点共线,点在上,,,分别交于,两点.
(1)求证:;
(2)若.
①求证:;
②探究,与的数量关系,并证明.
答案
一、单选题
1.D
【分析】分别从若腰长为3,底边长为6,若腰长为6,底边长为3,去分析求解即可求得答案,注意三角形的三边关系.
【解析】解:①若腰长为3,底边长为6,
∵3+3=6,
∴不能组成三角形,舍去;
②若腰长为6,底边长为3,
则它的周长是:6+6+3=15.
∴它的周长是15,
故选:D.
2.D
【分析】利用三线合一的性质对每一个选项进行验证从而求解.
【解析】解:∵△ABC中,AB=AC,D是BC中点,
∴∠B=∠C,(故A正确)
AD⊥BC,(故B正确)
∠BAD=∠CAD(故C正确)
无法得到AB=2BD,(故D不正确).
故选:D.
3.A
【分析】利用AD=AC,求出∠ADC=∠C=,利用AD=AB,即可求得∠B=∠BAD.
【解析】∵AD=AC,
∴∠ADC=∠C,
∵,
∴∠ADC=∠C=,
∵AD=AB,
∴∠B=∠BAD,
故选:A.
4.A
【分析】设另一个角是x,表示出一个角是2x-20°,然后分①x是顶角,2x-20°是底角,②x是底角,2x-20°是顶角,③x与2x-20°都是底角根据三角形的内角和等于180°与等腰三角形两底角相等列出方程求解即可.
【解析】设另一个角是x,表示出一个角是2x﹣20°,
①x是顶角,2x﹣20°是底角时,x+2(2x﹣20°)=180°,
解得x=44°,
所以,顶角是44°;
②x是底角,2x﹣20°是顶角时,2x+(2x﹣20°)=180°,
解得x=50°,
所以,顶角是2×50°﹣20°=80°;
③x与2x﹣20°都是底角时,x=2x﹣20°,
解得x=20°,
所以,顶角是180°﹣20°×2=140°;
综上所述,这个等腰三角形的顶角度数是44°或80°或140°.
故选:A.
5.B
【分析】判断三角形中是否有相等的角,以及根据定义,是否有相等的边即可判断.
【解析】A、∠C=180° 30° 60°=90°,没有相等的角,则不是等腰三角形,A选项错误;
B、∠C=180° 50° 80°=50°,有相等的角,则是等腰三角形,B选项正确;
C、∵∠A=2∠B=80°,
∴∠B=40°,
∴∠C=60°,没有相等的角,则不是等腰三角形,C选项错误;
D、∵AB=3,BC=6,周长为13,
∴AC=13 6 3=4,没有相等的边,则不是等腰三角形,D选项错误;
故答案选:B.
6.A
【分析】把变形得到可得三角形形状.
【解析】解:因为:,所以:,
所以:,所以三角形ABC是等腰三角形,
故选A.
7.C
【分析】设AB=AC=x,则BC=16-2x,根据三角形的三边关系即可求出AB的取值范围.
【解析】在等腰△ABC中,AB=AC,其周长为16cm,
设设AB=AC=cm,则BC=16-2x,
依题意得,
解得4cm<AB<8cm,
选C.
8.B
【分析】延长AD到G使得,连接BG,证明,根据全等三角形的性质可得到,AC=BD,等量代换得到BE=BG,再由等腰三角形的性质得到,推出EF=AF,即可解决问题;
【解析】如图,延长AD到G使得,连接BG,
∵AD是△ABC的中线,
∴CD=BD,
在△ACD与△GBD中,
,
∴,
∴,AC=BD,
∵BE=AC,
∴BE=BG,
∴,
∵,
∴,
∴EF=AF,
∴,
即,
∴;
故选:B.
9.D
【分析】由旋转的性质可得CA=CA',∠ACA'=α,由等腰三角形的性质可得∠A=∠CA'A=60°,由三角形内角和定理可求α的值.
【解析】解:,,
,
将绕点顺时针旋转角至△,
,,
,
,
,
故选:.
10.A
【分析】在边上取点,使,连接,得到,在边上取点,使,连接,得到,即可推出结论.
【解析】解:要想求的长,仅需知道和的长,理由是:
如图4,中,,,
,
∵BD平分,
,,
在边上取点,使,连接,
在和中,
,
,
,
,
在边上取点,使,连接,
则,
,,
,
,
,
,
.
故选:A.
二、填空题
11.7
【分析】根据等腰三角形底边上三线合一的性质进行分析即可.
【解析】解:等腰三角形的角平分线,中线、高彼此重合的只计一条,即底边上的高、中线、角平分线只计一条,因此总条数最多有7条,故答案为7
12.等腰
【分析】根据三角形的内角和定理求出∠B,即可判断.
【解析】解:∵在△ABC中,∠A=40°,∠C=70°,
∴∠B=180°-∠A-∠C=70°
∴∠B=∠C
∴△ABC为等腰三角形
故答案为:等腰.
13.或
【分析】首先根据题意画出图形,然后分别从锐角三角形与钝角三角形分析求解即可求得答案.
【解析】解:根据题意得:AB=AC,BD⊥AC,
如图(1),∠ABD=60°,
则∠A=30°,
∴∠ABC=∠C=75°;
如图(2),∠ABD=60°,
∴∠BAD=30°,
∴∠ABC=∠C=∠BAD=15°.
故这个等腰三角形的底角是:75°或15°.
故答案为:或.
14.55°或
【分析】根据直角三角形的两个锐角互余可得∠A+∠B=90°,然后根据等腰三角形腰的情况分类讨论,分别画出对应的图形,根据等边对等角和三角形的内角和定理即可分别求出结论.
【解析】解:∵在中,,
∴∠A+∠B=90°
当DA=DC时,如下图所示
∴∠A=∠ACD=35°
∴∠B=90°-∠A=55°;
当CA=CD时,如下图所示
∴∠A=∠CDA=(180°-∠ACD)=
∴∠B=90°-∠A=;
当AC=AD时,
∴∠ADC=∠ACD=35°
∴∠A=180°-∠ADC-∠ACD=110°,不符合实际,舍去;
综上:的度数为55°或
故答案为:55°或.
15.61°
【分析】先由等腰三角形的性质求得∠B的大小,再证明△EBD≌△DFC,得到∠DEB=∠FDC;又由三角形内角和为∠BED+∠B+∠EDB=180°,即∠FDC+∠B+∠EDB=180°,可得∠FDC+∠EDB=180°-∠B由因为∠BDC是平角可得:∠EDF=180°-(∠FDC+∠EDB),即可完成作答.
【解析】解:∵等腰三角形ABC
∴
在△EBD和△DFC中
∴△EBD≌△DFC(AAS)
∴∠DEB=∠FDC
又∵在△EBD中,∠BED+∠B+∠EDB=180
∴∠FDC+∠EDB=180°-∠B=119°
又∵∠EDF+(∠FDC+∠EDB)=180°
∴∠EDF=180°-(∠FDC+∠EDB)= 180°-119°=61°
故答案为61°.
16.20
【分析】由已知条件根据平行线的性质、角平分线的性质及等角对等边可得MO=MB,NO=NC.从而根据△AMN的周长求出AB+AC,问题得解.
【解析】解:∵BO平分∠ABC,
∴∠ABO=∠OBC.
又∵MN∥BC,
∴∠MOB=∠OBC.
∴∠ABO=∠MOB,
∴MO=MB.
同理可得:NO=NC.
∴△AMN的周长为:AM+MN+AN=AM+MO+ON+AN=AM+MB+NC+AN=AB+AC=12cm,
∴△ABC的周长为:AB+AC+BC=12+8=20cm.
故答案为20.
17.15
【分析】根据等腰三角形的性质得到∠B=∠C=30°,∠ADB=90°,根据三角形内角和定理计算.
【解析】∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵AB=AC,AD是BC边上的中线,
∴∠ADB=90°,
∵BD=BE,
∴∠BDE=75°,
∴∠ADE=15°,
故答案为15.
18.
【分析】根据证明,再利用全等三角形的性质,然后由三角形的外角性质,,可说明,再利用等腰三角形的性质可求出,最后利用三角形的内角和解答即可.
【解析】解:∵,
∴,
即,
在和中,
,
∴,
∴,
∵是和的外角,
∴,,
∴,
∴,
∵,,
∴,
∴,
∴.
故答案为:.
三、解答题
19.证明:∵,
∴,
在和中,
,
∴,
∴.
20.证明:,
∴,
在和中,
,
∴,
∴.
21.(1)证明:∵, ,
∴,,
∵,
∴∠AED=∠ABC=90°
∵,
∴;
(2)解:∵,
∴,,
∴∠ADC=∠ACD,
∴,
∵,
∴∠ADE+∠DAC=90°,
∴,
∴.
22.解:设,∵,∴,∵,∴,∴,∵,∴,在中,,,∴,解得,∴.
23.过点D作,交于F,
,
在与中
.
.
24.解:(1)∵,
∴,
在和中,
,
∴(),
∴,
∴为等腰三角形;
(2)∵,
∴,
∵是的外角,
∴,
∴,
∴,
在中,
∴,
∴.
25.(1)证明:如图,∵AD平分∠BAC,
∴∠1=∠2,
∵,CD∥AB,
∴.
∵,,
∴,
∴,
∴是等腰三角形;
(2)证明:由(1)得
∴,
∵,,,
∴,
∴,
∴.
26.(1)证明:(1)在和中,
,
∴.
∴AE=CD;
(2)是等腰直角三角形,理由如下:
连接MN,如图所示:
∵在(1)中已得,,
∴,,AE=DC,
∵M、N分别是AE、CD的中点,
∴,,
∴DN=AM,
又∵,,
∴,
∴BN=BM,,
∵,
∴,
∴是等腰直角三角形.
27.(1)解:当PNBC时,∠α=∠NPM=30°,
又∵∠ACB=120°,
∴∠ACP=120°﹣30°=90°,
故答案为:90;
(2)解:当AP=4时,△ADP≌△BPC,
理由为:∵∠ACB=120°,CA=CB,
∴∠A=∠B=30°,
又∵∠APC是△BPC的一个外角,
∴∠APC=∠B+∠α=30°+∠α,
∵∠APC=∠DPC+∠APD=30°+∠APD,
∴∠α=∠APD,
又∵AP=BC=4,
∴△ADP≌△BPC;
(3)解:的形状可以是等腰三角形.
由题意得,,
①当时,是等腰三角形,
∴,即,
∴.
②当时,是等腰三角形,
∴,
即,
∴.
③当时,是等腰三角形,
∴,
∴,
即,
∴,
此时点P与点B重合,点D和点A重合.
综上所述,当或90°或0°时,是等腰三角形.
28.(1)证明:,,
,
,
,
,
在与中,
,
;
(2)①证明:由(1)知,为等腰直角三角形,
,
,
,即,
,,
,
,
由(1)知,,
,
,
,
;
②,证明如下:
在上,取,连接,过点作交于点,
在与中,
,
,,,
,,三点共线,
,
,
为等腰直角三角形,即有,
,
,
,
,
,
,
,
,
,
在与中,
,
,
.
同课章节目录
