5.4平抛运动规律的应用 课件(共19张PPT)2025年高一下学期物理人教版(2019)必修第二册
文档属性
| 名称 | 5.4平抛运动规律的应用 课件(共19张PPT)2025年高一下学期物理人教版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 984.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-02-25 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
5.4专题:平抛运动规律及应用(斜面、曲面约束下的平抛)
2025年高一下学期物理人教版(2019)必修第二册
斜面约束的平抛运动
曲面约束的平抛运动
①物体从斜面上某一点抛出以后又重新落到斜面上,此时平抛运动物体的合位移方向与水平方向的夹角等于斜面的倾角。
一、斜面约束的平抛运动
常见模型:
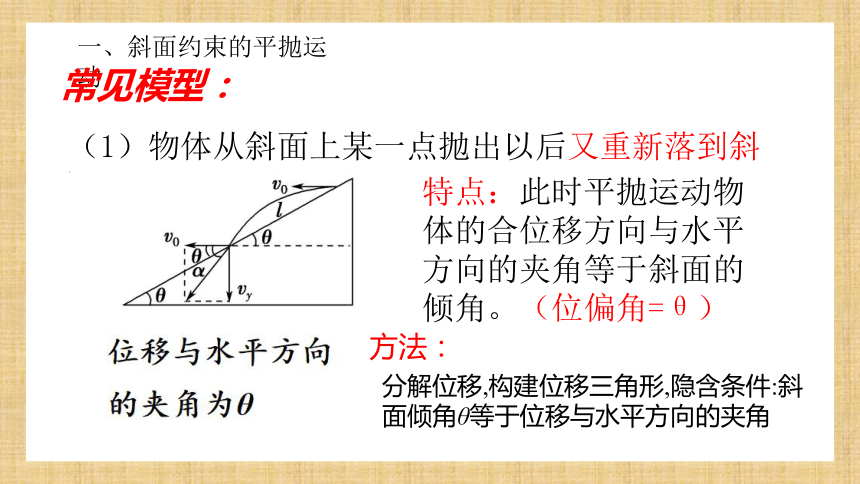
(1)物体从斜面上某一点抛出以后又重新落到斜面上。
特点:此时平抛运动物体的合位移方向与水平方向的夹角等于斜面的倾角。(位偏角=θ)
方法:
分解位移,构建位移三角形,隐含条件:斜面倾角θ等于位移与水平方向的夹角
方法:
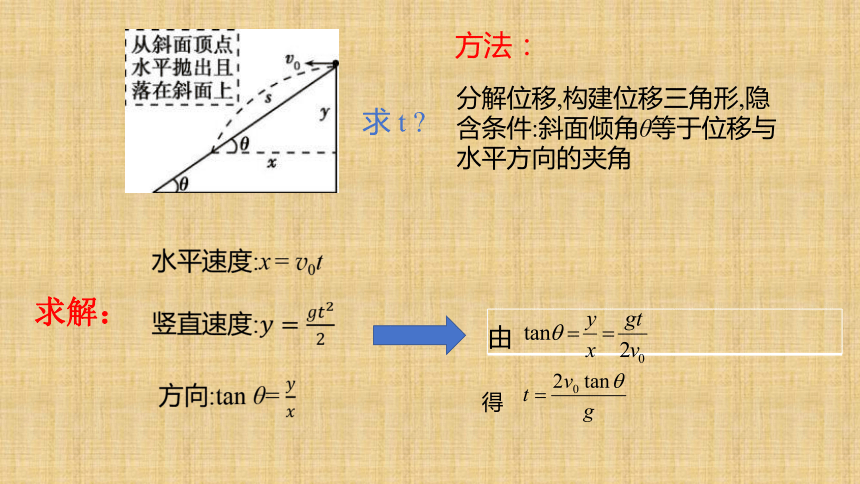
求解:
分解位移,构建位移三角形,隐含条件:斜面倾角θ等于位移与水平方向的夹角
由
水平速度:x = v0t
竖直速度:
方向:tan θ=
求 t
得
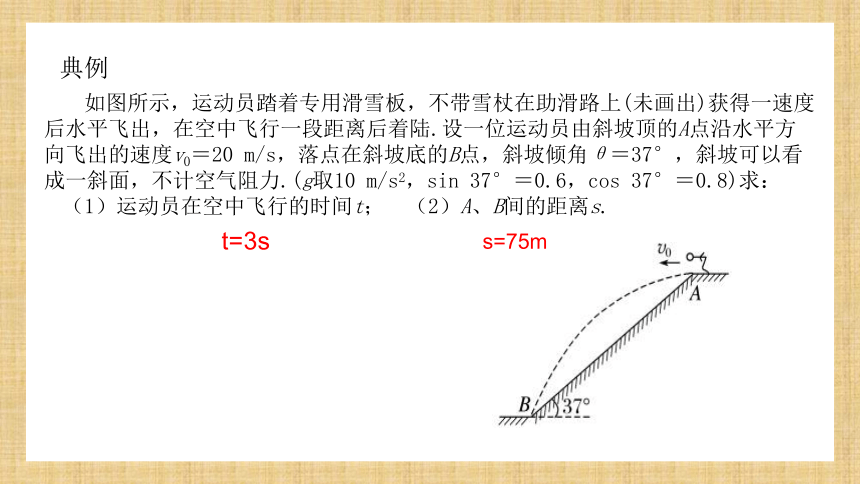
典例
如图所示,运动员踏着专用滑雪板,不带雪杖在助滑路上(未画出)获得一速度后水平飞出,在空中飞行一段距离后着陆.设一位运动员由斜坡顶的A点沿水平方向飞出的速度v0=20 m/s,落点在斜坡底的B点,斜坡倾角θ=37°,斜坡可以看成一斜面,不计空气阻力.(g取10 m/s2,sin 37°=0.6,cos 37°=0.8)求:
(1)运动员在空中飞行的时间t; (2)A、B间的距离s.
t=3s
s=75m
(2)垂直打在斜面上。
特点:此时物体的合速度方向与斜面垂直。(速偏角=90°-θ)
方法:
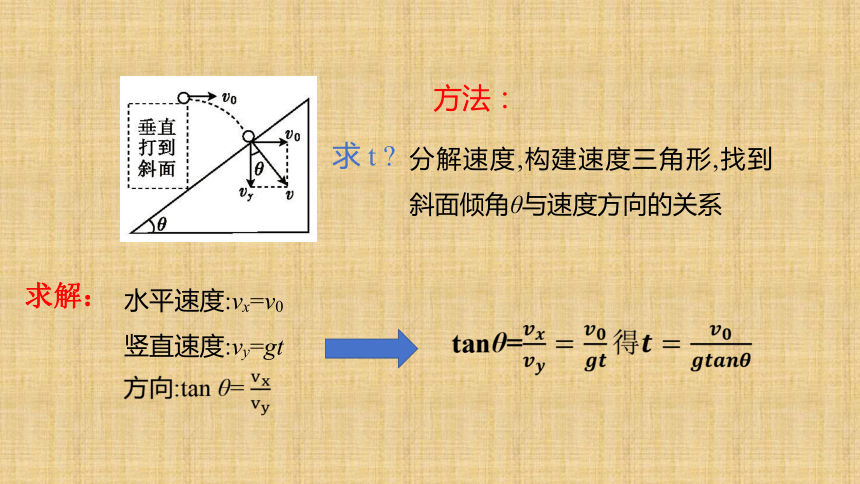
分解速度,构建速度三角形,找到斜面倾角θ与速度方向的关系
分解速度,构建速度三角形,找到斜面倾角θ与速度方向的关系
水平速度:vx=v0
竖直速度:vy=gt
方法:
方向:tan θ=
tanθ=
求解:
求 t
典例
如图所示,小球以15 m/s的水平初速度向一倾角为37°的斜面抛出,飞行一段时间后,恰好垂直撞在斜面上.(不计空气阻力,g取10 m/s2,sin 37°=0.6,cos 37°=0.8,tan 37°=3/4在这一过程中,求:
(1)小球在空中的飞行时间t;
(2)抛出点距撞击点的竖直高度h;
(3)小球撞到斜面时,小球在竖直方向上下落的距离与在水平方向上通过的距离之比是多少?
2s
20m
2:3
tanθ=
(3)物体恰好切入斜面的平抛运动
方法:
求解:
水平速度:vx=v0
竖直速度:vy=gt
由几何关系有:tan θ=
分解速度,构建速度的矢量三角形
求 t
典例:如图所示,一小物块从B点以10m/s的初速度做平抛运动,并恰好从C点以平行斜面方向的速度进入斜面,斜面倾角为45°,(g=10m/s2)求:小物块从B运动到C的时间?
解:竖直方向上, ①
恰好沿斜面方向进入斜面,则有
由①和②可得t=1s
(4)以最小位移到达斜面
方法:
求解:
分解位移,构建位移的矢量三角形
二、曲面约束的平抛运动
常见的两类模型:
(2)抛出点和落点都在圆面上。
如图所示,一小球从与圆心等高的半圆形轨道的A点以v0水平向右抛出,落在圆形轨道上的C点。
(1)球内平抛:若物体在球形空间内做平抛运动,需要考虑球的半径对物体运动轨迹的限制。比如,物体不能超出球的内部空间,这就要求在计算物体的位移和速度时,要保证其轨迹始终在球内,可能会涉及到利用勾股定理来判断物体位置与球心的距离是否小于球的半径等条件
典例:
如图所示,半球面半径为R,A点与球心O等高,小球两次从A点以不同的速率沿AO方向抛出,下落相同高度h,分别撞击到球面上B点和C点,速度偏转角分别为和,不计空气阻力。则小球( )
A.运动时间 B.两次运动速度变化
C.在C点的速度方向可能与球面垂直 D.
D
D
与曲面相关的平抛运动
(2)抛出点在圆面外,落点在圆面上。
如图所示,一小球从一半圆轨道左端A点正上方某处开始做平抛运动,飞行过程中恰好与半圆轨道相切于B点。
(2)圆周上平抛:当物体在圆周(如半圆形容器边缘)上某点做平抛运动时,要考虑物体在运动过程中与圆(球)的几何关系。例如,物体从半圆轨道边缘平抛,其运动轨迹与圆(球)可能会相切或者相交。在相切的临界情况下,通过圆心与切点的连线垂直于物体在该点的速度方向,结合平抛运动的速度规律可以求出临界初速度等参数。
典例
如图所示,一个半径R=0.75m的半圆柱体放在水平地面上,一小球从圆柱体左端A点正上方的B点水平抛出(小球可视为质点),恰好从半圆柱体的C点掠过。已知O为半圆柱体圆心,OC与水平方向夹角为53°,重力加速度为g=10 m/s2,求:
(1)B到C点所用时间;
(2)小球初速度;
5.4专题:平抛运动规律及应用(斜面、曲面约束下的平抛)
2025年高一下学期物理人教版(2019)必修第二册
斜面约束的平抛运动
曲面约束的平抛运动
①物体从斜面上某一点抛出以后又重新落到斜面上,此时平抛运动物体的合位移方向与水平方向的夹角等于斜面的倾角。
一、斜面约束的平抛运动
常见模型:
(1)物体从斜面上某一点抛出以后又重新落到斜面上。
特点:此时平抛运动物体的合位移方向与水平方向的夹角等于斜面的倾角。(位偏角=θ)
方法:
分解位移,构建位移三角形,隐含条件:斜面倾角θ等于位移与水平方向的夹角
方法:
求解:
分解位移,构建位移三角形,隐含条件:斜面倾角θ等于位移与水平方向的夹角
由
水平速度:x = v0t
竖直速度:
方向:tan θ=
求 t
得
典例
如图所示,运动员踏着专用滑雪板,不带雪杖在助滑路上(未画出)获得一速度后水平飞出,在空中飞行一段距离后着陆.设一位运动员由斜坡顶的A点沿水平方向飞出的速度v0=20 m/s,落点在斜坡底的B点,斜坡倾角θ=37°,斜坡可以看成一斜面,不计空气阻力.(g取10 m/s2,sin 37°=0.6,cos 37°=0.8)求:
(1)运动员在空中飞行的时间t; (2)A、B间的距离s.
t=3s
s=75m
(2)垂直打在斜面上。
特点:此时物体的合速度方向与斜面垂直。(速偏角=90°-θ)
方法:
分解速度,构建速度三角形,找到斜面倾角θ与速度方向的关系
分解速度,构建速度三角形,找到斜面倾角θ与速度方向的关系
水平速度:vx=v0
竖直速度:vy=gt
方法:
方向:tan θ=
tanθ=
求解:
求 t
典例
如图所示,小球以15 m/s的水平初速度向一倾角为37°的斜面抛出,飞行一段时间后,恰好垂直撞在斜面上.(不计空气阻力,g取10 m/s2,sin 37°=0.6,cos 37°=0.8,tan 37°=3/4在这一过程中,求:
(1)小球在空中的飞行时间t;
(2)抛出点距撞击点的竖直高度h;
(3)小球撞到斜面时,小球在竖直方向上下落的距离与在水平方向上通过的距离之比是多少?
2s
20m
2:3
tanθ=
(3)物体恰好切入斜面的平抛运动
方法:
求解:
水平速度:vx=v0
竖直速度:vy=gt
由几何关系有:tan θ=
分解速度,构建速度的矢量三角形
求 t
典例:如图所示,一小物块从B点以10m/s的初速度做平抛运动,并恰好从C点以平行斜面方向的速度进入斜面,斜面倾角为45°,(g=10m/s2)求:小物块从B运动到C的时间?
解:竖直方向上, ①
恰好沿斜面方向进入斜面,则有
由①和②可得t=1s
(4)以最小位移到达斜面
方法:
求解:
分解位移,构建位移的矢量三角形
二、曲面约束的平抛运动
常见的两类模型:
(2)抛出点和落点都在圆面上。
如图所示,一小球从与圆心等高的半圆形轨道的A点以v0水平向右抛出,落在圆形轨道上的C点。
(1)球内平抛:若物体在球形空间内做平抛运动,需要考虑球的半径对物体运动轨迹的限制。比如,物体不能超出球的内部空间,这就要求在计算物体的位移和速度时,要保证其轨迹始终在球内,可能会涉及到利用勾股定理来判断物体位置与球心的距离是否小于球的半径等条件
典例:
如图所示,半球面半径为R,A点与球心O等高,小球两次从A点以不同的速率沿AO方向抛出,下落相同高度h,分别撞击到球面上B点和C点,速度偏转角分别为和,不计空气阻力。则小球( )
A.运动时间 B.两次运动速度变化
C.在C点的速度方向可能与球面垂直 D.
D
D
与曲面相关的平抛运动
(2)抛出点在圆面外,落点在圆面上。
如图所示,一小球从一半圆轨道左端A点正上方某处开始做平抛运动,飞行过程中恰好与半圆轨道相切于B点。
(2)圆周上平抛:当物体在圆周(如半圆形容器边缘)上某点做平抛运动时,要考虑物体在运动过程中与圆(球)的几何关系。例如,物体从半圆轨道边缘平抛,其运动轨迹与圆(球)可能会相切或者相交。在相切的临界情况下,通过圆心与切点的连线垂直于物体在该点的速度方向,结合平抛运动的速度规律可以求出临界初速度等参数。
典例
如图所示,一个半径R=0.75m的半圆柱体放在水平地面上,一小球从圆柱体左端A点正上方的B点水平抛出(小球可视为质点),恰好从半圆柱体的C点掠过。已知O为半圆柱体圆心,OC与水平方向夹角为53°,重力加速度为g=10 m/s2,求:
(1)B到C点所用时间;
(2)小球初速度;
